Question: Q. 6. (i) Define electric flux. Write its S.I. unit.
(ii) A small metal sphere carrying charge $+Q$ is located at the centre of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure. Use Gauss’s law to find the expressions for the electric field at points $P_{1}$ and $P_{2}$.
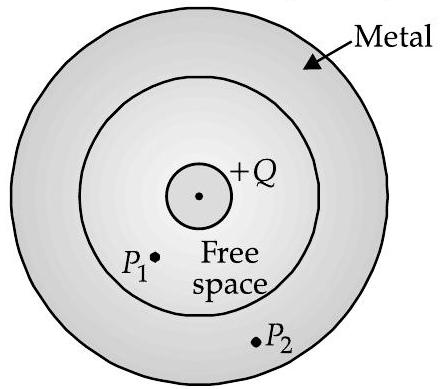
(iii) Draw the pattern of electric field lines in this arrangement. [Delhi, O.D. Comptt. I, II, III, 2012]
Show Answer
Solution:
Ans. (i) Try yourself, Similar to Q. 2, Very Short Answer Type Questions
(ii) Try yourself, Similar to Q. 12, Short Answer Type Questions-II (iii) The direction of electric field is shown in the figure.
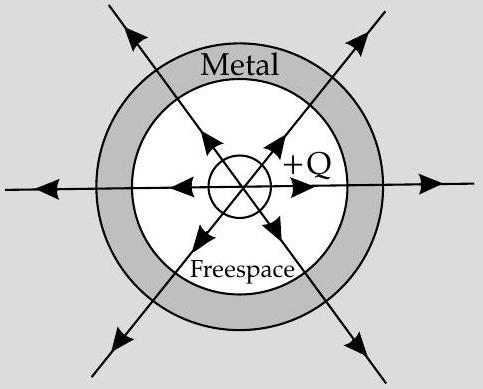
[CBSE Marking Scheme, 2012]
[IIQ.7.(i) An electric dipole of dipole moment $\vec{p}$ consists of point charges $+q$ and $-q$ separated by a distance $2 a$ apart. Deduce the expression for the electric field $\vec{E}$ due to the dipole at a distance $x$ from the centre of the dipole on its axial line in terms of the dipole moment $\vec{p}$. Hence show that in the limit $x»a, \vec{E} \rightarrow \frac{2 \vec{p}}{\left(4 \pi \varepsilon_{0} x^{3}\right)}$.
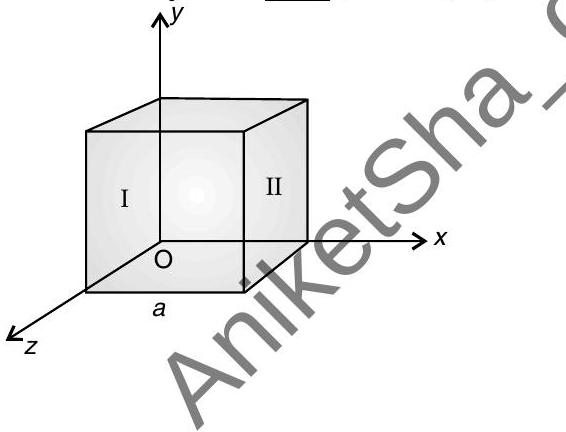
(ii) Given the electric field in the region $\vec{E}=2 x i$, find the net electric flux through the cube and the charge enclosed by it. R&U [Delhi I, II, III 2015]
Ans. (i)
Electric field intensity at point $P$ due to charge $-q$,
$$ \vec{E}{-q}=\frac{1}{4 \pi \varepsilon{0}} \cdot \frac{-q}{(x+a)^{2}}(\hat{x}) $$
Due to charge $+q$,
$$ \vec{E}{+q}=\frac{1}{4 \pi \varepsilon{0}} \cdot \frac{q}{(x-a)^{2}}(\hat{x}) $$
Net electric field at point $P$,
$$ \begin{aligned} & \vec{E}=\vec{E}{-q}+\vec{E}{+q}^{+q} \ & \vec{E}=\frac{q}{4 \pi \varepsilon_{0}} \times\left(\frac{1}{(x-a)^{2}}-\frac{1}{(x+a)^{2}}\right)(\hat{x}) 1 / 2 \end{aligned} $$
$$ \vec{E}=\frac{q}{4 \pi \varepsilon_{0}} \times\left(\frac{4 a q x}{\left(x^{2}-a^{2}\right)^{2}}\right)(\hat{x}) $$
$$ \begin{aligned} & =\frac{q}{4 \pi \varepsilon_{0}} \times \frac{(q \times 2 a) 2 x}{\left(x^{2}-a^{2}\right)^{2}}(\hat{x}) \ & =\frac{q}{4 \pi \varepsilon_{0}} \times \frac{2 p x}{\left(x^{2}-a^{2}\right)^{2}}(\hat{x}) \end{aligned} $$
$1 / 2$
FFor $x»a,\left(x^{2}-a^{2}\right)^{2} \simeq x^{4}$
$$ \vec{E}=\frac{q}{4 \pi \varepsilon_{0}} \times \frac{2 p}{x^{3}}(\hat{x})=\frac{1}{4 \pi \varepsilon_{0}} \frac{2 \vec{p}}{x^{3}} $$
(ii) From the given diagram,
Only the face perpendicular to the direction of $x$-axis, contribute to the electric flux. The remaining faces of the cube give zero contribution.
Total flux $\phi=\phi_{\mathrm{I}}+\phi_{\mathrm{II}}$
$$ \begin{array}{ll} =\oint_{\mathrm{I}} \vec{E} \cdot \overrightarrow{d s}+\oint_{\mathrm{II}} \vec{E} \cdot \overrightarrow{d s} & 1 / 2 \ =0+2(a) \cdot a^{2} & 1 / 2 \ =2 a^{3} & 1 / 2 \end{array} $$
Charge enclosed, $\quad q=\varepsilon_{0} \phi=2 a^{3} \varepsilon_{0}$
OSWAAL LEARNING TOOLS
For Suggested Online Videos
Or Scan the Code
