Question: Q. 12. Using Gauss’s law deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius at a point (i) outside, and (ii) inside the shell.
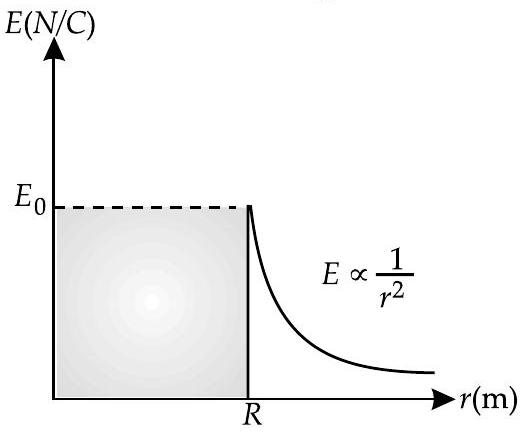
Plot a graph showing variation of electric field as function of and ( being the distance from the centre of the shell).
A [O.D. & O.D. Comptt. I, II, III, 2013;
Delhi I, II, III 2009]
Show Answer
Solution:
Ans. Electric field due to a uniformly charged thin spherical shell :
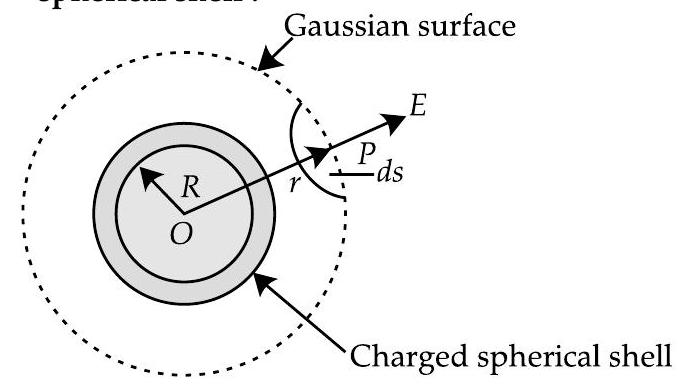
(i) When point lies outside the spherical shell : Suppose that we have to calculate electric field at the point at a distance from its centre. Draw the Gaussian surface through point so as to enclose the charged spherical shell. The Gaussian surface is a spherical shell of radius and centre . Let be the electric field at point , then the electric flux through area element is given by,
Since is also along normal to the surface,
Total electric flux through the Gaussian surface is given by.
Now,
Since the charge enclosed by the Gaussian surface is according to the Gauss’s law,
From equations (i) and (ii), we obtain
(ii) When point lies inside the spherical shell : In such a case, the Gaussian surface encloses no charge. According to the Gauss’s law,
A graph showing the variation of electric field as a function of is shown in figure.