Solution:

Ans. Statement of Gauss Law 1

Derivation of electric field due to infinitely long straight uniformly charged wire

The surface integral of electric field over a closed surface is equal to $\frac{1}{{\epsilon }_0}$ times the charge enclosed by the surface.

Alternatively,

$$\begin{array}{}\text{(1)}& \oint \overrightarrow{E}\cdot \overrightarrow{d}s=\frac{q}{{\epsilon }_0}\end{array}$$

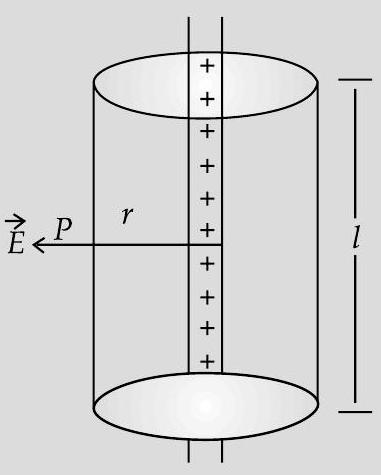
Flux through the Gaussian surface

$=$ flux through the curved cylindrical part of the surface

$=\mathrm{E}\times 2\pi rl$

$$1/2$$

Charge enclosed by the surface $=\frac{\lambda }{2\pi {\epsilon }_{0}r}$

$$=E\times (2\pi rl)$$

$$\begin{array}{rlr}& =\frac{\lambda l}{{\epsilon }_0}\mathrm{E}& =\frac{\lambda }{2\pi {\epsilon }_{0}r}\end{array}$$

[CBSE Marking Scheme, 2017]

Detailed Answer :

Gauss Law states that total electric flux over the closed surface $S$ will be $1/{\epsilon }_0$ times the total charge which is ${\varphi }_E=\oint Eds=\frac{q}{{\epsilon }_0}$

In a long straight wire with uniform charge per unit length $\lambda$, there should be electric field generated by charge distribution for cylindrical symmetry. Also, field to point will radially be away from the wire.

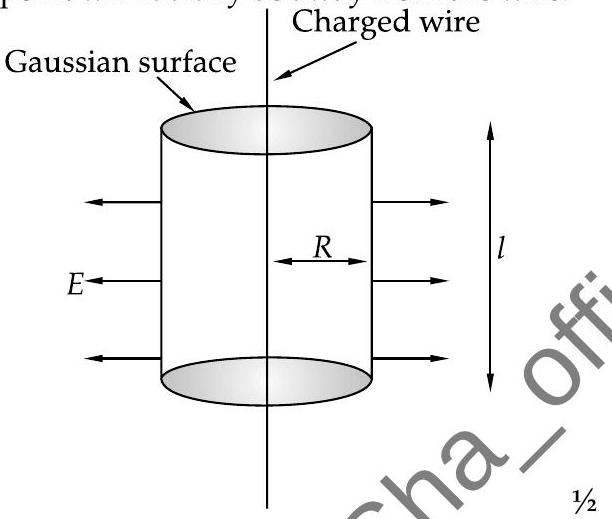
In this, cylindrical gaussian surface is co-axial with the wire of radius $R$ and length where symmetry implies to electric field generated by wire that will be perpendicular to curred-surface of cylinder, so as per Gauss’ law,

$$E(R)\times 2\pi Rl=\frac{\lambda l}{{\epsilon }_0}$$

where, $E(R)$ is electric field strength which acts at perpendicular distance $R$ from the wire.

In figure, left part shows electric flux through Gaussian surface while right part shows total charge enclosed by cylinder which is divided by ${\epsilon }_0$.

Further, $E(R)=\frac{\lambda }{2\pi {\epsilon }_{0}R}$

Here, the field points radially away from the wire when $\lambda >0$, and radially towards the wire when $\lambda <0$.

Commonly Made Error

• Some candidates do not know the correct expression. Few candidates are not sure about $\frac{1}{R}$ or $\frac{1}{R^2}$ (dependence of $E$ on $R$ ). AT Q. 4. A charge $Q$ is distributed uniformly over a metallic sphere of radius $R$. Obtain the expression for the electric field $(E)$ and electric potential $(V)$ at a point $0<x<R$.

Show or plot the variation of $E$ and $V$ with $x$ for $0<x<2R$. A&E [Foreign I, II, III 2017]

Ans. Expression for electric field

$1\frac{1}{2}$

Expression for potential

Plot of graph ( $E$ Vs $r$ ) $1/2$

Plot of graph $(VVsr)$

By Gauss law

$1/2$

$q=0$ in interval $0<x<\mathrm{R}$

$$E=0$$

or

$E=-\frac{dV}{dr}$

Hence, $V=$ constant $=V=\frac{1}{4\pi {\epsilon }_0}\cdot \frac{Q}{R}$

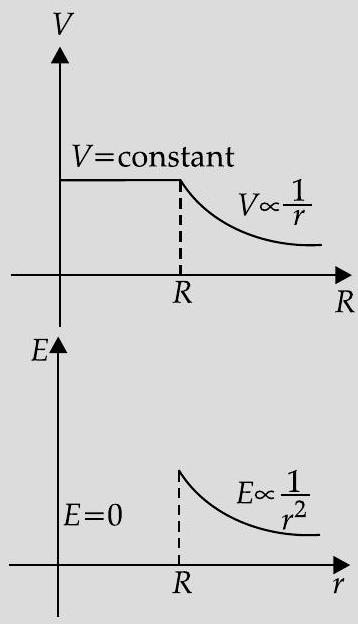
[Even if a student draws $E$ and $V$ for $0<r<R$ award $1/2+1/2$ mark]

[CBSE Marking Scheme, 2017]