SATHEE: electric-charges-and-fields Question 29

विद्युत आवेश और क्षेत्र

Question: Q. 2. (i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.

(ii) Two point charges $+ 4 μ C$ and $+ 1 μ C$ are separated by distance of $2 m$ in air. Find the point on the line joining charges at which the net electric field of the system is zero? U [O.D. (Comptt.) I, II, III 2017]

Show Answer

Solution:

Ans. (i) Derivation of expression for electric field.

(ii) Finding point on line joining charges 2

[CBSE Marking Scheme, 2017]

Detailed Answer :

(i) Try yourself, Similar to Q. 1 (i), Short Answer Type Questions-II.

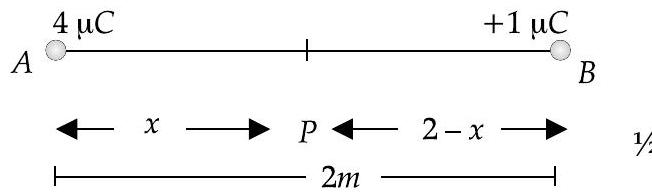
(ii) Two point charges $q_{A} = + 4 μ C$ and $q_{B} = + 1 μ C$ are located $2 m$ apart in air as shown. $P$ be a point, at a distance $x$ from $A$ , where electric field of the system is zero.

Distance between the two charges, $A B = 2 m$

$∴ PA = x m, PB = (2 - x) m$

Electric field at point $P$ caused by $+ 4 μ C$ charge,

$E_{1} = \frac{4 \times 10^{- 6}}{4 π ε_{0} (P A)^{2}} N / C along P A 1 / 2$

Magnitude of electric field at point $P$ caused by $+ 1 μ C$ charge

$E_{2} = \frac{+ 1 \times 10^{- 6}}{4 π ε_{0} (P B)^{2}} N / C$ along $P B$

Now, $\frac{4 \times 10^{- 6}}{4 π ε_{0} (x)^{2}} = \frac{+ 1 \times 10^{- 6}}{4 π ε_{0} (2 - x)^{2}}$

(Since net electric field at $P$ is zero) $1$ $(2 - x)^{2} 4 = (x)^{2} 1$

$16 - 16 x + 3 x^{2} = 0$

$4 (4 - x) - 3 x (4 - x) = 0$

$(4 - 3 x) (4 - x) = 0$

$x = \frac{4}{3}, x = 4$ , possible point on the line will be $x = \frac{4}{3} 1 / 2$

AI Q. 3. (a) Derive an expression for the electric field $E$ due to a dipole of length ’ $2 a^{'}$ at a point distant $r$ from the centre of the dipole on the axial line.

(b) Draw a graph of $E$ versus $r$ for $r » a$ .

(c) If this dipole were kept in a uniform external electric field $E_{0}$ , diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both the cases.

R [O.D. Set III 2017]

Ans. $n)$	$\overset{\vec{D}}{\to}$
	$- 1 - \leq - 10$
	$a a E - q$
	二.
$\infty$ (n)	$\overset{p}{\to}$
	$- 1 - 1 - 10$
	$i$ a $+ q E - q$
	$∴ 1 - x - 1$
	Considee a depole haverig depole momenc
	P. Ececteic fceld due to $- q$ at the pocnt $P$ is along $p Q$ .
	$E = 1 q$ along $P B$
	$- q 4 π ε_{0} (γ + a)^{2}$
	Fectsid fceld due to tq at the pocnl $P$
	$∴$ along $P A$ ?
	$E_{t a} = \frac{1}{4 π ε_{0}} \frac{q}{(γ - a)^{2}} a long p A$