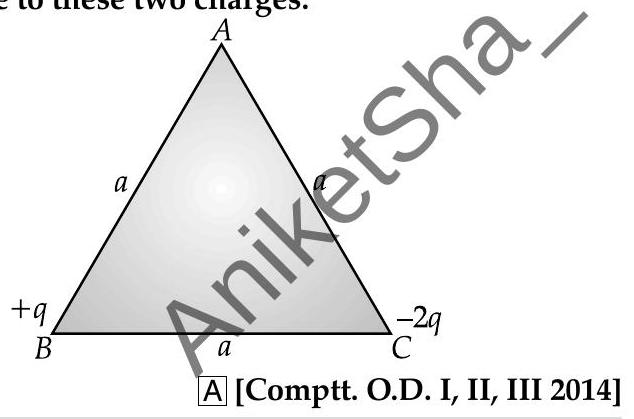
Question: Q. 6. Two point charges and are placed at the vertices ’ ’ and ’ ’ of an equilateral triangle of side ’ ’ as given in the figure. Obtain the expression for (i) the magnitude and (ii) the direction of the resultant electric field at the vertex A due to these two charges.
Show Answer
Solution:
Ans. (i) The magnitude
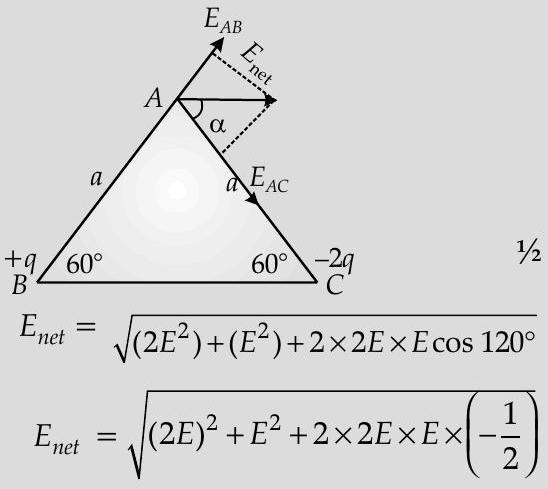
(ii) The direction of resultant electric field at vertex
[CBSE Marking Scheme, 2014]
[AT Q. 7. A charge is distributed uniformly over a ring of radius ’ ‘. Obtain an expression for the electric intensity at a point on the axis of the ring. Hence, show that for points at large distances from the ring, it behaves like a point charge.
A [Delhi I, II, III, 2016]
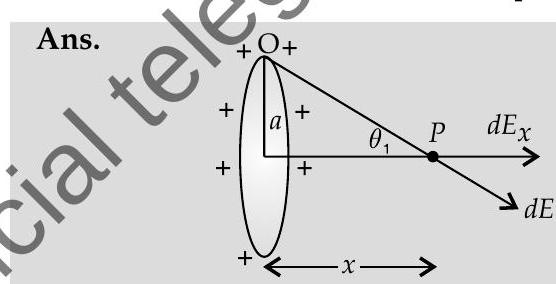
, by Pythagoras theorem
where, is radius of ring
is the distance from centre to point ’ '
and will be zero because all components will cancel out each other.
Now, if
, which is equal to field produced by a point change.
For large distance, ring behaves as a point charge. 1
[CBSE Marking Scheme, 2016]









