Question: Q. 5. Two thin concentric and coplanar spherical shells, of radii $a$ and $b(b>a)$ carry charges, $q$ and $Q$, respectively. Find the magnitude of the electric field, at a point at distance $x$, from their common centre for :
(i) $0<x<a$
(ii) $a \leq x<b$
(iii) $b \leq x<\infty$
A [Comptt. Delhi, 2016]
Show Answer
Solution:
Ans.
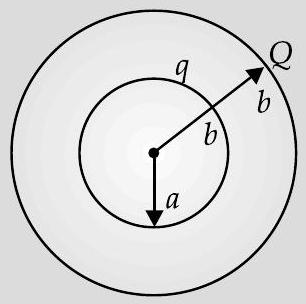
(i) For $0<x<a$
Point lies inside both the spherical shells. Hence, $E(x)=0$
(ii) For $a \leq x<b$
Point is outside the spherical shell of radius ’ $a$ ’ but inside the spherical shell of radius ’ $b$ ‘.
$$ \therefore E(x)=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{x^{2}} $$
1
(iii) For $b \leq x \leq \infty$
Point is outside of both the spherical shells. Total effective charge at the centre equals $(Q+q)$.
$$ \begin{equation*} \therefore E(x)=\frac{1}{4 \pi \varepsilon_{0}} \cdot\left(\frac{q+\mathrm{Q}}{x^{2}}\right) \tag{1} \end{equation*} $$
[CBSE Marking Scheme, 2016]
