SATHEE: electric-charges-and-fields Question 19

विद्युत आवेश और क्षेत्र

Question: Q. 9. A particle of mass $10^{- 3} kg$ and charge $5 μ C$ enters into a uniform electric field of $2 \times 10^{5} {NC}^{- 1}$ , moving with a velocity of $20 {ms}^{- 1}$ in a direction opposite to that of the field. Calculate the distance it would travel before coming to rest.

A [Delhi Comptt. I, II, III, 2012]

Show Answer

Solution:

Ans. Here, $m = 10^{- 3} kg, q = 5 \times 10^{- 6} C, E = 2 \times 10^{5} N / C$ , $u = 20 m / s, v = 0$

As the particle enters opposite to the field, so it will retard.

Acceleration

$\begin{aligned} a & = - \frac{q E}{m} & = - \frac{5 \times 10^{- 6} \times 2 \times 10^{5}}{10^{- 3}} \end{aligned}$

$= - 10^{3} m / s^{2}$

Using,

$v^{2} = u^{2} - 2 a s$

$0 = (20)^{2} - 2 \times 1000 \times s$

$\Rightarrow s = \frac{400}{2000} = \frac{1}{5} = 0.2 m$

[CBSE Marking Scheme, 2012]

Unstable equilibrium $θ = 180^{\circ}$

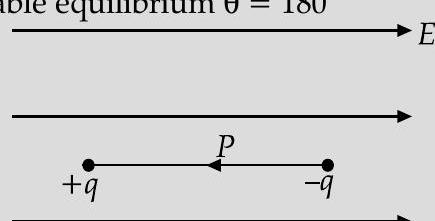
[CBSE Marking Scheme, 2017]

(AI) Q. 2. (i) Obtain the expression for the torque $\vec{τ}$ experienced by an electric dipole of dipole moment $\vec{p}$ in a uniform electric field, $\vec{E}$ .

(ii) What will happen if the field were not uniform?

R [Delhi III 2017]

Ans. (i) Obtaining expression for torque $\vec{τ}$ experienced by electric dipole in uniform electric field 2

(ii) Effect of non-uniform electric field

(i) Force on $+ q, \vec{F} = q \vec{E}$

Force on $- q, \vec{F} = - q \vec{E}$

Magnitude of torque $\vec{τ} = q E \times 2 a \sin θ$

$= 2 q a E \sin θ$

$\vec{τ} = \vec{p} \times \vec{E}$

(ii) If the electric field is non-uniform, the dipole experiences a translatory force as well as a torque.

[CBSE Marking Scheme, 2017]

Detailed Answer :

(i)

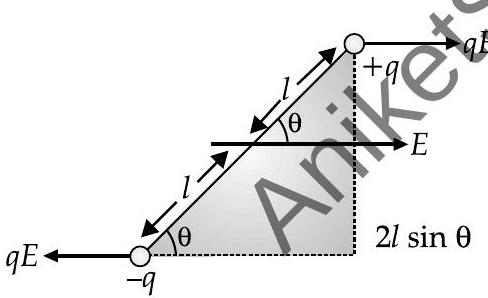
Consider electric dipole kept in an uniform electric field at an angle $θ$ where a dipole experience a torque, so, torque generated by parallel forces $q E$ will act as couple as

$\begin{aligned} | \vec{τ} | & = q E 2 l \sin θ & = p E \sin θ [as p = 2 q l] 1 / 2 | \vec{τ} | & = | \vec{p} \times \vec{E} | \end{aligned}$

(ii) When the field is non-uniform, force acting on both ends will not be equal, hence they result in mixture of couple and net force. With this, dipole experiences rotational as well as linear force. $1$

विद्युत आवेश और क्षेत्र

Detailed Answer :

विषयसूची

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

विद्युत आवेश और क्षेत्र

Detailed Answer :

विषयसूची

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu