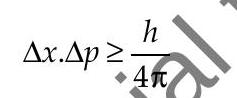Question: Q. 1. (i) Write three observed features of photoelectric effect which cannot be explained by wave theory of light.
Explain how Einstein’s photoelectric equation is used to describe these features satisfactorily.
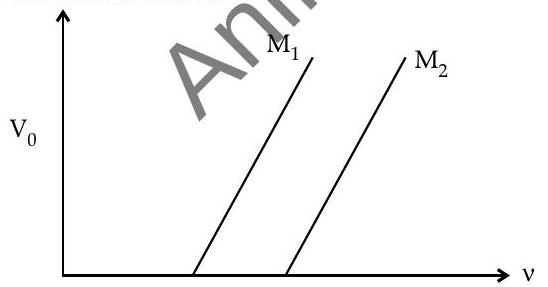
(ii) Figure shows a plot of stopping potential $\left(V_{0}\right)$ with frequency $(v)$ of incident radiation for two photosensitive materials $M_{1}$ and $M_{2}$. Explain
(a) Why the slope of both the lines is same?
(b) For which material emitted electrons have greater kinetic energy for the same frequency of incident radiation?
U [O.D. I, II, III 2015]
Show Answer
Solution:
Ans. (i) Three features of photoelectric effect, which cannot be explained by the wave theory of light, are :
(a) Maximum kinetic energy of emitted electrons is independent of the intensity of incident light.
(b) There exists a ’threshold frequency’ for each photosensitive material. (c) ‘Photoelectric effect’ is instantaneous in nature.
Einstein’s photoelectric equation
$$ K . E_{{ }{\max }}=h v-\phi{0} $$
[Alternatively : $e \mathrm{~V}{0}=h \nu-\phi{0}$ ] can be used to explain these features as follows.
(a) Einstein’s equation shows that $K_{\max } \propto v$. However, $K_{\max }$ does not depend on the intensity of light.
(b) Einstein’s equation shows that for $v<\frac{\phi_{0}}{h}, K_{\max }$ becomes negative, i.e, there cannot be any photoemission for $v<v_{0}\left(\right.$ where, $\left.v_{0}=\frac{\phi_{0}}{h}\right)$.
(c) The free electrons in the metal, that absorb completely the energy of the incident photons, get emitted instantaneously.
(ii) (a) Slope of the graph between $\mathrm{V}_{0}$ and $v$ (from Einstein’s equation) equals $(h / e)$. Hence it does not depend on the nature of the material.
(b) Emitted electrons have greater energy for material $\mathrm{M}{1}$. This is because $\phi{0}\left(=h v_{0}\right)$ has a lower value for material $M_{1}$.
[CBSE Marking Scheme 2015]
TOPIC-2
Revision Notes
de-Broglie’s postulate is based upon the symmetry of nature. If radiation has dual nature then matter should also have dual nature.
- According to his hypothesis, moving particles of matter should display wave nature under suitable conditions. He named this wave as matter wave. It is a third type of wave. It is different from mechanical wave and electromagnetic wave.
- Properties of matter wave : Whenever a particle moves, the matter wave envelops it and controls its motion.
- de-Broglie proposed that the wave length $\lambda$ known as de-Broglie wavelength; associated with momentum of particle $p$ is given as
$$ \lambda=\frac{h}{p} $$
Hence, de-Broglie’s wavelength of particle
$$ \lambda=\frac{h}{m v} $$
- Calculation of electron-wave :
In photoelectric equation, kinetic energy of electron at potential $V$ is $K=e V$. Putting this value of kinetic energy in de-Broglie wavelength equation
$$ \lambda_{e}=\frac{h}{\sqrt{2 m e V}} $$
By putting the value of mass of electron, its charge and Plancks’ constant $\lambda_{e}=\frac{1.227}{\sqrt{V}} \mathrm{~nm}$. This is theoretical calculation of de-Broglie wavelength of electron, where, $V$ is the magnitude of accelerating potential in volts.
- From this formula, wavelength of particle is inversely proportional to the mass of particle and its velocity. Hence, heavier particles have shorter wavelengths.
Heisenberg’s Principle of uncertainty
- According to Heisenberg’s uncertainty principle, it is not possible to measure both the position and momentum of an electron (or any other particle) at the same time exactly. When any particle is in motion then product of uncertainty of its momentum and uncertainty of its position is given as
$$ \Delta x \cdot \Delta p \geq \frac{h}{4 \pi} $$
- According to Heisenberg’s hypothesis, electron is not moving in an orbit but it is moving in a wave packet cloud.
Davisson and Germer’s Experiment : Davisson and Germer did the experiment to see the diffraction pattern for electron waves and verified for first time the wave nature of electron.
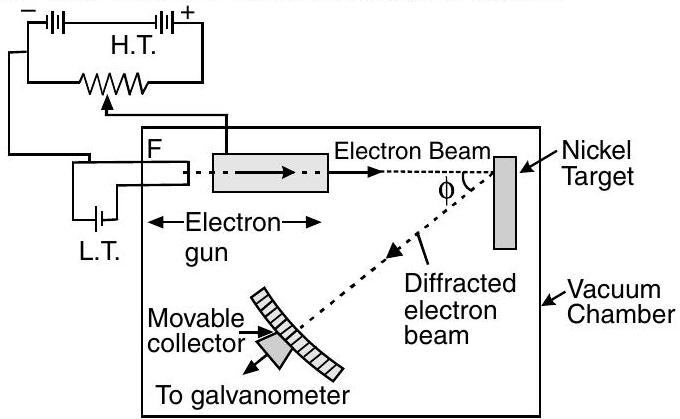
In their diffraction experimental setup, interatomic space between Nickel is taken as single slit. Scattered electron beams are collected by movable collector and its intensity is plotted in a radial graph.
In radial graph we take the observations at different angles and plot the graph.
The experiment was performed by varying the accelerating voltage from $44 \mathrm{~V}$ to $68 \mathrm{~V}$.
A strong peak appeared in the intensity $(I)$ of the scattered electron for an accelerating voltage of $54 \mathrm{~V}$ at a scattering angle $\theta=50^{\circ}$
The contrast of concentration of scattered electrons proved that electrons are moving in waveform and superposition of their wave appear as contrast of concentration of scattered electrons.
- Calculation of electron wavelength by wave optics diffraction formula and putting experimental values as for $1^{\text {st }}$ dark diffraction angle $50^{\circ}$ and interatomic space of nickel $d=0.91 \AA$ gives $\lambda=0.165 \mathrm{~nm}$.
Theoretical calculation of electron wavelength by de-Broglie formula $\left(\lambda_{e}=\frac{1.227}{\sqrt{V}} \mathrm{~nm}\right)$ by putting electrical potential value $V=54$ volts gives electron wavelength as $0.167 \mathrm{~nm}$.
This excellent agreement between theoretical and experimental value of electron wavelength confirms the wave nature of electrons and the de-Broglie relation.
The wave properties of electrons have been utilized in the design of electron microscope which have very high resolution, than the optical microscope.
Know the Formulae
De Broglie wavelength associated with momentum of particle $p$ as
$$ \lambda=\frac{h}{p} \text { or } \lambda=\frac{h}{m v} $$
$\lambda_{e}=\frac{h}{\sqrt{2 m e V}}$ or $\lambda_{e}=\frac{1.227}{\sqrt{V}}$ where $V$ is the magnitude of accelerating potential in Volts.
Heisenberg’s Principle of uncertainty :
