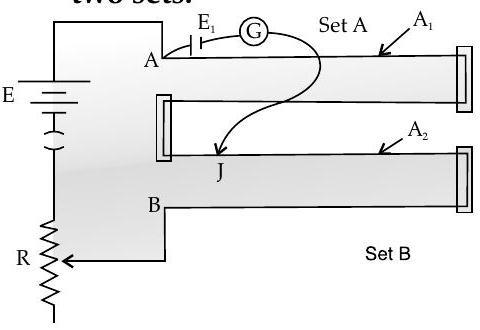
Question: Q. 12. You are given two sets of potentiometer circuit to measure the emf $E_{1}$ of a cell.
Set A : consists of a potentiometer wire of a material of resistivity $\rho_{1}$, area of cross-section $A_{1}$ and length $l$.
Set B : consists of a potentiometer of two composite wires of equal lengths $l_{2}$ each, of resistivity $\rho_{1}, \rho_{2}$ and area of cross-section $A_{1}, A_{2}$ respectively.
(i) Find the relation between resistivity of the two wires with respect to their area of cross section, if the current flowing in the two sets is same.
(ii) Compare the balancing length obtained in the two sets.
Show Answer
Solution:
Ans. (i)
$$ I=\frac{E}{R+\frac{\rho_{1} l}{A_{1}}} $$
$(\text { for } \operatorname{Set} A)^{1 / 2}$
$$ \mathrm{I}=\frac{E}{R+\frac{\rho_{1} l}{2 A_{1}}+\frac{\rho_{2} l}{2 A_{2}}} \quad(\text { for Set } B)^{1 / 2} $$
Equating the above two expressions and simplifying
$$ \frac{\rho_{1}}{A_{1}}=\frac{\rho_{2}}{A_{2}} $$
(ii) Potential gradient of the potentiometer wire for Set
$$ \text { A, } \quad K=I \frac{\rho_{1}}{A_{1}} $$
Potential drop across the potentiometer wire in Set $B$
$$ \begin{aligned} & V=\mathrm{I}\left(\frac{\rho_{1} l}{2 A_{1}}+\frac{\rho_{2} l}{2 A_{2}}\right) \ & V=\frac{I}{2}\left(\frac{\rho_{1}}{A_{1}}+\frac{\rho_{2}}{A_{2}}\right) l \ & K^{\prime}=\frac{I}{2}\left(\frac{\rho_{1}}{A_{1}}+\frac{\rho_{2}}{A_{2}}\right) \text {, using the condition obtained } \ & \text { in part (i) } 1 / 2 \ & K^{\prime}=I \frac{\rho_{1}}{A_{1}} \text {, which is equal to } K \end{aligned} $$
Therefore, balancing lengths obtained in the two sets are same.
