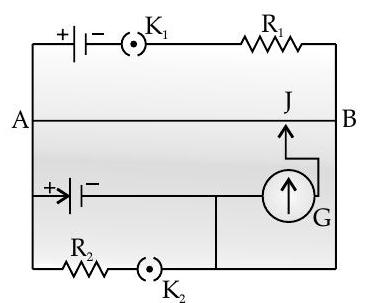
Question: Q. 1. For the circuit shown here, would the balancing length increase, decrease or remain the same, if
(i)
(ii)
without any other change, (in each case) in the rest of the circuit. Justify your answers in each case.
[C [CBSE SQP 2013]
Show Answer
Solution:
Ans. (i) Decreases
(The potential gradient would increase.)
(ii) Increases
(The terminal p.d. across the cell would increase.)
[CBSE Marking Scheme 2013]
Detailed Answer :
(i) If resistance
(ii) If resistance
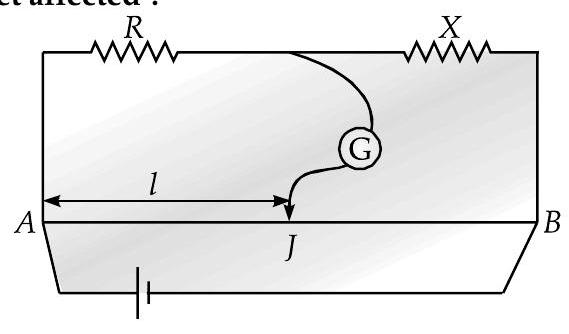
(AI Q. 2. In the metre bridge experiment, balance point was observed at
(i) The values of
(ii) If the galvanometer and battery are interchanged at the balance position, how will the balance point get affected ?
U [O.D. I, 2011; OD Comptt. I, II, III 2012]
Ans. (i)
[Note : even if the student does not mention the formula, award 1 mark
(ii) No change in the position of balance point. 1
[CBSE Marking Scheme, 2011, 12]
Detailed Answer :
(i) Using the formula to obtain balance point:
If
Hence, the new balance point position will be :
(ii) If the galvanometer and the battery gets interchanged, there will be no effect on the position of balance point since in null position; there will be no flow of current in the circuit.
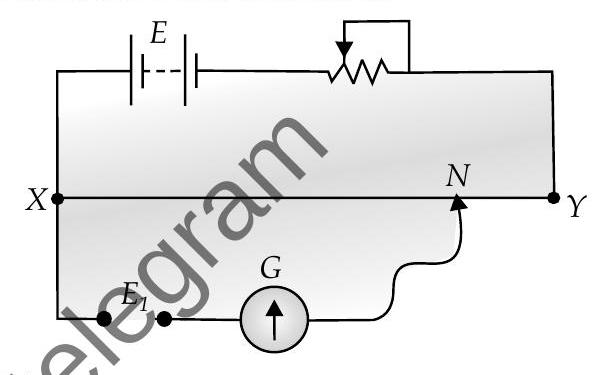
[A] Q. 3. The diagram below shows a potentiometer set up. On touching the jockey near to the end
A&E [CBSE S.Q.P. 2018-19]
S01. The positive of
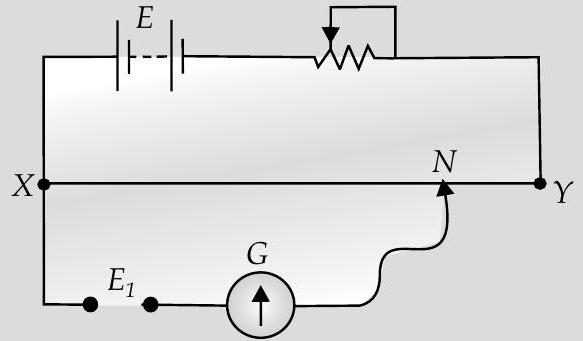
In loop PGJX,
So,
[CBSE Marking Scheme 2018]






