Question: Q. 7. The galvanometer, in each of the two given circuits, does not show any deflection. Find the ratio of the resistors 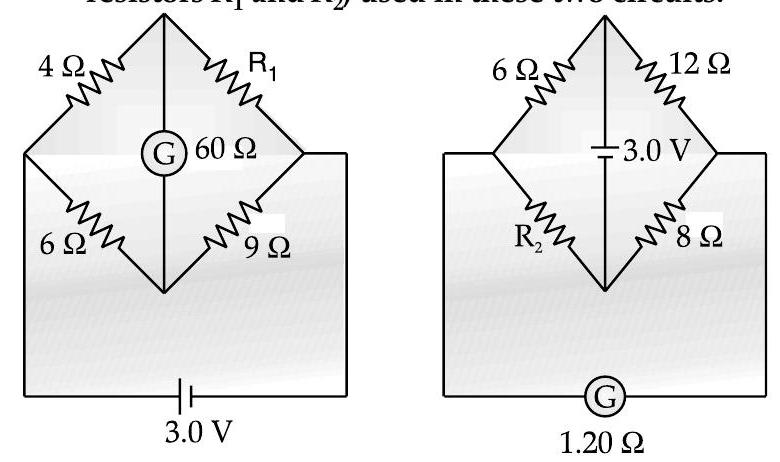
A [CBSE SQP 2013]
Show Answer
Solution:
Ans. For circuit 1, we have, (from the Wheatstone bridge balance condition),
In circuit 2, the interchange of the positions of the battery and the galvanometer, does not change the (Wheatstone Bridge) balance condition.
[AI Q. 8. Calculate the value of the resistance
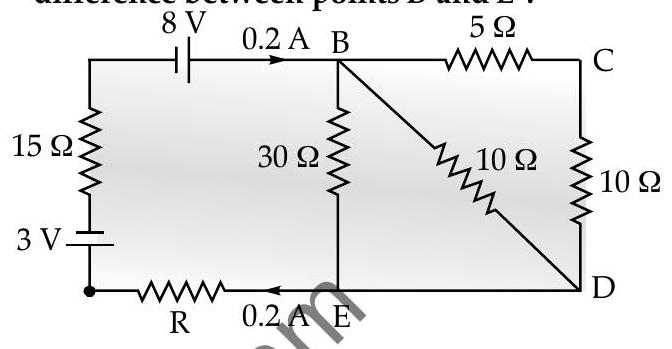
A [O.D. I, II, III 2012]
Ans.
Long Answer Type Questions
[AI Q. 1. (i) State the two Kirchhoff’s laws. Explain briefly how these rules are justified.
(ii) The current is drawn from a cell of emf
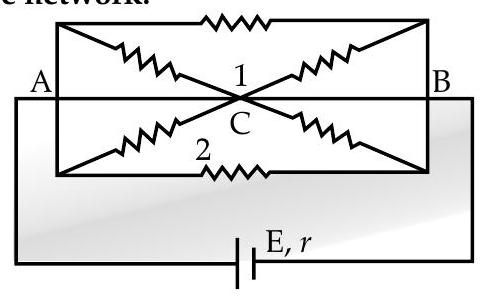
R [Delhi Compt I, II, III 2017]
Ans. (i) Try yourself Similar to Q. 1, Short Answer Type Question-I
(ii) Equivalent resistance of the loop
[CBSE Marking Scheme, 2012]
Hence current drawn from the cell
Power consumed,
Further since both mesh 1 and 2 are similar,
Now combining resistances
(As
1
As the circuit is in series with internal resistance, then resultant resistance will be :
Hence the current drawn from the cell will be :
Now power consumed by the network :






