Question: Q. 4. Two metallic wires $P_{1}$ and $P_{2}$ of the same material and same length but different cross-sectional areas $A_{1}$ and $A_{2}$ are joined together and then connected to a source of emf. Find the ratio of the drift velocities of free electrons in the wires $P_{1}$ and $P_{2}$, if the wires are connected (i) in series, and (ii) in parallel.
U] [Foreign II 2017]
Show Answer
Solution:
Ans. Ratio of drift velocities in series 1
Ratio of drift velocities in parallel
In series, the current remains the same
$$ \begin{array}{rlrl} I & =n e A_{1} v_{d_{1}}=n e A_{2} v_{d_{2}} \ \therefore & \frac{v_{d 1}}{v_{d 2}} & =\frac{A_{2}}{A_{1}} \end{array} $$
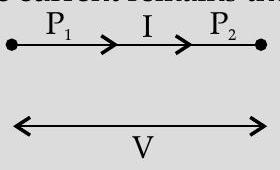
In parallel potential difference is same but currents are different.
$$ \begin{array}{ll} I_{1} R_{1}=I_{2} R_{2} \ \therefore \quad \frac{v_{d 1}}{v_{d 2}}=1 \end{array} $$
$$ \begin{aligned} V & =I_{1} R_{1} \ & =n e A_{1} v d_{1} \frac{\rho l}{A_{1}} \ & =n e \rho v_{d 1} l \ V & =I_{2} R_{2}=n e \rho v_{d 2} l \ R_{1} & =I_{2} R_{2} \ \frac{11}{12} & =1 \end{aligned} $$
[CBSE Marking Scheme 2017]
