Question: Q. 19. A $10 \mathrm{~V}$ battery of negligible internal resistance is connected across a $200 \mathrm{~V}$ battery and a resistance of $38 \Omega$ as shown in the figure. Find the value of the current in the circuit.
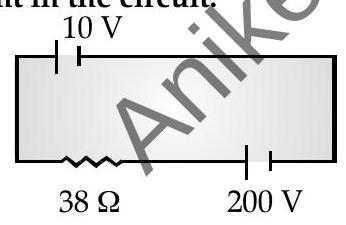
U] [Delhi I, II, III 2013, 2018]
Show Answer
Solution:
Ans. From the circuit we see that, the two batteries are joined together with positive terminal, so equivalent emf of both the batteries will result as :
$$ \begin{equation*} I=\frac{E}{R}=\frac{190}{38}=5 \mathrm{~A} \tag{1} \end{equation*} $$
[CBSE Marking Scheme 2013, 2018]
Alternatively :
$$ \begin{aligned} E_{\text {net }} & =E_{1}-E_{2} \ & =(200-10)=190 \mathrm{~V} \end{aligned} $$
Current in circuit, $I=\frac{E_{\text {net }}}{R}$
$$ =\frac{190}{38}=5 \mathrm{~A} $$
AI Q. 20. Two identical cells, each of emf $E$, having negligible internal resistance, are connected in parallel with each other across an external resistance $R$. What is the current through this resistance?
R [O.D. I, II, III 2013]
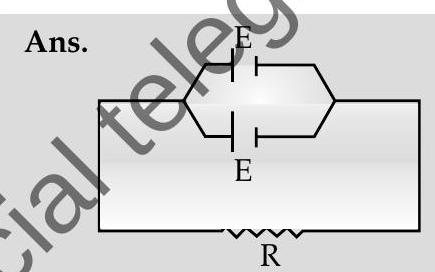
Since internal resistance is negligible, so total resistance $=R$
Potential difference across the resistance $=E$.
Hence, current through the resistance in the circuit :
$$ I=\frac{E}{R} $$
1
[CBSE Marking Scheme 2013]
