Question: Q. 1. (i) Distinguish between sinusoidal and pulseshaped signals.
(ii) Explain, showing graphically, how a sinusoidal carrier wave is superimposed on a modulating signal to obtain the resultant amplitude modulated (AM) wave.
U] [O.D. Comptt. I, II, III 2012; O.D. I, II, III 2014]
Show Answer
Solution:
Ans. (i)
| Sinusoidal signal (analog signal) |
Pulse signal (Digital signal) |
|---|---|
| (a) It is a continuous signal value, which at any instant lies within the range, of a maximum and minimum value. |
(a) These signals are those which can only take discrete stepwise values such a signal is usually in form of pulses. |
| (b) Sine wave is a fundamental analog signal |
(b) Each pulse have two levels of current of voltage represented by 0 and 1 . |
| (c) It is represented as | (c) It is represented graphi- cally as |
(ii) Amplitude Modulation : When a wave is superimposed on a high frequency carrier wave in a manner that the frequency of modulated wave is same as that of the carrier wave, but its amplitude is made proportional to the instantaneous amplitude of the audio frequency modulating voltage, the process is called amplitude modulation (AM).
Let the instantaneous carrier voltage
Thus, in amplitude modulation, amplitude A of modulated wave is made proportional to the instantaneous modulating voltage
i.e.,
where,
In amplitude modulation, the proportionality constant
It is called top envelope.
The maximum negative amplitude of AM wave is given by
This is called bottom envelope.
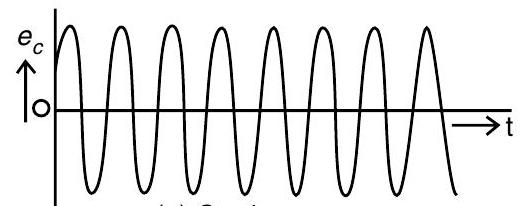
(a) Carrier wave
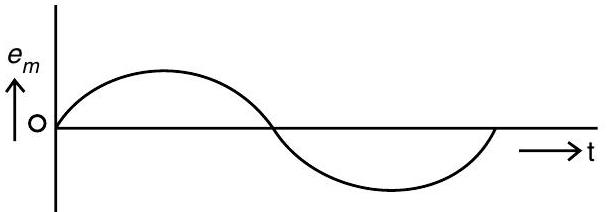
(b) Modulating Signal
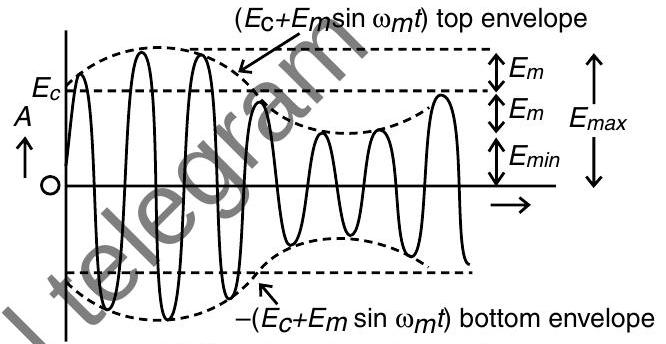
(c) Amplitude modulated wave
(a) Describe briefly three factors which justify the need for modulation of audio frequency signals over long distances in communication. (b) Draw the waveforms of (i) carrier wave, (ii) a modulating signal and (iii) amplitude modulated wave.
[CBSE Comptt- 2018]
Ans. (a) Describing the three factor 3
(b) Drawing the wave forms
2
(a) It is necessary to modulate the audio frequency signals because of the following three reasons :
(i) Size of the antenna or aerial
(ii) Effective power readiated
Power radiated, being proportional to
(iii) Mixing up of different signals
The audible frequency range is quite small. Hence if transformation is done at audio frequencies, the chances of mixing up of different signals are very high.
(b) The required wave forms are as shown
(i) Carrier wave
(ii) Modulating Signal
(iii) Amplitude Modulated wave
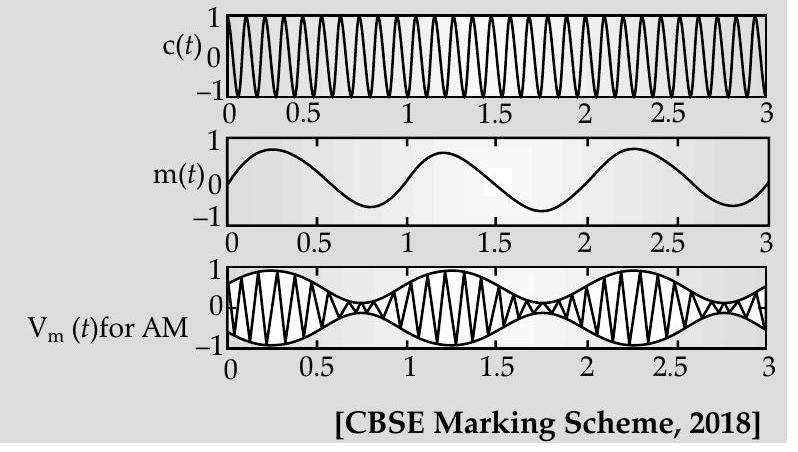
Detailed Answer :
(a) For a long distance Transmission of message signal we need modulation because of following reasons.
(i) Low energy: The message signals when converted to e.m. waves, do not have the sufficient energy to travel up to long distance, because of their low frequency. Hence these message signals are modulated with high frequency carrier signals before being send because carrier signals have high energy for long distance transmission.
(ii) Size of Antenna: For the effective Transmission by an antenna , the size of antenna should be at least of the size






