Question: Q. 1. (i) In Rutherford scattering experiment, draw the trajectory traced by
(ii) Describe briefly how wave nature of moving electrons was established experimentally.
(iii) Estimate the ratio of de-Broglie wavelengths associated with deuterons and
Show Answer
Solution:
Ans. (i) The trajectory, traced by the
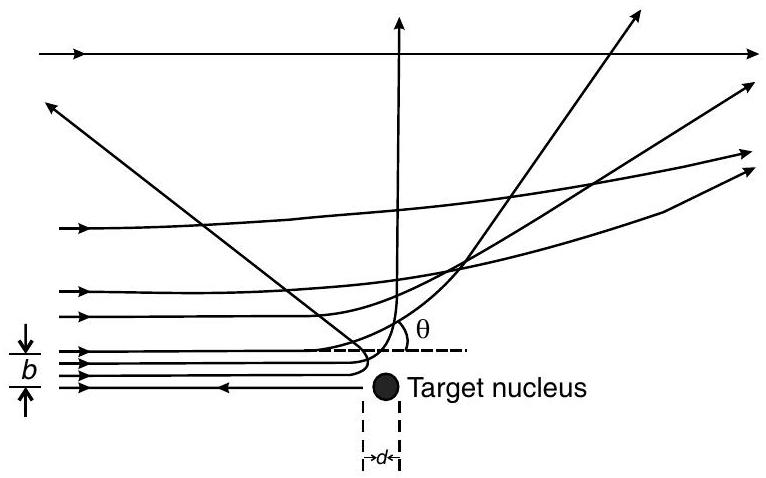
The size of the nucleus was estimated by observing the distance
where,
(ii) The wave nature of moving electrons was established through the Davisson-Germer experiment.
In this experiment, it was observed that a beam of electrons, when scattered by a nickel target, showed ‘maxima’ in certain directions; (like the ‘maxima observed in interference/diffraction experinents with light.)






