Question: Q. 3. (i) State Bohr’s quantization condition for defining stationary orbits. How does de-Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between the three wavelengths $\lambda_{1}, \lambda_{2}$ and $\lambda_{3}$ from the energy level diagram shown below.
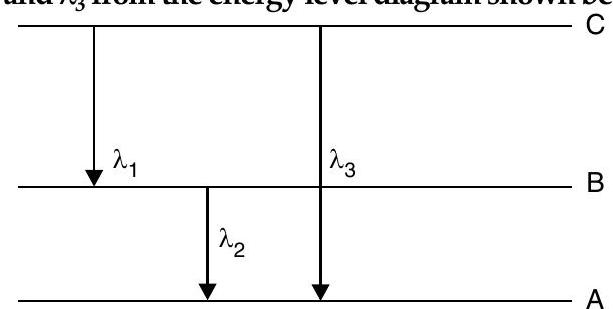
R [Delhi I, II, III 2016]
Show Answer
Solution:
Ans. (i) $L=\frac{n h}{2 \pi}$ i.e., angular momentum of orbiting electron is quantised.]
According to de-Broglie hypothesis
$1 / 2$
Linear momentum
$$ p=\frac{h}{\lambda} $$
And for circular orbit, $L=r_{n} p$ where ’ $r_{n}$ ’ is the radius of $n^{\text {th }}$ orbit
$$ =\frac{r_{n} h}{\lambda} $$
Also
$$ \mathrm{L}=\frac{n h}{2 \pi} $$
$\therefore \quad \frac{r_{n}}{\lambda}=\frac{n h}{2 \pi}$
$\Rightarrow$ $2 \pi r=n \lambda$ $1 / 2$
$\therefore$ Circumference of permitted orbits are integral multiples of the wave-length $\lambda$.
(ii)
$$ \begin{align*} & E_{C}-E_{B}=\frac{h c}{\lambda_{1}} \tag{i}\ & E_{B}-E_{A}=\frac{h c}{\lambda_{2}} \tag{ii}\ & E_{C}-E_{A}=\frac{h c}{\lambda_{3}} \tag{iii} \end{align*} $$
Adding (i) & (ii)
$$ \begin{equation*} E_{C}-E_{A}=\frac{h c}{\lambda_{1}}+\frac{h c}{\lambda_{2}} \tag{iv} \end{equation*} $$
Using equation (iii) and (iv)
$$ \begin{aligned} \frac{h c}{\lambda_{3}} & =\frac{h c}{\lambda_{1}}+\frac{h c}{\lambda_{2}} \ \Rightarrow \quad \frac{1}{\lambda_{3}} & =\frac{1}{\lambda_{1}}+\frac{1}{\lambda_{2}} \end{aligned} $$
[CBSE Marking Scheme 2016]
Commonly Made Error
- Many students couldn’t understand how to start. They had written the formulae of ‘Balmer, Lyman & Paschen Series.
