Question: Q. 14. The figure shows a series $L C R$ circuit with $L=$ $5.0 \mathrm{H}, C=80 \mu \mathrm{F}, R=40 \Omega$ connected to a variable frequency of $240 \mathrm{~V}$ source. Calculate
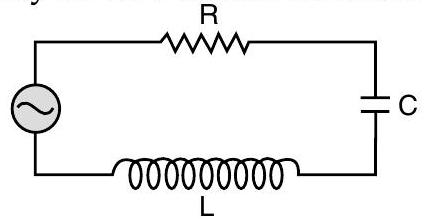
(i) The angular frequency of the source which drives the circuit at resonance.
(ii) The current at the resonating frequency.
(iii) The rms potential drop across the capacitor at resonance.
A [Delhi I, II, III 2012]
Show Answer
Solution:
Ans. (i)
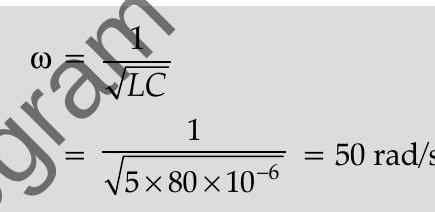
(ii) Current at resonance
$$ I_{r m s}=\frac{V_{r m s}}{R}=\frac{240}{40} \mathrm{~A}=6 \mathrm{~A} \quad 1 / 2+1 / 2 $$
(iii) $V_{r m s}$ across a capacitor
$$ \begin{aligned} V_{r m s} & =I_{r m s} X_{C} \ & =6 \times \frac{1}{50 \times 80 \times 10^{-6}} \mathrm{~V} \ & =\frac{6 \times 10^{6}}{4 \times 10^{3}} \mathrm{~V}=\frac{6000}{4} \mathrm{~V}=1500 \mathrm{~V} 1 / 2 \end{aligned} $$
[CBSE Marking Scheme, 2012]
