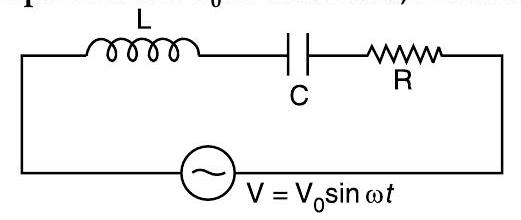
Question: Q. 7. The current, in the $L C R$ circuit shown in the figure is observed to lead the voltage in phase. Without making any other change in the circuit, a capacitor, of capacitance $C_{0}$, is (appropriately) joined to the capacitor $C$. This results in making the current, in the ‘modified’ circuit, flow in phase with the applied voltage.
Draw a diagram of the ‘modified’ circuit and obtain an expression for $C_{0}$ in terms of $\omega, L$ and $C$.
] [Foreign 2016]
Show Answer
Solution:
Ans. The current leads the voltage in phase. Hence, $X_{c}>X_{L}$
For resonance, we must have
$1 / 2$
New value of $\quad X_{c}=X_{L}$
We, therefore, need to decrease $X_{c}=\left(\frac{1}{\omega C}\right)$. This requires an increase in the value of $C$. Hence, capacitor $C_{0}$ should be connected in parallel across C. $1 / 2$ The diagram of the modified circuit is as shown.
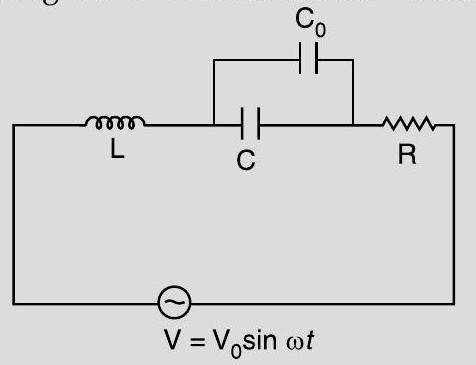
For resonance, we have
$$ \begin{align*} \frac{1}{\omega\left(C+C_{0}\right)} & =\omega L \ C_{0} & =\left[\frac{1}{\omega^{2} L}-C\right] \end{align*} $$
[CBSE Marking Scheme 2016]
