Question: Q. 4. The figure shows a series $L C R$ circuit connected to a variable frequency of $200 \mathrm{~V}$ source with $L=50 \mathrm{mH}, C=80 \mu \mathrm{F}$ and $R=40 \Omega$ find.
(i) the source frequency which drives the circuit in resonance;
(ii) the quality factor $(Q)$ of the circuit.
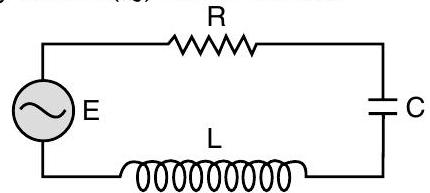
A [O.D. Comptt. I, II, III 2014]
Show Answer
Solution:
Ans. (i) $\quad \omega_{0}=\frac{1}{\sqrt{L C}}$
$\omega_{0}=\frac{1}{\sqrt{50 \times 10^{-3} \times 80 \times 10^{-6}}}=500 \mathrm{rad} / \mathrm{s}$
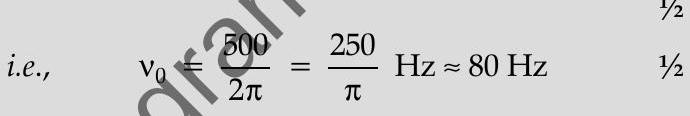
(ii)
[CBSE Marking Scheme 2014]
Short Answer Type Questions-II
[AI Q. 1. A source of $a c$ voltage $V=V_{0} \sin \omega t$, is connected across a pure inductor of inductance $L$. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
[Foreign I, II, III 2017]
Ans. Derivation of instantanteous current Derivation of average power dissipated
Given :$$ V=V_{0} \sin \omega t $$
$$ V=L \frac{d i}{d t} \Rightarrow d i=\frac{V}{L} d t $$
$$ \begin{aligned} & \therefore \quad d i=\frac{V_{0}}{L} \sin \omega t d t \ & \text { Integrating, } \quad i=-\frac{V_{0}}{\omega L} \cos \omega t \ & \therefore i=-\frac{V_{0}}{\omega L} \sin \left(\frac{\pi}{2}-\omega t\right)=I_{0} \sin \left(\frac{\pi}{2}-\omega t\right) \end{aligned} $$
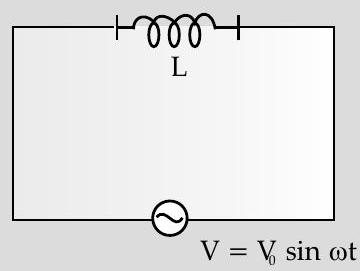
where,
$$ I_{0}=\frac{V_{0}}{\omega L} $$
Average power,
$$ \begin{align*} P_{a v} & =\int_{0}^{T} V i d t \ & =\frac{-V_{0}^{2}}{\omega L} \int_{0}^{T} \sin \omega t \cos \omega t d t \ & =\frac{-V_{0}^{2}}{2 \omega L} \int_{0}^{T} \sin (2 \omega \mathrm{t}) d t \ & =0 \tag{1} \end{align*} $$
[CBSE Marking Scheme 2017]
