Question: Q. 3. The power factor of an $a c$ circuit is 0.5 . What is the phase difference between voltage and current in the circuit?
A [O.D. I, 2016]
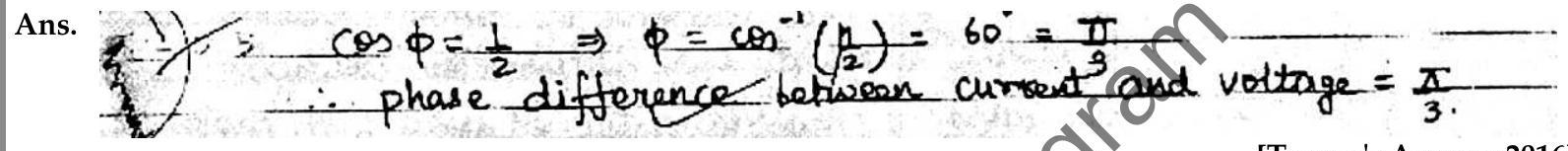
[Topper’s Answer 2016]
Short Answer Type Questions-1
(2 marks each)
Q. 1. An alternating voltage $E=E_{0} \sin \omega t$ is applied to the circuit containing a resistor $R$ connected in series with a black box. The current in the circuit is found to be $I=I_{0} \sin \left(\omega t+\frac{\pi}{4}\right)$
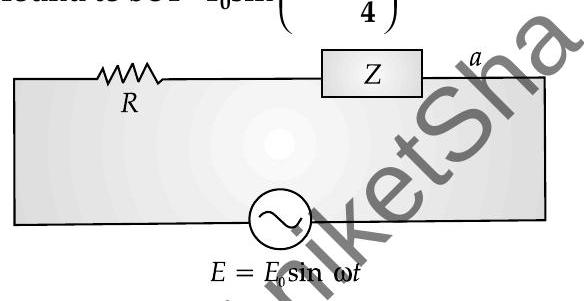
(i) State whether the element in the black box is a capacitor or inductor.
(ii) Draw the corresponding phasor diagram and find the impedance in terms of $R$.
U[ [CBSE SQP 2017-18]
Show Answer
Solution:
Ans. (i) As the current leads the voltage by $\frac{\pi}{4}$, the element used in black box is a ‘capacitor’.
(ii) Phasor diagram :
$$ \tan \frac{\pi}{4}=\frac{V_{C}}{V_{R}} $$
$$ \begin{align*} V_{C} & =V_{R} \ X_{C} & =R \ Z & =\sqrt{\left(X_{C}^{2}+R^{2}\right)} \ Z & =R \sqrt{2} \end{align*} $$
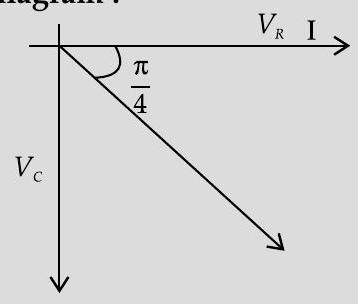
Impedance,
[CBSE Marking Scheme 2017]
[AI $Q$. 2. In a series $L C R$ circuit, obtain the conditions under which (i) the impedance of the circuit is minimum, and (ii) wattless current flows in the circuit.
U] [Foreign 2014]
Ans. (i) The impedance of a series $L C R$ circuit is given by
$Z=\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}$
$1 / 2$
or For $Z$ to be minimum, $X_{L}=X_{C}\left(\right.$ or $\left.\omega=\frac{1}{\sqrt{L C}}\right) 1 / 2$
(ii) For wattless current to flow, circuit should not have any ohmic resistance, i.e. $R=0$.
Alternatively, Power $=V_{r m s} I_{r m s} \cos \phi$
for
$$ \phi=90^{\circ}=\frac{\pi}{2} $$
$$ \text { Power }=0 $$
$\therefore$ Wattless current flows when the impedance of the circuit is purely inductive/capacitive or the combination of the two.
1
[CBSE Marking Scheme 2014]
