Triangles
7.1 Introduction
You have studied about triangles and their various properties in your earlier classes. You know that a closed figure formed by three intersecting lines is called a triangle. (‘Tri’ means ’three’). A triangle has three sides, three angles and three vertices. For example, in triangle
7.2 Congruence of Triangles

Fig. 7.1
You must have observed that two copies of your photographs of the same size are identical. Similarly, two bangles of the same size, two ATM cards issued by the same bank are identical. You may recall that on placing a one rupee coin on another minted in the same year, they cover each other completely.
Do you remember what such figures are called? Indeed they are called congruent figures (‘congruent’ means equal in all respects or figures whose shapes and sizes are both the same).
Now, draw two circles of the same radius and place one on the other. What do you observe? They cover each other completely and we call them as congruent circles.
Repeat this activity by placing one square on the other with sides of the same measure (see Fig. 7.2) or by placing two equilateral triangles of equal sides on each other. You will observe that the squares are congruent to each other and so are the equilateral triangles.

Fig. 7.2
You may wonder why we are studying congruence. You all must have seen the ice tray in your refrigerator. Observe that the moulds for making ice are all congruent. The cast used for moulding in the tray also has congruent depressions (may be all are rectangular or all circular or all triangular). So, whenever identical objects have to be produced, the concept of congruence is used in making the cast.
Sometimes, you may find it difficult to replace the refill in your pen by a new one and this is so when the new refill is not of the same size as the one you want to remove. Obviously, if the two refills are identical or congruent, the new refill fits.
So, you can find numerous examples where congruence of objects is applied in daily life situations.
Can you think of some more examples of congruent figures?
Now, which of the following figures are not congruent to the square in Fig 7.3 (i) :

Fig. 7.3
The large squares in Fig. 7.3 (ii) and (iii) are obviously not congruent to the one in Fig 7.3 (i), but the square in Fig 7.3 (iv) is congruent to the one given in Fig 7.3 (i).
Let us now discuss the congruence of two triangles.
You already know that two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.
Now, which of the triangles given below are congruent to triangle

Fig. 7.4
Cut out each of these triangles from Fig. 7.4 (ii) to (v) and turn them around and try to cover
If
Notice that when
That is,
Note that under this correspondence,
Similarly, for Fig. 7.4 (iii),
So,
Give the correspondence between the triangle in Fig. 7.4 (iv) and
So, it is necessary to write the correspondence of vertices correctly for writing of congruence of triangles in symbolic form.
Note that in congruent triangles corresponding parts are equal and we write in short ’
7.3 Criteria for Congruence of Triangles
In earlier classes, you have learnt four criteria for congruence of triangles. Let us recall them.
Draw two triangles with one side

Fig. 7.5
Now, draw two triangles with one side

Fig. 7.6
See that these two triangles are not congruent.
Repeat this activity with some more pairs of triangles.
So, equality of one pair of sides or one pair of sides and one pair of angles is not sufficient to give us congruent triangles.
What would happen if the other pair of arms (sides) of the equal angles are also equal?
In Fig 7.7,
Recall from your earlier classes that, in this case, the two triangles are congruent. Verify this for
Repeat this activity with other pairs of triangles. Do you observe that the equality of two sides and the included angle is enough for the congruence of triangles? Yes, it is enough.

Fig. 7.7
This is the first criterion for congruence of triangles.
Axiom 7.1 (SAS congruence rule) : Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
This result cannot be proved with the help of previously known results and so it is accepted true as an axiom (see Appendix 1).
Let us now take some examples.
Example 1 : In Fig. 7.8,
(i)
(ii)
Solution : (i) You may observe that in

Fig. 7.8
Also, since
So,
(ii) In congruent triangles
So,
Therefore,
Example 2 : AB is a line segment and line
Solution : Line
We have
So,
and so,

Fig. 7.9
Now, let us construct two triangles, whose sides are 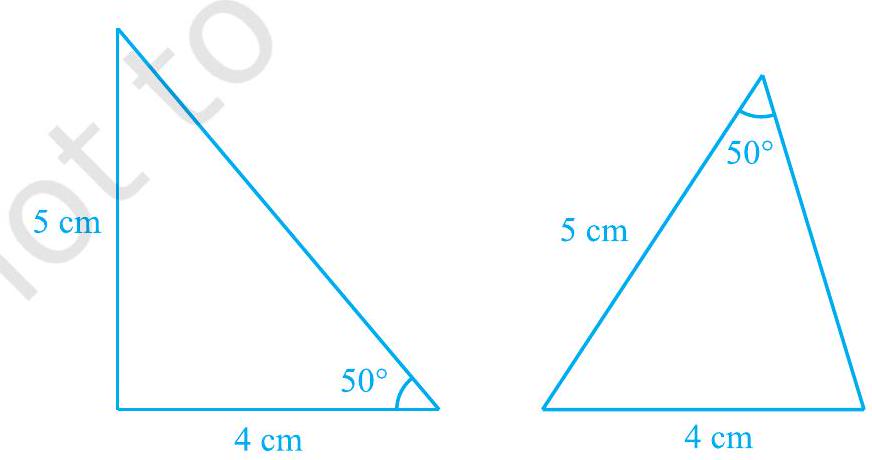
Fig. 7.10
Notice that the two triangles are not congruent.
Repeat this activity with more pairs of triangles. You will observe that for triangles to be congruent, it is very important that the equal angles are included between the pairs of equal sides.
So, SAS congruence rule holds but not ASS or SSA rule.
Next, try to construct the two triangles in which two angles are 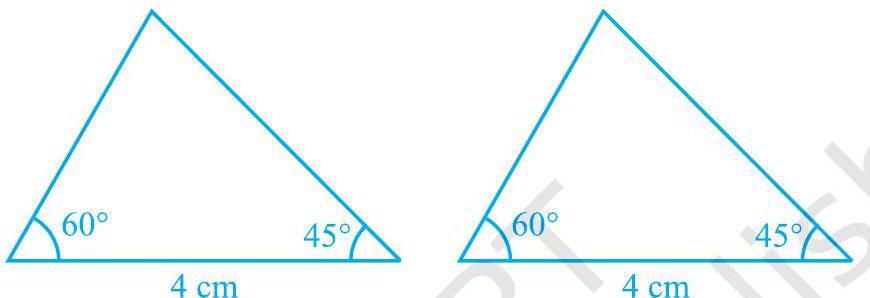
Fig. 7.11
Cut out these triangles and place one triangle on the other. What do you observe? See that one triangle covers the other completely; that is, the two triangles are congruent. Repeat this activity with more pairs of triangles. You will observe that equality of two angles and the included side is sufficient for congruence of triangles.
This result is the Angle-Side-Angle criterion for congruence and is written as ASA criterion. You have verified this criterion in earlier classes, but let us state and prove this result.
Since this result can be proved, it is called a theorem and to prove it, we use the SAS axiom for congruence.
Theorem 7.1 (ASA congruence rule) : Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
Proof : We are given two triangles
and
We need to prove that
For proving the congruence of the two triangles see that three cases arise.
Case (i) : Let
Now what do you observe? You may observe that
So,
Fig. 7.12
Case (ii) : Let if possible 
Fig. 7.13
Observe that in
So, we can conclude that:
Since the triangles are congruent, their corresponding parts will be equal.
So,
But, we are given that
So,
Is this possible?
This is possible only if
or,
So,
Case (iii) : If
Suppose, now in two triangles two pairs of angles and one pair of corresponding sides are equal but the side is not included between the corresponding equal pairs of angles. Are the triangles still congruent? You will observe that they are congruent. Can you reason out why?
You know that the sum of the three angles of a triangle is
So, two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal. We may call it as the AAS Congruence Rule.
Now let us perform the following activity :
Draw triangles with angles
In fact, you can draw as many triangles as you want with different lengths of sides (see Fig. 7.14).
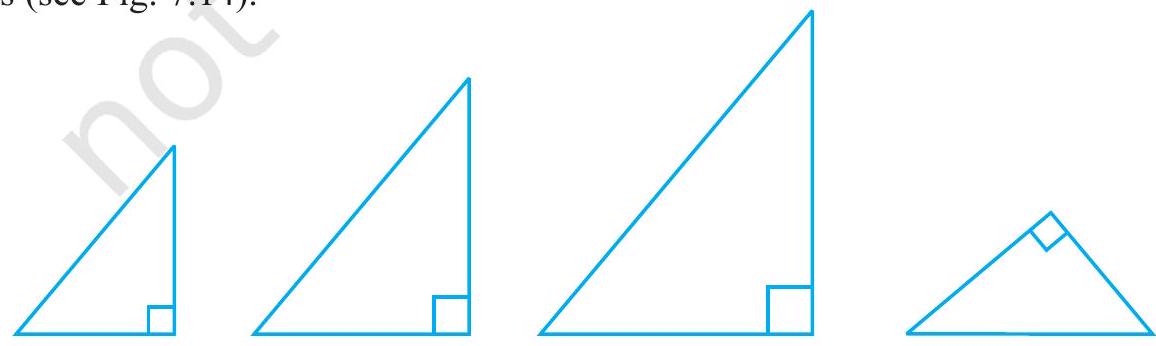
Fig. 7.14
Observe that the triangles may or may not be congruent to each other.
So, equality of three angles is not sufficient for congruence of triangles. Therefore, for congruence of triangles out of three equal parts, one has to be a side.
Let us now take some more examples.
Example 3 : Line-segment
Solution : (i) Consider

Fig. 7.15
Therefore,
(ii)
So,
EXERCISE 7.1
1. In quadrilateral
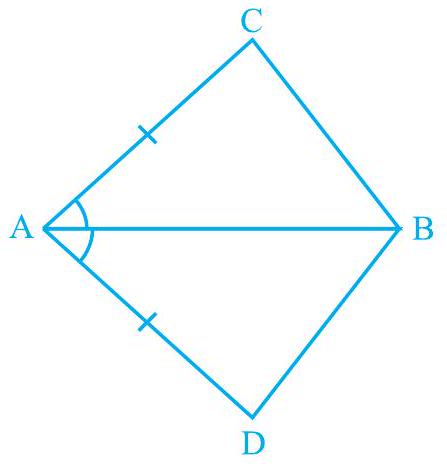
Fig. 7.16
Show Answer
Solution
In
Therefore, BC and BD are of equal lengths.
2.
(i)
(ii)
(iii)
Show Answer
Solution
In
3.
Show Answer
Solution
In
4.

Fig. 7.19
Show Answer
Solution
In
5. Line
(i)
(ii)

Fig. 7.20
Show Answer
Solution
In
BQ (By CPCT)
rms of
6. In Fig. 7.21,

Fig. 7.21
Show Answer
Solution
It is given that
In
(Given)
7.
(i)
(ii)
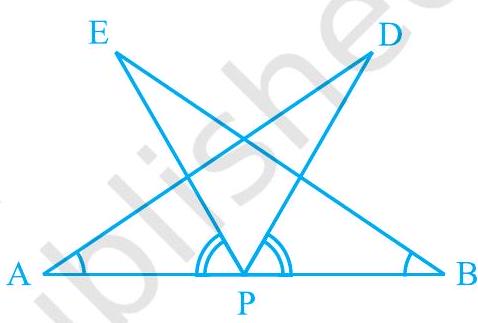
Fig. 7.22
Show Answer
Solution
It is given that EPA
In
8. In right triangle
(i)
(ii)
(iii)
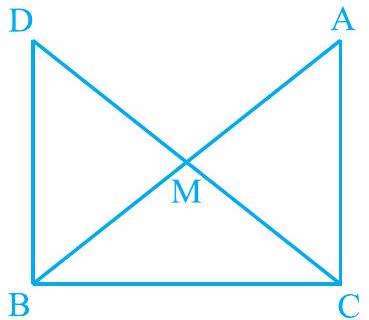
Fig. 7.23
(iv)
Show Answer
Solution
(i) In
However, AेंCM and ¿BDM are alternate interior angles.
Since alternate angles are equal,
It can be said that
(iii) In
7.4 Some Properties of a Triangle
In the above section you have studied two criteria for congruence of triangles. Let us now apply these results to study some properties related to a triangle whose two sides are equal.
Perform the activity given below:
Construct a triangle in which two sides are equal, say each equal to
Do you remember what is such a triangle called?
A triangle in which two sides are equal is called an isosceles triangle. So,

Fig. 7.24
Now, measure
Repeat this activity with other isosceles triangles with different sides.
You may observe that in each such triangle, the angles opposite to the equal sides are equal.
This is a very important result and is indeed true for any isosceles triangle. It can be proved as shown below.
Theorem 7.2 : Angles opposite to equal sides of an isosceles triangle are equal. This result can be proved in many ways. One of the proofs is given here.
Proof : We are given an isosceles triangle
Let us draw the bisector of

Fig. 7.25
In
So,
So,
Is the converse also true? That is:
If two angles of any triangle are equal, can we conclude that the sides opposite to them are also equal?
Perform the following activity.
Construct a triangle

Fig. 7.26
Cut out the triangle from the sheet of paper and fold it along
What can you say about sides
Observe that
So,
Repeat this activity with some more triangles. Each time you will observe that the sides opposite to equal angles are equal. So we have the following:
Theorem 7.3 : The sides opposite to equal angles of a triangle are equal.
This is the converse of Theorem 7.2.
You can prove this theorem by ASA congruence rule.
Let us take some examples to apply these results.
Example 4 : In

Fig. 7.27
Solution : In
So,
So,
or,
Example 5:

Fig. 7.28
Solution : In
So,
Therefore,
Example 6 : In an isosceles triangle

Fig. 7.29
Solution : In
Also,
So,
That is,
So,
This gives
EXERCISE 7.2
1. In an isosceles triangle
(i)
(ii)
Show Answer
Solution

(i) It is given that in triangle
(ii) In
Therefore,
2. In
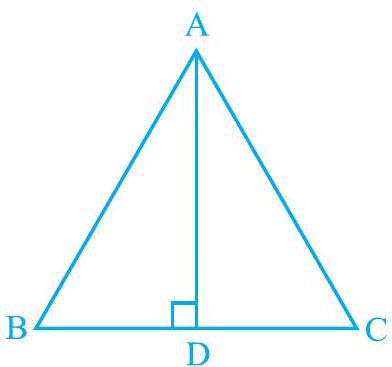
Fig. 7.30
Show Answer
Solution
In
Therefore,
3.
Show Answer
Solution
In
4.
(i)
(ii)
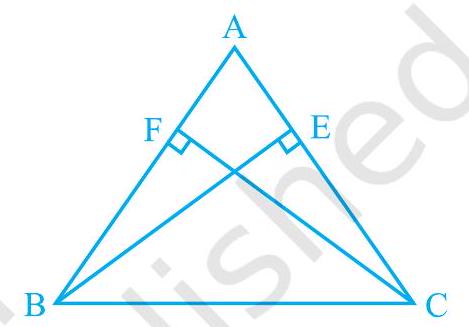
Fig. 7.32
Show Answer
Solution
(i) In
(ii) It has already been proved that
5.
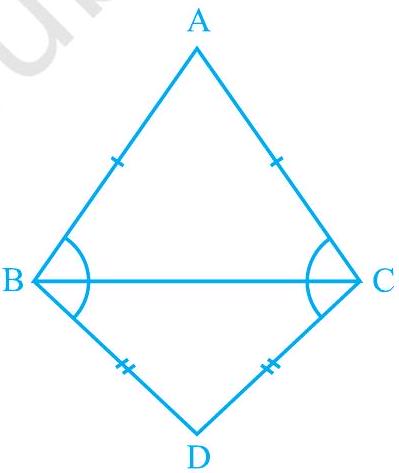
Fig. 7.33
Show Answer
Solution
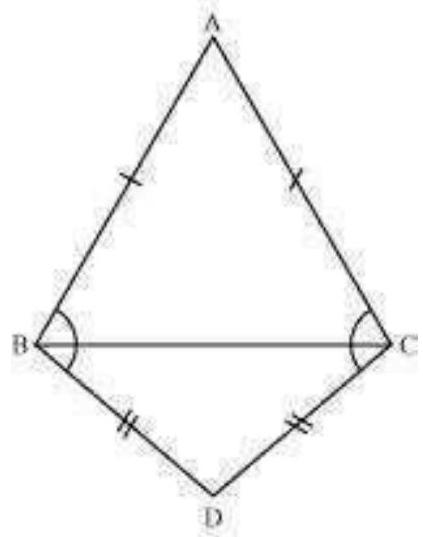
Let us join
In
6.
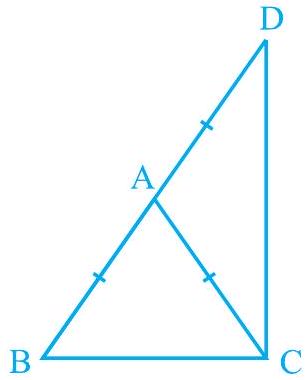
Fig. 7.34
Show Answer
Solution
In
In
In
7.
Show Answer
Solution
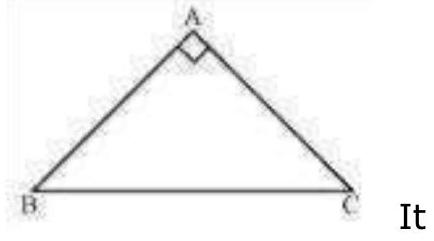
It is given that
In
8. Show that the angles of an equilateral triangle are
Show Answer
Solution
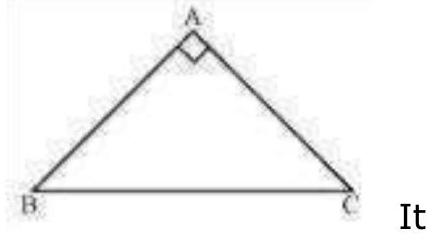
Let us consider that
Therefore,
Also,
Therefore, we obtain
In
7.5 Some More Criteria for Congruence of Triangles
You have seen earlier in this chapter that equality of three angles of one triangle to three angles of the other is not sufficient for the congruence of the two triangles. You may wonder whether equality of three sides of one triangle to three sides of another triangle is enough for congruence of the two triangles. You have already verified in earlier classes that this is indeed true.
To be sure, construct two triangles with sides 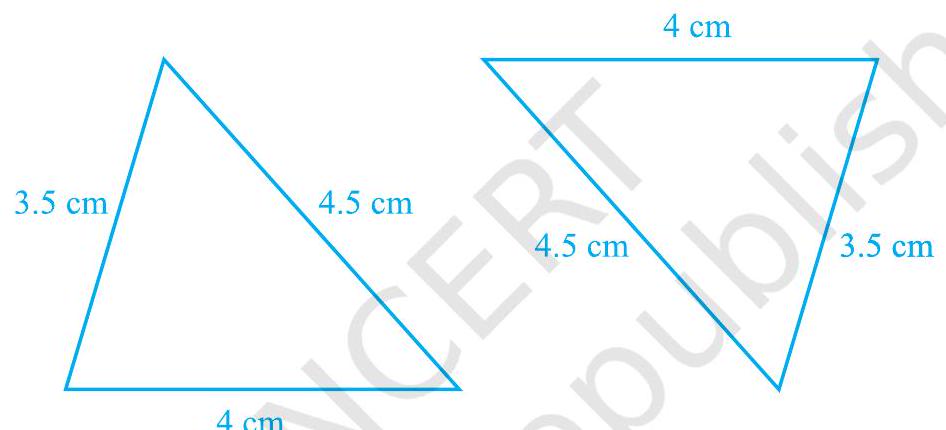
Fig. 7.35
Repeat this activity with some more triangles. We arrive at another rule for congruence.
Theorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
This theorem can be proved using a suitable construction.
You have already seen that in the SAS congruence rule, the pair of equal angles has to be the included angle between the pairs of corresponding pair of equal sides and if this is not so, the two triangles may not be congruent.
Perform this activity:
Construct two right angled triangles with hypotenuse equal to 
Fig. 7.36
Cut them out and place one triangle over the other with equal side placed on each other. Turn the triangles, if necessary. What do you observe?
The two triangles cover each other completely and so they are congruent. Repeat this activity with other pairs of right triangles. What do you observe?
You will find that two right triangles are congruent if one pair of sides and the hypotenuse are equal. You have verified this in earlier classes.
Note that, the right angle is not the included angle in this case.
So, you arrive at the following congruence rule:
Theorem 7.5 (RHS congruence rule) : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Note that RHS stands for Right angle - Hypotenuse - Side.
Let us now take some examples.
Example 7 :
Solution : You are given that
Can you think of two congruent triangles in this figure?
Let us take

Fig. 7.37
In these triangles,
Now let us consider
From (1) and (2), you can easily conclude that PQ is the perpendicular bisector of AB.
[Note that, without showing the congruence of
and
It is because these results give us SSA rule which is not always valid or true for congruence of triangles. Also the angle is not included between the equal pairs of sides.]
Let us take some more examples.
Example 8 :
Solution : You are given that lines
You are to show that
Let us consider

Fig. 7.38
So,
So,
Note that this result is the converse of the result proved in Q. 5 of Exercise 7.1.
EXERCISE 7.3
1.
(i)
(ii)
(iii) AP bisects
(iv)
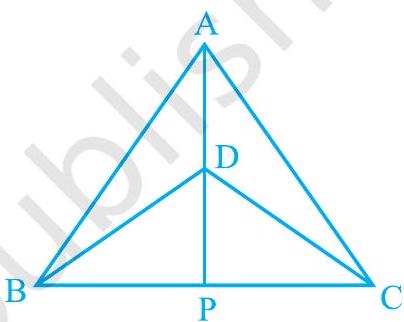
Fig. 7.39
Show Answer
Solution
(i) In
(ii) In
(iii) Since
So,
i.e. AP bisects
In
DP
So, AP bisects
From (iii) and (iv),
AP bisects
(iv) We know that
Also,
Hence,
2.
(i)
(ii)
Show Answer
Solution
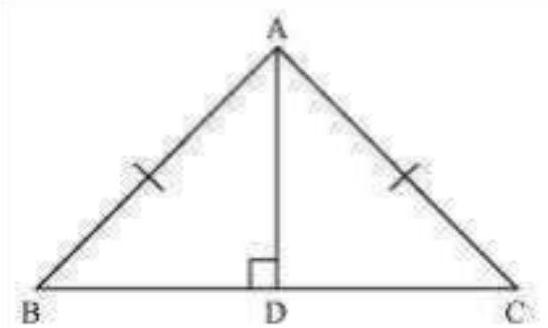
(i) In
Hence,
(ii) Also, by CPCT,
bisects A. :
3. Two sides
(i) 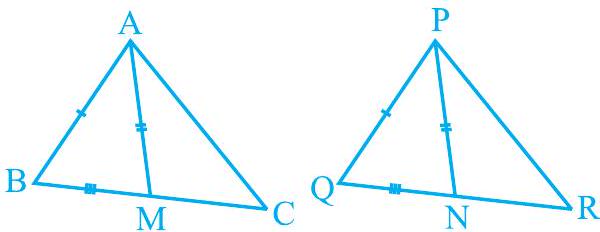
(ii)
Fig. 7.40
Show Answer
Solution
(i) In
However,
In
(ii) In
4.
Show Answer
Solution
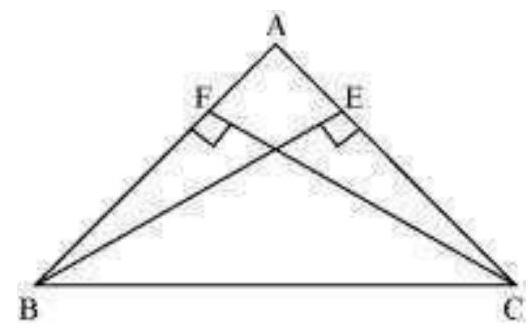
In
Hence,
5.
Show Answer
Solution
In
7.6 Summary
In this chapter, you have studied the following points :
1. Two figures are congruent, if they are of the same shape and of the same size.
2. Two circles of the same radii are congruent.
3. Two squares of the same sides are congruent.
4. If two triangles
5. If two sides and the included angle of one triangle are equal to two sides and the included angle of the other triangle, then the two triangles are congruent (SAS Congruence Rule).
6. If two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, then the two triangles are congruent (ASA Congruence Rule).
7. If two angles and one side of one triangle are equal to two angles and the corresponding side of the other triangle, then the two triangles are congruent (AAS Congruence Rule).
8. Angles opposite to equal sides of a triangle are equal.
9. Sides opposite to equal angles of a triangle are equal.
10. Each angle of an equilateral triangle is of
11. If three sides of one triangle are equal to three sides of the other triangle, then the two triangles are congruent (SSS Congruence Rule).
12. If in two right triangles, hypotenuse and one side of a triangle are equal to the hypotenuse and one side of other triangle, then the two triangles are congruent (RHS Congruence Rule).
7.1 भूमिका
आप पिछली कक्षाओं में, त्रिभुजों और उनके विभिन्न गुणों के बारे में अध्ययन कर चुके हैं। आप जानते हैं कि तीन प्रतिच्छेदी रेखाओं द्वारा बनाई गई एक बंद आकृति (closed figure) एक त्रिभुज (triangle) कहलाती है (‘त्रि’ का अर्थ है ‘तीन’)। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। उदाहरणार्थ, आकृति 7.1 में दिए त्रिभुज
अध्याय 6 में, आप त्रिभुजों के कुछ गुणों का भी अध्ययन कर चुके हैं। इस अध्याय में, आप त्रिभुजों की सर्वांगसमता (congruence), सर्वांगसमता के नियमों, त्रिभुजों के कुछ अन्य गुणों और त्रिभुजों में असमिकाओं (inequalities) के बारे में विस्तृत रूप से अध्ययन करेंगे। आप पिछली कक्षाओं के इन गुणों में से अधिकतर गुणों की सत्यता की जाँच क्रियाकलापों द्वारा कर चुके हैं। यहाँ हम इनमें से कुछ गुणों को सिद्ध भी करेंगे।

आकृति 7.1
7.2 त्रिभुजों की सर्वांगसमता
आपने यह अवश्य ही देखा होगा कि आपकी फोटो की एक ही साइज की दो प्रतियाँ सर्वसम (identical) होती हैं। इसी प्रकार, एक ही माप की दो चूड़ियाँ और एक ही बैंक द्वारा जारी किए गए दो एटीएम (ATM) कार्ड सर्वसम होते हैं। आपने देखा होगा कि यदि एक ही वर्ष
में ढले (बने) दो एक रुपए के सिक्कों में से एक को दूसरे पर रखें, तो वे एक दूसरे को पूर्णतया ढक लेते हैं।
क्या आपको याद है कि ऐसी आकृतियों को कैसी आकृतियाँ कहते हैं? निःसंदेह ये सर्वांगसम आकृतियाँ (congruent figures) कहलाती हैं (‘सर्वांगसम’ का अर्थ है ‘सभी प्रकार से बराबर’, अर्थात् वे आकृतियाँ जिनके समान आकार और समान माप हैं)।
अब एक ही त्रिज्या के दो वृत्त खींचिए और एक को दूसरे पर रखिए। आप क्या देखते हैं? ये एक दूसरे को पूर्णतया ढक लेते हैं और हम इन्हें सर्वांगसम वृत्त कहते हैं।
इसी क्रियाकलाप की एक ही माप की भुजाओं वाले दो वर्गों को खींच कर और फिर एक वर्ग को दूसरे वर्ग पर रखकर (देखिए आकृति 7.2) अथवा बराबर भुजाओं वाले दो समबाहु त्रिभुजों को एक दूसरे पर रखकर, पुनरावृत्ति कीजिए। आप देखेंगे कि वर्ग सर्वांगसम हैं और समबाहु त्रिभुज भी
 आकृति 7.2 सर्वांगसम हैं।
आकृति 7.2 सर्वांगसम हैं।
आप सोच सकते हैं कि हम सर्वांगसमता का अध्ययन क्यों कर रहे हैं। आपने अपने रेफ्रीजरेटर में बर्फ की ट्रे (ice tray) अवश्य ही देखी होगी। ध्यान दीजिए कि बर्फ जमाने के लिए बने सभी खाँचे सर्वांगसम हैं। ट्रे में (खाँचों के लिए प्रयोग किए गए साँचों की गहराइयाँ भी सर्वांगसम होती हैं (ये सभी आयताकार या सभी वृत्ताकार या सभी त्रिभुजाकार हो सकते हैं)। अतः, जब भी सर्वसम (एक जैसी) वस्तुएँ बनानी होती हैं, तो साँचे बनाने के लिए सर्वांगसमता की संकल्पना का प्रयोग किया जाता है।
कभी-कभी आपको अपने पेन के रिफिल (refill) बदलने में भी कठिनाई हो सकती है, यदि नया रिफिल आपके पेन के साइज का न हो। स्पष्टतः रिफिल तभी पेन में लग पाएगा, जबकि पुरानी रिफिल और नया रिफिल सर्वांगसम होंगे। इस प्रकार, आप दैनिक जीवन की स्थितियों में ऐसे अनेक उदाहरण ज्ञात कर सकते हैं, जहाँ वस्तुओं की सर्वांगसमता का उपयोग होता है।
क्या आप सर्वांगसम आकृतियों के कुछ और उदाहरण सोच सकते हैं?
अब, निम्न में से कौन-कौन सी आकृतियाँ आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम नहीं हैं?
आकृति 7.3 (ii) और आकृति 7.3 (iii) में दिए बड़े वर्ग स्पष्टतः आकृति 7.3 (i) के वर्ग के सर्वांगसम नहीं हैं। परन्तु आकृति 7.3 (iv) में दिया हुआ वर्ग आकृति 7.3 (i) में दिए वर्ग के सर्वांगसम है।

(i)

(ii)

(iii)

(iv)
आकृति 7.3
आइए अब दो त्रिभुजों की सर्वांगसमता की चर्चा करें।
आप पहले से यह जानते हैं कि दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की भुजाएँ और कोण दूसरे त्रिभुज की संगत भुजाओं और कोणों के बराबर हों।
अब, निम्न में से कौन-कौन से त्रिभुज आकृति 7.4 (i) में दिए त्रिभुज

(i)

(ii)

R

E
(iii)
(iv)
आकृति 7.4
आकृति 7.4 (ii) से आकृति 7.4 (v) तक के प्रत्येक त्रिभुज को काट कर उसे पलट कर
यदि
ध्यान दीजिए कि जब
अर्थात् भुजा
ध्यान दीजिए कि इस संगतता के अंतर्गत,
इसी प्रकार, आकृति 7.4 (iii) के लिए,
तथा
इसलिए,
आकृति 7.4 (iv) के त्रिभुज और
अतः, त्रिभुजों की सर्वांगसमता को सांकेतिक रूप में लिखने के लिए, उनके शीर्षों की संगतता को सही प्रकार से लिखना आवश्यक है।
ध्यान दीजिए कि सर्वांगसम त्रिभुजों में संगत भाग बराबर होते हैं और ‘सर्वांगसम त्रिभुजों के संगत भागों के लिए’ हम संक्षेप में ’
7.3 त्रिभुजों की सर्वांगसमता के लिए कसौटियाँ
पिछली कक्षाओं में, आप त्रिभुजों की सर्वांगसमता के लिए चार कसौटियाँ (criteria) या नियम (rules) पढ़ चुके हैं। आइए इनका पुनर्विलोकन करें।
एक भुजा

(i)

(ii)
आकृति 7.5
अब दो त्रिभुज खींचिए जिनमें एक भुजा 
आकृति 7.6
देखिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
इस क्रियाकलाप को त्रिभुजों के कुछ और युग्म खींच कर दोहराइए।
अतः, भुजाओं के एक युग्म की समता अथवा भुजाओं के एक युग्म और कोणों के एक युग्म की समता हमें सर्वांगसम त्रिभुज देने के लिए पर्याप्त नहीं है।
उस स्थिति में क्या होगा जब बराबर कोणों की भुजाओं का अन्य युग्म भी बराबर हो जाए?
आकृति 7.7 में
पिछली कक्षाओं से याद कीजिए कि इस स्थिति में, दोनों त्रिभुज सर्वांगसम होते हैं। आप इसका सत्यापन, 
आकृति 7.7
यह त्रिभुजों की सर्वांगसमता की पहली कसौटी (criterion) है।
अभिगृहीत 7.1 (SAS सर्वांगसमता नियम): दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज की दो भुजाएँ और उनका अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और उनके अंतर्गत कोण के बराबर हों।
इस परिणाम को इससे पहले ज्ञात परिणामों की सहायता से सिद्ध नहीं किया जा सकता है और इसीलिए इसे एक अभिगृहीत के रूप में सत्य मान लिया गया है (देखिए परिशिष्ट 1)।
आइए अब कुछ उदाहरण लें।
उदाहरण 1 : आकृति 7.8 में
(i)
(ii)
हल : (i)

आकृति 7.8
साथ ही, क्योंकि
इसलिए,
उदाहरण 2 :
हल :
अतः,
इसलिए,

आकृति 7.9
आइए अब दो त्रिभुजों की रचना करें जिनकी दो भुजाएँ 
आकृति 7.10
ध्यान दीजिए कि ये दोनों त्रिभुज सर्वांगसम नहीं हैं।
त्रिभुजों के कुछ अन्य युग्म लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि दोनों त्रिभुजों की सर्वांगसमता के लिए यह आवश्यक है कि बराबर कोण बराबर भुजाओं के अंतर्गत कोण हो।
अतः, SAS नियम तो सत्य है, परन्तु ASS या SSA नियम सत्य नहीं है।
अब, ऐसे दो त्रिभुजों की रचना करने का प्रयत्न करिए, जिनमें दो कोण


आकृति 7.11
इन दोनों त्रिभुजों को काटिए और एक त्रिभुज को दूसरे के ऊपर रखिए। आप क्या देखते हैं? देखिए कि एक त्रिभुज दूसरे त्रिभुज को पूर्णतया ढक लेता है, अर्थात् दोनों त्रिभुज सर्वांगसम हैं। कुछ और त्रिभुजों को लेकर इस क्रियाकलाप को दोहराइए। आप देखेंगे कि त्रिभुजों की सर्वांगसमता के लिए, दो कोणों और उनकी अंतर्गत भुजा की समता पर्याप्त है।
यह परिणाम कोण-भुजा-कोण (Angle-Side-Angle) कसौटी है और इसे ASA सर्वांगसमता कसौटी लिखा जाता है। आप पिछली कक्षाओं में, इसकी सत्यता की जाँच कर चुके हैं। आइए इस परिणाम को सिद्ध करें।
चूँकि इस परिणाम को सिद्ध किया जा सकता है, इसलिए इसे एक प्रमेय (theorem) कहा जाता है। इसे सिद्ध करने के लिए, हम SAS सर्वांगसमता नियम का प्रयोग करेंगे। प्रमेय 7.1 (ASA सर्वांगसमता नियम) : दो त्रिभुज सर्वांगसम होते हैं, यदि एक त्रिभुज के दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उनकी अंतर्गत भुजा के बराबर हों।
उपपत्ति : हमें दो त्रिभुज
दोनों त्रिभुजों की सर्वांगसमता के लिए देखिए कि यहाँ तीन स्थितियाँ संभव हैं।
स्थिति (i) : मान लीजिए
अब आप क्या देखते हैं? आप देख सकते हैं कि
अतः,

आकृति 7.12
स्थिति (ii) : मान लीजिए, यदि संभव है तो, 
आकृति 7.13
अब
अतः, हम निष्कर्ष निकाल सकते हैं कि
चूँकि दोनों त्रिभुज सर्वांगसम हैं, इसलिए इनके संगत भाग बराबर होने चाहिए।
अतः,
परन्तु हमें दिया है कि
अतः,
परन्तु क्या यह संभव है?
यह तभी संभव है, जब
या
अतः,
(SAS अभिगृहीत द्वारा)
स्थिति (iii) : यदि
अब मान लीजिए कि दो त्रिभुजों में दो कोणों के युग्म और संगत भुजाओं का एक युग्म बराबर हैं, परन्तु ये भुजाएँ बराबर कोणों के युग्मों की अंतर्गत भुजाएँ नहीं हैं। क्या ये त्रिभुज अभी भी सर्वांगसम हैं? आप देखेंगे कि ये त्रिभुज सर्वांगसम हैं। क्या आप इसका कारण बता सकते हैं?
आप जानते हैं कि त्रिभुज के तीनों कोणों का योग
अतः, दो त्रिभुज सर्वांगसम होते हैं, यदि इन त्रिभुजों के दो कोणों के युग्म बराबर हों और संगत भुजाओं का एक युग्म बराबर हो। हम इसे AAS सर्वांगसमता नियम कह सकते हैं।
आइए अब निम्नलिखित क्रियाकलाप करें :
आप ऐसे कितने त्रिभुज खींच सकते हें? वास्तव में, भुजाओं की विभिन्न लंबाइयाँ लेकर हम ऐसे जितने चाहे उतने त्रिभुज खींच सकते हैं (देखिए आकृति 7.14)।

आकृति 7.14
देखिए कि ये त्रिभुज सर्वांगसम हो भी सकते हैं और नहीं भी हो सकते हैं।
अतः, तीन कोणों की समता त्रिभुजों की सर्वांगसमता के लिए पर्याप्त नहीं है। इसलिए, त्रिभुजों की सर्वांगसमता के लिए, तीन बराबर भागों में से एक बराबर भाग भुजा अवश्य होना चाहिए।
आइए अब कुछ और उदाहरण लें।
उदाहरण 3 : रेखाखंड
हल : (i)
अत:,
(ii)
अर्थात्

आकृति 7.15
प्रश्नावली 7.1
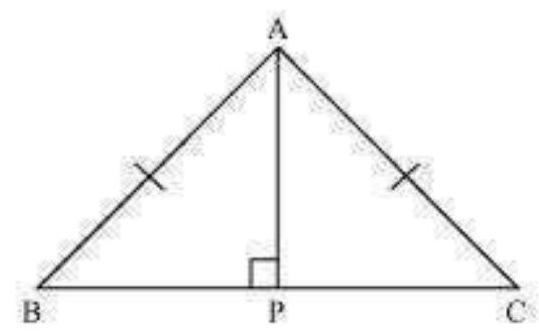
1. चतुर्भुज

आकृति 7.16
2.
(i)
(ii)
(iii)
आकृति 7.17
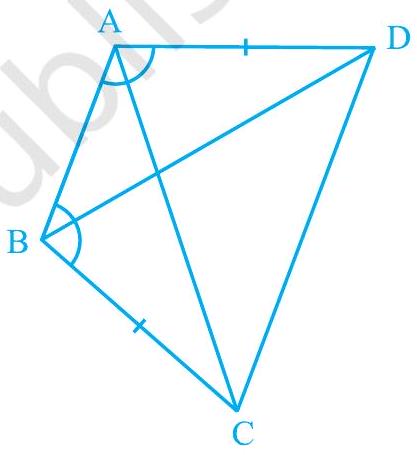
3. एक रेखाखंड
आकृति 7.18
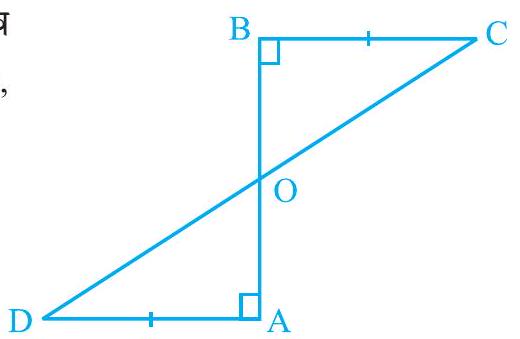
4.
आकृति 7.19
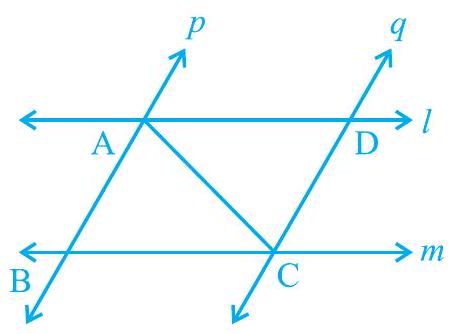
5. रेखा
(i)
(ii)

6. आकृति 7.21 में,

आकृति 7.21
7.
(i)
(ii)

आकृति 7.22
8. एक समकोण त्रिभुज
(i)
(ii)

आकृति 7.23
(iii)
(iv)
7.4 एक त्रिभुज के कुछ गुण
पिछले अनुच्छेद में, आपने त्रिभुजों की सर्वांगसमता की दो कसौटियों का अध्ययन किया है। आइए इन परिणामों का एक ऐसे त्रिभुज के कुछ गुणों का अध्ययन करने में प्रयोग करें जिसकी दो भुजाएँ बराबर होती हैं।
नीचे दिया गया क्रियाकलाप कीजिए:
एक त्रिभुज की रचना कीजिए जिसकी दो भुजाएँ बराबर हों। मान लीजिए दो भुजाएँ

आकृति 7.24
क्या आपको याद है कि इस त्रिभुज को क्या कहते हैं?
एक त्रिभुज जिसकी दो भुजाएँ बराबर हों समद्विबाहु त्रिभुज (isosceles triangle) कहलाता है। अतः, आकृति 7.24 का
अब
विभिन्न भुजाओं वाले अन्य समद्विबाहु त्रिभुज लेकर इस क्रियाकलाप को दोहराइए। आप देख सकते हैं कि ऐसे प्रत्येक त्रिभुज में बराबर भुजाओं के सम्मुख (सामने के) कोण बराबर हैं।
यह एक अति महत्वपूर्ण परिणाम है और प्रत्येक समद्विबाहु त्रिभुज के लिए सत्य है। इसे नीचे दशाई विधि के अनुसार सिद्ध किया जा सकता है:
प्रमेय 7.2 : एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं। इस परिणाम को कई विधियों से सिद्ध किया जा सकता है। इनमें से एक उपपत्ति नीचे दी जा रही है।
उपपत्ति : हमें एक समद्विबाहु

आकृति 7.25
क्या इसका विलोम भी सत्य है? अर्थात्
यदि किसी त्रिभुज के दो कोण बराबर हों, तो क्या हम निष्कर्ष निकाल सकते हैं कि उनकी सम्मुख भुजाएँ भी बराबर होंगी?
नीचे दिया क्रियाकलाप कीजिए :
एक

आकृति 7.26
त्रिभुज
देखिए कि
इसी क्रियाकलाप को ऐसे ही कुछ अन्य त्रिभुज लेकर दोहराइए। प्रत्येक बार आप देखेंगे कि एक त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर हैं। अतः, हम निम्न प्रमेय प्राप्त करते हैं :
प्रमेय 7.3 : किसी त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
यह प्रमेय 7.2 का विलोम है।
आप इस प्रमेय को ASA सर्वांगसमता नियम का प्रयोग करके सिद्ध कर सकते हैं। आइए इन परिणामों को स्पष्ट करने के लिए कुछ उदाहरण लें।
उदाहरण 4 :
हल :

आकृति 7.27
इसी कारण
उदाहरण 5 :
हल :

आकृति 7.28
उदाहरण 6 : एक समद्विबाहु त्रिभुज
साथ ही,
इसलिए,
अर्थात्,

आकृति 7.29
अतः,
इससे प्राप्त होता है:
प्रश्नावली 7.2
1. एक समद्विबाहु त्रिभुज
(i)
(ii)
2.

आकृति 7.30
3.

आकृति 7.31
4.
(i)
(ii)
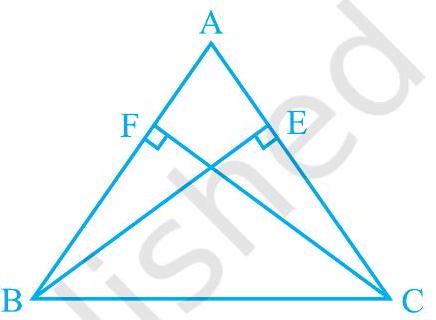
आकृति 7.32
5.
6.

D
आकृति 7.33

आकृति 7.34
7.
8. दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण
7.5 त्रिभुजों की सर्वांगसमता के लिए कुछ और कसौटियाँ
आप इस अध्याय में, पहले यह देख चुके हैं कि एक त्रिभुज के तीनों कोणों के दूसरे त्रिभुज के तीनों कोणों के बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है। आप सोच सकते हैं कि संभवतः एक त्रिभुज की तीनों भुजाओं के दूसरे त्रिभुज की तीनों भुजाओं के बराबर होने पर त्रिभुज सर्वांगसम हो जाएँ। आप यह पिछली कक्षाओं में पढ़ चुके हैं कि ऐसी स्थिति में त्रिभुज नि:संदेह सर्वांगसम होते हैं।
इस धारणा को निश्चित करने के लिए, 
आकृति 7.35
इस क्रियाकलाप को कुछ अन्य त्रिभुज खींचकर दोहराइए। इस प्रकार, हम सर्वांगसमता के एक और नियम पर पहुँच जाते हैं:
प्रमेय 7.4 (SSS सर्वांगसमता नियम) : यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
एक उपयुक्त रचना करके, इस प्रमेय को सिद्ध किया जा सकता है।
आप SAS सर्वांगसमता नियम में पहले ही देख चुके हैं कि बराबर कोणों के युग्म संगत बराबर भुजाओं के युग्मों के बीच में (अंतर्गत) होने चाहिए और यदि ऐसा नहीं हो, तो दोनों त्रिभुज सर्वांगसम नहीं भी हो सकते हैं।
इस क्रियाकलाप को कीजिए :
दो समकोण त्रिभुज ऐसे खींचिए जिनमें प्रत्येक का कर्ण 5 सेमी और एक भुजा


आकृति 7.36
इन्हें काटिए और एक दूसरे पर इस प्रकार रखिए कि इनकी बराबर भुजाएँ एक दूसरे पर आएँ। यदि आवश्यक हो, तो त्रिभुजों को घुमाइए। आप क्या देखते हैं?
आप देखते हैं कि दोनों त्रिभुज एक दूसरे को पूर्णतया ढक लेते हैं और इसीलिए ये सर्वांगसम हैं। यही क्रियाकलाप समकोण त्रिभुजों के अन्य युग्म लेकर दोहराइए। आप क्या देखते हैं?
आप पाएँगे कि दोनों समकोण त्रिभुज सर्वांगसम होंगे, यदि उनके कर्ण बराबर हों और भुजाओं का एक युग्म बराबर हो। आप इस तथ्य की जाँच पिछली कक्षाओं में कर चुके हैं। ध्यान दीजिए कि इस स्थिति में समकोण अंतर्गत कोण नहीं है।
इस प्रकार, आप निम्नलिखित सर्वांगसमता नियम पर पहुँच गए हैं:
प्रमेय 7.5 (RHS सर्वांगसमता नियम ) : यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
ध्यान दीजिए कि यहाँ RHS समकोण (Right angle) - कर्ण (Hypotenuse) - भुजा (Side) को दर्शाता है।
आइए अब कुछ उदाहरण लें।
उदाहरण 7 :

आकृति 7.37 आइए
इन त्रिभुजों में,
अत:,
अब
अतः,
(SAS नियम)
इसलिए,
और
साथ ही,
इसलिए,
या,
(1) और (2) से, आप निष्कर्ष निकाल सकते हैं कि रेखा
[ध्यान दीजिए कि
आइए कुछ और उदाहरण लें।
उदाहरण 8 : बिंदु
हल : आपको दिया है कि रेखाएँ
आपको दर्शाना है कि
अब,

आकृति 7.38
अत:
इसलिए,
ध्यान दीजिए कि यह परिणाम प्रश्नावली 7.1 के प्रश्न 5 में सिद्ध किए गए परिणाम का विलोम है।
प्रश्नावली 7.3
1.
(i)
(ii)

आकृति 7.39
(iii)
(iv)
2.
(i)
3. एक त्रिभुज
(i)

आकृति 7.40
(ii)
4.
5.
7.6 सारांश
इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:
1. दो आकृतियाँ सर्वांगसम होती हैं, यदि उनका एक ही आकार हो और एक ही माप हो।
2. समान त्रिज्याओं वाले दो वृत्त सर्वांगसम होते हैं।
3. समान भुजाओं वाले दो वर्ग सर्वांगसम होते हैं।
4. यदि त्रिभुज
5. यदि एक त्रिभुज की दो भुजाएँ और अंतर्गत कोण दूसरे त्रिभुज की दो भुजाओं और अंतर्गत कोण के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SAS सर्वांगसमता नियम)।
6. यदि एक त्रिभुज के दो कोण और अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और अंतर्गत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (ASA सर्वांगसमता नियम)।
7. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।
8. त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
9. त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
10. किसी समबाहु त्रिभुज का प्रत्येक कोण
11. यदि एक त्रिभुज की तीनों भुजाएँ दूसरे त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (SSS सर्वांगसमता नियम)।
12. यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (RHS सर्वांगसमता नियम)।






