Chapter-07 Alternating Current
7.1 INTRODUCTION
We have so far considered direct current (dc) sources and circuits with dc sources. These currents do not change direction with time. But voltages and currents that vary with time are very common. The electric mains supply in our homes and offices is a voltage that varies like a sine function with time. Such a voltage is called alternating voltage (ac voltage) and the current driven by it in a circuit is called the alternating current (ac current)*. Today, most of the electrical devices we use require ac voltage. This is mainly because most of the electrical energy sold by power companies is transmitted and distributed as alternating current. The main reason for preferring use of ac voltage over dc voltage is that ac voltages can be easily and efficiently converted from one voltage to the other by means of transformers. Further, electrical energy can also be transmitted economically over long distances. AC circuits exhibit characteristics which are exploited in many devices of daily use. For example, whenever we tune our radio to a favourite station, we are taking advantage of a special property of ac circuits - one of many that you will study in this chapter.
- The phrases ac voltage and ac current are contradictory and redundant, respectively, since they mean, literally, alternating current voltage and alternating current current. Still, the abbreviation ac to designate an electrical quantity displaying simple harmonic time dependance has become so universally accepted that we follow others in its use. Further, voltage – another phrase commonly used means potential difference between two points
7.2 AC Voltage Applied to a Resistor
>
Nicola Tesla (1856 –1943) Serbian-Americanscientist, inventor andgenius. He conceived theidea of the rotatingmagnetic field, which is thebasis of practically allalternating currentmachinery, and whichhelped usher in the age ofelectric power. He alsoinvented among otherthings the induction motor,the polyphase system of acpower, and the highfrequency induction coil(the Tesla coil) used in radioand television sets andother electronic equipment.The SI unit of magnetic fieldis named in his honour.
Figure 7.1 shows a resistor connected to a source $\varepsilon$ of ac voltage. The symbol for an ac source in a circuit diagram is $\Theta$. We consider a source which produces sinusoidally varying potential difference across its terminals. Let this potential difference, also called ac voltage, be given by
$$ \begin{equation*} v=v_{m} \sin \omega t \tag{7.1} \end{equation*} $$
where $v_{m}$ is the amplitude of the oscillating potential difference and $\omega$ is its angular frequency.

FIGURE 7.1 AC voltage applied to a resistor.
To find the value of current through the resistor, we apply Kirchhoffs loop rule $\sum \varepsilon(t)=0$ (refer to Section 3.13), to the circuit shown in Fig. 7.1 to get
$ v_{m} \sin \omega t=i R $
or $i=\frac{v_{m}}{R} \sin \omega t$
Since $R$ is a constant, we can write this equation as
$$ \begin{equation*} i=i_{m} \sin \omega t \tag{7.2} \end{equation*} $$
where the current amplitude $i_{m}$ is given by
$$ \begin{equation*} i_{m}=\frac{v_{m}}{R} \tag{7.3} \end{equation*} $$

FIGURE 7.2 In a pure resistor, the voltage and current are in phase. The minima, zero and maxima occur at the same respective times.
Equation (7.3) is Ohm’s law, which for resistors, works equally well for both ac and dc voltages. The voltage across a pure resistor and the current through it, given by Eqs. (7.1) and (7.2) are plotted as a function of time in Fig. 7.2. Note, in particular that both $v$ and $i$ reach zero, minimum and maximum values at the same time. Clearly, the voltage and current are in phase with each other.
We see that, like the applied voltage, the current varies sinusoidally and has corresponding positive and negative values during each cycle. Thus, the sum of the instantaneous current values over one complete cycle is zero, and the average current is zero. The fact that the average current is zero, however, does not mean that the average power consumed is zero and that there is no dissipation of electrical energy. As you know, Joule heating is given by $i^{2} R$ and depends on $i^{2}$ (which is always positive whether $i$ is positive or negative) and not on $i$. Thus, there is Joule heating and dissipation of electrical energy when an ac current passes through a resistor.

George Westinghouse(1846 – 1914) A leadingproponent of the use ofalternating current overdirect current. Thus,he came into conflictwith Thomas Alva Edison,an advocate of directcurrent. Westinghousewas convinced that thetechnology of alternatingcurrent was the key tothe electrical future.He founded the famousCompany named after himand enlisted the servicesof Nicola Tesla andother inventors in thedevelopment of alternatingcurrent motors andapparatus for thetransmission of hightension current, pioneeringin large scale lighting.
The instantaneous power dissipated in the resistor is
$$ \begin{equation*} p=i^{2} R=i_{m}^{2} R \sin ^{2} \omega t \tag{7.4} \end{equation*} $$
The average value of $p$ over a cycle is*
$$ \begin{equation*} \bar{p}=<i^{2} R>=<i_{m}^{2} R \sin ^{2} \omega t> \tag{7.5 a} \end{equation*} $$
where the bar over a letter (here, $p$ ) denotes its average value and $<\ldots . .>$ denotes taking average of the quantity inside the bracket. Since, $i_{m}^{2}$ and $R$ are constants,
$$ \begin{equation*} \bar{p}=i_{m}^{2} R<\sin ^{2} \omega t> \tag{7.5 b} \end{equation*} $$
Using the trigonometric identity, $\sin ^{2} \omega t=$ $1 / 2(1-\cos 2 \omega t)$, we have $\left.<\sin ^{2} \omega t>=(1 / 2)(1-<\cos 2 \omega t \right)$ and since $<\cos 2 \omega t>=0^{*}$, we have,
$$ <\sin ^{2} \omega t>=\frac{1}{2} $$
Thus,
$$ \begin{equation*} \bar{p}=\frac{1}{2} i_{m}^{2} R \tag{7.5 c} \end{equation*} $$
To express ac power in the same form as dc power $\left(P=I^{2} R\right)$, a special value of current is defined and used. It is called, root mean square (rms) or effective current (Fig. 7.3) and is denoted by $I_{r m s}$ or $I$.

FIGURE 7.3 The rms current $I$ is related to the peak current $i_{m}$ by $I=i_{m} / \sqrt{2}=0.707 i_{m}$.
- The average value of a function $F(t)$ over a period $T$ is given by $\langle F(t)\rangle=\frac{1}{T} \int_{0}^{T} F(t) \mathrm{d} t$
$<\cos 2 \omega t> \text{=} \frac{1}{T} \int_{0}^{T}\cos 2 \omega tdt \text{=} \frac{1}{T}[\large\frac{\sin 2 \omega t}{2 \omega}]_{0}^{T} \text{=}\frac{1}{2 \omega T}[\sin 2 \omega \text{-}0]=0$
It is defined by
$$ \begin{align*} I=\sqrt{\overline{i^{2}}} & =\sqrt{\frac{1}{2} i_{m}^{2}}=\frac{i_{m}}{\sqrt{2}} \\ & =0.707 i_{m} \tag{7.6} \end{align*} $$
In terms of $I$, the average power, denoted by $P$ is
$$ \begin{equation*} P=\bar{p}=\frac{1}{2} i_{m}^{2} R=I^{2} R \tag{7.7} \end{equation*} $$
Similarly, we define the rms voltage or effective voltage by
$$ \begin{equation*} V=\frac{v_{m}}{\sqrt{2}}=0.707 v_{m} \tag{7.8} \end{equation*} $$
From Eq. (7.3), we have
$$ v_{m}=i_{m} R $$
or, $\frac{v_{m}}{\sqrt{2}}=\frac{i_{m}}{\sqrt{2}} R$
or, $V=I R$
Equation (7.9) gives the relation between ac current and ac voltage and is similar to that in the dc case. This shows the advantage of introducing the concept of rms values. In terms of rms values, the equation for power [Eq. (7.7)] and relation between current and voltage in ac circuits are essentially the same as those for the dc case.
It is customary to measure and specify rms values for ac quantities. For example, the household line voltage of $220 \mathrm{~V}$ is an $\mathrm{rms}$ value with a peak voltage of
$$ v_{m}=\sqrt{2} \quad V=(1.414)(220 \mathrm{~V})=311 \mathrm{~V} $$
In fact, the $I$ or rms current is the equivalent dc current that would produce the same average power loss as the alternating current. Equation (7.7) can also be written as
$$ P=V^{2} / R=I V \quad(\text { since } V=I R) $$
Example 7.1 A light bulb is rated at $100 \mathrm{~W}$ for a $220 \mathrm{~V}$ supply. Find (a) the resistance of the bulb; (b) the peak voltage of the source; and (c) the rms current through the bulb.
Solution
(a) We are given $P=100 \mathrm{~W}$ and $V=220 \mathrm{~V}$. The resistance of the bulb is
$$ R=\frac{V^{2}}{P}=\frac{(220 \mathrm{~V})^{2}}{100 \mathrm{~W}}=484 \Omega $$
(b) The peak voltage of the source is
$$ v_{m}=\sqrt{2} \mathrm{~V}=311 \mathrm{~V} $$
(c) Since, $P=I V$
$$ I=\frac{P}{V}=\frac{100 \mathrm{~W}}{220 \mathrm{~V}}=0.454 \mathrm{~A} $$
7.3 Representation of AC Current and Voltage by Rotating Vectors - Phasors
In the previous section, we learnt that the current through a resistor is in phase with the ac voltage. But this is not so in the case of an inductor, a capacitor or a combination of these circuit elements. In order to show phase relationship between voltage and current in an ac circuit, we use the notion of phasors. The analysis of an ac circuit is facilitated by the use of a phasor diagram. A phasor* is a vector which rotates about the origin with angular speed $\omega$, as shown in Fig. 7.4. The vertical components of phasors $\mathbf{V}$ and $\mathbf{I}$ represent the sinusoidally varying quantities $v$ and $i$. The magnitudes of phasors $\mathbf{V}$ and $\mathbf{I}$ represent the amplitudes or the peak values $v_{m}$ and $i_{m}$ of these oscillating quantities. Figure 7.4(a) shows the voltage and current phasors and their relationship at time $t_{1}$ for the case of an ac sourceconnected to a resistor i.e., corresponding to the circuit shown in Fig. 7.1. The projection of voltage and current phasors on vertical axis, i.e., $v_{m} \sin \omega t$ and $i_{m} \sin \omega t$, respectively represent the value of voltage and current at that instant. As they rotate with frequency $\omega$, curves in Fig. 7.4(b) are generated.

FIGURE 7.4 (a) A phasor diagram for the circuit in Fig 7.1. (b) Graph of $v$ and $i$ versus $\omega t$.
From Fig. 7.4(a) we see that phasors $\mathbf{V}$ and $\mathbf{I}$ for the case of a resistor are in the same direction. This is so for all times. This means that the phase angle between the voltage and the current is zero.
7.4 AC Voltage Applied to an Inductor
Figure 7.5 shows an ac source connected to an inductor. Usually, inductors have appreciable resistance in their windings, but we shall assume that this inductor has negligible resistance. Thus, the circuit is a purely inductive ac circuit. Let the voltage across the source be $v=v_{m} \sin \omega t$. Using the Kirchhoff’s loop rule, $\sum \varepsilon(t)=0$, and since there is no resistor in the circuit,
$$ \begin{equation*} v-L \frac{\mathrm{d} i}{\mathrm{~d} t}=0 \tag{7.10} \end{equation*} $$
where the second term is the self-induced Faraday emf in the inductor; and $L$ is the self-inductance of

FIGURE 7.5 An ac source connected to an inductor.
- Though voltage and current in ac circuit are represented by phasors – rotating vectors, they are not vectors themselves. They are scalar quantities. It so happens that the amplitudes and phases of harmonically varying scalars combine mathematically in the same way as do the projections of rotating vectors of corresponding magnitudes and directions. The rotating vectors that represent harmonically varying scalar quantities are introduced only to provide us with a simple way of adding these quantities using a rule that we already know
the inductor. The negative sign follows from Lenz’s law (Chapter 6). Combining Eqs. (7.1) and (7.10), we have
$$ \begin{equation*} \frac{\mathrm{d} i}{\mathrm{~d} t}=\frac{v}{L}=\frac{v_{m}}{L} \sin \omega t \tag{7.11} \end{equation*} $$
Equation (7.11) implies that the equation for $i(t)$, the current as a function of time, must be such that its slope $\mathrm{d} i / \mathrm{d} t$ is a sinusoidally varying quantity, with the same phase as the source voltage and an amplitude given by $v_{m} / L$. To obtain the current, we integrate $\mathrm{d} i / \mathrm{d} t$ with respect to time:
$$ \int \frac{\mathrm{d} i}{\mathrm{~d} t} \mathrm{~d} t=\frac{v_{m}}{L} \int \sin (\omega t) \mathrm{d} t $$
and get,
$$ i=-\frac{v_{m}}{\omega L} \cos (\omega t)+\text { constant } $$
The integration constant has the dimension of current and is timeindependent. Since the source has an emf which oscillates symmetrically about zero, the current it sustains also oscillates symmetrically about zero, so that no constant or time-independent component of the current exists. Therefore, the integration constant is zero. Using
$$ -\cos (\omega t)=\sin \omega t-\frac{\pi}{2} \text {, we have } $$
$$ \begin{equation*} i=i_{m} \sin \omega t-\frac{\pi}{2} \tag{7.12} \end{equation*} $$
where $i_{m}=\frac{v_{m}}{\omega L}$ is the amplitude of the current. The quantity $\omega L$ is analogous to the resistance and is called inductive reactance, denoted by $X_{L}$ :
$$ \begin{equation*} X_{L}=\omega L \tag{7.13} \end{equation*} $$
The amplitude of the current is, then
$$ \begin{equation*} i_{m}=\frac{v_{m}}{X_{L}} \tag{7.14} \end{equation*} $$
The dimension of inductive reactance is the same as that of resistance and its SI unit is ohm $(\Omega)$. The inductive reactance limits the current in a purely inductive circuit in the same way as the resistance limits the current in a purely resistive circuit. The inductive reactance is directly proportional to the inductance and to the frequency of the current.
A comparison of Eqs. (7.1) and (7.12) for the source voltage and the current in an inductor shows that the current lags the voltage by $\pi / 2$ or one-quarter (1/4) cycle. Figure 7.6 (a) shows the voltage and the current phasors in the present case at instant $t_{1}$. The current phasor $\mathbf{I}$ is $\pi / 2$ behind the voltage phasor $\mathbf{V}$. When rotated with frequency $\omega$ counterclockwise, they generate the voltage and current given by Eqs. (7.1) and (7.12), respectively and as shown in Fig. 7.6(b).

FIGURE 7.6 (a) A Phasor diagram for the circuit in Fig. 7.5. (b) Graph of $v$ and $i$ versus $\omega t$.
We see that the current reaches its maximum value later than the voltage by one-fourth of a period $\left[\frac{T}{4}=\frac{\pi / 2}{\omega}\right]$. You have seen that an inductor has reactance that limits current similar to resistance in a dc circuit. Does it also consume power like a resistance? Let us try to find out.
The instantaneous power supplied to the inductor is
$$ \begin{aligned} p_{L}=i v & =i_{m} \sin \omega t-\frac{\pi}{2} \times v_{m} \sin (\omega t) \end{aligned} $$
$$ \begin{aligned} & =-i_{m} v_{m} \cos (\omega t) \sin (\omega t) \\ & =-\frac{i_{m} v_{m}}{2} \sin (2 \omega t) \end{aligned} $$
So, the average power over a complete cycle is
$$ \begin{aligned} P _{\mathrm{L}} & =\left\langle-\frac{i _{m} v _{m}}{2} \sin (2 \omega t)\right\rangle \end{aligned} $$
$$ \begin{aligned} & =-\frac{i _{m} v _{m}}{2}\langle\sin (2 \omega t)\rangle=0 \end{aligned} $$
since the average of $\sin (2 \omega t)$ over a complete cycle is zero.
Thus, the average power supplied to an inductor over one complete cycle is zero.
Example 7.2 A pure inductor of $25.0 \mathrm{mH}$ is connected to a source of $220 \mathrm{~V}$. Find the inductive reactance and rms current in the circuit if the frequency of the source is $50 \mathrm{~Hz}$.
Solution The inductive reactance,
$$ \begin{aligned} X_{L} & =2 \pi \nu L=2 \times 3.14 \times 50 \times 25 \times 10^{-3} \Omega \\ & =7.85 \Omega \end{aligned} $$
The rms current in the circuit is
$$ I=\frac{V}{X_{L}}=\frac{220 \mathrm{~V}}{7.85 \Omega}=28 \mathrm{~A} $$
7.5 AC Voltage Applied to a Capacitor
Figure 7.7 shows an ac source $\varepsilon$ generating ac voltage $v=v_{m}$ sin $\omega \mathrm{t}$ connected to a capacitor only, a purely capacitive ac circuit.

FIGURE 7.7 An ac source connected to a capacitor. in a dc circuit,
When a capacitor is connected to a voltage source current will flow for the short time required to charge the capacitor. As charge accumulates on the capacitor plates, the voltage across them increases, opposing the current. That is, a capacitor in a dc circuit will limit or oppose the current as it charges. When the capacitor is fully charged, the current in the circuit falls to zero.
When the capacitor is connected to an ac source, as in Fig. 7.7, it limits or regulates the current, but does not completely prevent the flow of charge. The capacitor is alternately charged and discharged as the current reverses each half cycle. Let $q$ be the charge on the capacitor at any time $t$. The instantaneous voltage $v$ across the capacitor is
$$ \begin{equation*} v=\frac{q}{C} \tag{7.15} \end{equation*} $$
From the Kirchhoff’s loop rule, the voltage across the source and the capacitor are equal,
$$ v_{m} \sin \omega t=\frac{q}{C} $$
To find the current, we use the relation $i=\frac{\mathrm{d} q}{\mathrm{~d} t}$
$$ i=\frac{\mathrm{d}}{\mathrm{d} t}\left(v_{m} C \sin \omega t\right)=\omega C v_{m} \cos (\omega t) $$
Using the relation, $\cos (\omega t)=\sin \omega t+\frac{\pi}{2}$, we have
$$ \begin{equation*} i=i_{m} \sin \omega t+\frac{\pi}{2} \tag{7.16} \end{equation*} $$
where the amplitude of the oscillating current is $i_{m}=\omega C v_{m}$. We can rewrite it as
$$ i_{m}=\frac{v_{m}}{(1 / \omega C)} $$
Comparing it to $i_{m}=v_{m} / R$ for a purely resistive circuit, we find that $(1 / \omega C)$ plays the role of resistance. It is called capacitive reactance and is denoted by $X_{c}$,
$$ \begin{equation*} X_{c}=1 / \omega C \tag{7.17} \end{equation*} $$
so that the amplitude of the current is
$$ \begin{equation*} i_{m}=\frac{v_{m}}{X_{C}} \tag{7.18} \end{equation*} $$
The dimension of capacitive reactance is the same as that of resistance and its SI unit is ohm $(\Omega)$. The capacitive reactance limits the amplitude of the current in a purely capacitive circuit in the same way as the resistance limits the current in a purely resistive circuit. But it is inversely proportional to the frequency and the capacitance.

FIGURE 7.8 (a) A Phasor diagram for the circuit in Fig. 7.8. (b) Graph of v and i versus wt.
A comparison of Eq. (7.16) with the equation of source voltage, Eq. (7.1) shows that the current is $\pi / 2$ ahead of voltage. Figure 7.8(a) shows the phasor diagram at an instant $t_{1}$. Here the current phasor $\mathbf{I}$ is $\pi / 2$ ahead of the voltage phasor $\mathbf{V}$ as they rotate counterclockwise. Figure 7.8(b) shows the variation of voltage and current with time. We see that the current reaches its maximum value earlier than the voltage by one-fourth of a period.
The instantaneous power supplied to the capacitor is $$ \begin{align*} p_{c} & =i v=i_{m} \cos (\omega t) v_{m} \sin (\omega t) \\ & =i_{m} v_{m} \cos (\omega t) \sin (\omega t) \\ & =\frac{i_{m} v_{m}}{2} \sin (2 \omega t) \tag{7.19} \end{align*} $$
So, as in the case of an inductor, the average power
$$ \overline{\mathrm{P}} _{C}=\left\langle\frac{i _{m} v _{m}}{2} \sin (2 \omega t)\right\rangle=\frac{i _{m} v _{m}}{2}\langle\sin (2 \omega t)\rangle=0 $$
since $<\sin (2 \omega t)>=0$ over a complete cycle.
Thus, we see that in the case of an inductor, the current lags the voltage by $\pi / 2$ and in the case of a capacitor, the current leads the voltage by $\pi / 2$.
Example 7.3 A lamp is connected in series with a capacitor. Predict your observations for dc and ac connections. What happens in each case if the capacitance of the capacitor is reduced?
Solution When a dc source is connected to a capacitor, the capacitor gets charged and after charging no current flows in the circuit and the lamp will not glow. There will be no change even if $C$ is reduced. With ac source, the capacitor offers capacitative reactance $(1 / \omega C)$ and the current flows in the circuit. Consequently, the lamp will shine. Reducing $C$ will increase reactance and the lamp will shine less brightly than before.
Example 7.4 A $15.0 \mu \mathrm{F}$ capacitor is connected to a $220 \mathrm{~V}$, $50 \mathrm{~Hz}$ source. Find the capacitive reactance and the current (rms and peak) in the circuit. If the frequency is doubled, what happens to the capacitive reactance and the current?
Solution The capacitive reactance is
$$ X_{C}=\frac{1}{2 \pi \nu C}=\frac{1}{2 \pi(50 \mathrm{~Hz})\left(15.0 \times 10^{-6} \mathrm{~F}\right)}=212 \Omega $$
The rms current is
$$ I=\frac{V}{X_{C}}=\frac{220 \mathrm{~V}}{212 \Omega}=1.04 \mathrm{~A} $$
The peak current is
$$ i_{m}=\sqrt{2} I=(1.41)(1.04 A)=1.47 A $$
This current oscillates between $+1.47 \mathrm{~A}$ and $-1.47 \mathrm{~A}$, and is ahead of the voltage by $\pi / 2$.
If the frequency is doubled, the capacitive reactance is halved and consequently, the current is doubled.
Example 7.5 A light bulb and an open coil inductor are connected to an ac source through a key as shown in Fig. 7.9.

FIGURE 7.9
The switch is closed and after sometime, an iron rod is inserted into the interior of the inductor. The glow of the light bulb (a) increases; (b) decreases; (c) is unchanged, as the iron rod is inserted. Give your answer with reasons.
Solution As the iron rod is inserted, the magnetic field inside the coil magnetizes the iron increasing the magnetic field inside it. Hence, the inductance of the coil increases. Consequently, the inductive reactance of the coil increases. As a result, a larger fraction of the applied ac voltage appears across the inductor, leaving less voltage across the bulb. Therefore, the glow of the light bulb decreases.
7.6 AC Voltage Applied to a Series LCR Circuit
Figure 7.10 shows a series LCR circuit connected to an ac source $\varepsilon$. As usual, we take the voltage of the source to be $v=v_{m} \sin \omega t$.

FIGURE 7.10 A series LCR circuit connected to an ac source.
If $q$ is the charge on the capacitor and $i$ the current, at time $t$, we have, from Kirchhoff’s loop rule:
$$ \begin{equation*} L \frac{\mathrm{d} i}{\mathrm{~d} t}+i R+\frac{q}{C}=v \tag{7.20} \end{equation*} $$
We want to determine the instantaneous current $i$ and its phase relationship to the applied alternating voltage $v$. We shall solve this problem by two methods. First, we use the technique of phasors and in the second method, we solve Eq. (7.20) analytically to obtain the timedependence of $i$.
7.6.1 Phasor-diagram solution
From the circuit shown in Fig. 7.10, we see that the resistor, inductor and capacitor are in series. Therefore, the ac current in each element is the same at any time, having the same amplitude and phase. Let it be
$$ \begin{equation*} i=i_{m} \sin (\omega t+\phi) \tag{7.21} \end{equation*} $$
where $\phi$ is the phase difference between the voltage across the source and the current in the circuit. On the basis of what we have learnt in the previous sections, we shall construct a phasor diagram for the present case.
Let $\mathbf{I}$ be the phasor representing the current in the circuit as given by Eq. (7.21). Further, let $\mathbf{V_\mathbf{L}}, \mathbf{V_\mathbf{R}}, \mathbf{V_\mathbf{C}}$, and $\mathbf{V}$ represent the voltage across the inductor, resistor, capacitor and the source, respectively. From previous section, we know that $\mathbf{V_\mathbf{R}}$ is parallel to $\mathbf{I}, \mathbf{V_\mathbf{C}}$ is $\pi / 2$ behind $\mathbf{I}$ and $\mathbf{V_\mathbf{L}}$ is $\pi / 2$ ahead of $\mathbf{I}$. $\mathbf{V_\mathbf{L}}, \mathbf{V_\mathbf{R}}, \mathbf{V_\mathbf{C}}$ and $\mathbf{I}$ are shown in Fig. 7.11(a) with apppropriate phaserelations.
The length of these phasors or the amplitude of $\mathbf{v_\mathbf{R}}, \mathbf{v_\mathbf{C}}$ and $\mathbf{v_\mathbf{L}}$ are:
$$ \begin{equation*} v_{R m}=i_{m} R, v_{C m}=i_{m} X_{C}, v_{L m}=i_{m} X_{L} \tag{7.22} \end{equation*} $$
The voltage Equation (7.20) for the circuit can be written as
$$ \begin{equation*} v_{\mathrm{L}}+v_{\mathrm{R}}+v_{\mathrm{C}}=v \tag{7.23} \end{equation*} $$
The phasor relation whose vertical component gives the above equation is
$$ \begin{equation*} \mathbf{V} _{\mathbf{L}}+\mathbf{V} _{\mathbf{R}}+\mathbf{V} _{\mathbf{C}}=\mathbf{V} \tag{7.24} \end{equation*} $$

FIGURE 7.11 (a) Relation between the phasors $\mathbf{V_\mathrm{L}}, \mathbf{v_\mathrm{R}}, \mathbf{v_\mathrm{C}}$, and $I$, (b) Relation between the phasors $\mathbf{V_\mathrm{L}}, \mathbf{V_\mathrm{R}}$, and $\left(\mathbf{V_\mathrm{L}}+\mathbf{V_\mathrm{C}}\right)$ for the circuit in Fig. 7.10.
This relation is represented in Fig. 7.11(b). Since $\mathbf{V_\mathbf{C}}$ and $\mathbf{V_\mathbf{L}}$ are always along the same line and in opposite directions, they can be combined into a single phasor $\left(\mathbf{V_\mathbf{C}}+\mathbf{V_\mathbf{L}}\right)$ which has a magnitude $\left|v_{C m}-v_{L m}\right|$. Since $\mathbf{V}$ is represented as the hypotenuse of a right-triangle whose sides are $\mathbf{V_\mathbf{R}}$ and $\left(\mathbf{V_\mathbf{C}}+\mathbf{V_\mathbf{L}}\right)$, the pythagorean theorem gives:
$$ v_{m}^{2}=v_{R m}^{2}+\left(v_{C m}-v_{L m}\right)^{2} $$
Substituting the values of $v_{R m}, v_{C m}$, and $v_{L m}$ from Eq. (7.22) into the above equation, we have
$$ \begin{aligned} v_{m}^{2} & =\left(i_{m} R\right)^{2}+\left(i_{m} X_{C}-i_{m} X_{L}\right)^{2} \\ & =i_{m}^{2} \quad R^{2}+\left(X_{C}-X_{L}\right)^{2} \end{aligned} $$
or, $$ \begin{equation*} i_{m}=\frac{v_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}} \tag{7.25a} \end{equation*} $$
By analogy to the resistance in a circuit, we introduce the impedance $Z$ in an ac circuit:
$$ \begin{equation*} i_{m}=\frac{v_{m}}{Z} \tag{7.25b} \end{equation*} $$
where
$$ \begin{equation*} Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}} \tag{7.26} \end{equation*} $$

FIGURE 7.12 Impedance diagram.
Since phasor $\mathbf{I}$ is always parallel to phasor $\mathbf{V_\mathbf{R}}$, the phase angle $\phi$ is the angle between $\mathbf{V_\mathbf{R}}$ and $\mathbf{V}$ and can be determined from Fig. 7.12:
$\tan \varphi=\frac{v_{C m}-v_{L m}}{v_{R m}}$
Using Eq. (7.22), we have
$\tan \varphi=\frac{X_{C}-X_{L}}{R}$ {7.27}
Equations (7.26) and (7.27) are graphically shown in Fig. (7.12). This is called Impedance diagram which is a right-triangle with $Z$ as its hypotenuse.
Equation 7.25(a) gives the amplitude of the current and Eq. (7.27) gives the phase angle. With these, Eq. (7.21) is completely specified. If $X_{C}>X_{L}, \phi$ is positive and the circuit is predominantly capacitive. Consequently, the current in the circuit leads the source voltage. If $X_{C}<X_{L}, \phi$ is negative and the circuit is predominantly inductive. Consequently, the current in the circuit lags the source voltage.
Figure 7.13 shows the phasor diagram and variation of $v$ and $i$ with $\omega t$ for the case $X_{C}>X_{L}$.

FIGURE 7.13 (a) Phasor diagram of $\mathbf{V}$ and $\mathbf{I}$. (b) Graphs of $v$ and $i$ versus $\omega t$ for a series LCR circuit where $X_{C}>X_{L}$.
Thus, we have obtained the amplitude and phase of current for an $L C R$ series circuit using the technique of phasors. But this method of analysing ac circuits suffers from certain disadvantages. First, the phasor diagram say nothing about the initial condition. One can take any arbitrary value of $t$ (say, $t_{1}$, as done throughout this chapter) and draw different phasors which show the relative angle between different phasors. The solution so obtained is called the steady-state solution. This is not a general solution. Additionally, we do have a transient solution which exists even for $v=0$. The general solution is the sum of the transient solution and the steady-state solution. After a sufficiently long time, the effects of the transient solution die out and the behaviour of the circuit is described by the steady-state solution.
7.6.2 Resonance
An interesting characteristic of the series RLC circuit is the phenomenon of resonance. The phenomenon of resonance is common among systems that have a tendency to oscillate at a particular frequency. This frequency is called the system’s natural frequency. If such a system is driven by an energy source at a frequency that is near the natural frequency, the amplitude of oscillation is found to be large. A familiar example of this for swinging back and forth like a pendulum. If the child pulls on the rope at regular intervals and the frequency of the pulls is almost the same as the frequency of swinging, the amplitude of the swinging will be large (Chapter 13, Class XI).
For an $R L C$ circuit driven with voltage of amplitude $v_{m}$ and frequency $\omega$, we found that the current amplitude is given by
$$ i_{m}=\frac{v_{m}}{Z}=\frac{v_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}} $$
with $X_{c}=1 / \omega C$ and $X_{L}=\omega L$. So if $\omega$ is varied, then at a particular frequency $\omega_{0}, X_{c}=X_{L}$, and the impedance is minimum $\left(Z=\sqrt{R^{2}+0^{2}}=R\right)$. This frequency is called the resonant frequency:
$$ X_{c}=X_{L} \text { or } \frac{1}{\omega_{0} C}=\omega_{0} L $$
$$ \begin{equation*} \text { or } \omega _{0}=\frac{1}{\sqrt{L C}} \tag{7.28} \end{equation*} $$
At resonant frequency, the current amplitude is maximum; $i_{m}=v_{m} / R$.
Figure 7.16 shows the variation of $i_{m}$ with $\omega$ in a $R L C$ series circuit with $L=1.00 \mathrm{mH}, C=$ $1.00 \mathrm{nF}$ for two values of $R$ : (i) $R=100 \Omega$ and (ii) $R=200 \Omega$. For the source applied $v_{m}=$ 100 V. $\omega_{0}$ for this case is $\frac{1}{\sqrt{L C}}=1.00 \times 10^{6}$ $\mathrm{rad} / \mathrm{s}$.
We see that the current amplitude is maximum at the resonant frequency. Since $i_{m}=$ $v_{m} / R$ at resonance, the current amplitude for case (i) is twice to that for case (ii).

FIGURE 7.14 Variation of $i_{m}$ with $\omega$ for two cases: (i) $R=100 \Omega$, (ii) $R=200 \Omega$, $L=1.00 \mathrm{mH}$.
Resonant circuits have a variety of applications, for example, in the tuning mechanism of a radio or a TV set. The antenna of a radio accepts signals from many broadcasting stations. The signals picked up in the antenna acts as a source in the tuning circuit of the radio, so the circuit can be driven at many frequencies. But to hear one particular radio station, we tune the radio. In tuning, we vary the capacitance of a capacitor in the tuning circuit such that the resonant frequency of the circuit becomes nearly equal to the frequency of the radio signal received. When this happens, the amplitude of the current with the frequency of the signal of the particular radio station in the circuit is maximum.
It is important to note that resonance phenomenon is exhibited by a circuit only if both $L$ and $C$ are present in the circuit. Only then do the voltages across $L$ and $C$ cancel each other (both being out of phase) and the current amplitude is $v_{m} / R$, the total source voltage appearing across $R$. This means that we cannot have resonance in a RL or $R C$ circuit.
Example 7.6 A resistor of $200 \Omega$ and a capacitor of $15.0 \mu \mathrm{F}$ are connected in series to a $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ac source. (a) Calculate the current in the circuit; (b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox.
Solution
Given
$R=200 \Omega, C=15.0 \mu \mathrm{F}=15.0 \times 10^{-6} \mathrm{~F}$
$V=220 \mathrm{~V}, v=50 \mathrm{~Hz}$
(a) In order to calculate the current, we need the impedance of the circuit. It is
$ \begin{aligned} Z & =\sqrt{R^{2}+X_{C}^{2}}=\sqrt{R^{2}+(2 \pi \nu C)^{-2}} \\ & =\sqrt{(200 \Omega)^{2}+\left(2 \times 3.14 \times 50 \times 15.0 \times 10^{-6} \mathrm{~F}\right)^{-2}} \end{aligned} $
$ \begin{aligned} & =\sqrt{(200 \Omega)^{2}+(212.3 \Omega)^{2}} \\ & =291.67 \Omega \end{aligned} $
Therefore, the current in the circuit is
$$ I=\frac{V}{Z}=\frac{220 \mathrm{~V}}{291.5 \Omega}=0.755 \mathrm{~A} $$
(b) Since the current is the same throughout the circuit, we have
$$ \begin{aligned} & V_{R}=I R=(0.755 \mathrm{~A})(200 \Omega)=151 \mathrm{~V} \\ & V_{C}=I X_{C}=(0.755 \mathrm{~A})(212.3 \Omega)=160.3 \mathrm{~V} \end{aligned} $$
The algebraic sum of the two voltages, $V_{R}$ and $V_{C}$ is $311.3 \mathrm{~V}$ which is more than the source voltage of $220 \mathrm{~V}$. How to resolve this paradox? As you have learnt in the text, the two voltages are not in the same phase. Therefore, they cannot be added like ordinary numbers. The two voltages are out of phase by ninety degrees. Therefore, the total of these voltages must be obtained using the Pythagorean theorem:
$$ \begin{aligned} V_{R+C} & =\sqrt{V_{R}^{2}+V_{C}^{2}} \\ & =220 \mathrm{~V} \end{aligned} $$
Thus, if the phase difference between two voltages is properly taken into account, the total voltage across the resistor and the capacitor is equal to the voltage of the source.
7.7 Power in AC Circuit: The Power Factor
We have seen that a voltage $v=v_{m} \sin \omega t$ applied to a series $R L C$ circuit drives a current in the circuit given by $i=i_{m} \sin (\omega t+\phi)$ where
$$ i_{m}=\frac{v_{m}}{Z} \text { and } \phi=\tan ^{-1}\left(\frac{X _{C}-X _{L}}{R}\right) $$
Therefore, the instantaneous power $p$ supplied by the source is
$$ \begin{align*} & p=v i=\left(v_{m} \sin \omega t\right) \times\left[i_{m} \sin (\omega t+\varphi)\right] \\ & =\frac{v_{m} i_{m}}{2}[\cos \varphi-\cos (2 \omega t+\varphi)] \tag{7.29} \end{align*} $$
The average power over a cycle is given by the average of the two terms in R.H.S. of Eq. (7.37). It is only the second term which is time-dependent. Its average is zero (the positive half of the cosine cancels the negative half). Therefore,
$$ \begin{align*} & P=\frac{v_{m} i_{m}}{2} \cos \varphi=\frac{v_{m}}{\sqrt{2}} \frac{i_{m}}{\sqrt{2}} \cos \varphi \\ & =V I \cos \varphi \tag{30a} \end{align*} $$
This can also be written as,
$$ \begin{equation*} P=I^{2} Z \cos \varphi \tag{30b} \end{equation*} $$
So, the average power dissipated depends not only on the voltage and current but also on the cosine of the phase angle $\phi$ between them. The quantity $\cos \phi$ is called the power factor. Let us discuss the following cases:
Case (i) Resistive circuit: If the circuit contains only pure $R$, it is called resistive. In that case $\phi=0, \cos \phi=1$. There is maximum power dissipation.
Case (ii) Purely inductive or capacitive circuit: If the circuit contains only an inductor or capacitor, we know that the phase difference between voltage and current is $\pi / 2$. Therefore, $\cos \phi=0$, and no power is dissipated even though a current is flowing in the circuit. This current is sometimes referred to as wattless current.
Case (iii) $L C R$ series circuit: In an LCR series circuit, power dissipated is given by Eq. (7.30) where $\phi=\tan ^{-1}\left(X_{c}-X_{L}\right) / R$. So, $\phi$ may be non-zero in a $R L$ or $R C$ or $R C L$ circuit. Even in such cases, power is dissipated only in the resistor.
Case (iv) Power dissipated at resonance in LCR circuit: At resonance $X_{c}-X_{L}=0$, and $\phi=0$. Therefore, $\cos \phi=1$ and $P=I^{2} Z=I^{2} R$. That is, maximum power is dissipated in a circuit (through $R$ ) at resonance.
Example 7.7 (a) For circuits used for transporting electric power, a low power factor implies large power loss in transmission. Explain.
(b) Power factor can often be improved by the use of a capacitor of appropriate capacitance in the circuit. Explain.
Solution (a) We know that $P=I V \cos \phi$ where $\cos \phi$ is the power factor. To supply a given power at a given voltage, if $\cos \phi$ is small, we have to increase current accordingly. But this will lead to large power loss $\left(I^{2} R\right)$ in transmission.
(b)Suppose in a circuit, current $I$ lags the voltage by an angle $\phi$. Then power factor $\cos \phi=R / Z$.
We can improve the power factor (tending to 1 ) by making $Z$ tend to $R$. Let us understand, with the help of a phasor diagram (Fig. 7.15) how this can be achieved. Let us resolve $\mathbf{I}$ into two components. $\mathbf{I_p}$ along the applied voltage $\mathbf{V}$ and $\mathbf{I_q}$ perpendicular to the applied voltage. $\mathbf{I_q}$ as you have learnt in Section 7.7, is called the wattless component since corresponding to this component of current, there is no power loss. $\mathbf{I_\mathrm{P}}$ is known as the power component because it is in phase with the voltage and corresponds to power loss in the circuit. It’s clear from this analysis that if we want to improve power factor, we must completely neutralize the lagging wattless current $\mathbf{I_\mathrm{q}}$ by an equal leading wattless current $\mathbf{I_q}^{\prime}$. This can be done by connecting a capacitor of appropriate value in parallel so that $\mathbf{I_q}$ and $\mathbf{I_q}^{\prime}$ cancel each other and $P$ is effectively $I_{\mathrm{p}} V$.

FIGURE 7.15
Example 7.8 A sinusoidal voltage of peak value $283 \mathrm{~V}$ and frequency $50 \mathrm{~Hz}$ is applied to a series LCR circuit in which $\mathrm{R}=3 \Omega, L=25.48 \mathrm{mH}$, and $\mathrm{C}=796 \mu \mathrm{F}$. Find (a) the impedance of the circuit; (b) the phase difference between the voltage across the source and the current; (c) the power dissipated in the circuit; and (d) the power factor.
Solution (a) To find the impedance of the circuit, we first calculate $X_{\mathrm{L}}$ and $X_{\mathrm{C}}$.
$$ \begin{aligned} X_L & =2 \pi v L \\ & =2 \times 3.14 \times 50 \times 25.48 \times 10^{-3} \Omega=8 \Omega \\ X_C & =\frac{1}{2 \pi v C} \\ = & \frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}=4 \Omega \end{aligned} $$
Therefore,
$$ \begin{aligned} Z & =\sqrt{R^2+\left(X_L-X_C\right)^2}=\sqrt{3^2+(8-4)^2} \\ & =5 \Omega \end{aligned} $$
(b) Phase difference, $\phi=\tan ^{-1} \frac{X_C-X_L}{R}$
$$ =\tan ^{-1}\left(\frac{4-8}{3}\right)=-53.1^{\circ} $$
Since $\phi$ is negative, the current in the circuit lags the voltage across the source.
(c) The power dissipated in the circuit is
$$ P=I^2 R $$
Now, $I=\frac{i_m}{\sqrt{2}}=\frac{1}{\sqrt{2}}\left(\frac{283}{5}\right)=40 \mathrm{~A}$
Therefore, $P=(40 \mathrm{~A})^2 \times 3 \Omega=4800 \mathrm{~W}$
(d) Power factor $=\cos \phi=\cos \left(-53.1^{\circ}\right)=0.6$
Example 7.9 Suppose the frequency of the source in the previous example can be varied. (a) What is the frequency of the source at which resonance occurs? (b) Calculate the impedance, the current, and the power dissipated at the resonant condition.
Solution
(a) The frequency at which the resonance occurs is
$$ \begin{aligned} \omega_{0} & =\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{25.48 \times 10^{-3} \times 796 \times 10^{-6}}} \\ & =222.1 \mathrm{rad} / \mathrm{s} \end{aligned} $$
$$ \begin{aligned} v_{r} & =\frac{\omega_{0}}{2 \pi}=\frac{221.1}{2 \times 3.14} \mathrm{~Hz}=35.4 \mathrm{~Hz} \end{aligned} $$
(b) The impedance $Z$ at resonant condition is equal to the resistance:
$$ Z=R=3 \Omega $$
The rms current at resonance is
$$ =\frac{V}{Z}=\frac{V}{R}=\frac{283}{\sqrt{2}} \quad \frac{1}{3}=66.7 \mathrm{~A} $$
The power dissipated at resonance is
$$ P=I^{2} \times R=(66.7)^{2} \times 3=13.35 \mathrm{~kW} $$
You can see that in the present case, power dissipated at resonance is more than the power dissipated in Example 7.8.
Example 7.10 At an airport, a person is made to walk through the doorway of a metal detector, for security reasons. If she/he is carrying anything made of metal, the metal detector emits a sound. On what principle does this detector work?
Solution The metal detector works on the principle of resonance in ac circuits. When you walk through a metal detector, you are, in fact, walking through a coil of many turns. The coil is connected to a capacitor tuned so that the circuit is in resonance. When you walk through with metal in your pocket, the impedance of the circuit changes - resulting in significant change in current in the circuit. This change in current is detected and the electronic circuitry causes a sound to be emitted as an alarm.
7.8 TRANSFORMERS
For many purposes, it is necessary to change (or transform) an alternating voltage from one to another of greater or smaller value. This is done with a device called transformer using the principle of mutual induction.
A transformer consists of two sets of coils, insulated from each other. They are wound on a soft-iron core, either one on top of the other as in Fig. 7.16(a) or on separate limbs of the core as in Fig. 7.16(b). One of the coils called the primary coil has $N_{p}$ turns. The other coil is called the secondary coil; it has $N_{s}$ turns. Often the primary coil is the input coil and the secondary coil is the output coil of the transformer.

FIGURE 7.16 Two arrangements for winding of primary and secondary coil in a transformer: (a) two coils on top of each other, (b) two coils on separate limbs of the core.
When an alternating voltage is applied to the primary, the resulting current produces an alternating magnetic flux which links the secondary and induces an emf in it. The value of this emf depends on the number of turns in the secondary. We consider an ideal transformer in which the primary has negligible resistance and all the flux in the core links both primary and secondary windings. Let $\phi$ be the flux in each turn in the core at time $t$ due to current in the primary when a voltage $v_{p}$ is applied to it.
Then the induced emf or voltage $\varepsilon_{s}$, in the secondary with $N_{s}$ turns is
$$ \begin{equation*} \varepsilon_{\mathrm{s}}=-N_{\mathrm{s}} \frac{\mathrm{d} \varphi}{\mathrm{d} t} \tag{7.31} \end{equation*} $$
The alternating flux $\phi$ also induces an emf, called back emf in the primary. This is
$$ \begin{equation*} \varepsilon_{p}=-N_{p} \frac{\mathrm{d} \varphi}{\mathrm{d} t} \tag{7.32} \end{equation*} $$
But $\varepsilon_{p}=v_{p}$. If this were not so, the primary current would be infinite since the primary has zero resistance (as assumed). If the secondary is an open circuit or the current taken from it is small, then to a good approximation
$$ \varepsilon_{s}=v_{s} $$
where $v_{s}$ is the voltage across the secondary. Therefore, Eqs. (7.31) and (7.32) can be written as
$$ \begin{align*} & v_{s}=-N_{s} \frac{d \varphi}{d t} \tag{31a} \\ & v_{p}=-N_{p} \frac{d \varphi}{d t} \tag{32a} \end{align*} $$
From Eqs. [7.31 (a)] and [7.32 (a)], we have
$$ \begin{equation*} \frac{v_{s}}{v_{p}}=\frac{N_{s}}{N_{p}} \tag{7.33} \end{equation*} $$
Note that the above relation has been obtained using three assumptions: (i) the primary resistance and current are small; (ii) the same flux links both the primary and the secondary as very little flux escapes from the core, and (iii) the secondary current is small.
If the transformer is assumed to be 100% efficient (no energy losses), the power input is equal to the power output, and since $p=i v$,
$$ \begin{equation*} i_{p} v_{p}=i_{s} v_{s} \tag{7.34} \end{equation*} $$
Although some energy is always lost, this is a good approximation, since a well designed transformer may have an efficiency of more than 95%. Combining Eqs. (7.33) and (7.34), we have
$$ \begin{equation*} \frac{i_{p}}{i_{s}}=\frac{v_{s}}{v_{p}}=\frac{N_{s}}{N_{p}} \tag{7.35} \end{equation*} $$
Since $i$ and $v$ both oscillate with the same frequency as the ac source, Eq. (7.35) also gives the ratio of the amplitudes or rms values of corresponding quantities.
Now, we can see how a transformer affects the voltage and current. We have:
$$ \begin{equation*} V _{s}=\left(\frac{N _{s}}{N _{p}}\right) V _{p} \quad \text { and } I _{s}=\left(\frac{N _{p}}{N _{s}}\right) I _{p} \tag{7.36} \end{equation*} $$
That is, if the secondary coil has a greater number of turns than the primary $\left(N_{s}>N_{p}\right)$, the voltage is stepped up $\left(V_{s}>V_{p}\right)$. This type of arrangement is called a step-up transformer. However, in this arrangement, there is less current in the secondary than in the primary $\left(N_{p} / N_{s}<1\right.$ and $I_{s}$ $<I_{p}$. For example, if the primary coil of a transformer has 100 turns and the secondary has 200 turns, $N_{s} / N_{p}=2$ and $N_{p} / N_{s}=1 / 2$. Thus, a $220 \mathrm{~V}$ input at $10 \mathrm{~A}$ will step-up to $440 \mathrm{~V}$ output at 5.0 A.
If the secondary coil has less turns than the primary $\left(N_{s}<N_{p}\right)$, we have a step-down transformer. In this case, $V_{s}<V_{p}$ and $I_{s}>I_{p}$. That is, the voltage is stepped down, or reduced, and the current is increased.
The equations obtained above apply to ideal transformers (without any energy losses). But in actual transformers, small energy losses do occur due to the following reasons:
(i) Flux Leakage: There is always some flux leakage; that is, not all of the flux due to primary passes through the secondary due to poor design of the core or the air gaps in the core. It can be reduced by winding the primary and secondary coils one over the other.
(ii) Resistance of the windings: The wire used for the windings has some resistance and so, energy is lost due to heat produced in the wire $\left(I^{2} R\right)$. In high current, low voltage windings, these are minimised by using thick wire.
(iii) Eddy currents: The alternating magnetic flux induces eddy currents in the iron core and causes heating. The effect is reduced by using a laminated core.
(iv) Hysteresis: The magnetisation of the core is repeatedly reversed by the alternating magnetic field. The resulting expenditure of energy in the core appears as heat and is kept to a minimum by using a magnetic material which has a low hysteresis loss.
The large scale transmission and distribution of electrical energy over long distances is done with the use of transformers. The voltage output of the generator is stepped-up (so that current is reduced and consequently, the $I^{2} R$ loss is cut down). It is then transmitted over long distances to an area sub-station near the consumers. There the voltage is stepped down. It is further stepped down at distributing sub-stations and utility poles before a power supply of $240 \mathrm{~V}$ reaches our homes.
SUMMARY
1. An alternating voltage $v=v_{m} \sin \omega t$ applied to a resistor $R$ drives a current $i=i_{m} \sin \omega t$ in the resistor, $i_{m}=\frac{v_{m}}{R}$. The current is in phase with the applied voltage.
2. For an alternating current $i=i_{m} \sin \omega t$ passing through a resistor $R$, the average power loss $P$ (averaged over a cycle) due to joule heating is $(1 / 2) i_{m}^{2} R$. To express it in the same form as the dc power $\left(P=I^{2} R\right)$, a special value of current is used. It is called root mean square (rms) current and is donoted by $I$ :
$$ I=\frac{i_{m}}{\sqrt{2}}=0.707 i_{m} $$
Similarly, the rms voltage is defined by
$$ V=\frac{v_{m}}{\sqrt{2}}=0.707 v_{m} $$
We have $P=I V=I^{2} R$
3. An ac voltage $v=v_{m} \sin \omega t$ applied to a pure inductor $L$, drives a current in the inductor $i=i_{m} \sin (\omega t-\pi / 2)$, where $i_{m}=v_{m} / X_{L} . X_{L}=\omega L$ is called inductive reactance. The current in the inductor lags the voltage by $\pi / 2$. The average power supplied to an inductor over one complete cycle is zero.
4. An ac voltage $v=v_{m} \sin \omega t$ applied to a capacitor drives a current in the capacitor: $i=i_{m} \sin (\omega t+\pi / 2)$. Here,
$i_{m}=\frac{v_{m}}{X_{C}}, X_{C}=\frac{1}{\omega C}$ is called capacitive reactance.
The current through the capacitor is $\pi / 2$ ahead of the applied voltage. As in the case of inductor, the average power supplied to a capacitor over one complete cycle is zero.
5. For a series $R L C$ circuit driven by voltage $v=v_{m} \sin \omega t$, the current is given by $i=i_{m} \sin (\omega t+\phi)$
where $\quad i_{m}=\frac{v_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}}$
and $\varphi=\tan ^{-1} \frac{X_{C}-X_{L}}{R}$
$Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}$ is called the impedance of the circuit.
The average power loss over a complete cycle is given by
$$ P=V I \cos \phi $$
The term $\cos \phi$ is called the power factor.
6. In a purely inductive or capacitive circuit, $\cos \phi=0$ and no power is dissipated even though a current is flowing in the circuit. In such cases, current is referred to as a wattless current.
7. The phase relationship between current and voltage in an ac circuit can be shown conveniently by representing voltage and current by rotating vectors called phasors. A phasor is a vector which rotates about the origin with angular speed $\omega$. The magnitude of a phasor represents the amplitude or peak value of the quantity (voltage or current) represented by the phasor.
The analysis of an ac circuit is facilitated by the use of a phasor diagram.
8. A transformer consists of an iron core on which are bound a primary coil of $N_{p}$ turns and a secondary coil of $N_{s}$ turns. If the primary coil is connected to an ac source, the primary and secondary voltages are related by
$$ V _{s}=\left(\frac{N _{s}}{N _{p}}\right) V _{p} $$
and the currents are related by
$$ I _{s}=\left(\frac{N _{p}}{N _{s}}\right) I _{p} $$
If the secondary coil has a greater number of turns than the primary, the voltage is stepped-up $\left(V_{s}>V_{p}\right)$. This type of arrangement is called a stepup transformer. If the secondary coil has turns less than the primary, we have a step-down transformer.
| Physical quantity | Symbo1 | Dimensions | Unit | Remarks |
|---|---|---|---|---|
| rms voltage | $V$ | $\left[\mathrm{M} \mathrm{L}^2 \mathbf{T}^{-3} \mathrm{~A}^{-1}\right]$ | V | $V=\frac{v_m}{\sqrt{2}}, \quad v_m \quad$ is the amplitude of the ac voltage. |
| rms current | I | $[A]$ | A | $I=\frac{i_m}{\sqrt{2}}, i_{\mathrm{m}}$ is the amplitude of the ac current. |
| Reactance: Inductive Capacttive | $X_L$ $X_c$ |
$\left[\mathrm{M} \mathrm{L}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-2}\right]$ $\left[\mathrm{M} \mathrm{L}^2 \mathbf{T}^{-3} \mathrm{~A}^{-2}\right]$ |
$\Omega$ | $X_{\mathrm{L}}=\omega L$ $X_c=1 / \omega C$ |
| Impedance | $Z$ | $\left[\mathrm{M} \mathrm{L}^2 \mathbf{T}^{-3} \mathrm{~A}^{-2}\right]$ | $\Omega$ | Depends on elements present in the circuit. |
| Resonant frequency |
$\omega_{\mathrm{r}}$ or $\omega_{\mathrm{o}}$ | $\left[\mathrm{~T}^{-1}\right]$ | $\omega_0=\frac{1}{\sqrt{L C}}$ for a | |
| Quality factor | $Q$ | Dimensionles | $Q=\frac{\omega_0 L}{R}=\frac{1}{\omega_0 C R}$ for a series $R L C$ circuit. |
|
| Power factor | Dimensionles | $=\cos \phi, \phi$ is the phase difference between voltage applied and current in the circuit. |
POINTS TO PONDER
1. When a value is given for ac voltage or current, it is ordinarily the rms value. The voltage across the terminals of an outlet in your room is normally $240 \mathrm{~V}$. This refers to the $r m s$ value of the voltage. The amplitude of this voltage is
$$ v_{m}=\sqrt{2} \mathrm{~V}=\sqrt{2}(240)=340 \mathrm{~V} $$
2. The power rating of an element used in ac circuits refers to its average power rating.
3. The power consumed in an ac circuit is never negative.
4. Both alternating current and direct current are measured in amperes. But how is the ampere defined for an alternating current? It cannot be derived from the mutual attraction of two parallel wires carrying ac currents, as the dc ampere is derived. An ac current changes direction with the source frequency and the attractive force would average to zero. Thus, the ac ampere must be defined in terms of some property that is independent of the direction of the current. Joule heating is such a property, and there is one ampere of rms value of alternating current in a circuit if the current produces the same average heating effect as one ampere of dc current would produce under the same conditions.
5. In an ac circuit, while adding voltages across different elements, one should take care of their phases properly. For example, if $V_{R}$ and $V_{C}$ are voltages across $R$ and $C$, respectively in an $R C$ circuit, then the total voltage across $R C$ combination is $V_{R C}=\sqrt{V_{R}^{2}+V_{C}^{2}}$ and not $V_{R}+V_{C}$ since $V_{C}$ is $\pi / 2$ out of phase of $V_{R}$.
6. Though in a phasor diagram, voltage and current are represented by vectors, these quantities are not really vectors themselves. They are scalar quantities. It so happens that the amplitudes and phases of harmonically varying scalars combine mathematically in the same way as do the projections of rotating vectors of corresponding magnitudes and directions. The ‘rotating vectors’ that represent harmonically varying scalar quantities are introduced only to provide us with a simple way of adding these quantities using a rule that we already know as the law of vector addition.
7. There are no power losses associated with pure capacitances and pure inductances in an ac circuit. The only element that dissipates energy in an ac circuit is the resistive element.
8. In a RLC circuit, resonance phenomenon occur when $X_{L}=X_{C}$ or $\omega_{0}=\frac{1}{\sqrt{L C}}$. For resonance to occur, the presence of both $L$ and $C$ elements in the circuit is a must. With only one of these ( $L$ or $C$ ) elements, there is no possibility of voltage cancellation and hence, no resonance is possible.
9. The power factor in a $R L C$ circuit is a measure of how close the circuit is to expending the maximum power.
10. In generators and motors, the roles of input and output are reversed. In a motor, electric energy is the input and mechanical energy is the output. In a generator, mechanical energy is the input and electric energy is the output. Both devices simply transform energy from one form to another.
11. A transformer (step-up) changes a low-voltage into a high-voltage. This does not violate the law of conservation of energy. The current is reduced by the same proportion.
Exercises
7.1 A $100 \Omega$ resistor is connected to a $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ac supply.
(a) What is the rms value of current in the circuit?
(b) What is the net power consumed over a full cycle?
Show Answer
Answer
Resistance of the resistor, $R=100 \Omega$
Supply voltage, $V=220 \mathrm{~V}$
Frequency, $v=50 \mathrm{~Hz}$
(a) The rms value of current in the circuit is given as:
$$ \begin{aligned} I & =\frac{V}{R} \\ & =\frac{220}{100}=2.20 \mathrm{~A} \end{aligned} $$
(b) The net power consumed over a full cycle is given as:
$$ P=V I $$
$=220 \times 2.2=484 \mathrm{~W}$
7.2 (a) The peak voltage of an ac supply is $300 \mathrm{~V}$. What is the rms voltage?
(b) The rms value of current in an ac circuit is $10 \mathrm{~A}$. What is the peak current?
Show Answer
Answer
(a) Peak voltage of the ac supply, $V_{0}=300 \mathrm{~V}$
Rms voltage is given as:
$$ \begin{aligned} V & =\frac{V_{0}}{\sqrt{2}} \\ & =\frac{300}{\sqrt{2}}=212.1 \mathrm{~V} \end{aligned} $$
(b) Therms value of current is given as:
$I=10 \mathrm{~A}$
Now, peak current is given as:
$$ \begin{aligned} I_{0} & =\sqrt{2} I \\ & =10 \sqrt{2}=14.1 \mathrm{~A} \end{aligned} $$
7.3 A $44 \mathrm{mH}$ inductor is connected to $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ac supply. Determine the rms value of the current in the circuit.
Show Answer
Answer
Inductance of inductor, $L=44 \mathrm{mH}=44 \times 10^{-3} \mathrm{H}$
Supply voltage, $V=220 \mathrm{~V}$
Frequency, $v=50 \mathrm{~Hz}$
Angular frequency, $\omega=2 \pi v$
Inductive reactance, $X_{\mathrm{L}}=\omega L=2 \pi \nu L=2 \pi \times 50 \times 44 \times 10^{-3} \Omega$
Rms value of current is given as:
$$ \begin{aligned} I & =\frac{v}{X_{\mathrm{L}}} \\ & =\frac{220}{2 \pi \times 50 \times 44 \times 10^{-3}}=15.92 \mathrm{~A} \end{aligned} $$
Hence, the rms value of current in the circuit is $15.92 \mathrm{~A}$.
7.4 A $60 \mu \mathrm{F}$ capacitor is connected to a $110 \mathrm{~V}, 60 \mathrm{~Hz}$ ac supply. Determine the rms value of the current in the circuit.
Show Answer
Answer
Capacitance of capacitor, $C=60 \mu \mathrm{F}=60 \times 10^{-6} \mathrm{~F}$
Supply voltage, $V=110 \mathrm{~V}$
Frequency, $v=60 \mathrm{~Hz}$
Angular frequency, $\omega=2 \pi v$
Capacitive reactance $X_{\mathrm{c}}=\frac{1}{\omega C}$
$=\frac{1}{2 \pi v C}$
$=\frac{1}{2 \times 3.14 \times 60 \times 60 \times 10^{-6}} \Omega^{-1}$
Rms value of current is given as:
$$ \begin{aligned} I & =\frac{v}{X_{\mathrm{c}}} \\ & =110 \times 2 \times 3.14 \times 60 \times 10^{-6} \times 60=2.49 \mathrm{~A} \end{aligned} $$
Hence, the rms value of current is $2.49 \mathrm{~A}$.
7.5 In Exercises 7.3 and 7.4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.
Show Answer
Answer
In the inductive circuit,
Rms value of current, $I=15.92 \mathrm{~A}$
Rms value of voltage, $V=220 \mathrm{~V}$
Hence, the net power absorbed can be obtained by the relation,
$P=V I \cos \Phi$
Where,
$\Phi=$ Phase difference between $V$ and $I$
For a pure inductive circuit, the phase difference between alternating voltage and current is $90^{\circ}$ i.e., $\Phi=90^{\circ}$.
Hence, $P=0$ i.e., the net power is zero.
In the capacitive circuit,
Rms value of current, $I=2.49$ A
Rms value of voltage, $V=110 \mathrm{~V}$
Hence, the net power absorbed can ve obtained as:
$P=V I \operatorname{Cos} \Phi$
For a pure capacitive circuit, the phase difference between alternating voltage and current is $90^{\circ}$ i.e., $\Phi=90^{\circ}$.
Hence, $P=0$ i.e., the net power is zero.
7.6 A charged $30 \mu \mathrm{F}$ capacitor is connected to a $27 \mathrm{mH}$ inductor. What is the angular frequency of free oscillations of the circuit?
Show Answer
Answer
Capacitance, $C=30 \mu \mathrm{F}=30 \times 10^{-6} \mathrm{~F}$
Inductance, $L=27 \mathrm{mH}=27 \times 10^{-3} \mathrm{H}$
Angular frequency is given as:
$$ \begin{aligned} \omega_{r} & =\frac{1}{\sqrt{L C}} \\ & =\frac{1}{\sqrt{27 \times 10^{-3} \times 30 \times 10^{-6}}}=\frac{1}{9 \times 10^{-4}}=1.11 \times 10^{3} \mathrm{rad} / \mathrm{s} \end{aligned} $$
Hence, the angular frequency of free oscillations of the circuit is $1.11 \times 10^{3} \mathrm{rad} / \mathrm{s}$.
7.7 A series $L C R$ circuit with $R=20 \Omega, L=1.5 \mathrm{H}$ and $C=35 \mu \mathrm{F}$ is connected to a variable-frequency $200 \mathrm{~V}$ ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
Show Answer
Answer
At resonance, the frequency of the supply power equals the natural frequency of the given LCR circuit.
Resistance, $R=20 \Omega$
Inductance, $L=1.5 \mathrm{H}$
Capacitance, $C=35 \mu \mathrm{F}=30 \times 10^{-6} \mathrm{~F}$
AC supply voltage to the $L C R$ circuit, $V=200 \mathrm{~V}$
Impedance of the circuit is given by the relation,
$Z=\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}$
At resonance, $\omega L=\frac{1}{\omega C}$
$\therefore Z=R=20 \Omega$
Current in the circuit can be calculated as:
$$ \begin{aligned} I & =\frac{V}{Z} \\ & =\frac{200}{20}=10 \mathrm{~A} \end{aligned} $$
Hence, the average power transferred to the circuit in one complete cycle $=V I$
$=200 \times 10=2000 \mathrm{~W}$.
7.8 Figure 7.17 shows a series $L C R$ circuit connected to a variable frequency $230 \mathrm{~V}$ source. $L=5.0 \mathrm{H}, C=80 \mu \mathrm{F}, R=40 \Omega$.
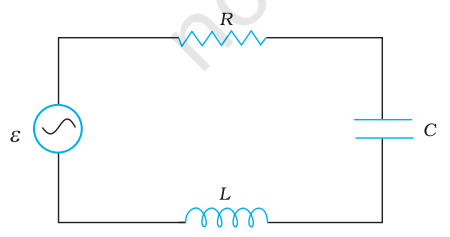
FIGURE 7.17
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the $L C$ combination is zero at the resonating frequency.
Show Answer
Answer
Inductance of the inductor, $L=5.0 \mathrm{H}$ Capacitance of the capacitor, $C=80 \mu \mathrm{H}=80 \times 10^{-6} \mathrm{~F}$ Resistance of the resistor, $R=40 \Omega$ Potential of the variable voltage source, $V=230 \mathrm{~V}$ (a) Resonance angular frequency is given as: $$ \begin{aligned} \omega_R & =\frac{1}{\sqrt{L C}} \ & =\frac{1}{\sqrt{5 \times 80 \times 10^{-6}}}=\frac{10^3}{20}=50 \mathrm{rad} / \mathrm{s} \end{aligned} $$
Hence, the circuit will come in resonance for a source frequency of $50 \mathrm{rad} / \mathrm{s}$.
(b) Impedance of the circuit is given by the relation, $$ Z=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2} $$
At resonance, $$ \begin{aligned} & \omega L=\frac{1}{\omega C} \ & \therefore Z=R=40 \Omega \end{aligned} $$
Amplitude of the current at the resonating frequency is given as: $I_0=\frac{V_0}{Z}$ Where, $$ \begin{aligned} V_0 & =\text { Peak voltage } \ & =\sqrt{2} \mathrm{~V} \ \therefore I_0 & =\frac{\sqrt{2} \mathrm{~V}}{Z} \ & =\frac{\sqrt{2} \times 230}{40}=8.13 \mathrm{~A} \end{aligned} $$
Hence, at resonance, the impedance of the circuit is $40 \Omega$ and the amplitude of the current is $8.13 \mathrm{~A}$.
(c) Rms potential drop across the inductor, $$ \left(V_L\right)_{\text {rms }}=I \times \omega_R L $$
Where, $I=$ rms current $$ \begin{aligned} & =\frac{I_0}{\sqrt{2}}=\frac{\sqrt{2} V}{\sqrt{2} Z}=\frac{230}{40} \mathrm{~A} \ & \therefore\left(V_L\right)_{\text {rms }}=\frac{230}{40} \times 50 \times 5=1437.5 \mathrm{~V} \end{aligned} $$
Potential drop across the capacitor, $$ \begin{aligned} \left(V_c\right)_{\mathrm{ms}} & =I \times \frac{1}{\omega_R C} \ & =\frac{230}{40} \times \frac{1}{50 \times 80 \times 10^{-6}}=1437.5 \mathrm{~V} \end{aligned} $$
Potential drop across the resistor, $$ \begin{aligned} & \left(V_R\right)_{\mathrm{rms}}=I R \ & =\frac{230}{40} \times 40=230 \mathrm{~V} \end{aligned} $$
Potential drop across the LC combination, $$ V_{L C}=I\left(\omega_R L-\frac{1}{\omega_R C}\right) $$
At resonance, $\omega_R L=\frac{1}{\omega_R C}$ $$ \therefore V_{L C}=0 $$
Hence, it is proved that the potential drop across the $L C$ combination is zero at resonating frequency.
7.1 भूमिका
अब तक हमने दिष्टधारा $(\mathrm{dc})$ स्रोतों एवं दिष्टधारा स्रोतों से युक्त परिपथों पर विचार किया है। समय के साथ इन धाराओं की दिशा में परिवर्तन नहीं होता। तथापि, समय के साथ परिवर्तित होने वाली धाराओं और वोल्टताओं का मिलना एक आम बात है। हमारे घरों एवं दफ्तरों में पाया जाने वाला मुख्य विद्युत प्रदाय (electric mains supply) एक ऐसी ही वोल्टता का स्रोत है जो समय के साथ ज्या फलन (sine function) की भाँति परिवर्तित होता है। ऐसी वोल्टता को प्रत्यावर्ती (ac) वोल्टता तथा किसी परिपथ में इसके द्वारा अचालित धारा को प्रत्यावर्ती धारा (ac धारा)* कहते हैं। आजकल जिन वैद्युत युक्तियों का हम उपयोग करते हैं उनमें से अधिकांश के लिए $\mathrm{ac}$ वोल्टता की ही आवश्यकता होती है। इसका मुख्य कारण यह है कि अधिकांश विद्युत कंपनियों द्वारा बेची जा रही विद्युत ऊर्जा प्रत्यावर्ती धारा के रूप में ही संप्रेषित एवं वितरित होती है। dc पर $\mathrm{ac}$ के उपयोग को वरीयता दिए जाने का मुख्य कारण यह है कि $\mathrm{ac}$ वोल्टताओं को ट्रांसफॉर्मरों द्वारा आसानी से एवं दक्षता के साथ एक वोल्टता से दूसरी वोल्टता में बदला जा सकता है। इसके अतिरिक्त $a c$ के रूप में लंबी दूरियों तक वैद्युत ऊर्जा का संप्रेषण भी अपेक्षाकृत कम खर्चीला होता है। प्रत्यावर्ती धारा परिपथ ऐसे अभिलक्षण प्रदर्शित करता है जिनका उपयोग दैनिक जीवन में काम आने वाली अनेक युक्तियों में किया जाता है। उदाहरणार्थ, जब हम अपने रेडियो को अपने मनपसंद स्टेशन से समस्वरित करते हैं तो $a c$ परिपथों के एक विशिष्ट गुण का लाभ उठाते हैं जो उन अनेक गुणों में से एक है जिनका अध्ययन आप इस अध्याय में करेंगे।
- $\mathrm{ac}$ वोल्टता एवं $\mathrm{ac}$ धारा, ये वाक्यांश असंगत एवं अनुप्रयुक्त हैं, क्योंकि इनका शब्दिक अर्थ है क्रमशः ‘प्रत्यावर्ती धारा वोल्टता’ एवं ‘प्रत्यावर्ती धारा धारा’। तब भी संकेताक्षर ac समय के अनुसार सरल आवर्ती क्रम में परिवर्तित होने वाली वैद्युत राशि को व्यक्त करने के लिए इतनी सार्वभौमिक स्वीकृति पा चुका है कि इसके प्रयोग में हम प्रचलित परिपाटी का ही अनुसरण करेंगे। इसके अतिरिक्त, सामान्यतः प्रयुक्त होने वाले शब्द वोल्टता का अर्थ दो बिंदुओं के बीच विभवांतर होता है।
7.2 प्रतिरोधक पर प्रयुक्त ac वोल्टता

निकोला टेस्ला (1856 - 1943) सर्बिया-अमेरिका के वैज्ञानिक, आविष्कर्ता एवं प्रतिभावान व्यक्ति। चुंबकीय क्षेत्र को घुमाने का उनका विचार ही व्यावहारिक रूप में सब प्रत्यावर्ती धारा मशीनों का आधार बना जिसके कारण विद्युत शक्ति के युग में प्रवेश किया जा सका। अन्य वस्तुओं के अतिरिक्त, प्रेरण मोटर, ac शक्ति की बहुफेज़ प्रणाली; रेडियो, टेलीविजन तथा अन्य वैद्युत उपकरणों पर लगने वाली उच्च आवृत्ति प्रेरण कुंडली (टेस्ला कुंडली) का आविष्कार भी उन्होंने किया। चुंबकीय क्षेत्र के SI मात्रक का नाम उनके सम्मान में रखा गया है।
चित्र 7.1 में $\mathrm{ac}$ वोल्टता स्रोत $\varepsilon$ से जुड़ा प्रतिरोधक $R$ दर्शाया गया है। परिपथ आरेख में $\mathrm{ac}$ म्रोत का संकेत चि्न $\Theta$ है। यहाँ हम एक ऐसे स्रोत की बात कर रहे हैं जो अपने सिरों के बीच ज्यावक्रीय रूप में परिवर्तनशील विभवांतर उत्पन्न करता है, माना कि यह विभवांतर जिसे $\mathrm{ac}$ वोल्टता भी कहा जाता है, निम्नलिखित प्रकार से व्यक्त किया जाए
$$ \begin{equation*} v=v_{m} \sin \omega t \tag{7.1} \end{equation*} $$
यहाँ $v _{m}$ दोलायमान विभवांतर का आयाम एवं $\omega$ इसकी कोणीय आवृत्ति है।

चित्र 7.1 प्रतिरोधक पर प्रयुक्त $\mathrm{ac}$ वोल्टता।
प्रतिरोधक में प्रवाहित होने वाली धारा का मान प्राप्त करने के लिए हम चित्र 7.1 में दर्शाए गए परिपथ पर किरोफ का लूप नियम $\sum \varepsilon(t)=0$, (खण्ड 3.12 देखें) लागू करते हैं जिससे हमें प्राप्त होता है :
$v _{m} \sin \omega t=i R$
अथवा $i=\frac{v _{m}}{R} \sin \omega t$
चूँकि $R$ एक नियतांक है, हम इस समीकरण को इस प्रकार व्यक्त कर सकते हैं :
$$ \begin{equation*} i=i_{m} \sin \omega t \tag{7.2} \end{equation*} $$
यहाँ धारा आयाम $i _{m}$ के लिए सूत्र है :
$$ \begin{equation*} i_{m}=\frac{v_{m}}{R} \tag{7.3} \end{equation*} $$

चित्र 7.2 शुद्ध प्रतिरोधक में वोल्टता एवं धारा एक ही कला में हैं। निम्निष्ठ, शून्य तथा उच्चिष्ठ क्रमशः एक ही समय में बनते हैं। वाली माध्य शक्ति भी शून्य है, और विद्युत ऊर्जा का क्षय नहीं हो रहा है। जैसा कि आप
समीकरण (7.3) ओम का नियम है जो प्रतिरोधकों के प्रकरण में ac एवं $\mathrm{dc}$ दोनों प्रकार की वोल्टताओं के लिए समान रूप से लागू होता है। समीकरण (7.1) एवं समीकरण (7.2) द्वारा व्यक्त किसी शुद्ध प्रतिरोधक के सिरों के बीच लगाई गई वोल्टता एवं इसमें प्रवाहित होने वाली धारा को चित्र 7.2 में समय के फलन के रूप में आलेखित किया गया है। इस तथ्य पर विशेष ध्यान दीजिए कि $v$ एवं $i$ दोनों ही शून्य, न्यूनतम एवं अधिकतम मानों की स्थितियाँ साथ-साथ ही प्राप्त करती हैं। अतः स्पष्ट है कि वोल्टता एवं धारा एक दूसरे के साथ समान कला में हैं।
हम देखते हैं कि प्रयुक्त वोल्टता की भाँति ही धारा भी ज्या-वक्रीय रूप में परिवर्तित होती है और तदनुसार ही प्रत्येक चक्र में इसके धनात्मक एवं ऋणात्मक मान प्राप्त होते हैं। अतः एक संपूर्ण चक्र में तात्क्षणिक धारा मानों का योग शून्य होता है तथा माध्य धारा शून्य होती है। तथापि माध्य धारा शून्य है इस तथ्य का यह अर्थ नहीं है कि व्यय होने जानते हैं जूल $i^{2} R$ द्वारा व्यक्त होता है और $i^{2}$ (जो सदैव धनात्मक ही होता है चाहे $i$ धनात्मक हो या ऋणात्मक) पर निर्भर करता है, न कि $i$ पर। अतः जब किसी प्रतिरोधक से $\mathrm{ac}$ धारा प्रवाहित होती है तो जूल तापन एवं वैद्युत ऊर्जा का क्षय होता है।

जॉर्ज वेस्टिंगहाउस (1846 - 1914) दिष्टधारा की तुलना में प्रत्यावर्ती धारा के प्रमुख पक्षधर। अतः दिष्टधारा के समर्थक थॉमस अल्वा एडीसन से उनका सीधा संघर्ष हुआ। वेस्टिंगहाउस का पूर्ण विश्वास था कि प्रत्यावर्ती धारा प्रौद्योगिकी के हाथ में ही वैद्युतीय भविष्य की कुंजी है। उन्होंने अपने नाम वाली प्रसिद्ध कम्पनी की स्थापना की और निकोला टेस्ला एवं अन्य आविष्कारकों को प्रत्यावर्ती धारा मोटरों एवं उच्च वोल्टता पर विद्युत धारा के संप्रेषण संबंधी उपकरणों के विकास के लिए नियुक्त किया, जिससे बड़े पैमाने पर प्रकाश प्राप्त करने का मार्ग खुला।
प्रतिरोधकता के क्षयित होने वाली तात्क्षणिक शक्ति होती है
$$ \begin{equation*} p=i^{2} R=i _{m}^{2} R \sin ^{2} \omega t \tag{7.4} \end{equation*} $$
एक समय चक्र में $p$ का माध्य मान है*
$$ \begin{equation*} \bar{p}=<i^{2} R>=<i _{m}^{2} R \sin ^{2} \omega t> \tag{7.5 a} \end{equation*} $$
जहाँ किसी अक्षर के ऊपर लगी रेखा (यहाँ $p$ ) उसका माध्य मान निर्दिष्ट करती है एवं <…..> यह सूचित करता है कि कोष्ठक के अंदर की राशि का माध्य लिया गया है। चूँकि $i _{m}^{2}$ एवं $R$ नियत राशियाँ हैं
$$ \begin{equation*} \bar{p}=i _{m}^{2} R<\sin ^{2} \omega t> \tag{7.5 b} \end{equation*} $$
त्रिकोणमितीय सर्वसमिका $\sin ^{2} \omega t=(1 / 2)(1-\cos 2 \omega t)$, का उपयोग करने पर $<\sin ^{2} \omega t>=(1 / 2)(1-<\cos 2 \omega t>)$ और चूँकि $<\cos 2 \omega t>$ $=0$ **, इसीलिए
$$ <\sin ^{2} \omega t>=\frac{1}{2} $$
अतः,
$$ \begin{equation*} \bar{p}=\frac{1}{2} i _{m}^{2} R \tag{7.5 c} \end{equation*} $$
$\mathrm{ac}$ शक्ति को उसी रूप में व्यक्त करने के लिए जिसमें dc शक्ति $\left(P=i^{2} R\right)$ को व्यक्त किया जाता है धारा के एक विशिष्ट मान का उपयोग किया जाता है जिसे वर्ग माध्य मूल (rms) अथवा प्रभावी (effective) धारा (चित्र 7.3 ) कहते हैं और इसे $I _{r m s}$ अथवा $I$ द्वारा निर्दिष्ट किया जाता है।

चित्र 7.3 $\mathrm{rms}$ धारा $I$, शिखरधारा $i _{m}$ से सूत्र $I=i _{m} / \sqrt{2}=0.707 i _{m}$ द्वारा संबंधित है।
- किसी फलन $F(t)$ का समयावधि $T$ में माध्यमान ज्ञात करने के लिए सूत्र है $\langle F(t)\rangle=\frac{1}{T} \int _{0}^{T} F(t) \mathrm{d} t$
$<\cos 2 \omega t>=\frac{1}{T} \int _{0}^{T} \cos 2 \omega t \mathrm{~d} t=\frac{1}{T}\left[\frac{\sin 2 \omega t}{2 \omega}\right] _{0}^{T}=\frac{1}{2 \omega T}[\sin 2 \omega T-0]=0$
इसे इस प्रकार व्यक्त किया जाता है
$$ \begin{align*} I=\sqrt{\overline{i^{2}}} & =\sqrt{\frac{1}{2} i _{m}^{2}}=\frac{i _{m}}{\sqrt{2}} \\ & =0.707 I _{m} \tag{7.6} \end{align*} $$
$I$ के पदों में व्यक्त करें तो $P$ द्वारा निर्दिष्ट माध्य शक्ति
$$ \begin{equation*} P=\bar{p}=\frac{1}{2} i _{m}^{2} R=I^{2} R \tag{7.7} \end{equation*} $$
इसी प्रकार, rms वोल्टता अथवा प्रभावी वोल्टता को हम व्यक्त करते हैं :
$$ \begin{equation*} V=\frac{v _{m}}{\sqrt{2}}=0.707 v _{m} \tag{7.8} \end{equation*} $$
समीकरण (7.3) के आधार पर
$$ v_{m}=i_{m} R $$
अथवा, $\frac{v _{m}}{\sqrt{2}}=\frac{i _{m}}{\sqrt{2}} R$
अथवा,$V=I R$
समीकरण (7.9) $\mathrm{ac}$ धारा एवं $\mathrm{ac}$ वोल्टता के बीच संबंध बताती है जो $\mathrm{dc}$ में इन राशियों के संबंध के समान ही है। यह $\mathrm{rms}$ मानों की अवधारणा के लाभ दर्शाती है। rms मानों के पदों में, $\mathrm{ac}$ परिपथों के लिए शक्ति का समीकरण (7.7) एवं धारा तथा वोल्टता का संबंध वही है जो $\mathrm{dc}$ के लिए होता है।
परंपरा यह कि ac राशियों को उनके rms मानों के पदों में मापा और व्यक्त किया जाए। उदाहरणार्थ, घरेलू आपूर्ति में $220 \mathrm{~V}$ वोल्टता का $\mathrm{rms}$ मान है जिसका शिखर मान है
$$ v _{m}=\sqrt{2} V=(1.414)(220 \mathrm{~V})=311 \mathrm{~V} $$
वास्तव में, $I$ अथवा $\mathrm{rms}$ धारा उस dc धारा के समतुल्य है जो वही माध्य शक्ति ह्रास करेगी जो प्रत्यावर्ती धारा करती है। समीकरण (7.7) को निम्नलिखित रूप में भी प्रस्तुत कर सकते हैं-
$$ P=V^{2} / R=I V \quad(\text { चूँकि } V=I R) $$
उदाहरण 7.1 एक विद्युत बल्ब $220 \mathrm{~V}$ आपूर्ति पर $100 \mathrm{~W}$ शक्ति देने के लिए बनाया गया है। (a) बल्ब का प्रतिरोध; (b) स्रोत की शिखर वोल्टता एवं (c) बल्ब में प्रवाहित होने वाली rms धारा ज्ञात कीजिए।
हल
(a) दिया है $P=100 \mathrm{~W}$ एवं $V=220 \mathrm{~V}$ । बल्ब का प्रतिरोध है :
$$ R=\frac{V^{2}}{P}=\frac{(220 \mathrm{~V})^{2}}{100 \mathrm{~W}}=484 \Omega $$
(b) स्रोत की शिखर वोल्टता
$$ v _{m}=\sqrt{2} \mathrm{~V}=311 \mathrm{~V} $$
(c) चूँकि, $P=I V$
$$I=\frac{P}{V}=\frac{100 \mathrm{~W}}{220 \mathrm{~V}}=0.450 \mathrm{~A}$$
7.3 $\mathrm{ac}$ धारा एवं वोल्टता का घूर्णी सदिश द्वारा निरूपणकलासमंजक ( फेजर्स )
पिछले अनुभाग में हमने सीखा कि किसी प्रतिरोधक में प्रवाहित होने वाली धारा तथा $a c$ वोल्टता समान कला में रहते हैं। परन्तु प्रेरक, संधारित्र अथवा इनके संयोजन युक्त परिपथों में ऐसा नहीं होता $\mathrm{ac}$ परिपथ में धारा एवं वोल्टता के बीच कला संबंध दर्शाने के लिए हम फेजर्स की धारणा का उपयोग करते हैं। फेजर चित्र के उपयोग से $\mathrm{ac}$ परिपथ का विश्लेषण सरलतापूर्वक हो जाता है। फेजर* जैसा कि चित्र 7.4 में दर्शाया गया है, एक सदिश है जो मूल बिंदु के परितः कोणीय वेग $\omega$ से घूर्णन करता है। फेजर्स $\mathbf{V}$ एवं I के ऊर्ध्वाधर घटक ज्यावक्रीय रूप से परिवर्तनशील राशियाँ $v$ एवं $i$ निरूपित करते हैं। फेजर्स $\mathbf{V}$ एवं $\mathbf{I}$ के परिमाण इन दोलायमान राशियों के आयाम अथवा शिखरमान $v _{m}$ एवं $i _{m}$ निरूपित करते हैं। चित्र 7.4 (a) चित्र 7.1 के संगत किसी प्रतिरोधक के सिरों से जुड़ी $a c$ वोल्टता की, किसी क्षण $t _{1}$ पर, वोल्टता एवं धारा के फेजर्स और उनका पारस्परिक संबंध दर्शाता है। वोल्टता एवं धारा के ऊर्ध्वाधर अक्ष पर प्रक्षेप अर्थात $v _{m}$ $\sin \omega t$ एवं $i _{m} \sin \omega t$, क्रमशः, उस क्षण विशेष पर वोल्टता एवं धारा के मान निरूपित करते हैं। ज्यों-ज्यों वे आवृत्ति $\omega$ से घूर्णन करते हैं चित्र 7.4(b) में दर्शाए गए वक्र जैसे होते हैं।

चित्र 7.4 (a) चित्र 7.1 में दर्शाए गए परिपथ के लिए फेजर आरेख (b) $v$ एवं $i$ तथा $\omega t$ के बीच ग्राफ। है।
चित्र 7.4(a) से हम यह समझ सकते हैं कि प्रतिरोधक के लिए फेजर्स $\mathbf{V}$ एवं $\mathbf{I}$ एक ही दिशा में होते हैं। ऐसा हर समय होता है। इसका अर्थ है कि वोल्टता एवं धारा के बीच कला कोण शून्य होता है।
7.4 प्रेरक पर प्रयुक्त ac वोल्टता
चित्र 7.5 एक प्रेरक के सिरों पर लगा ac स्रोत दर्शाता है। प्राय: प्रेरक के लपेटों में लगे तार का अच्छा खासा प्रतिरोध होता है, लेकिन यहाँ हम यह मानेंगे कि इस प्रेरक का प्रतिरोध नगण्य है। अतः यह परिपथ विशुद्ध प्रेरणिक $\mathrm{ac}$ परिपथ है। माना कि स्रोत के सिरों के बीच वोल्टता $v=v _{m} \sin \omega t$ है क्योंकि परिपथ में कोई प्रतिरोधक नहीं है। किरखोफ लूप नियम $\sum \varepsilon(t)=0$, का उपयोग करने से
$$ \begin{equation*} v-L \frac{\mathrm{d} i}{\mathrm{~d} t}=0 \tag{7.10} \end{equation*} $$
यहाँ समीकरण का दूसरा पद प्रेरक में स्वप्रेरित फैराडे $\mathrm{emf}$ है, एवं $L$ प्रेरक का स्व-प्रेरकत्व है। ॠणात्मक चिन्न लेंज के नियम का अनुसरण करने से

चित्र 7.5 प्रेरक से जुड़ा एक $\mathrm{ac}$ स्रोत।
- यद्यपि ac परिपथ में वोल्टता एवं धारा को घूर्णन करते सदिशों-फेजर्स द्वारा निरूपित किया जाता है, अपने आप में वे सदिश नहीं हैं। वे अदिश राशियाँ हैं। होता यह है, कि आवर्ती रूप से परिवर्तित होते अदिशों की कलाएँ एवं आयाम गणितीय रूप से उसी प्रकार संयोजित होते हैं जैसे कि उन्हीं परिमाण एवं दिशाओं वाले घूर्णन सदिशों के प्रक्षेप। आवर्ती रूप से परिवर्तित होने वाली अदिश राशियों को, घूर्णन सदिशों द्वारा निरूपित करने से हम इन राशियों का संयोजन एक सरल विधि द्वारा, एक पहले से ही ज्ञात नियम का प्रयोग करके, कर सकते हैं।
समाविष्ट होता है (अध्याय 6)। समीकरण (7.1) एवं समीकरण (7.10) को संयोजित करने पर
$$ \begin{equation*} \frac{\mathrm{d} i}{\mathrm{~d} t}=\frac{v}{L}=\frac{v_{m}}{L} \sin \omega t \tag{7.11} \end{equation*} $$
समीकरण (7.11) में यह सन्निहित है कि धारा $i(t)$ के लिए समीकरण समय का ऐसा फलन होना चाहिए कि इसकी प्रवणता, $\mathrm{d} i / \mathrm{d} t$ एक ज्यावक्रीय रूप में परिवर्तनशील राशि हो जो स्रोत वोल्टता के साथ समान कला में रहती हो और जिसका आयाम $v _{m} / L$ द्वारा प्राप्त होता हो। धारा का मान प्राप्त करने के लिए, हम $\mathrm{d} i / \mathrm{d} t$ को समय के सापेक्ष समाकलित करते हैं,
$$ \int \frac{\mathrm{d} i}{\mathrm{~d} t} \mathrm{~d} t=\frac{v _{m}}{L} \int \sin (\omega t) \mathrm{d} t $$
इससे हमें प्राप्त होता है :
$$ i=-\frac{v _{m}}{\omega L} \cos (\omega t)+\text { नियतांक } $$
यहाँ समाकलन नियतांक की विमा, धारा की विमा होती है और यह समय पर निर्भर नहीं करती। चूँकि, स्रोत का emf शून्य के परितः सममितीय रूप से दोलन करता है; वह धारा, जो इसके कारण बहती है, भी सममितीय रूप से दोलन करती है। अतः न तो धारा का कोई नियत, न ही समय पर निर्भर करने वाला अवयव, अस्तित्व में आता है। इसलिए, समाकलन नियतांक का मान शून्य होता है।
$$ \begin{align*} & -\cos (\omega t)=\sin \left(\omega t-\frac{\pi}{2}\right) \text {, लिखें तो } \end{align*} $$
$$ \begin{align*} & i=i _{m} \sin \left(\omega t-\frac{\pi}{2}\right) \tag{7.12} \end{align*} $$
यहाँ $i _{m}=\frac{v _{m}}{\omega L}$ धारा का आयाम है। राशि $\omega L$ प्रतिरोध के सदृश है, इसे प्रेरकीय प्रतिघात कहा जाता है एवं इसे $X _{\mathrm{L}}$ द्वारा व्यक्त करते हैं।
$$ \begin{equation*} X _{L}=\omega L \tag{7.13} \end{equation*} $$
तब, धारा का आयाम है :
$$ \begin{equation*} i _{m}=\frac{v _{m}}{X _{L}} \tag{7.14} \end{equation*} $$
प्रेरकीय प्रतिघात की विमाएँ वही हैं तो प्रतिरोध की और इसका SI मात्रक ओम $(\Omega)$ है। प्रेरकीय प्रतिघात एक शुद्ध प्रेरणिक परिपथ में धारा को वैसे ही नियंत्रित करता है जैसे प्रतिरोध एक शुद्ध प्रतिरोधक परिपथ में। प्रेरकीय प्रतिघात, प्रेरकत्व एवं धारा की आवृत्ति के अनुक्रमानुपाती होता है।
स्रोत वोल्टता एवं प्रेरक में प्रवाहित होने वाली धारा के समीकरण (7.1) एवं (7.12) की तुलना से यह ज्ञात होता है कि धारा वोल्टता से $\pi / 2$ अथवा $(1 / 4)$ चक्र पीछे रहती है। चित्र 7.6 (a) प्रस्तुत प्रकरण के $t _{1}$ क्षण पर, वोल्टता एवं धारा फेजर्स दर्शाता है। धारा फेजर $\mathbf{I}$ वोल्टता फेजर $\mathbf{V}$ से $\pi / 2$ पीछे है। जब उन्हें $\omega$ आवृत्ति से वामावर्त दिशा में घूर्णन कराते हैं तो ये वोल्टता एवं धारा जनित करते हैं जो क्रमशः समीकरण (7.1) एवं (7.12) द्वारा व्यक्त की जाती है और जिसे चित्र 7.6 (b) में दर्शाया गया है।

चित्र 7.6 (a) चित्र 7.5 में दर्शाए गए परिपथ का फेजर आरेख (b) $v$ एवं $i$ तथा $\omega t$ के बीच ग्राफ़।
हम देखते हैं कि धारा, वोल्टता की अपेक्षा चौथाई आवर्त काल $\left[\frac{T}{4}=\frac{\pi / 2}{\omega}\right]$ के पश्चात अपने अधिकतम मान को प्राप्त करती है। आपने देखा कि एक प्रेरक में प्रतिघात होता है जो धारा को उसी प्रकार नियंत्रित करता है जैसे $\mathrm{dc}$ परिपथ में प्रतिरोध करता है। पर, क्या प्रतिरोध की तरह ही इसमें भी शक्ति व्यय होती है? आइए, इसका पता लगाने का प्रयास करें।
प्रेरक को आपूर्त तात्क्षणिक शक्ति
$$ \begin{aligned} p_{L}=i v & =i_{m} \sin \omega t-\frac{\pi}{2} \times v_{m} \sin (\omega t) \end{aligned} $$
$$ \begin{aligned} & =-i_{m} v_{m} \cos (\omega t) \sin (\omega t) \\ & =-\frac{i_{m} v_{m}}{2} \sin (2 \omega t) \end{aligned} $$
अतः एक पूरे चक्र में माध्य शक्ति
$$ \begin{aligned} P _{\mathrm{L}} & =\left\langle-\frac{i _{m} v _{m}}{2} \sin (2 \omega t)\right\rangle \end{aligned} $$
$$ \begin{aligned} & =-\frac{i _{m} v _{m}}{2}\langle\sin (2 \omega t)\rangle=0 \end{aligned} $$
क्योंकि, एक पूरे चक्र में $\sin (2 \omega t)$ का माध्य शून्य होता है
इसलिए एक पूरे चक्र में किसी प्रेरक को आपूर्त माध्य शक्ति भी शून्य होती है।
उदाहरण 7.2 $25 .0 \mathrm{mH}$ का एक शुद्ध प्रेरक $220 \mathrm{~V}$ के एक स्रोत से जुड़ा है। यदि स्रोत की आवृत्ति $50 \mathrm{~Hz}$ हो तो परिपथ का प्रेरकीय प्रतिघात एवं $\mathrm{rms}$ धारा ज्ञात कीजिए।
हल प्रेरकीय प्रतिघात
$$ \begin{aligned} X _{L} & =2 \pi v L=2 \times 3.14 \times 50 \times 25 \times 10^{-3} \Omega \\ & =7.85 \Omega \end{aligned} $$
परिपथ में $\mathrm{rms}$ धारा
$$ I=\frac{V}{X _{L}}=\frac{220 \mathrm{~V}}{7.85 \Omega}=28 \mathrm{~A} $$
7.5 संधारित्र पर प्रयुक्त ac वोल्टता
चित्र 7.7 में एक संधारित्रीय $\mathrm{ac}$ परिपथ दर्शाया गया है जिसमें केवल एक संधारित्र एक ऐसे $\mathrm{ac}$ स्रोत $\varepsilon$ से जुड़ा है जो वोल्टता $v=v _{m} \sin \omega t$ प्रदान करता है।

चित्र 7.7 एक संधारित्र से जुड़ी $\mathrm{ac}$ वोल्टता।
जब dc परिपथ में वोल्टता स्रोत से किसी संधारित्र को जोड़ा जाता है तो इसमें धारा, उस अल्पकाल के लिए ही प्रवाहित होती है जो संधारित्र की प्लेटों पर एकत्रित होता है, उनके बीच विभवांतर बढ़ता है, जो धारा का विरोध करता है। अर्थात $\mathrm{dc}$ परिपथ में ज्यों-ज्यों संधारित्र आवेशित होता है यह परिपथ धारा को सीमित करता है अथवा उसके प्रवाह का विरोध करता है। जब संधारित्र पूरी तरह आवेशित हो जाता है तो परिपथ में धारा गिर कर शून्य हो जाती है।
जब संधारित्र को $\mathrm{ac}$ स्रोत से जोड़ा जाता है, जैसा कि चित्र 7.7 में दर्शाया गया है तो यह धारा को नियंत्रित तो करता है, पर आवेश के प्रवाह को पूरी तरह रोकता नहीं है। क्योंकि धारा प्रत्येक अर्द्ध चक्र में प्रत्यावर्तित होती है संधारित्र भी एकांतर क्रम में आवेशित एवं अनावेशित होता है। माना कि किसी क्षण $t$ पर संधारित्र पर आवेश $q$ है। तो संधारित्र के सिरों के बीच तात्क्षणिक वोल्टता है,
$$ \begin{equation*} v=\frac{q}{C} \tag{7.15} \end{equation*} $$
किरखोफ के लूप नियम के अनुसार, स्रोत एवं संधारित्र के सिरों के बीच वोल्टताएँ समान हैं, अतः
$$ v _{m} \sin \omega t=\frac{q}{C} $$
धारा का मान ज्ञात करने के लिए हम संबंध $i=\frac{\mathrm{d} q}{\mathrm{~d} t}$ का उपयोग करते हैं
$$ i=\frac{\mathrm{d}}{\mathrm{d} t}\left(v _{m} C \sin \omega t\right)=\omega C v _{m} \cos (\omega t) $$
संबंध, $\cos (\omega t)=\sin \left(\omega t+\frac{\pi}{2}\right)$, का उपयोग करने से हम पाते हैं,
$$ \begin{equation*} i=i _{m} \sin \left(\omega t+\frac{\pi}{2}\right) \tag{7.16} \end{equation*} $$
यहाँ, दोलायमान धारा का आयाम $i _{m}=\omega C v _{m}$ है। इसको हम
$$ i _{m}=\frac{v _{m}}{(1 / \omega C)} $$
के रूप में लिखें और विशुद्ध प्रतिरोधकीय परिपथ के तदनुरूपी सूत्र $i _{m}=v _{m} / R$ से तुलना करें तो हम पाते हें कि $(1 / \omega C)$ की भूमिका प्रतिरोध जैसी ही है। इसको संधारित्र प्रतिघात कहते हैं और $X _{c}$ से निरूपित करते हैं।
$$ \begin{equation*} X _{c}=1 / \omega C \tag{7.17} \end{equation*} $$
अतः धारा का आयाम है,
$$ \begin{equation*} i _{m}=\frac{v _{m}}{X _{C}} \tag{7.18} \end{equation*} $$
संधारित्रीय प्रतिघात की विमाएँ वही हैं जो प्रतिरोध की और इसका SI मात्रक ओम $(\Omega)$ है। संधारित्रीय प्रतिघात उसी प्रकार विशुद्ध संधारित्रीय परिपथ में धारा को नियंत्रित करता है जैसे विशुद्ध प्रतिरोधकीय परिपथ में प्रतिरोध, परंतु इसका मान आवृत्ति एवं धारिता के व्युत्क्रमानुपाती होता है।

चित्र 7.8 (a) चित्र 7.7 में दर्शाए गए परिपथ का फेजर आरेख (b) $v$ एवं $i$ का समय के सापेक्ष ग्राफ़।
समीकरण (7.16) की स्रोत वोल्टता की समीकरण (7.1) से तुलना करने पर हम पाते हैं कि धारा, वोल्टता से $\pi / 2$ अग्रगामी होती है। चित्र 7.8 (a) किसी क्षण $t _{1}$ पर फेजर आरेख दर्शाता है। यहाँ धारा फेजर $\mathbf{I}$, वोल्टता फेजर $\mathbf{V}$ से $\pi / 2$ कोण अग्रगामी है जब वे वामावर्त घूर्णन करते हैं। चित्र 7.8 (b), वोल्टता एवं धारा में समय के साथ होने वाला परिवर्तन दर्शाता है। हम देखते हैं कि धारा, वोल्टता की तुलना में चौथाई समयकाल पहले अधिकतम मान ग्रहण करती है।
संधारित्र को आपूर्त तात्कणिक शक्ति, $$ \begin{align*} p _{c} & =i v=i _{m} \cos (\omega t) v _{m} \sin (\omega t) \\ & =i _{m} v _{m} \cos (\omega t) \sin (\omega t) \\ & =\frac{i _{m} v _{m}}{2} \sin (2 \omega t) \tag{7.19} \end{align*} $$
अतः संधारित्र के प्रकरण में, माध्य शक्ति
$$ \overline{\mathrm{P}} _{C}=\left\langle\frac{i _{m} v _{m}}{2} \sin (2 \omega t)\right\rangle=\frac{i _{m} v _{m}}{2}\langle\sin (2 \omega t)\rangle=0 $$
क्योंकि एक पूर्ण चक्र पर $<\sin (2 \omega t)>=0$
इस प्रकार हम देखते हैं कि प्रेरक के प्रकरण में धारा, वोल्टता से $\pi / 2$ कोण पश्चगामी एवं संधारित्र के प्रकरण में धारा, वोल्टता से $\pi / 2$ कोण अग्रगामी होती है।
उदाहरण 7.3 एक लैंप किसी संधारित्र के साथ श्रेणीक्रम में जुड़ा है। dc एवं $\mathrm{ac}$ संयोजनों के लिए अपने प्रेक्षणों की प्रागुक्ति कीजिए। प्रत्येक प्रकरण में बताइए कि संधारित्र की धारिता कम करने का क्या प्रभाव होगा?
हल जब संधारित्र के साथ किसी $\mathrm{dc}$ स्रोत को जोड़ते हैं तो संधारित्र आवेशित होता है और उसके पूर्ण आवेशन के बाद परिपथ में कोई धारा प्रवाहित नहीं होती और लैंप प्रकाशित नहीं होता है। इस मामले में $C$ को कम करने से कोई परिवर्तन नहीं आएगा। ac स्रोत के साथ, संधारित्र $(1 / \omega C)$ संधारित्रीय प्रतिघात लगाता है और परिपथ में धारा प्रवाहित होती है। परिणामतः लैंप प्रकाश देगा। $C$ को कम करने से प्रतिघात बढ़ेगा और लैंप पहले की तुलना में दीप्ति से प्रकाशित होगा।
उदाहरण 7.4 $15 .0 \mu \mathrm{F}$ का एक संधारित्र, $220 \mathrm{~V}, 50 \mathrm{~Hz}$ स्रोत से जोड़ा गया है। परिपथ का संधारित्रीय प्रतिघात और इसमें प्रवाहित होने वाली ( $\mathrm{rms}$ एवं शिखर) धारा का मान बताइए। यदि आवृत्ति को दोगुना कर दिया जाए तो संधारित्रीय प्रतिघात और धारा के मान पर क्या प्रभाव होगा?
हल संधारित्रीय प्रतिघात है,
$$ X _{C}=\frac{1}{2 \pi v C}=\frac{1}{2 \pi(50 \mathrm{~Hz})\left(15.0 \times 10^{-6} \mathrm{~F}\right)}=212 \Omega $$
$\mathrm{rms}$ धारा है
$$ I=\frac{V}{X _{C}}=\frac{220 \mathrm{~V}}{212 \Omega}=1.04 \mathrm{~A} $$
शिखर धारा है
$$ i _{m}=\sqrt{2} I=(1.41)(1.04 \mathrm{~A})=1.47 \mathrm{~A} $$
यह धारा $+1.47 \mathrm{~A}$ एवं $-1.47 \mathrm{~A}$ के बीच दोलन करती है और वोल्टता से $\pi / 2$ कोण अग्रगामी होती है।
यदि आवृत्ति दोगुनी हो जाए तो संधारित्रीय प्रतिघात आधा रह जाता है, परिणामतः धारा दोगुनी हो जाती है।
उदाहरण 7.5 एक प्रकाश बल्ब और एक सरल कुंडली प्रेरक, एक कुंजी सहित, चित्र में दर्शाए अनुसार, एक $\mathrm{ac}$ स्रोत से जोड़े गए हैं। स्विच को बंद कर दिया गया है और कुछ समय पश्चात एक लोहे की छड़ प्रेरक कुंडली के अंदर प्रविष्ट कराई जाती है।

चित्र 7.9
छड़ को प्रविष्ट कराते समय प्रकाश बल्ब की चमक (a) बढ़ती है (b) घटती है (c) अपरिवर्तित रहती है। कारण सहित उत्तर दीजिए।
हल जैसे-जैसे लोहे की छड़ कुंडली में प्रवेश करती है कुंडली के अंदर का चुंबकीय क्षेत्र इसे चुंबकित कर देता है जिससे कुंडली के अंदर चुंबकीय क्षेत्र बढ़ जाता है। अतः कुंडली का प्रेरकत्व बढ़ जाता है। परिणामतः कुंडली का प्रेरकीय प्रतिघात बढ़ जाता है। इस प्रकार प्रयुक्त $\mathrm{ac}$ वोल्टता का अधिकांश भाग प्रेरक के सिरों के बीच प्रभावी हो जाता है और बल्ब के सिरों के बीच वोल्टता कम रह जाती है। अतः बल्ब की दीप्ति कम हो जाती है।
7.6 श्रेणीबद्ध LCR परिपथ पर प्रयुक्त ac वोल्टता
चित्र 7.10, $\mathrm{ac}$ स्रोत $\varepsilon$ से जुड़ा श्रेणीबद्ध $\mathrm{LCR}$ परिपथ दर्शाता है। पहले की ही भाँति हम $\mathrm{ac}$ स्रोत की वोल्टता $v=v _{m} \sin \omega t$ लेते हैं।

चित्र 7.10 किसी $\mathrm{ac}$ स्रोत से संयोजित श्रेणीबद्ध LCR परिपथ।
यदि संधारित्र पर आवेश $q$ एवं किसी क्षण $t$ पर परिपथ में प्रवाहित धारा $i$ है तो किरोफ़ पाश नियम से
$$ \begin{equation*} L \frac{\mathrm{d} i}{\mathrm{~d} t}+i R+\frac{q}{C}=v \tag{7.20} \end{equation*} $$
हम तात्क्षणिक धारा $i$ और प्रयुक्त प्रत्यावर्ती वोल्टता $v$ के साथ इसका कला संबंध ज्ञात करना चाहते हैं। हम इस समस्या को हल करने के लिए दो विधियों का उपयोग करेंगे। पहली विधि में हम फेजर्स तकनीक का उपयोग करेंगे और दूसरी विधि में हम समीकरण (7.20) को विश्लेषणात्मक रूप से हल करके $i$ की कालाश्रितता प्राप्त करेंगे।
7.6.1 फेजर आरेख द्वारा हल
चित्र 7.10 में दर्शाए गए परिपथ में प्रतिरोधक, प्रेरक एवं संधारित्र श्रेणीक्रम में जुड़े हैं। अतः किसी क्षण विशेष पर परिपथ के हर घटक में $\mathrm{ac}$ धारा, उसके आयाम एवं कला समान हैं। माना कि
$$ \begin{equation*} i=i _{m} \sin (\omega t+\phi) \tag{7.21} \end{equation*} $$
यहाँ $\phi$ स्रोत की वोल्टता और परिपथ में प्रवाहित होने वाली धारा में कला-अंतर है। पिछले अनुभागों में हमने जो सीखा है उसके आधार पर हम वर्तमान प्रकरण का एक फेजर आरेख बनाएँगे।
मान लीजिए कि समीकरण (7.21) द्वारा प्रदत्त परिपथ की धारा को फेजर $\mathbf{I}$ द्वारा व्यक्त करें। और प्रेरक, प्रतिरोधक, संधारित्र एवं स्रोत के सिरों के बीच वोल्टताओं को क्रमशः $\mathrm{V} _{\mathrm{L}}, \mathrm{V} _{\mathrm{R}}, \mathrm{V} _{\mathrm{C}}$, एवं $\mathbf{V}$ से निरूपित करें तो पिछले अनुभाग से हम जानते हैं कि $\mathrm{V} _{\mathrm{R}}, \mathbf{I}$ के समातर है, $\mathrm{V} _{\mathrm{C}}$ धारा $I$ से $\pi / 2$ रेडियन पीछे है तथा $\mathbf{V} _{\mathbf{L}}, \mathbf{I}$ से $\pi / 2$ रेडियन आगे है। चित्र 7.11 (a) में $\mathbf{V} _{\mathbf{L}}, \mathbf{V} _{\mathbf{R}}, \mathbf{V} _{\mathbf{C}}$ एवं $\mathbf{I}$ को समुचित कला संबंधों के साथ दर्शाया गया है।
इन फेजर्स की लंबाई अर्थात $\mathbf{V} _{\mathbf{R}}, \mathbf{V} _{\mathbf{C}}$ एवं $\mathbf{V} _{\mathbf{L}}$ के आयाम हैं :
$$ \begin{equation*} v _{R m}=i _{m} R, v _{C m}=i _{m} X _{C}, v _{L m}=i _{m} X _{L} \tag{7.22} \end{equation*} $$
परिपथ के लिए वोल्टता समीकरण (7.20) को इस प्रकार लिखा जा सकता है
$$ \begin{equation*} v _{\mathrm{L}}+v _{\mathrm{R}}+v _{\mathrm{C}}=v \tag{7.23} \end{equation*} $$
वह फेजर संबंध जिसके ऊर्ध्वाधर घटकों द्वारा उपरोक्त समीकरण बनती है, वह है
$$ \begin{equation*} \mathbf{V} _{\mathbf{L}}+\mathbf{V} _{\mathbf{R}}+\mathbf{V} _{\mathbf{C}}=\mathbf{V} \tag{7.24} \end{equation*} $$

चित्र 7.11 (a) फेजर्स $\mathrm{V} _{\mathrm{L}}, \mathrm{V} _{\mathrm{R}}, \mathbf{V} _{\mathrm{C}}$, एवं $I$ के बीच पारस्परिक संबंध (b) फेजर्स $\mathrm{V} _{\mathrm{L}}, \mathbf{V} _{\mathrm{R}}$, एवं $\left(\mathrm{V} _{\mathrm{L}}+\mathbf{V} _{\mathrm{C}}\right)$ के बीच 7.10 में दर्शाए गए परिपथ के लिए संबंध।
इस संबंध को चित्र 7.11 (b) में प्रस्तुत किया गया है। चूँकि, $\mathrm{V} _{\mathrm{C}}$ एवं $\mathrm{v} _{\mathrm{L}}$ सदैव एक ही सरल रेखा में और एक दूसरे की विपरीत दिशाओं में होते हैं, उनको एक एकल फेजर $\left(\mathbf{V} _{\mathbf{C}}+\mathbf{V} _{\mathbf{L}}\right)$ के रूप में संयोजित किया जा सकता है जिसका परिमाण $\left|v _{C m}-v _{L m}\right|$ होता है। चूँकि $\mathbf{V}$ उस समकोण त्रिभुज के कर्ण से निरूपित किया गया है जिसकी भुजाएँ $\mathbf{V} _{\mathbf{R}}$ एवं $\left(\mathbf{V} _{\mathbf{C}}+\mathbf{V} _{\mathbf{L}}\right)$ हैं, पाइथागोरस प्रमेय द्वारा,
$$ v _{m}^{2}=v _{R m}^{2}+\left(v _{C m}-v _{L m}\right)^{2} $$
समीकरण (7.22) से $v _{R m}, v _{C m}$, एवं $v _{L m}$ के मान प्रत्येक समीकरण में रखने पर
$$ \begin{aligned} v _{m}^{2} & =\left(i _{m} R\right)^{2}+\left(i _{m} X _{C}-i _{m} X _{L}\right)^{2} \\ & =i _{m}^{2}\left[R^{2}+\left(X _{C}-X _{L}\right)^{2}\right] \end{aligned} $$
अथवा, $$ \begin{equation*} i_{m}=\frac{v_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}} \tag{7.25a} \end{equation*} $$
किसी परिपथ में प्रतिरोध से समतुल्यता के आधार पर हम $\mathrm{ac}$ परिपथ के लिए प्रतिबाधा, $Z$ पद को उपयोग में लाएँ तो
$$ \begin{equation*} i _{m}=\frac{v _{m}}{Z} \tag{7.25b} \end{equation*} $$
यहाँ
$$ \begin{equation*} Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}} \tag{7.26} \end{equation*} $$

चित्र 7.12 प्रतिबाधा आरेख।
चूँकि फेजर $I$ सदैव फेजर $V _{R}$ के समांतर होता है, कला कोण $\phi \mathbf{V} _{\mathbf{R}}$ एवं $\mathbf{V}$ के बीच बना कोण है और चित्र 7.12 के आधार पर इसका मान ज्ञात किया जा सकता है
$\tan \phi=\frac{v _{C m}-v _{L m}}{v _{R m}}$
समीकरण (7.22) का उपयोग करने पर,
$\tan \phi=\frac{X _{C}-X _{L}}{R}$ {7.27}
समीकरणों (7.26) एवं (7.27) का ग्राफीय निरूपण चित्र (7.12) में प्रस्तुत किया गया है। यह प्रतिबाधा आरेख कहलाता है। यह एक समकोण त्रिभुज है जिसका कर्ण $Z$ है।
समीकरण 7.25(a) धारा का आयाम बताती है एवं समीकरण (7.27) से कलाकोण का मान प्राप्त होता है। इनके साथ मिलकर समीकरण (7.21) पूर्णतः निर्दिष्ट हो जाती है। यदि $X _{C}>X _{L}, \phi$ धनात्मक होता है तथा परिपथ का धारितात्मक व्यवहार प्रधान हो जाता है। परिणामतः परिपथ में धारा स्रोत वोल्टता से अग्र हो जाती है। यदि $X _{C}<X _{L}, \phi$ ॠणात्मक होता है तथा परिपथ का प्रेरकीय व्यवहार प्रमुख हो जाता है। परिणामतः परिपथ में धारा स्रोत वोल्टता से पश्च हो जाती है।
चित्र 7.13, $X _{C}>X _{L}$ के प्रकरण के लिए फेजर आरेख है और यह $\omega t$ के साथ $v$ एवं $i$ में होने वाले परिवर्तन को दर्शाता है।

चित्र 7.13 (a) $V$ एवं $I$ के लिए फेजर आरेख (b) श्रेणीबद्ध LCR परिपथ के लिए $\omega t$ के साथ $v$ एवं $t$ में परिवर्तन दर्शाने वाले ग्राफ (यहाँ $X_C>X_L$ )।
इस प्रकार, फेजर्स तकनीक का उपयोग करके, हमने श्रेणीबद्ध $L C R$ परिपथ में धारा का आयाम एवं कला ज्ञात कर ली है। लेकिन $a c$ परिपथों के विश्लेषण की इस विधि में कुछ कमियाँ हैं। प्रथम तो यह कि फेज़र आरेख प्रारंभिक स्थितियों के विषय में कोई सूचना नहीं देते। आप $t$ का कोई भी यादृच्छिक मान (जैसा कि इस अध्याय में सब जगह $t _{1}$ लिया गया है) ले सकते हैं और विभिन्न फेजर्स के बीच सापेक्षिक कोण दर्शाते हुए अलग-अलग फेजर्स आरेख बना सकते हैं। इस प्रकार प्राप्त हल को स्थायी अवस्था हल कहते हैं। यह कोई व्यापक हल नहीं है। इसके अतिरिक्त एक क्षणिक हल भी होता है जो $v=0$ के लिए भी लागू होता है। व्यापक हल, क्षणिक हल एवं स्थायी अवस्था हल के योग से प्राप्त होता है। पर्याप्त दीर्घकाल के पश्चात क्षणिक हल के प्रभाव निष्प्रभावी हो जाते हैं और परिपथ के आचरण का वर्णन स्थायी अवस्था द्वारा ही हल किया जाता है।
7.6.2 अनुनाद
श्रेणीबद्ध RLC परिपथ का एक रोचक अभिलक्षण अनुनाद की परिघटना है। अनुनाद ऐसे सभी निकायों की एक सामान्य परिघटना है जिनमें एक विशिष्ट आवृत्ति से दोलन की प्रवृत्ति होती है। यह आवृत्ति उस निकाय की प्राकृतिक आवृत्ति कहलाती है। यदि इस प्रकार का कोई निकाय किसी ऐसे ऊर्जा स्रोत द्वारा संचालित हो जिसकी आवृत्ति निकाय की प्राकृतिक आवृत्ति के सन्निकट हो तो निकाय बहुत अधिक आयाम के साथ दोलन करता हुआ पाया जाता है। इसका एक सुपरिचित उदाहरण झूले पर बैठा हुआ बच्चा है। झूले की, लोलक की ही तरह मूल बिन्दु के इधर-उधर दोलन की एक प्राकृतिक आवृत्ति होती है। यदि बच्चा रस्सी को नियमित समय-अंतरालों पर खींचता है और खींचने की आवृत्ति लगभग झूले के दोलनों की प्राकृतिक आवृत्ति के बराबर हो तो झूलने का आयाम अधिक होगा (देखिए कक्षा 11 का अध्याय 13)।
$v _{m}$ आयाम एवं $\omega$ आवृत्ति की वोल्टता द्वारा संचालित $R L C$ परिपथ के लिए हम पाते हैं कि धारा आयाम,
$$ i _{m}=\frac{v _{m}}{Z}=\frac{v _{m}}{\sqrt{R^{2}+\left(X _{C}-X _{L}\right)^{2}}} $$
यहाँ $X _{c}=1 / \omega C$ एवं $X _{L}=\omega L$ अतः यदि $\omega$ को परिवर्तित किया जाए तो एक विशिष्ट आवृत्ति $\omega _{0}$ पर $X _{c}=X _{L}$ एवं प्रतिबाधा $Z$ का मान न्यूनतम $\left(Z=\sqrt{R^{2}+0^{2}}=R\right)$ हो जाता है। यह आवृत्ति अनुनादी आवृत्ति कहलाती है :
$$ X _{c}=X _{L} \text { या } \frac{1}{\omega _{0} C}=\omega _{0} L $$
$$ \begin{equation*} \text { या } \omega _{0}=\frac{1}{\sqrt{L C}} \tag{7.28} \end{equation*} $$
अनुनादी आवृत्ति पर धारा का आयाम अधिकतम होता है और इसका मान है, $i_m=v_m / R$
चित्र 7.14 किसी $R L C$ श्रेणीक्रम परिपथ के लिए $\omega$ के साथ $I _{m}$ का परिवर्तन दर्शाता है। यहाँ $L=1.00 \mathrm{mH}, C=$ $1.00 \mathrm{nF}$ है तथा $R$ के दो अलग-अलग मान (i) $R=100$ $\Omega$ एवं (ii) $R=200 \Omega$ लिए गए हैं। प्रयुक्त स्रोत के लिए $V _{m}$ $=100 \mathrm{~V}$, इस प्रकरण में $\omega _{0}=\left(\frac{1}{\sqrt{L C}}\right)=1.00 \times 10^{6}$ $\mathrm{rad} / \mathrm{s} \mathrm{I}$
हम देखते हैं कि अनुनादी आवृत्ति पर धारा का आयाम अधिकतम होता है। चूँकि $i _{m}=v _{m} / R$ अनुनाद की स्थिति में, प्रकरण (i) में धारा का परिमाण प्रकरण (ii) की स्थिति में धारा के परिमाण से दोगुना है।

चित्र 7.14 दो प्रकरणों (i) $R=100 \Omega$ एवं (ii) $R=200 \Omega$ के लिए. $\omega$ के साथ $l _{m}$ का परिवर्तन। दोनों प्रकरणों में $L=1.00 \mathrm{mH}$
अनुनादी परिपथों के तरह-तरह के अनुप्रयोग होते हैं उदाहरणार्थ, रेडियो एवं टीवी सेटों के समस्वरण की क्रियाविधि। किसी रेडियो का ऐंटिना अनेक प्रसारक स्टेशनों से संकेतों का अभिग्रहण करता है। ऐंटिना द्वारा अभिग्रहित संकेत, रेडियो के समस्वरण परिपथ में स्रोत का कार्य करते हैं, इसलिए परिपथ अनेक आवृत्तियों पर संचालित किया जा सकता है। परंतु किसी विशिष्ट रेडियो स्टेशन को सुनने के लिए हम रेडियो को समस्वरित करते हैं। समस्वरण के लिए हम समस्वरण परिपथ में लगे संधारित्र की धारिता को परिवर्तित कर परिपथ की आवृत्ति को परिवर्तित कर इस स्थिति में लाते हैं कि उसकी अनुनादी आवृत्ति अभिगृहित रेडियो संकेतों की आवृत्ति के लगभग बराबर हो जाए। जब ऐसा होता है तो परिपथ में उस विशिष्ट रेडियो स्टेशन से आने वाले संकेतों की आवृत्ति के धारा आयाम का मान अधिकतम हो जाता है।
एक महत्वपूर्ण एवं ध्यान देने योग्य तथ्य यह है कि अनुनाद की परिघटना केवल उन्हीं परिपथों द्वारा प्रदर्शित की जाती है जिनमें $L$ एवं $C$ दोनों विद्यमान होते हैं। क्योंकि केवल तभी $L$ एवं $C$ के सिरों के बीच की वोल्टता (विपरीत कला में होने के कारण) एक दूसरे को निरस्त करती हैं और धारा आयाम $v _{m} / R$ होता है तथा कुल स्रोत वोल्टता $R$ के सिरों के बीच ही प्रभावी पायी जाती है। इसका अर्थ यह हुआ कि $R L$ या $R C$ परिपथ में अनुनाद नहीं।
उदाहरण 7.6 एक $200 \Omega$ प्रतिरोधक एवं एक $15.0 \mu \mathrm{F}$ संधारित्र, किसी $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ac स्रोत से श्रेणीक्रम में जुड़े हैं। (a) परिपथ में धारा की गणना कीजिए; (b) प्रतिरोधक एवं संधारित्र के सिरों के बीच (rms) वोल्टता की गणना कीजिए। क्या इन वोल्टताओं का बीजगणितीय योग स्रोत वोल्टता से अधिक है? यदि हाँ, तो इस विरोधाभास का निराकरण कीजिए।
हल
दिया है
$R=200 \Omega, C=15.0 \mu \mathrm{F}=15.0 \times 10^{-6} \mathrm{~F}$
$V=220 \mathrm{~V}, v=50 \mathrm{~Hz}$
(a) धारा की गणना करने के लिए, हमें परिपथ की प्रतिबाधा की आवश्यकता होती है। यह होता है-
$ \begin{aligned} Z & =\sqrt{R^{2}+X _{C}^{2}}=\sqrt{R^{2}+(2 \pi v C)^{-2}} \\ & =\sqrt{(200 \Omega)^{2}+\left(2 \times 3.14 \times 50 \times 15.0 \times 10^{-6} \mathrm{~F}\right)^{-2}} \end{aligned} $
$ \begin{aligned} & =\sqrt{(200 \Omega)^{2}+(212.3 \Omega)^{2}} \\ & =291.67 \Omega \end{aligned} $
इसलिए, परिपथ में धारा है,
$$ I=\frac{V}{Z}=\frac{220 \mathrm{~V}}{291.5 \Omega}=0.755 \mathrm{~A} $$
(b) चूँकि पूरे परिपथ में समान धारा प्रवाहित हो रही है, इसलिए
$$ \begin{aligned} & V _{R}=I R=(0.755 \mathrm{~A})(200 \Omega)=151 \mathrm{~V} \\ & V _{C}=I X _{C}=(0.755 \mathrm{~A})(212.3 \Omega)=160.3 \mathrm{~V} \end{aligned} $$
दोनों वोल्टताओं $V _{R}$ एवं $V _{C}$ का बीजगणितीय योग $311.3 \mathrm{~V}$ है जो स्रोत वोल्टता $220 \mathrm{~V}$ से अधिक है। इस विरोधाभास का निराकरण किस प्रकार किया जाए? जैसा कि आपने पाठ में पढ़ा है, दोनों वोल्टताएँ समान कला में नहीं होती हैं। इसलिए उनको साधारण संख्याओं की तरह नहीं जोड़ा जा सकता है। इन वोल्टताओं में $90^{\circ}$ का कला-अंतर होता है। इसलिए इनके योग का परिमाण पाइथागोरस के प्रमेय का उपयोग करके ज्ञात किया जा सकता है। अतः,
$$V _{R+C}=\sqrt{V _{R}^{2}+V _{C}^{2}}$$ $$=220 \mathrm{~V}$$
इस प्रकार, यदि दो वोल्टताओं के बीच के कला-अंतर को गणना में लाते हुए प्रतिरोधक एवं संधारित्र के सिरों के बीच कुल वोल्टता ज्ञात की जाए तो यह स्रोत वोल्टता के बराबर ही पायी जाएगी।
7.7 $\mathrm{ac}$ परिपथों में शक्ति : शक्ति गुणांक
हम देख चुके हैं कि श्रेणीबद्ध $R L C$ परिपथ में प्रयुक्त कोई वोल्टता $v=v _{m} \sin \omega t$ इस परिपथ में धारा $i=i _{m} \sin (\omega t+\phi)$ प्रवाहित करती है। यहाँ,
$$ i _{m}=\frac{v _{m}}{Z} \text { एवं } \phi=\tan ^{-1}\left(\frac{X _{C}-X _{L}}{R}\right) $$
इसलिए स्रोत द्वारा आपूर्त तात्क्षणिक शक्ति $p$ है,
$$ \begin{align*} & p=v i=\left(v _{m} \sin \omega t\right) \times\left[i _{m} \sin (\omega t+\phi)\right] \\ & =\frac{v _{m} i _{m}}{2}[\cos \phi-\cos (2 \omega t+\phi)] \tag{7.29} \end{align*} $$
एक पूर्ण चक्र में माध्य शक्ति समीकरण (7.29) के दाएँ पक्ष के दोनों पदों का माध्य लेने से प्राप्त हो सकती है। इनमें केवल दूसरा पद ही समय पर निर्भर करता है, और इसका माध्य शून्य है (कोज्या (cosine) का धनात्मक अर्द्ध इसके ॠणात्मक अर्द्ध को निरस्त कर देता है।) इसलिए,
$$ \begin{align*} & P=\frac{v _{m} i _{m}}{2} \cos \phi=\frac{v _{m}}{\sqrt{2}} \frac{i _{m}}{\sqrt{2}} \cos \phi \\ & =V I \cos \phi \tag{30a} \end{align*} $$
इसको इस प्रकार भी लिखा जा सकता है
$$ \begin{equation*} P=I^{2} Z \cos \phi \tag{30b} \end{equation*} $$
अतः क्षयित माध्य शक्ति, न केवल वोल्टता एवं धारा पर निर्भर करती है बल्कि उनके बीच के कला-कोण की कोज्या (cosine) पर भी निर्भर करती है। राशि $\cos \phi$ को शक्ति गुणांक कहा जाता है। आइए निम्नलिखित प्रकरणों पर चर्चा करें :
प्रकरण (i) प्रतिरोधकीय परिपथ : यदि परिपथ में केवल शुद्ध $R$ है तो यह परिपथ प्रतिरोधकीय परिपथ कहलाता है। इस परिपथ के लिए $\phi=0, \cos \phi=1$ इसमें अधिकतम शक्ति क्षय होती है।
प्रकरण (ii) शुद्ध प्रेरकीय अथवा धारितीय परिपथ : यदि परिपथ में केवल एक प्रेरक अथवा संधारित्र हो तो हम जानते हैं कि धारा एवं वोल्टता के बीच कला अंतर $\pi / 2$ होता है। इसलिए $\cos \phi=0$ और इसलिए यद्यपि परिपथ में धारा प्रवाहित होती है तो भी कोई शक्ति क्षय नहीं होती। इस धारा को कभी-कभी वाटहीन धारा भी कहा जाता है।
प्रकरण (iii) श्रेणीबद्ध $L C R$ परिपथ : किसी $L C R$ परिपथ में शक्ति क्षय समीकरण (7.30) के अनुसार होता है। यहाँ $\phi=\tan ^{-1}\left(X _{c}-X _{L}\right) / R$ अतः किसी $R L$ या $R C$ या $R C L$ परिपथ में $\phi$ शून्येतर हो सकता है। इन परिपथों में भी शक्ति केवल प्रतिरोधक में ही क्षयित होती है।
प्रकरण (iv) $L C R$ परिपथ में अनुनाद स्थिति में शक्ति क्षय : अनुनाद की स्थिति में $X _{c}-X _{L}=0$ एवं $\phi=0$ इसलिए $\cos \phi=1$ एवं $P=I^{2} Z=I^{2} R$ अर्थात परिपथ में अधिकतम शक्ति ( $R$ के माध्यम से) अनुनाद की स्थिति में क्षयित होती है।
उदाहरण 7.7 (a) विद्युत शक्ति के परिवहन के लिए प्रयुक्त होने वाले परिपथों में निम्न शक्ति गुणांक, संप्रेषण में अधिक ऊर्जा का क्षय होगा, निर्दिष्ट करता है। इसका कारण समझाइए।
(b) परिपथ का शक्ति गुणांक, प्रायः परिपथ में उपयुक्त मान के संधारित्र का उपयोग करके सुधारा जा सकता है। यह तथ्य समझाइए।
हल (a) हम जानते हैं कि $P=I V \cos \phi$ यहाँ $\cos \phi$ शक्ति गुणांक है। दी गई वोल्टता पर वांछित शक्ति की आपूर्ति के लिए यदि $\cos \phi$ का मान कम होगा तो हमें उसी अनुपात में धारा का मान बढ़ाना पड़ेगा। परन्तु इससे संप्रेषण में अधिक शक्ति क्षय $\left(I^{2} R\right)$ होगा।
(b) माना कि किसी परिपथ में धारा $I$ वोल्टता से $\phi$ कोण पीछे रहती है तो इस परिपथ के लिए $\cos \phi=R / Z$
हम शक्ति गुणांक का सुधार कर इसका मान 1 की ओर प्रवृत्त कर सकते हैं जिसके लिए $Z$ का मान $R$ हो यह प्रयास करना पड़ेगा। यह उपलब्धि कैसे होती है, आइए चित्र द्वारा इसे समझने का प्रयास करें। धारा $\mathbf{I}$ को हम दो घटकों में वियोजित करते हैं- $\mathbf{I} _{p}$ प्रयुक्त वोल्टता $\mathbf{V}$ की दिशा में एवं $\mathbf{I} _{q}$ वोल्टता की लंबवत दिशा में। $\mathbf{I} _{q}$ जैसा आप अनुभाग 7.7 में पढ़ चुके हैं, वाटहीन घटक कहलाता है क्योंकि धारा के इस घटक के संगत कोई शक्ति क्षय नहीं होता। $I _{P}$ को शक्ति घटक कहा जाता है, क्योंकि यह वोल्टता के साथ समान कला में है और इसी के साथ परिपथ में शक्ति क्षय होती है। इस विश्लेषण से यह स्पष्ट है कि यदि हम शक्ति गुणांक में सुधार लाना चाहें तो पश्चगामी वाटहीन धारा $\mathbf{I} _{\mathrm{q}}$ को उसी के बराबर अग्रगामी वाटहीन धारा $\mathbf{I} _{q}^{\prime}$ द्वारा उदासीन करना पड़ेगा। इसके लिए उपयुक्त मान का संधारित्र समांतर क्रम में संयोजित करना होगा ताकि $I _{q}$ एवं $\mathbf{I} _{q}^{\prime}$ एक-दूसरे को निरस्त कर सकें और $P$ प्रभावी रूप से $I _{\mathrm{p}} V$ हो सके।

चित्र 7.15
उदाहरण 7.8 $283 \mathrm{~V}$ शिखर वोल्टता एवं $50 \mathrm{~Hz}$ आवृत्ति की एक ज्यावक्रीय वोल्टता एक श्रेणीबद्ध $L C R$ परिपथ से जुड़ी है जिसमें $R=3 \Omega, L=25.48 \mathrm{mH}$, एवं $C=796 \mu \mathrm{F}$ है। ज्ञात कीजिए (a) परिपथ की प्रतिबाधा; (b) स्रोत के सिरों के बीच लगी वोल्टता एवं परिपथ में प्रवाहित होने वाली धारा के बीच कला-अंतर; (c) परिपथ में होने वाला शक्ति-क्षय; एवं (d) शक्ति गुणांक।
हल (a) परिपथ की प्रतिबाधा ज्ञात करने के लिए पहले हम $X_{\mathrm{L}}$ एवं $X_{\mathrm{C}}$ की गणना करेंगे।
$$ \begin{aligned} & X_L=2 \pi \nu L \\ &=2 \times 3.14 \times 50 \times 25.48 \times 10^{-3} \Omega=8 \Omega \\ & X_C=\frac{1}{2 \pi v C} \\ &=\frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}}=4 \Omega \end{aligned} $$
इसलिए,
$$ \begin{aligned} Z & =\sqrt{R^2+\left(X_L-X_C\right)^2}=\sqrt{3^2+(8-4)^2} \\ & =5 \Omega \end{aligned} $$
(b) कला-अंतर, $\phi=\tan ^{-1} \frac{X_C-X_L}{R}$
$$ =\tan ^{-1}\left(\frac{4-8}{3}\right)=-53.1^{\circ} $$
चूँकि $\phi$ का मान ॠणात्मक है, परिपथ में धारा स्रोत के सिरों के बीच वोल्टता से पीछे रहती है,
(c) परिपथ में शक्ति क्षय,
$$ P=I^2 R $$
अब, $I=\frac{i_m}{\sqrt{2}}=\frac{1}{\sqrt{2}}\left(\frac{283}{5}\right)=40 \mathrm{~A}$
$ \text { अतः, } P=(40 \mathrm{~A})^2 \times 3 \Omega=4800 \mathrm{~W} $
(d) शक्ति गुणांक $=\cos \phi=\cos \left(-53.1^{\circ}\right)=0.6$
उदाहरण 7.9 माना कि पूर्व उदाहरण में वर्णित स्रोत की आवृत्ति परिवर्तनशील है। (a) स्रोत की किस आवृत्ति पर अनुनाद होगा। (b) अनुनाद की अवस्था में प्रतिबाधा, धारा एवं क्षयित शक्ति की गणना कीजिए।
हल
(a) वह आवृत्ति जिस पर अनुनाद होगा,
$$ \begin{aligned} \omega _{0} & =\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{25.48 \times 10^{-3} \times 796 \times 10^{-6}}} \\ & =222.1 \mathrm{rad} / \mathrm{s} \end{aligned} $$
$$ \begin{aligned} v _{r} & =\frac{\omega _{0}}{2 \pi}=\frac{221.1}{2 \times 3.14} \mathrm{~Hz}=35.4 \mathrm{~Hz} \end{aligned} $$
(b) अनुनाद की स्थिति में प्रतिबाधा, $Z$ प्रतिरोध, $R$ के बराबर होती है अत:
$$ Z=R=3 \Omega $$
अनुनाद स्थिति में $\mathrm{rms}$ धारा
$$ =\frac{V}{Z}=\frac{V}{R}=\left(\frac{283}{\sqrt{2}}\right) \frac{1}{3}=66.7 \mathrm{~A} $$
अनुनाद स्थिति में शक्ति क्षय
$$ P=I^{2} \times R=(66.7)^{2} \times 3=13.35 \mathrm{~kW} $$
प्रस्तुत प्रकरण में आप देख सकते हैं कि अनुनाद स्थिति में शक्ति क्षय उदाहरण 7.8 में हुए शक्ति क्षय से अधिक है।
उदाहरण 7.10 किसी हवाई अड्डे पर सुरक्षा कारणों से, किसी व्यक्ति को धातु-संसूचक के द्वार पथ से गुजारा जाता है। यदि उसके पास कोई धातु से बनी वस्तु है, तो धातु संसूचक से एक ध्वनि निकलने लगती है। यह संसूचक किस सिद्धांत पर कार्य करता है?
हल धातु संसूचक $\mathrm{ac}$ परिपथों में अनुनाद के सिद्धांत पर कार्य करता है। जब आप किसी धातु संसूचक से गुजरते है तो वास्तव में आप अनेक फेरों वाली एक कुंडली से होकर गुजरते हैं। यह कुंडली एक ऐसी समस्वरित संधारित्र से जुड़ी होती है जिसके कारण परिपथ अनुनाद की स्थिति में होता है। जब आप जेब में धातु लेकर कुंडली से गुजरते हैं तो परिपथ की प्रतिबाधा परिवर्तित हो जाती है, परिणामस्वरूप परिपथ में प्रवाहित होने वाली धारा में सार्थक परिवर्तन होता है। धारा का यह परिवर्तन संसूचित होता है एवं इलेक्ट्रॉनिक परिपथिकी के कारण चेतावनी की ध्वनि उत्पन्न होती है।
7.8 ट्रांसफॉर्मर
अनेक उद्देश्यों के लिए $a c$ वोल्टता को एक मान से दूसरे अधिक या कम मान में परिवर्तित करना (या रूपांतरित करना) आवश्यक हो जाता है। ऐसा अन्योन्य प्रेरण के सिद्धांत पर आधारित एक युक्ति के द्वारा किया जाता है जिसे ट्रांसफॉर्मर कहते हैं।
ट्रांसफार्मर में दो कुंडलियाँ होती हैं जो एक दूसरे से विद्युतरुद्ध होती हैं। वे एक कोमल-लौह-क्रोड पर लिपटी होती हैं। लपेटने की विधि या तो चित्र 7.16 (a) की भाँति होती है, जिसमें एक कुंडली दूसरी के ऊपर लिपटी होती है, या फिर चित्र 7.16 (b) की भाँति जिसमें दोनों कुंडलियाँ क्रोड की अलग-अलग भुजाओं पर लिपटी होती हैं। एक कुंडली को प्राथमिक कुंडली (primary coil) कहते हैं इसमें $N _{p}$ लपेटे होते हैं। दूसरी कुंडली को द्वितीयक कुंडली (secondary coil) कहते हैं, इसमें $N _{s}$ लपेटे होते हैं। प्राय: प्राथमिक कुंडली निवेशी कुंडली होती है एवं द्वितीयक कुंडली ट्रांसफार्मर की निर्गत कुंडली होती है।

चित्र 7.16 किसी ट्रांसफॉर्मर में प्राथमिक एवं द्वितीयक कुंडलियों को लपेटने की दो व्यवस्थाएँ: (a) एक दूसरे के ऊपर लपेटी गई दो कुंडलियाँ (b) क्रोड की अलग-अलग भुजाओं पर लिपटी कुंडलियाँ
जब प्राथमिक कुंडली के सिरों के बीच प्रत्यावर्ती वोल्टता लगाई जाती है तो परिणामी धारा एक प्रत्यावर्ती चुंबकीय फ्लक्स उत्पन्न करती है जो द्वितीयक कुंडली से संयोजित होकर इसके सिरों के बीच एक emf प्रेरित करता है। इस emf का मान द्वितीयक कुंडली में फेरों की संख्या पर निर्भर करता है। हम मान लेते हैं कि हमारा ट्रांसफॉर्मर एक आदर्श ट्रांसफॉर्मर है जिसकी प्राथमिक कुंडली का प्रतिरोध नगण्य है, और क्रोड का संपूर्ण फ्लक्स प्राथमिक एवं द्वितीयक दोनों कुंडलियों से गुजरता है। प्राथमिक कुंडली के सिरों के बीच वोल्टता $v _{p}$ लगाने से, माना किसी क्षण $t$ पर, इस कुंडली का प्रत्येक फेरा क्रोड में $\phi$ फ्लक्स उत्पन्न करता है।
तब $N _{s}$ लपेटों वाली द्वितीयक कुंडली के सिरों के बीच प्रेरित $\mathrm{emf}$ या वोल्टता $\varepsilon _{s}$ है
$$ \begin{equation*} \varepsilon _{s}=-N _{s} \frac{\mathrm{d} \phi}{\mathrm{d} t} \tag{7.31} \end{equation*} $$
प्रत्यावर्ती फ्लक्स, $\phi$ प्राथमिक कुंडली में भी एक $\mathrm{emf}$ प्रेरित करता है जिसे पश्च विद्युत वाहक बल कहते हैं। यह है,
$$ \begin{equation*} \varepsilon _{p}=-N _{p} \frac{\mathrm{d} \phi}{\mathrm{d} t} \tag{7.32} \end{equation*} $$
लेकिन, $\varepsilon _{p}=v _{p}$ यदि ऐसा नहीं होता तो प्रारंभिक कुंडली (जिसका प्रतिरोध हमने शून्य माना है) में अनंत परिमाण की धारा प्रवाहित होती। यदि द्वितीयक कुंडली के सिरे मुक्त हों अथवा इससे बहुत कम धारा ली जा रही हो तो पर्याप्त सन्निकट मान तक
$$ \varepsilon _{s}=v _{s} $$
यहाँ $v _{s}$ द्वितीयक कुंडली के सिरों के बीच वोल्टता है। अतः समीकरणों (7.31) एवं (7.32) को हम इस प्रकार लिख सकते हैं -
$$ \begin{align*} & v _{s}=-N _{s} \frac{d \phi}{d t} \tag{31a} \\ & v _{p}=-N _{p} \frac{d \phi}{d t} \tag{32a} \end{align*} $$
समीकरण [7.31 (a)] एवं [7.32 (a)] से,
$$ \begin{equation*} \frac{v _{s}}{v _{p}}=\frac{N _{s}}{N _{p}} \tag{7.33} \end{equation*} $$
ध्यान दीजिए कि उपरोक्त संबंध की व्युत्पत्ति में हमने तीन परिकल्पनाओं का उपयोग किया है जो इस प्रकार हैं- (i) प्राथमिक कुंडली का प्रतिरोध एवं इसमें प्रवाहित होने वाली धारा कम है; (ii) प्राथमिक एवं द्वितीयक कुंडली से समान फ्लक्स बाहर निकल पाता है; एवं (iii) द्वितीयक कुंडली में बहुत कम धारा प्रवाहित होती है।
यदि यह मान लिया जाए कि ट्रांसफॉर्मर की दक्षता $100 %$ है (कोई ऊर्जा क्षय नहीं होता); तो निवेशी शक्ति, निर्गत शक्ति के बराबर होगी और चूँकि $p=i v$,
$$ \begin{equation*} i _{p} v _{p}=i _{s} v _{s} \tag{7.34} \end{equation*} $$
यद्यपि कुछ न कुछ ऊर्जा क्षय तो सदैव होता ही है, फिर भी यह एक अच्छा सन्निकटन है, क्योंकि एक भली प्रकार अभिकल्पित ट्रांसफॉर्मर की दक्षता $95 %$ से अधिक होती है। समीकरण (7.33) एवं (7.34) को संयोजित करने पर,
$$ \begin{equation*} \frac{i _{p}}{i _{s}}=\frac{v _{s}}{v _{p}}=\frac{N _{s}}{N _{p}} \tag{7.35} \end{equation*} $$
क्योंकि $i$ एवं $v$ दोनों की दोलन आवृत्ति वही है जो $\mathrm{ac}$ स्रोत की, समीकरण (7.35) से संगत राशियों के आयामों अथवा $\mathrm{rms}$ मानों का अनुपात भी प्राप्त होता है।
अब, हम देख सकते हैं कि ट्रांसफॉर्मर किस प्रकार वोल्टता एवं धारा के मानों को प्रभावित करता है। हम जानते हैं कि :
$$ \begin{equation*} V _{s}=\left(\frac{N _{s}}{N _{p}}\right) V _{p} \quad \text { तथा } I _{s}=\left(\frac{N _{p}}{N _{s}}\right) I _{p} \tag{7.36} \end{equation*} $$
अर्थात यदि द्वितीयक कुंडली में प्राथमिक कुंडली से अधिक फेरे हैं $\left(N _{s}>N _{p}\right)$ तो वोल्टता बढ़ जाती है $\left(V _{s}>V _{p}\right)$ । इस प्रकार की व्यवस्था को उच्चायी ट्रांसफॉर्मर (step-up transformer) कहते हैं। तथापि, इस व्यवस्था में, द्वितीयक कुंडली में धारा प्राथमिक कुंडली से कम होती है $\left(N _{p} / N _{s}<1\right.$ एवं $\left.I _{s}<I _{p}\right)$ । उदाहरणार्थ, यदि किसी ट्रांसफॉर्मर की प्राथमिक कुंडली में 100 एवं द्वितीयक कुंडली में 200 फेरे हों तो $N _{s} / N _{p}=2$ एवं $N _{p} / N _{s}=1 / 2$ । अत: $220 \mathrm{~V}$, $10 \mathrm{~A}$ का निवेश, बढ़कर $440 \mathrm{~V}$ का निर्गम $5.0 \mathrm{~A}$ पर देगा।
यदि द्वितीयक कुंडली में प्राथमिक कुंडली से कम फेरे हैं $\left(N _{s}<N _{p}\right)$ तो यह ट्रांसफॉर्मर अपचयी (step-down transformer) है। इस ट्रांसफार्मर में $V _{s}<V _{p}$ एवं $I _{s}>I _{p}$ अर्थात वोल्टता कम हो जाती है तथा धारा बढ़ जाती है।
ऊपर प्राप्त की गई समीकरण आदर्श ट्रांसफॉर्मरों के लिए ही लागू होती है (जिनमें कोई ऊर्जा क्षय नहीं होता)। परंतु वास्तविक ट्रॉसफॉर्मरों में निम्नलिखित कारणों से अल्प मात्रा में ऊर्जा क्षय होता है-
(i) फ्लक्स क्षरण-सदैव कुछ न कुछ फ्लक्स तो क्षरित होता ही है, अर्थात क्रोड के खराब अभिकल्पन या इसमें रही वायु रिक्ति के कारण, प्राथमिक कुंडली का समस्त फ्लक्स द्वितीयक कुंडली से नहीं गुजरता। प्राथमिक एवं द्वितीयक कुंडलियों को एक दूसरे के ऊपर लपेट कर फ्लक्स क्षरण को कम किया जाता है।
(ii) कुंडलनों का प्रतिरोध- कुंडलियाँ बनाने में लगे तारों का कुछ न कुछ प्रतिरोध तो होता ही है और इसलिए इन तारों में उत्पन्न ऊष्मा $\left(I^{2} R\right)$ के कारण ऊर्जा क्षय होता है। उच्च धारा, निम्न वोल्टता कुंडलनों में मोटे तार का उपयोग करके, इनमें होने वाले ऊर्जा क्षय को कम किया जाता है।
(iii) भँवर धाराएँ-प्रत्यावर्ती चुंबकीय फ्लक्स, लौह-क्रोड में भँवर धाराएँ प्रेरित करके, इसे गर्म कर देता है। स्तरित क्रोड का उपयोग करके इस प्रभाव को कम किया जाता है।
(iv) शैथिल्य (Hysteresis)-प्रत्यावर्ती चुंबकीय क्षेत्र द्वारा क्रोड का चुंबकन बार-बार उत्क्रमित होता है। इस प्रक्रिया में व्यय होने वाली ऊर्जा क्रोड में ऊष्मा के रूप में प्रकट होती है। कम शैथिल्य वाले पदार्थ का क्रोड में उपयोग करके इस प्रभाव को कम रखा जाता है।
विद्युत ऊर्जा का लंबी दूरियों तक, बड़े पैमाने पर संप्रेषण एवं वितरण करने के लिए ट्रांसफॉर्मरों का उपयोग किया जाता है। जनित्र की निर्गत वोल्टता को उच्चायित किया जाता है (ताकि धारा कम हो जाती है और परिणामस्वरूप $I^{2} R$ हानि घट जाती है। इसकी लंबी दूरी के उपभोक्ता के समीप स्थित क्षेत्रीय उप-स्टेशन तक संप्रेषित किया जाता है। वहाँ वोल्टता को अपचयित किया जाता है। वितरण उप-स्टेशनों एवं खंभों पर फिर से अपचयित करके $240 \mathrm{~V}$ की शक्ति आपूर्ति हमारे घरों को पहुँचायी जाती है।
सारांश
1. जब किसी प्रतिरोधक $R$ के सिरों पर कोई प्रत्यावर्ती वोल्टता $v=v _{m} \sin \omega t$ लगाई जाती है तो उसमें धारा $i=i _{m} \sin \omega t$ संचालित होती है जहाँ, $i _{m}=\frac{v _{m}}{R}$. यह धारा प्रयुक्त वोल्टता की कला में होती है।
2. किसी प्रतिरोधक $R$ से प्रवाहित प्रत्यावर्ती धारा $i=i _{m} \sin \omega t$ के लिए जूल तापन के कारण माध्य शक्ति क्षय $(1 / 2) i _{m}^{2} R$ होता है। इसे उसी रूप में व्यक्त करने के लिए जिसमें $\mathrm{dc}$ शक्ति $\left(P=I^{2} R\right)$, को व्यक्त करते हैं, धारा के एक विशिष्ट मान का उपयोग किया जाता है। इसे वर्ग माध्य मूल (rms) धारा कहते हैं तथा $I$ से व्यक्त करते हैं :
$$ I=\frac{i _{m}}{\sqrt{2}}=0.707 i _{m} $$
इसी प्रकार, $r m s$ वोल्टता
$$ V=\frac{v _{m}}{\sqrt{2}}=0.707 v _{m} $$
माध्य शक्ति के लिए व्यंजक $P=I V=I^{2} R$
3. किसी शुद्ध प्रेरक $L$ के किसी पर प्रयुक्त ac वोल्टता $v=v _{m} \sin \omega t$ इसमें $i=i _{m} \sin$ $(\omega t-\pi / 2)$, धारा संचालित करता है, यहाँ $i _{m}=\frac{v _{m}}{X _{L}} \quad$ जहाँ $\quad X _{L}=\omega L$ $X _{L}$ को प्रेरणिक प्रतिघात कहते हैं। प्रेरक में धारा वोल्टता से $\pi / 2$ रेडियन से पीछे होती है। एक पूरे चक्र में किसी प्रेरिक को आपूर्ति माध्य शक्ति शून्य होती है।
4. किसी संधारित्र के सिरों पर प्रयुक्त ac वोल्टता $v=v _{m} \sin \omega t$ उसमें $i=i _{m} \sin (\omega t+\pi)$ 2) धारा संचालित करता है। यहाँ
$i _{m}=\frac{v _{m}}{X _{C}}, X _{C}=\frac{1}{\omega C}$
$X _{C}$ को धारिता प्रतिघात कहते हैं। संधारित्र में प्रवाहित धारा प्रयुक्त वोल्टता से $\pi / 2$ रेडियन आगे होती है। प्रेरक के समान ही एक पूरे चक्र में संधारित्र को आपूर्त माध्य शक्ति शून्य होती है।
5. वोल्टता $v=v _{m} \sin \omega t$, द्वारा संचालित किसी श्रेणीबद्ध $L C R$ परिपथ में धारा का मान निम्नलिखित व्यंजक से दिया जाता है,
यहाँ $i _{m}=\frac{v _{m}}{\sqrt{R^{2}+\left(X _{C}-X _{L}\right)^{2}}}$
तथा $\phi=\tan ^{-1} \frac{X _{C}-X _{L}}{R}$ होता है।
$Z=\sqrt{R^{2}+\left(X _{C}-X _{L}\right)^{2}}$ को परिपथ की प्रतिबाधा कहते हैं।
एक पूरे चक्र में माध्य शक्ति क्षय को निम्न सूत्र से व्यक्त करते हैं,
$$ P=V I \cos \phi $$
पद $\cos \phi$ को शक्ति गुणांक कहते हैं।
6. किसी विशुद्ध प्रेरणिक अथवा धारिता परिपथ के लिए $\cos \phi=0$ । ऐसे परिपथ में यद्यपि धारा तो प्रवाहित होती है तथापि शक्ति क्षय नहीं होता है। ऐसे उदाहरणों में धारा को वाटहीन (Wattless) धारा कहते हैं।
7. किसी ac परिपथ में धारा व वोल्टता के मध्य कला के संबंध को सुगमता से व्यक्त किया जा सकता है। इसमें वोल्टता तथा धारा को घूर्णी सदिशों से निरूपित करते हैं। घूर्णी सदिश को फेजर कहते हैं। फेजर एक सदिश के समान है जो $\omega$ चाल से मूल बिंदु के चतुर्दिश घूर्णन करता है। फेजर का परिमाण फेजर द्वारा निरूपित राशि (वोल्टता या धारा) के आयाम या शिखर मान को व्यक्त करता है।
फेजर-आरेख के उपयोग से किसी $\mathrm{ac}$ परिपथ का विश्लेषण आसान हो जाता है।
8. ट्रांसफार्मर में एक लोहे का क्रोड होता है जिसमें फेरों की संख्या $N _{p}$ की एक प्राथमिक कुंडली तथा फेरों की संख्या $N _{s}$ की एक द्वितीयक कुंडली लिपटी रहती है। यदि प्राथमिक कुंडली को किसी $\mathrm{ac}$ स्रोत से जोड़ दें, तो प्राथमिक एवं द्वितीयक वोल्टता निम्नलिखित व्यंजक द्वारा संबंधित होती हैं,
$$ V _{s}=\left(\frac{N _{s}}{N _{p}}\right) V _{p} $$
तथा दोनों धाराओं के मध्य के संबंध को निम्नलिखित सूत्र से व्यक्त करते हैं
$$ I _{s}=\left(\frac{N _{p}}{N _{s}}\right) I _{p} $$
यदि प्राथमिक की तुलना में द्वितीयक कुंडली में फेरों की संख्या अधिक है तो वोल्टता उच्च हो जाती है $\left(V _{s}>V _{R}\right)$ । इस प्रकार की युक्ति को उच्चायी ट्रांसफार्मर कहते हैं। किंतु यदि प्राथमिक की तुलना में द्वितीयक में फेरों की संख्या कम है तो ट्रांसफार्मर अपचयी होता है।
| भौतिक राशि | प्रतीक | विमा | मात्रक | टिप्पणी |
|---|---|---|---|---|
| rms वोल्टता | $V _{r m s}$ | $\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right]$ | V | $V _{r m s}=\frac{V _{m}}{\sqrt{2}}, V _{\mathrm{m}}$ ac वोल्टता का आयाम है। |
| rms धारा | $I _{r m s}$ | [A] | A | $I _{r m s}=\frac{I _{m}}{\sqrt{2}}, I _{\mathrm{m}}$ ac धारा का आयाम है। |
| प्रतिघात : प्रेरणिक धारितात्मक |
$X _{\mathrm{L}}$ $X _{\mathrm{C}}$ |
$\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-3} \mathrm{~A}^{-2}\right]$ $\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-3} \mathrm{~A}^{-2}\right]$ |
$\Omega$ $\Omega$ |
$X _{\mathrm{L}}=\omega L$ $X _{\mathrm{C}}=1 / \omega C$ |
| प्रतिबाधा | $Z$ | $\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-3} \mathrm{~A}^{-2}\right]$ | $\Omega$ | परिपथ में विद्यमान अवयवों पर निर्भर करता है। |
| अनुनादी आवृत्ति |
$\omega _{\mathrm{r}}$ या $\omega _{0}$ | $\left[\mathrm{~T}^{-1}\right]$ | $\omega _{\mathrm{r}}=\frac{1}{\sqrt{L C}}$ एक श्रेणीबद्ध $L C R$ परिपथ के लिए |
|
| गुणता कारक | $Q$ | विमाह | $Q=\frac{\omega _{r} L}{R}=\frac{1}{\omega _{r} C R}$ श्रेणीबद्ध $L C R$ परिपथ के लिए |
|
| शक्ति कारक | विमाहीन | $=\cos \phi, \phi$ परिपथ में आरोपित वोल्टता तथा धारा में कलांतर है |
विचारणीय विषय
1. जब ac वोल्टता या धारा को कोई मान दिया जाता है तो यह प्राय: धारा अथवा वोल्टता का rms मान होता है। आपके कमरे में लगे विद्युत स्विच के टर्मिनलों के बीच वोल्टता सामान्यतया $240 \mathrm{~V}$ होती है। यह वोल्टता के rms मान को निर्दिष्ट करती है। इस वोल्टता का आयाम है।
$$ V _{m}=\sqrt{2} V _{r m s}=\sqrt{2}(240)=340 \mathrm{~V} $$
2. किसी $\mathrm{ac}$ परिपथ में प्रयुक्त अवयव की शक्ति संनिर्धारण माध्य शक्ति से निर्धारण को इंगित करती है।
3. किसी $\mathrm{ac}$ परिपथ में उपयुक्त शक्ति कभी भी ऋणात्मक नहीं होती।
4. प्रत्यावर्ती एवं दिष्ट धाराएँ दोनों ऐम्पियर में मापी जाती हैं। किंतु प्रत्यावर्ती धारा के लिए ऐम्पियर को किस प्रकार भौतिक रूप से परिभाषित किया जाए? जिस प्रकार $\mathrm{dc}$ ऐम्पियर को परिभाषित करते हैं उसी प्रकार इसे ( $\mathrm{ac}$ ऐम्पियर को) $\mathrm{ac}$ धाराओं को वहन करने वाले दो समांतर तारों के अन्योन्य आकर्षण के रूप में परिभाषित नहीं कर सकते। $\mathrm{ac}$ धारा स्रोत की आवृत्ति के साथ दिशा परिवर्तित करती है जिससे माध्य आकर्षण बल शून्य हो जाता है। अतः ac ऐम्पियर को किसी ऐसे गुण के संबंध में परिभाषित करना चाहिए जो धारा की दिशा पर निर्भर न करता हो। जूल तापन एक ऐसा ही गुण है, तथा किसी परिपथ में प्रत्यावर्ती धारा के $r m s$ मान को एक ऐम्पियर के रूप में परिभाषित करते हैं यदि यह धारा वही औसत ऊष्मीय प्रभाव उत्पन्न करती है, जैसा कि $\mathrm{dc}$ धारा की एक ऐम्पियर उन्हीं परिस्थितियों में करती है।
5. किसी $\mathrm{ac}$ परिपथ में विभिन्न अवयवों के सिरों के बीच वोल्टताओं का योग करते समय उनकी कलाओं का उचित ध्यान रखना चाहिए। उदाहरणार्थ, यदि किसी $R C$ परिपथ में $V _{R}$ और $V _{C}$ क्रमशः $R$ व $C$ के सिरों के बीच वोल्टता है तो $R C$ संयोजन के सिरों के बीच वोल्टता $V _{R C}=\sqrt{V _{R}^{2}+V _{C}^{2}}$ होगी न कि $V _{R}+V _{C}$ क्योंकि $V _{C}$ तथा $V _{R}$ के बीच कला-अंतर $\frac{\pi}{2}$ है।
6. यद्यपि किसी फेजर-आरेख में वोल्टता तथा धारा को सदिशों से निरूपित करते हैं तथापि ये राशियाँ वास्तव में सदिश नहीं हैं। ये अदिश राशियाँ हैं। ऐसा होता है कि सरल आवर्त रूप से परिवर्तित होने वाले अदिशों की कलाएँ गणितीय रूप से उसी प्रकार संयोग करती हैं, जैसे कि तदनुसार परिमाणों व दिशाओं के घूर्णी सदिशों के प्रक्षेप करते हैं। ‘घूर्णी सदिश’, जो सरल आवर्त रूप से परिवर्तनशील अदिश राशियों का निरूपण करते हैं, हमें इन राशियों के जोड़ने की सरल विधि प्रदान करने के लिए सन्निविष्ट किए जाते हैं। इसके लिए हम उस नियम का उपयोग करते हैं जिसे हम सदिशों के संयोजन के नियम के रूप में पहले ही से जानते हैं।
7. किसी $\mathrm{ac}$ परिपथ में शुद्ध संधारित्रों तथा प्रेरकों से कोई शक्ति-क्षय संबद्ध नहीं होता। यदि $\mathrm{ac}$ परिपथ में किसी अवयव द्वारा शक्ति-क्षय होता है तो वह प्रतिरोधक अवयव है।
8. किसी $L C R$ परिपथ में अनुनाद की परिघटना तब होती है जब $X _{L}=X _{C}$ या $\omega _{0}=\frac{1}{\sqrt{L C}}$ । अनुनाद होने के लिए परिपथ में $L$ व $C$ दोनों अवयवों का होना आवश्यक है। इनमें से मात्र एक ( $L$ अथवा $C$ ) के होने से वोल्टता के निरस्त होने की संभावना नहीं होती और इस प्रकार अनुनाद संभव नहीं है।
9. किसी $L C R$ परिपथ में शक्ति गुणांक (Power Factor) इस बात को मापता है कि परिपथ अधिकतम शक्ति व्यय करने के कितने समीप है।
10. जनित्रों एवं मोटरों में निवेश तथा निर्गत की भूमिकाएँ एक-दूसरे के विपरीत होती हैं। एक मोटर में वैद्युत ऊर्जा निवेश है तथा यांत्रिक ऊर्जा निर्गत है; जनित्र में यांत्रिक ऊर्जा निवेश है तथा वैद्युत ऊर्जा निर्गत है। दोनों युक्तियाँ ऊर्जा को एक प्रकार से दूसरे में रूपांतरित करती हैं।
11. एक ट्रांसफॉर्मर (उच्चायी) निम्न वोल्टता को उच्च वोल्टता में परिवर्तित करता है। यह ऊर्जा के संरक्षण के नियम का उल्लंघन नहीं करता है। धारा उसी अनुपात में घट जाती है।
अभ्यास
7.1 एक $100 \Omega$ का प्रतिरोधक $200 \mathrm{~V}, 50 \mathrm{~Hz}$ आपूर्ति से संयोजित है।
(a) परिपथ में धारा का rms मान कितना है?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है।
Show Answer
# Content Missing7.2 (a) ac आपूर्ति का शिखर मान $300 \mathrm{~V}$ है। rms वोल्टता कितनी है?
(b) ac परिपथ में धारा का $r m s$ मान $10 \mathrm{~A}$ है। शिखर धारा कितनी है?
Show Answer
# Content Missing7.3 एक $44 \mathrm{mH}$ का प्रेरित्र $220 \mathrm{~V}, 50 \mathrm{~Hz}$ आपूर्ति से जोड़ा गया है। परिपथ में धारा के rms मान को ज्ञात कीजिए।
Show Answer
# Content Missing7.4 एक $60 \mu \mathrm{F}$ का संधारित्र $110 \mathrm{~V}, 60 \mathrm{~Hz}$ ac आपूर्ति से जोड़ा गया है। परिपथ में धारा के $\mathrm{rms}$ मान को ज्ञात कीजिए।
Show Answer
# Content Missing7.5 अभ्यास 7.3 व 7.4 में एक पूरे चक्र की अवधि में प्रत्येक परिपथ में कितनी नेट शक्ति अवशोषित होती है? अपने उत्तर का विवरण दीजिए।
Show Answer
# Content Missing7.6 $30 \mu \mathrm{F}$ का एक आवेशित संधारित्र $27 \mathrm{mH}$ के प्रेरित्र से जोड़ा गया है। परिपथ के मुक्त दोलनों की कोणीय आवृत्ति कितनी है?
Show Answer
# Content Missing7.7 एक श्रेणीबद्ध $L C R$ परिपथ को, जिसमें $R=20 \Omega, L=1.5 \mathrm{H}$ तथा $C=35 \mu \mathrm{F}$, एक परिवर्ती आवृत्ति की $200 \mathrm{~V} \mathrm{ac}$ आपूर्ति से जोड़ा गया है। जब आपूर्ति की आवृत्ति परिपथ की मूल आवृत्ति के बराबर होती है तो एक पूरे चक्र में परिपथ को स्थानांतरित की गई माध्य शक्ति कितनी होगी?
Show Answer
# Content Missing7.8 चित्र 7.17 में एक श्रेणीबद्ध $L C R$ परिपथ दिखलाया गया है जिसे परिवर्ती आवृत्ति के 230 $\mathrm{V}$ के स्रोत से जोड़ा गया है। $L=5.0 \mathrm{H}, C=80 \mu \mathrm{F}, R=40 \Omega$

चित्र 7.17
(a) स्रोत की आवृत्ति निकालिए जो परिपथ में अनुनाद उत्पन्न करे।
(b) परिपथ की प्रतिबाधा तथा अनुनादी आवृत्ति पर धारा का आयाम निकालिए।
(c) परिपथ के तीनों अवयवों के सिरों पर विभवपात के rms मानों को निकालिए। दिखलाइए कि अनुनादी आवृत्ति पर $L C$ संयोग के सिरों पर विभवपात शून्य है।










