Chapter-05 Continuity and Differentiability
The whole of science is nothing more than a refinement of everyday thinking." - ALBERT EINSTEIN
5.1 Introduction
This chapter is essentially a continuation of our study of differentiation of functions in Class XI. We had learnt to differentiate certain functions like polynomial functions and trigonometric functions. In this chapter, we introduce the very important concepts of continuity, differentiability and relations between them. We will also learn differentiation of inverse trigonometric functions. Further, we introduce a new class of functions called exponential and logarithmic functions. These functions lead to powerful techniques of differentiation. We illustrate certain geometrically obvious conditions through differential calculus. In the process, we will learn some fundamental theorems in this area.

5.2 Continuity
We start the section with two informal examples to get a feel of continuity. Consider the function
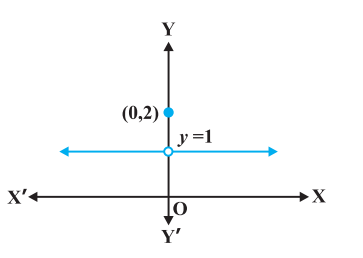
$$ f(x)=\begin{cases} 1, \text{ if } x \leq 0 \\ 2, \text{ if } x>0 \end{cases}. $$
This function is of course defined at every point of the real line. Graph of this function is given in the Fig 5.1. One can deduce from the graph that the value of the function at nearby points on $x$-axis remain close to each other except at $x=0$. At the points near and to the left of 0 , i.e., at points like $-0.1,-0.01,-0.001$, the value of the function is 1 . At the points near and to the right of 0 , i.e., at points like $0.1,0.01$,

0.001 , the value of the function is 2 . Using the language of left and right hand limits, we may say that the left (respectively right) hand limit of $f$ at 0 is 1 (respectively 2). In particular the left and right hand limits do not coincide. We also observe that the value of the function at $x=0$ concides with the left hand limit. Note that when we try to draw the graph, we cannot draw it in one stroke, i.e., without lifting pen from the plane of the paper, we can not draw the graph of this function. In fact, we need to lift the pen when we come to 0 from left. This is one instance of function being not continuous at $x=0$.
Now, consider the function defined as
$$ f(x)=\begin{cases} & 1, \text{ if } x \neq 0 \\ & 2, \text{ if } x=0 \end{cases} $$
This function is also defined at every point. Left and the right hand limits at $x=0$ are both equal to 1 . But the value of the function at $x=0$ equals 2 which does not coincide with the common value of the left and right hand limits. Again, we note that we cannot draw the graph of the function without lifting the pen. This is yet another instance of a function being not continuous at $x=0$.
Naively, we may say that a function is continuous at a fixed point if we can draw the graph of the function around that point without lifting the pen from the plane of the paper.
Mathematically, it may be phrased precisely as follows:
Definition 1 Suppose $f$ is a real function on a subset of the real numbers and let $c$ be a point in the domain of $f$. Then $f$ is continuous at $c$ if
$$ \lim _{x \to c} f(x)=f(c) $$
More elaborately, if the left hand limit, right hand limit and the value of the function at $x=c$ exist and equal to each other, then $f$ is said to be continuous at $x=c$. Recall that if the right hand and left hand limits at $x=c$ coincide, then we say that the common value is the limit of the function at $x=c$. Hence we may also rephrase the definition of continuity as follows: a function is continuous at $x=c$ if the function is defined at $x=c$ and if the value of the function at $x=c$ equals the limit of the function at $x=c$. If $f$ is not continuous at $c$, we say $f$ is discontinuous at $c$ and $c$ is called a point of discontinuity of $f$.
Example 1 Check the continuity of the function $f$ given by $f(x)=2 x+3$ at $x=1$.
Solution First note that the function is defined at the given point $x=1$ and its value is 5 . Then find the limit of the function at $x=1$. Clearly
$$ \lim _{x \to 1} f(x)=\lim _{x \to 1}(2 x+3)=2(1)+3=5 $$
Thus $\qquad \lim _{x \to 1} f(x)=5=f(1)$
Hence, $f$ is continuous at $x=1$.
Example 2 Examine whether the function $f$ given by $f(x)=x^{2}$ is continuous at $x=0$.
Solution First note that the function is defined at the given point $x=0$ and its value is 0 . Then find the limit of the function at $x=0$. Clearly
$$ \lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0} x^{2}=0^{2}=0 $$
Thus $\qquad \lim _{x \rightarrow 0} f(x)=0=f(0)$
Hence, $f$ is continuous at $x=0$.
Example 3 Discuss the continuity of the function $f$ given by $f(x)=|x|$ at $x=0$.
Solution By definition
$$ f(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases} $$
Clearly the function is defined at 0 and $f(0)=0$. Left hand limit of $f$ at 0 is
$$ \lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{-}}(-x)=0 $$
Similarly, the right hand limit of $f$ at 0 is
$$ \lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}} x=0 $$
Thus, the left hand limit, right hand limit and the value of the function coincide at $x=0$. Hence, $f$ is continuous at $x=0$.
Example 4 Show that the function $f$ given by
$$ f(x)= \begin{cases}x^{3}+3, & \text{ if } x \neq 0 \\ 1, & \text{ if } x=0\end{cases} $$
is not continuous at $x=0$.
Solution The function is defined at $x=0$ and its value at $x=0$ is 1 . When $x \neq 0$, the function is given by a polynomial. Hence,
$$ \lim _{x \to 0} f(x)=\lim _{x \to 0}(x^{3}+3)=0^{3}+3=3 $$
Since the limit of $f$ at $x=0$ does not coincide with $f(0)$, the function is not continuous at $x=0$. It may be noted that $x=0$ is the only point of discontinuity for this function.
Example 5 Check the points where the constant function $f(x)=k$ is continuous.
Solution The function is defined at all real numbers and by definition, its value at any real number equals $k$. Let $c$ be any real number. Then
$$ \lim _{x \to c} f(x)=\lim _{x \to c} k=k $$
Since $f(c)=k=\lim _{x \to c} f(x)$ for any real number $c$, the function $f$ is continuous at every real number.
Example 6 Prove that the identity function on real numbers given by $f(x)=x$ is continuous at every real number.
Solution The function is clearly defined at every point and $f(c)=c$ for every real number $c$.
Also, $\lim _{x \to c} f(x)=\lim _{x \to c} x=c$
Thus, $\lim _{x \to c} f(x)=c=f(c)$ and hence the function is continuous at every real number.
Having defined continuity of a function at a given point, now we make a natural extension of this definition to discuss continuity of a function.
Definition 2 A real function $f$ is said to be continuous if it is continuous at every point in the domain of $f$. This definition requires a bit of elaboration. Suppose $f$ is a function defined on a closed interval $[a, b]$, then for $f$ to be continuous, it needs to be continuous at every point in $[a, b]$ including the end points $a$ and $b$. Continuity of $f$ at $a$ means and continuity of $f$ at $b$ means
$$ \lim _{x \rightarrow a^{+}} f(x)=f(a) $$
$$ \lim _{x \rightarrow b^{-}} f(x)=f(b) $$
Observe that $\lim _{x \to a^{-}} f(x)$ and $\lim _{x \to b^{+}} f(x)$ do not make sense. As a consequence of this definition, iff is defined only at one point, it is continuous there, i.e., if the domain of $f$ is a singleton, $f$ is a continuous function.
Example 7 Is the function defined by $f(x)=|x|$, a continuous function?
Solution We may rewrite $f$ as
$ f(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases} $
By Example 3, we know that $f$ is continuous at $x=0$.
Let $c$ be a real number such that $c<0$. Then $f(c)=-c$.
Also $$\lim _{x \to c} f(x)=\lim _{x \to c}(-x)=-c$$
Since $\lim _{x \to c} f(x)=f(c), f$ is continuous at all negative real numbers.
Now, let $c$ be a real number such that $c>0$. Then $f(c)=c$. Also
$$ \lim _{x \to c} f(x)=\lim _{x \to c} x=c $$
Since $\lim _{x \to c} f(x)=f(c), f$ is continuous at all positive real numbers. Hence, $f$ is continuous at all points.
Example 8 Discuss the continuity of the function $f$ given by $f(x)=x^{3}+x^{2}-1$.
Solution Clearly $f$ is defined at every real number $c$ and its value at $c$ is $c^{3}+c^{2}-1$. We also know that
$$ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}\left(x^{3}+x^{2}-1\right)=c^{3}+c^{2}-1 $$
Thus $\lim _{x \to c} f(x)=f(c)$, and hence $f$ is continuous at every real number. This means $f$ is a continuous function.
Example 9 Discuss the continuity of the function $f$ defined by $f(x)=\frac{1}{x}, x \neq 0$.
Solution Fix any non zero real number $c$, we have
$$ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} \frac{1}{x}=\frac{1}{c} $$
Also, since for $c \neq 0, f(c)=\frac{1}{c}$, we have $\lim _{x \to c} f(x)=f(c)$ and hence, $f$ is continuous at every point in the domain of $f$. Thus $f$ is a continuous function.
We take this opportunity to explain the concept of infinity. This we do by analysing the function $f(x)=\frac{1}{x}$ near $x=0$. To carry out this analysis we follow the usual trick of finding the value of the function at real numbers close to 0 . Essentially we are trying to find the right hand limit of $f$ at 0 . We tabulate this in the following (Table 5.1).
Table 5.1
| x | 1 | 0.3 | 0.2 | $0.=10^{-1}$ | $ 0.01=10^{-2} $ | $ 0.001=10^{-3} $ | $ 10^n $ |
|---|---|---|---|---|---|---|---|
| f(x) | 1 | 3.333… | 5 | 10 | $ 100=10^2 $ | $1000=10^3$ | $ 10^n $ |
We observe that as $x$ gets closer to 0 from the right, the value of $f(x)$ shoots up higher. This may be rephrased as: the value of $f(x)$ may be made larger than any given number by choosing a positive real number very close to 0 . In symbols, we write
$$ \lim _{x \rightarrow 0^{+}} f(x)=+\infty $$
(to be read as: the right hand limit of $f(x)$ at 0 is plus infinity). We wish to emphasise that $+\infty$ is NOT a real number and hence the right hand limit of $f$ at 0 does not exist (as a real number).
Similarly, the left hand limit of $f$ at 0 may be found. The following table is self explanatory.
Table 5.2
| x | -1 | -0.3 | -0.2 | $-10^{-1}$ | $ -10^{-2} $ | $ -=10^{-3} $ | $ -10^n $ |
|---|---|---|---|---|---|---|---|
| f(x) | -1 | -3.333… | -5 | -10 | $-10^2 $ | $-10^3$ | $ -10^n $ |
From the Table 5.2, we deduce that the value of $f(x)$ may be made smaller than any given number by choosing a negative real number very close to 0 . In symbols, we write
$$ \lim _{x \to 0^{-}} f(x)=-\infty $$
(to be read as: the left hand limit of $f(x)$ at 0 is minus infinity). Again, we wish to emphasise that $-\infty$ is NOT a real number and hence the left hand limit of $f$ at 0 does not exist (as a real number). The graph of the reciprocal function given in Fig 5.3 is a geometric representation of the above mentioned facts.
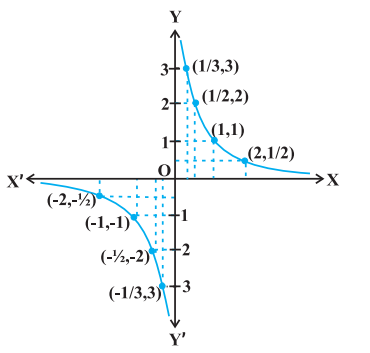
Fig 5.3
Example 10 Discuss the continuity of the function $f$ defined by
$$ f(x)=\begin{cases} x+2, \text{ if } x \leq 1 \\ x-2, \text{ if } x1 > 1 \\ \end{cases}. $$
Solution The function $f$ is defined at all points of the real line.
Case 1 If $c<1$, then $f(c)=c+2$. Therefore, $\lim _{x \to c} f(x)=\lim _{x \to c}(x+2)=c+2$
Thus, $f$ is continuous at all real numbers less than 1 .
Case 2 If $c>1$, then $f(c)=c-2$. Therefore,
$ \lim _{x \to c} f(x)=\lim _{x \to c}(x-2)=c-2=f(c) $
Thus, $f$ is continuous at all points $x>1$.
Case 3 If $c=1$, then the left hand limit of $f$ at $x=1$ is
$$ \lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(x+2)=1+2=3 $$
The right hand limit of $f$ at $x=1$ is
$$ \lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(x-2)=1-2=-1 $$
Since the left and right hand limits of $f$ at $x=1$ do not coincide, $f$ is not continuous at $x=1$. Hence
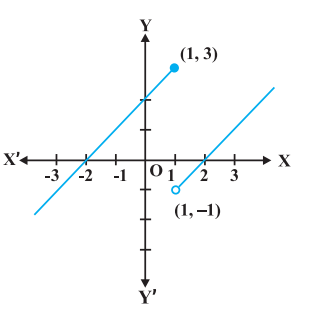
Fig 5.4
$x=1$ is the only point of discontinuity of $f$. The graph of the function is given in Fig 5.4.
Example 11 Find all the points of discontinuity of the function $f$ defined by
$$ f(x)=\begin{cases} x+2, \text{ if } x<1 \\ 0, \text{ if } \quad x=1 \\ x-2, \text{ if } x>1 \end{cases}. $$
Solution As in the previous example we find that $f$ is continuous at all real numbers $x \neq 1$. The left hand limit of $f$ at $x=1$ is
$ \lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(x+2)=1+2=3 $
The right hand limit of $f$ at $x=1$ is
$ \lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(x-2)=1-2=-1 $
Since, the left and right hand limits of $f$ at $x=1$ do not coincide, $f$ is not continuous at $x=1$. Hence $x=1$ is the only point of discontinuity of $f$. The graph of the function is given in the Fig 5.5.
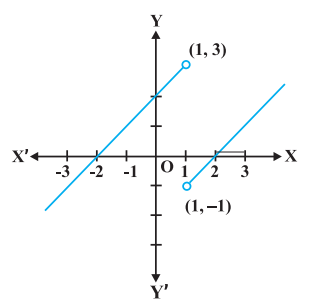
Fig 5.5
Example 12 Discuss the continuity of the function defined by
$$ f(x)=\begin{cases} x+2, \text{ if } x<0 \\ -x+2, \text{ if } x>0 \end{cases}. $$
Solution Observe that the function is defined at all real numbers except at 0 . Domain of definition of this function is
$ \begin{aligned} D_1 \cup D_2 \text{ where } D_1 & =\{x \in \mathbf{R}: x<0\} \text{ and } \\ & D_2=\{x \in \mathbf{R}: x>0\} \end{aligned} $
Case 1
If $\lim _{x \to c} f(x)=\lim _{x \to c}(x+2) \text= c + 2 = f (c)$ and hence $f$ is continuous in $D_1$
Case 2
$ If c \in D_2, then \lim _{x \to c} f(x)=\lim _{x \to c}(-x+2) =-c+2=f(c) $
and hence $f$ is continuous in $D_2$. Since $f$ is continuous at all points in the domain of $f$, we deduce that $f$ is continuous. Graph of this function is given in the Fig 5.6. Note that to graph this function we need to lift the pen from the plane
Fig 5.6 of the paper, but we need to do that only for those points where the function is not defined.
Example 13 Discuss the continuity of the function $f$ given by
$$ f(x)= \begin{cases}x, & \text { or } x \geq 0 \\ x^{2}, & \text { or } x<0\end{cases} $$
Solution Clearly the function is defined at every real number. Graph of the function is given in Fig 5.7. By inspection, it seems prudent to partition the domain of definition of $f$ into three disjoint subsets of the real line.
Let $\qquad \begin{aligned}& D_1={x \in \mathbf{R}: x<0}, D_2={0} \text{ and } \& D_3={x \in \mathbf{R}: x>0}\end{aligned}$
Fig 5.7
Case 1 At any point in $D_1$, we have $f(x)=x^{2}$ and it is easy to see that it is continuous there (see Example 2 ).
Case 2 At any point in $D_3$, we have $f(x)=x$ and it is easy to see that it is continuous there (see Example 6 ).
Case 3 Now we analyse the function at $x=0$. The value of the function at 0 is $f(0)=0$. The left hand limit of $f$ at 0 is
$$ \lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{-}} x^{2}=0^{2}=0 $$
The right hand limit of $f$ at 0 is
$$ \lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}} x=0 $$
Thus $\lim _{x \to 0} f(x)=0=f(0)$ and hence $f$ is continuous at 0 . This means that $f$ is continuous at every point in its domain and hence, $f$ is a continuous function.
Example 14 Show that every polynomial function is continuous.
Solution Recall that a function $p$ is a polynomial function if it is defined by $p(x)=a_0+a_1 x+\ldots+a_n x^{n}$ for some natural number $n, a_n \neq 0$ and $a_i \in \mathbf{R}$. Clearly this function is defined for every real number. For a fixed real number $c$, we have
$$ \lim _{x \to c} p(x)=p(c) $$
By definition, $p$ is continuous at $c$. Since $c$ is any real number, $p$ is continuous at every real number and hence $p$ is a continuous function.
Example 15 Find all the points of discontinuity of the greatest integer function defined by $f(x)=[x]$, where $[x]$ denotes the greatest integer less than or equal to $x$.
Solution First observe that $f$ is defined for all real numbers. Graph of the function is given in Fig 5.8. From the graph it looks like that $f$ is discontinuous at every integral point. Below we explore, if this is true.
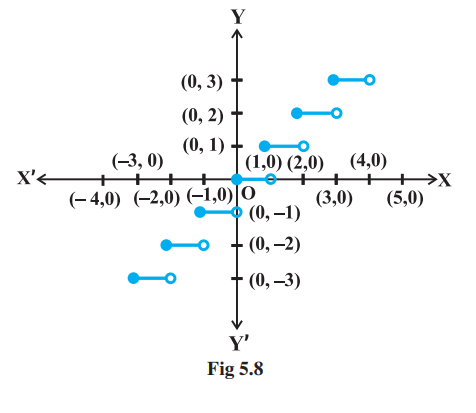
Fig 5.8
Case 1 Let $c$ be a real number which is not equal to any integer. It is evident from the graph that for all real numbers close to $c$ the value of the function is equal to $[c]$; i.e., $\lim _{x \to c} f(x)=\lim _{x \to c}[x]=[c]$. Also $f(c)=[c]$ and hence the function is continuous at all real numbers not equal to integers.
Case 2 Let $c$ be an integer. Then we can find a sufficiently small real number $r>0$ such that $[c-r]=c-1$ whereas $[c+r]=c$.
This, in terms of limits mean that
$$ \lim _{x \to c^{-}} f(x)=c-1, \lim _{x \to c^{+}} f(x)=c $$
Since these limits cannot be equal to each other for any $c$, the function is discontinuous at every integral point.
5.2.1 Algebra of continuous functions
In the previous class, after having understood the concept of limits, we learnt some algebra of limits. Analogously, now we will study some algebra of continuous functions. Since continuity of a function at a point is entirely dictated by the limit of the function at that point, it is reasonable to expect results analogous to the case of limits.
Theorem 1 Suppose $f$ and $g$ be two real functions continuous at a real number $c$. Then
(1) $f+g$ is continuous at $x=c$.
(2) $f-g$ is continuous at $x=c$.
(3) $f . g$ is continuous at $x=c$.
(4) $(\frac{f}{g})$ is continuous at $x=c$, (provided $g(c) \neq 0$).
Proof We are investigating continuity of $(f+g)$ at $x=c$. Clearly it is defined at $x=c$. We have
$ \begin{aligned} \lim _{x \to c}(f+g)(x) & =\lim _{x \to c}[f(x)+g(x)] & &( \text{ by definition of} f+g) \\ & =\lim _{x \to c} f(x)+\lim _{x \to c} g(x) & & \text{ (by the theorem on limits) } \\ & =f(c)+g(c) & & (\text{ as } f \text{ and } g \text{ are continuous }) \\ & =(f+g)(c) & & (\text{ by definition of } f+g) \end{aligned} $
Hence, $f+g$ is continuous at $x=c$.
Proofs for the remaining parts are similar and left as an exercise to the reader.
Remarks
(i) As a special case of (3) above, if $f$ is a constant function, i.e., $f(x)=\lambda$ for some real number $\lambda$, then the function $(\lambda . g)$ defined by $(\lambda . g)(x)=\lambda . g(x)$ is also continuous. In particular if $\lambda=-1$, the continuity of $f$ implies continuity of $-f$.
(ii) As a special case of (4) above, if $f$ is the constant function $f(x)=\lambda$, then the function $\frac{\lambda}{g}$ defined by $\frac{\lambda}{g}(x)=\frac{\lambda}{g(x)}$ is also continuous wherever $g(x) \neq 0$. In particular, the continuity of $g$ implies continuity of $\frac{1}{g}$.
The above theorem can be exploited to generate many continuous functions. They also aid in deciding if certain functions are continuous or not. The following examples illustrate this:
Example 16 Prove that every rational function is continuous.
Solution Recall that every rational function $f$ is given by
$$ f(x)=\frac{p(x)}{q(x)}, q(x) \neq 0 $$
where $p$ and $q$ are polynomial functions. The domain of $f$ is all real numbers except points at which $q$ is zero. Since polynomial functions are continuous (Example 14 ), $f$ is continuous by (4) of Theorem 1.
Example 17 Discuss the continuity of sine function.
Solution To see this we use the following facts
$$ \lim _{x \to 0} \sin x=0 $$
We have not proved it, but is intuitively clear from the graph of $\sin x$ near 0 .
Now, observe that $f(x)=\sin x$ is defined for every real number. Let $c$ be a real number. Put $x=c+h$. If $x \to c$ we know that $h \to 0$. Therefore
$$ \begin{aligned} \lim _{x \to c} f(x) & =\lim _{x \to c} \sin x \\ & =\lim _{h \to 0} \sin (c+h) \\ & =\lim _{h \to 0}[\sin c \cos h+\cos c \sin h] \\ & =\lim _{h \to 0}[\sin c \cos h]+\lim _{h \to 0}[\cos c \sin h] \\ & =\sin c+0=\sin c=f(c) \end{aligned} $$
Thus $\lim _{x \to c} f(x)=f(c)$ and hence $f$ is a continuous function.
Remark A similar proof may be given for the continuity of cosine function.
Example 18 Prove that the function defined by $f(x)=\tan x$ is a continuous function.
Solution The function $f(x)=\tan x=\frac{\sin x}{\cos x}$. This is defined for all real numbers such that $\cos x \neq 0$, i.e., $x \neq(2 n+1) \frac{\pi}{2}$. We have just proved that both sine and cosine functions are continuous. Thus $\tan x$ being a quotient of two continuous functions is continuous wherever it is defined.
An interesting fact is the behaviour of continuous functions with respect to composition of functions. Recall that if $f$ and $g$ are two real functions, then
$$ (f \circ g)(x)=f(g(x)) $$
is defined whenever the range of $g$ is a subset of domain of $f$. The following theorem (stated without proof) captures the continuity of composite functions. Theorem 2 Suppose $f$ and $g$ are real valued functions such that $(f \circ g)$ is defined at $c$. If $g$ is continuous at $c$ and if $f$ is continuous at $g(c)$, then $(f \circ g)$ is continuous at $c$.
The following examples illustrate this theorem.
Example 19 Show that the function defined by $f(x)=\sin (x^{2})$ is a continuous function.
Solution Observe that the function is defined for every real number. The function $f$ may be thought of as a composition $g$ o $h$ of the two functions $g$ and $h$, where $g(x)=\sin x$ and $h(x)=x^{2}$. Since both $g$ and $h$ are continuous functions, by Theorem 2, it can be deduced that $f$ is a continuous function.
Example 20 Show that the function $f$ defined by $ f(x)=|1-x+| x||, $
where $x$ is any real number, is a continuous function.
Solution Define $g$ by $g(x)=1-x+|x|$ and $h$ by $h(x)=|x|$ for all real $x$. Then
$$ \begin{aligned} (h \circ g)(x) & =h(g(x)) \\ & =h(1-x+|x|) \\ & =|1-x+| x||=f(x) \end{aligned} $$
In Example 7 , we have seen that $h$ is a continuous function. Hence $g$ being a sum of a polynomial function and the modulus function is continuous. But then $f$ being a composite of two continuous functions is continuous.
EXERCISE 5.1
1. Prove that the function $f(x)=5 x-3$ is continuous at $x=0$, at $x=-3$ and at $x=5$.
Show Answer
Solution
The given function is $f(x)=5 x-3$
At $x=0, f(0)=5 \times 0-3=3$
$\lim _{x \to 0} f(x)=\lim _{x \to 0}(5 x-3)=5 \times 0-3=-3$
$\therefore \lim _{x \to 0} f(x)=f(0)$
Therefore, $f$ is continuous at $x=0$
At $x=-3, f(-3)=5 \times(-3)-3=-18$
$\lim _{x \to-3} f(x)=\lim _{x \to-3}(5 x-3)=5 \times(-3)-3=-18$
$\therefore \lim _{x \to-3} f(x)=f(-3)$
Therefore, $f$ is continuous at $x=-3$
At $x=5, f(x)=f(5)=5 \times 5-3=25-3=22$
$\lim _{x \to 5} f(x)=\lim _{x \to 5}(5 x-3)=5 \times 5-3=22$
$\therefore \lim _{x \to 5} f(x)=f(5)$
Therefore, $f$ is continuous at $x=5$
2. Examine the continuity of the function $f(x)=2 x^{2}-1$ at $x=3$.
Show Answer
Solution
The given function is $f(x)=2 x^{2}-1$
At $x=3, f(x)=f(3)=2 \times 3^{2}-1=17$
$\lim _{x \to 3} f(x)=\lim _{x \to 3}(2 x^{2}-1)=2 \times 3^{2}-1=17$
$\therefore \lim _{x \to 3} f(x)=f(3)$
Thus, $f$ is continuous at $x=3$
3. Examine the following functions for continuity.
(a) $f(x)=x-5$
(b) $f(x)=\frac{1}{x-5}, x \neq 5$
(c) $f(x)=\frac{x^{2}-25}{x+5}, x \neq-5$
(d) $f(x)=|x-5|$
Show Answer
Solution
(a) The given function is $f(x)=x-5$
It is evident that $f$ is defined at every real number $k$ and its value at $k$ is $k-5$.
It is also observed that, $\lim _{x \to k} f(x)=\lim _{x \to k}(x-5)=k-5=f(k)$
$\therefore \lim _{x \to k} f(x)=f(k)$
Hence, $f$ is continuous at every real number and therefore, it is a continuous function.
(b) The given function is $f(x)=\frac{1}{x-5}, x \neq 5$
For any real number $k \neq 5$, we obtain
$\lim _{x \to k} f(x)=\lim _{x \to k} \frac{1}{x-5}=\frac{1}{k-5}$
Also, $f(k)=\frac{1}{k-5} \quad($ As $k \neq 5)$
$\therefore \lim _{x \to k} f(x)=f(k)$
Hence, $f$ is continuous at every point in the domain of $f$ and therefore, it is a continuous function.
(c) The given function is $f(x)=\frac{x^{2}-25}{x+5}, x \neq-5$
For any real number $c \neq-5$, we obtain
$ \begin{aligned} & \lim _{x \to c} f(x)=\lim _{x \to c} \frac{x^{2}-25}{x+5}=\lim _{x \to c} \frac{(x+5)(x-5)}{x+5}=\lim _{x \to c}(x-5)=(c-5) \\ & \text{ Also, } f(c)=\frac{(c+5)(c-5)}{c+5}=(c-5) \quad(\text{ as } c \neq-5) \\ & \therefore \lim _{x \to c} f(x)=f(c) \end{aligned} $
Hence, $f$ is continuous at every point in the domain of $f$ and therefore, it is a continuous function.
(d) The given function is $f(x)=|x-5|=\begin{cases} 5-x, \text{ if } x<5 \\ x-5, \text{ if } x \geq 5 \end{cases} .$
This function $f$ is defined at all points of the real line.
Let $c$ be a point on a real line. Then, $c<5$ or $c=5$ or $c>5$
Case I: $c<5$
Then, $f(c)=5-c$
$\lim _{x \to c} f(x)=\lim _{x \to c}(5-x)=5-c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all real numbers less than 5 .
Case II : $c=5$
Then, $f(c)=f(5)=(5-5)=0$
$\lim _{x \to 5^{-}} f(x)=\lim _{x \to 5}(5-x)=(5-5)=0$
$\lim _{x \to 5^{+}} f(x)=\lim _{x \to 5}(x-5)=0$
$\therefore \lim _{x \to c^{-}} f(x)=\lim _{x \to c^{+}} f(x)=f(c)$
Therefore, $f$ is continuous at $x=5$
Case III: $c>5$
Then, $f(c)=f(5)=c-5$
$\lim _{x \to c} f(x)=\lim _{x \to c}(x-5)=c-5$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all real numbers greater than 5 .
Hence, $f$ is continuous at every real number and therefore, it is a continuous function.
4. Prove that the function $f(x)=x^{n}$ is continuous at $x=n$, where $n$ is a positive integer.
Show Answer
Solution
The given function is $f(x)=x^{n}$
It is evident that $f$ is defined at all positive integers, $n$, and its value at $n$ is $n^{n}$.
Then, $\lim _{x \to n} f(n)=\lim _{x \to n}(x^{n})=n^{n}$
$\therefore \lim _{x \to n} f(x)=f(n)$
Therefore, $f$ is continuous at $n$, where $n$ is a positive integer.
5. Is the function $f$ defined by
$ f(x)= \begin{cases}x, & \text{ if } x \leq 1 \\ 5, & \text{ if } x>1\end{cases} $
continuous at $x=0$ ? At $x=1$ ? At $x=2$ ?
Show Answer
Solution
The given function $f$ is $f(x)= \begin{cases}x, & \text{ if } x \leq 1 \\ 5, & \text{ if } x>1\end{cases}$
At $x=0$,
It is evident that $f$ is defined at 0 and its value at 0 is 0 .
Then, $\lim _{x \to 0} f(x)=\lim _{x \to 0} x=0$
$\therefore \lim _{x \to 0} f(x)=f(0)$
Therefore, $f$ is continuous at $x=0$
At $x=1$,
$f$ is defined at 1 and its value at 1 is 1 .
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}} x=1$
The right hand limit of $f$ at $x=1$ is,
$ \begin{aligned} & \lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(5)=5 \\ & \therefore \lim _{x \to 1^{-}} f(x) \neq \lim _{x \to 1^{+}} f(x) \end{aligned} $
Therefore, $f$ is not continuous at $x=1$
At $x=2$,
$f$ is defined at 2 and its value at 2 is 5 .
Then, $\lim _{x \to 2} f(x)=\lim _{x \to 2}(5)=5$
$\therefore \lim _{x \to 2} f(x)=f(2)$
Therefore, $f$ is continuous at $x=2$
Find all points of discontinuity of $f$, where $f$ is defined by
6. $f(x)=\begin{cases}2 x+3, \text{ if } x \leq 2 \\ 2 x-3, \text{ if } x>2\end{cases}.$ $\quad\quad$
Show Answer
Solution
$ f(x)=\begin{cases} 2 x+3, \text{ if } x \leq 2 \\ 2 x-3, \text{ if } x>2 \end{cases} . $
It is evident that the given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line. Then, three cases arise.
(i) $c<2$
(ii) $c>2$
(iii) $c=2$
Case (i) $c<2$
Then, $f(c)=2 c+3$
$\lim _{x \to c} f(x)=\lim _{x \to c}(2 x+3)=2 c+3$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<2$
Case (ii) $c>2$
Then, $f(c)=2 c-3$
$\lim _{x \to c} f(x)=\lim _{x \to c}(2 x-3)=2 c-3$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>2$
Case (iii) $c=2$
Then, the left hand limit of $f$ at $x=2$ is,
$\lim _{x \to 2^{-}} f(x)=\lim _{x \to 2^{-}}(2 x+3)=2 \times 2+3=7$
The right hand limit of $f$ at $x=2$ is,
$\lim _{x \to 2^{+}} f(x)=\lim _{x \to 2^{+}}(2 x-3)=2 \times 2-3=1$
It is observed that the left and right hand limit of $f$ at $x=2$ do not coincide.
Therefore, $f$ is not continuous at $x=2$
Hence, $x=2$ is the only point of discontinuity of $f$.
7. $f(x)= \begin{cases}|x|+3, & \text{ if } x \leq-3 \\ -2 x, & \text{ if }-3<x<3 \\ 6 x+2, & \text{ if } x \geq 3\end{cases}$
Show Answer
Solution
$ f(x)=\begin{cases} |x|+3=-x+3, \text{ if } x \leq-3 \\ -2 x, \text{ if }-3<x<3 \\ 6 x+2, \text{ if } x \geq 3 \end{cases} . $
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<-3$, then $f(c)=-c+3$
$\lim _{x \to c} f(x)=\lim _{x \to c}(-x+3)=-c+3$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<-3$
Case II:
If $c=-3$, then $f(-3)=-(-3)+3=6$
$\lim _{x \to-3^{-}} f(x)=\lim _{x \to-3^{-}}(-x+3)=-(-3)+3=6$
$\lim _{x \to-3^{+}} f(x)=\lim _{x \to-3^{+}}(-2 x)=-2 \times(-3)=6$
$\therefore \lim _{x \to-3} f(x)=f(-3)$
Therefore, $f$ is continuous at $x=-3$
Case III:
If $-3<c<3$, then $f(c)=-2 c$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(-2 x)=-2 c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous in $(-3,3)$.
Case IV:
If $c=3$, then the left hand limit of $f$ at $x=3$ is,
$\lim _{x \to 3^{-}} f(x)=\lim _{x \to 3^{-}}(-2 x)=-2 \times 3=-6$
The right hand limit of $f$ at $x=3$ is,
$\lim _{x \to 3^{+}} f(x)=\lim _{x \to 3^{+}}(6 x+2)=6 \times 3+2=20$
It is observed that the left and right hand limit of $f$ at $x=3$ do not coincide.
Therefore, $f$ is not continuous at $x=3$
Case V:
If $c>3$, then $f(c)=6 c+2$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(6 x+2)=6 c+2$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>3$
Hence, $x=3$ is the only point of discontinuity of $f$.
8. $f(x)=\begin{cases}\frac{|x|}{x}, & \text{ if } x \neq 0 \\ 0, & \text{ if } x=0\end{cases}.$
Show Answer
Solution
$ f(x)=\begin{matrix} \frac{|x|}{x} \text{ if } x \neq 0 \\ 0, \text{ if } x=0 \end{matrix} . $
It is known that, $x<0 \Rightarrow|x|=-x$ and $x>0 \Rightarrow|x|=x$
Therefore, the given function can be rewritten as
$f(x)=\begin{cases} \frac{|x|}{x}=\frac{-x}{x}=-1 \text{ if } x<0 \\ 0, \text{ if } x=0 \\ \frac{|x|}{x}=\frac{x}{x}=1, \text{ if } x>0 \end{cases} .$
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<0$, then $f(c)=-1$
$\lim _{x \to c} f(x)=\lim _{x \to c}(-1)=-1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x<0$
Case II:
If $c=0$, then the left hand limit of $f$ at $x=0$ is,
$\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{-}}(-1)=-1$
The right hand limit of $f$ at $x=0$ is,
$\lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}}(1)=1$
It is observed that the left and right hand limit of $f$ at $x=0$ do not coincide.
Therefore, $f$ is not continuous at $x=0$
Case III:
If $c>0$, then $f(c)=1$
$\lim _{x \to c} f(x)=\lim _{x \to c}(1)=1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>0$
Hence, $x=0$ is the only point of discontinuity of $f$.
9. $f(x)= \begin{cases}\frac{x}{|x|}, & \text{ if } x<0 \\ -1, & \text{ if } x \geq 0\end{cases}$
Show Answer
Solution
$ f(x)=\begin{matrix} \frac{x}{|x|}, \text{ if } x<0 \\ -1, \text{ if } x \geq 0 \end{matrix} . $
It is known that, $x<0 \Rightarrow|x|=-x$
Therefore, the given function can be rewritten as
$f(x)=\begin{cases} \frac{x}{|x|}=\frac{x}{-x}=-1, \text{ if } x<0 \\ -1, \text{ if } x \geq 0 \end{cases} .$
$\Rightarrow f(x)=-1$ for all $x \in \mathbf{R}$
Let $c$ be any real number. Then, $\lim _{x \to c} f(x)=\lim _{x \to c}(-1)=-1$
Also, $f(c)=-1=\lim _{x \to c} f(x)$
Therefore, the given function is a continuous function.
Hence, the given function has no point of discontinuity.
10. $f(x)= \begin{cases}x+1, & \text{ if } x \geq 1 \\ x^{2}+1, & \text{ if } x<1\end{cases}$
Show Answer
Solution
$ f(x)=\begin{matrix} x+1, \text{ if } x \geq 1 \\ x^{2}+1, \text{ if } x<1 \end{matrix} . $
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<1$, then $f(c)=c^{2}+1$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x^{2}+1)=c^{2}+1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<1$
Case II:
If $c=1$, then $f(c)=f(1)=1+1=2$
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(x^{2}+1)=1^{2}+1=2$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(x+1)=1+1=2$
$\therefore \lim _{x \to 1} f(x)=f(1)$
Therefore, $f$ is continuous at $x=1$
Case III:
If $c>1$, then $f(c)=c+1$
$\lim _{x \to c} f(x)=\lim _{x \to c}(x+1)=c+1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>1$
Hence, the given function $f$ has no point of discontinuity.
11. $f(x)= \begin{cases}x^{3}-3, & \text{ if } x \leq 2 \\ x^{2}+1, & \text{ if } x>2\end{cases}$
Show Answer
Solution
$ f(x)=\begin{matrix} x^{3}-3, \text{ if } x \leq 2 \\ x^{2}+1, \text{ if } x>2 \end{matrix} . $
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<2$, then $f(c)=c^{3}-3$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x^{3}-3)=c^{3}-3$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<2$
Case II:
If $c=2$, then $f(c)=f(2)=2^{3}-3=5$
$\lim _{x \to 2^{-}} f(x)=\lim _{x \to 2^{-}}(x^{3}-3)=2^{3}-3=5$
$\lim _{x \to 2^{+}} f(x)=\lim _{x \to 2^{+}}(x^{2}+1)=2^{2}+1=5$
$\therefore \lim _{x \to 2} f(x)=f(2)$
Therefore, $f$ is continuous at $x=2$
Case III:
If $c>2$, then $f(c)=c^{2}+1$
$\lim _{x \to c} f(x)=\lim _{x \to c}(x^{2}+1)=c^{2}+1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>2$
Thus, the given function $f$ is continuous at every point on the real line.
Hence, $f$ has no point of discontinuity.
12. $f(x)= \begin{cases}x^{10}-1, & \text{ if } x \leq 1 \\ x^{2}, & \text{ if } x>1\end{cases}$
Show Answer
Solution
$ f(x)= \begin{cases}x^{10}-1, & \text{ if } x \leq 1 \\ x^{2}, & \text{ if } x>1\end{cases} $
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<1$, then $f(c)=c^{10}-1$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x^{10}-1)=c^{10}-1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<1$
Case II:
If $c=1$, then the left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(x^{10}-1)=1^{10}-1=1-1=0$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(x^{2})=1^{2}=1$
It is observed that the left and right hand limit of $f$ at $x=1$ do not coincide.
Therefore, $f$ is not continuous at $x=1$
Case III:
If $c>1$, then $f(c)=c^{2}$
$\lim _{x \to c} f(x)=\lim _{x \to c}(x^{2})=c^{2}$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>1$
Thus, from the above observation, it can be concluded that $x=1$ is the only point of discontinuity of $f$.
13. Is the function defined by $ f(x)= \begin{cases}x+5, & \text{ if } x \leq 1 \\ x-5, & \text{ if } x>1\end{cases} $ a continuous function?
Discuss the continuity of the function f, where f is defined by
Show Answer
Solution
The given function is $f(x)=\begin{cases} x+5, \text{ if } x \leq 1 \\ x-5, \text{ if } x>1 \end{cases} .$
The given function $f$ is defined at all the points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<1$, then $f(c)=c+5$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x+5)=c+5$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<1$
Case II:
If $c=1$, then $f(1)=1+5=6$
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(x+5)=1+5=6$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(x-5)=1-5=-4$
It is observed that the left and right hand limit of $f$ at $x=1$ do not coincide.
Therefore, $f$ is not continuous at $x=1$
Case III:
If $c>1$, then $f(c)=c-5$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x-5)=c-5$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>1$
Thus, from the above observation, it can be concluded that $x=1$ is the only point of discontinuity of $f$.
Discuss the continuity of the function $f$, where $f$ is defined by
14. $f(x)=\begin{cases} 3, \text{ if } 0 \leq x \leq 1 \\ 4, \text{ if } 1<x<3 \\ 5, \text{ if } 3 \leq x \leq 10\end{cases} .$
Show Answer
Solution
The given function is $f(x)=\begin{cases} 3, \text{ if } 0 \leq x \leq 1 \\ 4, \text{ if } 1<x<3 \\ 5, \text{ if } 3 \leq x \leq 10 \end{cases} .$
The given function is defined at all points of the interval $[0,10]$.
Let $c$ be a point in the interval $[0,10]$.
Case I:
If $0 \leq c<1$, then $f(c)=3$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(3)=3$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous in the interval $[0,1)$.
Case II:
If $c=1$, then $f(3)=3$
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(3)=3$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(4)=4$
It is observed that the left and right hand limits of $f$ at $x=1$ do not coincide.
Therefore, $f$ is not continuous at $x=1$
Case III:
If $1<c<3$, then $f(c)=4$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(4)=4$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points of the interval $(1,3)$.
Case IV:
If $c=3$, then $f(c)=5$
The left hand limit of $f$ at $x=3$ is,
$\lim _{x \to 3^{-}} f(x)=\lim _{x \to 3^{-}}(4)=4$
The right hand limit of $f$ at $x=3$ is,
$\lim _{x \to 3^{+}} f(x)=\lim _{x \to 3^{+}}(5)=5$
It is observed that the left and right hand limits of $f$ at $x=3$ do not coincide.
Therefore, $f$ is not continuous at $x=3$
Case V:
If $3<c \leq 10$, then $f(c)=5$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(5)=5$
$\lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points of the interval $(3,10]$.
Hence, $f$ is not continuous at $x=1$ and $x=3$
15. $f(x)= \begin{cases}2 x, & \text{ if } x<0 \\ 0, & \text{ if } 0 \leq x \leq 1 \\ 4 x, & \text{ if } x>1\end{cases}$
Show Answer
Solution
The given function is $f(x)= \begin{cases}2 x, & \text{ if } x<0 \\ 0, & \text{ if } 0 \leq x \leq 1 \\ 4 x, & \text{ if } x>1\end{cases}$
The given function is defined at all points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<0$, then $f(c)=2 c$
$\lim _{x \to c} f(x)=\lim _{x \to c}(2 x)=2 c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<0$
Case II:
If $c=0$, then $f(c)=f(0)=0$
The left hand limit of $f$ at $x=0$ is,
$\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{-}}(2 x)=2 \times 0=0$
The right hand limit of $f$ at $x=0$ is,
$\lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}}(0)=0$
$\therefore \lim _{x \to 0} f(x)=f(0)$
Therefore, $f$ is continuous at $x=0$
Case III:
If $0<c<1$, then $f(x)=0$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(0)=0$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points of the interval $(0,1)$.
Case IV:
If $c=1$, then $f(c)=f(1)=0$
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(0)=0$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}}(4 x)=4 \times 1=4$
It is observed that the left and right hand limits of $f$ at $x=1$ do not coincide.
Therefore, $f$ is not continuous at $x=1$
Case V:
If $c<1$, then $f(c)=4 c$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(4 x)=4 c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>1$
Hence, $f$ is not continuous only at $x=1$
16. $f(x)= \begin{cases}-2, & \text{ if } x \leq-1 \\ 2 x, & \text{ if }-1<x \leq 1 \\ 2, & \text{ if } x>1\end{cases}$
Show Answer
Solution
$ f(x)=\begin{matrix} -2, \text{ if } x \leq-1 \\ 2 x, \text{ if }-1<x \leq 1 \\ 2, \text{ if } x>1 \end{matrix} . $
The given function is defined at all points of the real line.
Let $c$ be a point on the real line.
Case I:
If $c<-1$, then $f(c)=-2$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(-2)=-2$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<-1$
Case II:
If $c=-1$, then $f(c)=f(-1)=-2$
The left hand limit of $f$ at $x=-1$ is,
$\lim _{x \to-1^{-}} f(x)=\lim _{x \to-1^{-}}(-2)=-2$
The right hand limit of $f$ at $x=-1$ is,
$ \begin{aligned} & \lim _{x \to-1^{+}} f(x)=\lim _{x \to-1^{+}}(2 x)=2 \times(-1)=-2 \\ & \therefore \lim _{x \to-1} f(x)=f(-1) \end{aligned} $
Therefore, $f$ is continuous at $x=-1$
Case III:
If $-1<c<1$, then $f(c)=2 c$
$\lim _{x \to c} f(x)=\lim _{x \to c}(2 x)=2 c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points of the interval $(-1,1)$.
Case IV:
If $c=1$, then $f(c)=f(1)=2 \times 1=2$
The left hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{-}} f(x)=\lim _{x \to 1^{-}}(2 x)=2 \times 1=2$
The right hand limit of $f$ at $x=1$ is,
$\lim _{x \to 1^{+}} f(x)=\lim _{x \to 1^{+}} 2=2$
$\therefore \lim _{x \to 1} f(x)=f(c)$
Therefore, $f$ is continuous at $x=2$
Case V:
If $c>1$, then $f(c)=2$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(2)=2$
$\lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>1$
Thus, from the above observations, it can be concluded that $f$ is continuous at all points of the real line.
17. Find the relationship between $a$ and $b$ so that the function $f$ defined by
$$ f(x)= \begin{cases}a x+1, & \text{ if } x \leq 3 \\ b x+3, & \text{ if } x>3\end{cases} $$
is continuous at $x=3$.
Show Answer
Solution
$ f(x)=\begin{matrix} a x+1, \text{ if } x \leq 3 \\ b x+3, \text{ if } x>3 \end{matrix} . $
If $f$ is continuous at $x=3$, then $\lim _{x \to 3^{-}} f(x)=\lim _{x \to 3^{+}} f(x)=f(3)$
Also,
$\lim _{x \to 3^{-}} f(x)=\lim _{x \to 3^{-}}(a x+1)=3 a+1$
$\lim _{x \to 3^{+}} f(x)=\lim _{x \to 3^{+}}(b x+3)=3 b+3$
$f(3)=3 a+1$
Therefore, from (1), we obtain
$3 a+1=3 b+3=3 a+1$
$\Rightarrow 3 a+1=3 b+3$
$\Rightarrow 3 a=3 b+2$
$\Rightarrow a=b+\frac{2}{3}$
Therefore, the required relationship is given by, $a=b+\frac{2}{3}$
18. For what value of $\lambda$ is the function defined by
$$ f(x)= \begin{cases}\lambda(x^{2}-2 x), & \text{ if } x \leq 0 \\ 4 x+1, & \text{ if } x>0\end{cases} $$
continuous at $x=0$ ? What about continuity at $x=1$ ?
Show Answer
Solution
The given function is $f(x)= \begin{cases}\lambda(x^{2}-2 x), & \text{ if } x \leq 0 \\ 4 x+1, & \text{ if } x>0\end{cases}$
If $f$ is continuous at $x=0$, then
$\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{+}} f(x)=f(0)$
$\Rightarrow \lim _{x \to 0^{-}} \lambda(x^{2}-2 x)=\lim _{x \to 0^{+}}(4 x+1)=\lambda(0^{2}-2 \times 0)$
$\Rightarrow \lambda(0^{2}-2 \times 0)=4 \times 0+1=0$
$\Rightarrow 0=1=0$, which is not possible
Therefore, there is no value of $\lambda$ for which $f$ is continuous at $x=0$
At $x=1$,
$f(1)=4 x+1=4 \times 1+1=5$
$\lim _{x \to 1}(4 x+1)=4 \times 1+1=5$
$\therefore \lim _{x \to 1} f(x)=f(1)$
Therefore, for any values of $\lambda, f$ is continuous at $x=1$
19. Show that the function defined by $g(x)=x-[x]$ is discontinuous at all integral points. Here $[x]$ denotes the greatest integer less than or equal to $x$.
Show Answer
Solution
The given function is $g(x)=x-[x]$
It is evident that $g$ is defined at all integral points.
Let $n$ be an integer.
Then,
$g(n)=n-[n]=n-n=0$
The left hand limit of $f$ at $x=n$ is,
$\lim _{x \to n^{-}} g(x)=\lim _{x \to n^{-}}(x-[x])=\lim _{x \to n^{-}}(x)-\lim _{x \to n^{-}}[x]=n-(n-1)=1$
The right hand limit of $f$ at $x=n$ is,
$\lim _{x \to n^{+}} g(x)=\lim _{x \to n^{+}}(x-[x])=\lim _{x \to n^{+}}(x)-\lim _{x \to n^{+}}[x]=n-n=0$
It is observed that the left and right hand limits of $f$ at $x=n$ do not coincide.
Therefore, $f$ is not continuous at $x=n$
Hence, $g$ is discontinuous at all integral points.
20. Is the function defined by f(x) = x2 – sin x + 5 continuous at x = π?
21. Discuss the continuity of the following functions:
(a) $f(x)=\sin x+\cos x$
(b) $f(x)=\sin x-\cos x$
(c) $f(x)=\sin x \cdot \cos x$
Show Answer
Solution
It is known that if $g$ and $h$ are two continuous functions, then
$g+h, g-h$, and $g . h$ are also continuous.
It has to proved first that $g(x)=\sin x$ and $h(x)=\cos x$ are continuous functions.
Let $g(x)=\sin x$
It is evident that $g(x)=\sin x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+h$
If $x \to c$, then $h \to 0$
$ \begin{aligned} & g(c)=\sin c \\ & \begin{aligned} \lim _{x \to c} g(x) & =\lim _{x \to c} \sin x \\ & =\lim _{h \to 0} \sin (c+h) \\ & =\lim _{h \to 0}[\sin c \cos h+\cos c \sin h] \\ & =\lim _{h \to 0}(\sin c \cos h)+\lim _{h \to 0}(\cos c \sin h) \\ & =\sin c \cos 0+\cos c \sin 0 \\ & =\sin c+0 \\ & =\sin c \end{aligned} \\ & \therefore \lim _{x \to c} g(x)=g(c) \end{aligned} $
Therefore, $g$ is a continuous function.
Let $h(x)=\cos x$
It is evident that $h(x)=\cos x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+h$
If $x \to c$, then $h \to 0$
$h(c)=\cos c$
$ \begin{aligned} \lim _{x \to c} h(x) & =\lim _{x \to c} \cos x \\ & =\lim _{h \to 0} \cos (c+h) \\ & =\lim _{h \to 0}[\cos c \cos h-\sin c \sin h] \\ & =\lim _{h \to 0} \cos c \cos h-\lim _{h \to 0} \sin c \sin h \\ & =\cos c \cos 0-\sin c \sin 0 \\ & =\cos c \times 1-\sin c \times 0 \\ & =\cos c \end{aligned} $
$\therefore \lim _{x \to c} h(x)=h(c)$
Therefore, $h$ is a continuous function.
Therefore, it can be concluded that
(a) $f(x)=g(x)+h(x)=\sin x+\cos x$ is a continuous function
(b) $f(x)=g(x)-h(x)=\sin x-\cos x$ is a continuous function
(c) $f(x)=g(x) \times h(x)=\sin x \times \cos x$ is a continuous function
22. Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Show Answer
Solution
It is known that if $g$ and $h$ are two continuous functions, then
(i) $\frac{h(x)}{g(x)}, g(x) \neq 0$ is continuous
(ii) $\frac{1}{g(x)}, g(x) \neq 0$ is continuous
(iii) $\frac{1}{h(x)}, h(x) \neq 0$ is continuous
It has to be proved first that $g(x)=\sin x$ and $h(x)=\cos x$ are continuous functions.
Let $g(x)=\sin x$
It is evident that $g(x)=\sin x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+h$
If $x \to c$, then $h \to 0$
$g(c)=\sin c$
$\lim _{x \to c} g(x)=\lim _{x \to c} \sin x$
$=\lim _{h \to 0} \sin (c+h)$
$=\lim _{h \to 0}[\sin c \cos h+\cos c \sin h]$
$=\lim _{h \to 0}(\sin c \cos h)+\lim _{h \to 0}(\cos c \sin h)$
$=\sin c \cos 0+\cos c \sin 0$
$=\sin c+0$
$=\sin c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is a continuous function.
Let $h(x)=\cos x$
It is evident that $h(x)=\cos x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+h$
If $x \to c$, then $h \to 0$
$h(c)=\cos c$
$ \begin{aligned} \lim _{x \to c} h(x) & =\lim _{x \to c} \cos x \\ & =\lim _{h \to 0} \cos (c+h) \\ & =\lim _{h \to 0}[\cos c \cos h-\sin c \sin h] \\ & =\lim _{h \to 0} \cos c \cos h-\lim _{h \to 0} \sin c \sin h \\ & =\cos c \cos 0-\sin c \sin 0 \\ & =\cos c \times 1-\sin c \times 0 \\ & =\cos c \end{aligned} $
$\therefore \lim _{x \to c} h(x)=h(c)$
Therefore, $h(x)=\cos x$ is continuous function.
It can be concluded that,
$cosec x=\frac{1}{\sin x}, \sin x \neq 0$ is continuous
$\Rightarrow cosec x, x \neq n \pi(n \in Z)$ is continuous
Therefore, cosecant is continuous except at $x=n p, n$ Î $\mathbf{Z}$
$\sec x=\frac{1}{\cos x}, \cos x \neq 0$ is continuous
$\Rightarrow \sec x, x \neq(2 n+1) \frac{\pi}{2}(n \in \mathbf{Z})$ is continuous
Therefore, secant is continuous except at $x=(2 n+1) \frac{\pi}{2}(n \in \mathbf{Z})$
$\cot x=\frac{\cos x}{\sin x}, \sin x \neq 0$ is continuous
$\Rightarrow \cot x, x \neq n \pi(n \in Z)$ is continuous
Therefore, cotangent is continuous except at $x=n p, n \hat{I} \mathbf{Z}$
23. Find all points of discontinuity of $f$, where
$$ f(x)= \begin{cases}\frac{\sin x}{x}, & \text{ if } x<0 \\ x+1, & \text{ if } x \geq 0\end{cases} $$
Show Answer
Solution
$ f(x)=\begin{cases} \frac{\sin x}{x}, \text{ if } x<0 \\ x+1, \text{ if } x \geq 0 \end{cases} . $
It is evident that $f$ is defined at all points of the real line.
Let $c$ be a real number.
Case I:
If $c<0$, then $f(c)=\frac{\sin c}{c}$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(\frac{\sin x}{x})=\frac{\sin c}{c}$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x<0$
Case II:
If $c>0$, then $f(c)=c+1$ and $\lim _{x \to c} f(x)=\lim _{x \to c}(x+1)=c+1$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x>0$
Case III:
If $c=0$, then $f(c)=f(0)=0+1=1$
The left hand limit of $f$ at $x=0$ is,
$\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0} \frac{\sin x}{x}=1$
The right hand limit of $f$ at $x=0$ is,
$ \begin{aligned} & \lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}}(x+1)=1 \\ & \therefore \lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{+}} f(x)=f(0) \end{aligned} $
Therefore, $f$ is continuous at $x=0$
From the above observations, it can be concluded that $f$ is continuous at all points of the real line.
Thus, $f$ has no point of discontinuity.
24. Determine if $f$ defined by
$$ f(x)= \begin{cases}x^{2} \sin \frac{1}{x}, & \text{ if } x \neq 0 \\ 0, & \text{ if } x=0\end{cases} $$
is a continuous function?
Show Answer
Solution
$ f(x)= \begin{cases}x^{2} \sin \frac{1}{x}, & \text{ if } x \neq 0 \\ 0, & \text{ if } x=0\end{cases} $
It is evident that $f$ is defined at all points of the real line.
Let $c$ be a real number.
Case I:
If $c \neq 0$, then $f(c)=c^{2} \sin \frac{1}{c}$
$\lim _{x \to c} f(x)=\lim _{x \to c}(x^{2} \sin \frac{1}{x})=(\lim _{x \to c} x^{2})(\lim _{x \to c} \sin \frac{1}{x})=c^{2} \sin \frac{1}{c}$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x \neq 0$
Case II:
If $c=0$, then $f(0)=0$ $\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{-}}(x^{2} \sin \frac{1}{x})=\lim _{x \to 0}(x^{2} \sin \frac{1}{x})$
It is known that, $-1 \leq \sin \frac{1}{x} \leq 1, x \neq 0$
$\Rightarrow-x^{2} \leq \sin \frac{1}{x} \leq x^{2}$
$\Rightarrow \lim _{x \to 0}(-x^{2}) \leq \lim _{x \to 0}(x^{2} \sin \frac{1}{x}) \leq \lim _{x \to 0} x^{2}$
$\Rightarrow 0 \leq \lim _{x \to 0}(x^{2} \sin \frac{1}{x}) \leq 0$
$\Rightarrow \lim _{x \to 0}(x^{2} \sin \frac{1}{x})=0$
$\therefore \lim _{x \to 0^{-}} f(x)=0$
Similarly, $\lim _{x \to 0^{+}} f(x)=\lim _{x \to 0^{+}}(x^{2} \sin \frac{1}{x})=\lim _{x \to 0}(x^{2} \sin \frac{1}{x})=0$
$\therefore \lim _{x \to 0^{-}} f(x)=f(0)=\lim _{x \to 0^{+}} f(x)$
Therefore, $f$ is continuous at $x=0$
From the above observations, it can be concluded that $f$ is continuous at every point of the real line.
Thus, $f$ is a continuous function.
25. Examine the continuity of $f$, where $f$ is defined by
$$ f(x)= \begin{cases}\sin x-\cos x, & \text{ if } x \neq 0 \\ -1, & \text{ if } x=0\end{cases} $$
Show Answer
Solution
$ f(x)= \begin{cases}\sin x-\cos x, & \text{ if } x \neq 0 \\ -1 & \text{ if } x=0\end{cases} $
It is evident that $f$ is defined at all points of the real line.
Let $c$ be a real number.
Case I:
If $c \neq 0$, then $f(c)=\sin c-\cos c$
$\lim _{x \to c} f(x)=\lim _{x \to c}(\sin x-\cos x)=\sin c-\cos c$
$\therefore \lim _{x \to c} f(x)=f(c)$
Therefore, $f$ is continuous at all points $x$, such that $x \neq 0$
Case II:
If $c=0$, then $f(0)=-1$
$\lim _{x \to 0^{-}} f(x)=\lim _{x \to 0}(\sin x-\cos x)=\sin 0-\cos 0=0-1=-1$
$\lim _{x \to 0^{+}} f(x)=\lim _{x \to 0}(\sin x-\cos x)=\sin 0-\cos 0=0-1=-1$
$\therefore \lim _{x \to 0^{-}} f(x)=\lim _{x \to 0^{+}} f(x)=f(0)$
Therefore, $f$ is continuous at $x=0$
From the above observations, it can be concluded that $f$ is continuous at every point of the real line.
Thus, $f$ is a continuous function.
Find the values of $k$ so that the function $f$ is continuous at the indicated point in Exercises 26 to 29.
26. $f(x)=\begin{cases}\frac{k \cos x}{\pi-2 x}, & \text{ if } x \neq \frac{\pi}{2} \\ 3, & \text{ if } x=\frac{\pi}{2}\end{cases} \quad.$ at $x=\frac{\pi}{2}$
Show Answer
Solution
$ f(x)= \begin{cases}\frac{k \cos x}{\pi-2 x}, & \text{ if } x \neq \frac{\pi}{2} \\ 3, & \text{ if } x=\frac{\pi}{2}\end{cases} $
The given function $f$ is continuous at $x=\frac{\pi}{2}$, if $f$ is defined at $x=\frac{\pi}{2}$ and if the value of the $f$ at $x=\frac{\pi}{2}$ equals the limit of $f$ at $x=\frac{\pi}{2}$.
It is evident that $f$ is defined at $x=\frac{\pi}{2}$ and $f(\frac{\pi}{2})=3$
$\lim _{x \to \frac{\pi}{2}} f(x)=\lim _{x \to \frac{\pi}{2}} \frac{k \cos x}{\pi-2 x}$
Put $x=\frac{\pi}{2}+h$
Then, $x \to \frac{\pi}{2} \Rightarrow h \to 0$
$\begin{aligned} \therefore \lim _{x \to \frac{\pi}{2}} f(x) & =\lim _{x \to \frac{\pi}{2}} \frac{k \cos x}{\pi-2 x}=\lim _{h \to 0} \frac{k \cos (\frac{\pi}{2}+h)}{\pi-2(\frac{\pi}{2}+h)} \\ & =k \lim _{h \to 0} \frac{-\sin h}{-2 h}=\frac{k}{2} \lim _{h \to 0} \frac{\sin h}{h}=\frac{k}{2} \cdot 1=\frac{k}{2}\end{aligned}$
$\therefore \lim _{x \to \frac{\pi}{2}} f(x)=f(\frac{\pi}{2})$
$\Rightarrow \frac{k}{2}=3$
$\Rightarrow k=6$
Therefore, the required value of $k$ is 6 .
27. $f(x)=\begin{cases}k x^{2}, & \text{ if } x \leq 2 \\ 3, & \text{ if } x>2\end{cases} \quad.$ at $x=2$
Show Answer
Solution
The given function is $f(x)= \begin{cases}k x^{2}, & \text{ if } x \leq 2 \\ 3, & \text{ if } x>2\end{cases}$
The given function $f$ is continuous at $x=2$, if $f$ is defined at $x=2$ and if the value of $f$ at $x=2$ equals the limit of $f$ at $x=2$
It is evident that $f$ is defined at $x=2$ and $f(2)=k(2)^{2}=4 k$
$ \begin{aligned} & \lim _{x \to 2^{-}} f(x)=\lim _{x \to 2^{+}} f(x)=f(2) \\ & \Rightarrow \lim _{x \to 2^{-}}(k x^{2})=\lim _{x \to 2^{+}}(3)=4 k \\ & \Rightarrow k \times 2^{2}=3=4 k \\ & \Rightarrow 4 k=3=4 k \\ & \Rightarrow 4 k=3 \\ & \Rightarrow k=\frac{3}{4} \end{aligned} $
Therefore, the required value of $k$ is $\frac{3}{4}$.
28. $f(x)=\begin{cases}k x+1, & \text{ if } x \leq \pi \\ \cos x, & \text{ if } x>\pi\end{cases} \quad.$ at $x=\pi$
Show Answer
Solution
The given function is $f(x)=\begin{cases} k x+1, \text{ if } x \leq \pi \\ \cos x, \text{ if } x>\pi \end{cases} .$
The given function $f$ is continuous at $x=p$, if $f$ is defined at $x=p$ and if the value of $f$ at $x=p$ equals the limit of $f$ at $x=p$
It is evident that $f$ is defined at $x=p$ and $f(\pi)=k \pi+1$
$ \begin{aligned} & \lim _{x \to \pi^{-}} f(x)=\lim _{x \to \pi^{+}} f(x)=f(\pi) \\ & \Rightarrow \lim _{x \to \pi^{-}}(k x+1)=\lim _{x \to \pi^{+}} \cos x=k \pi+1 \\ & \Rightarrow k \pi+1=\cos \pi=k \pi+1 \\ & \Rightarrow k \pi+1=-1=k \pi+1 \\ & \Rightarrow k=-\frac{2}{\pi} \end{aligned} $
Therefore, the required value of $k$ is $-\frac{2}{\pi}$.
29. $f(x)=\begin{cases}k x+1, & \text{ if } x \leq 5 \\ 3 x-5, & \text{ if } x>5\end{cases} \quad.$ at $x=5$
Show Answer
Solution
$ f(x)=\begin{cases} k x+1, \text{ if } x \leq 5 \\ 3 x-5, \text{ if } x>5 \end{cases} . $
The given function $f$ is continuous at $x=5$, if $f$ is defined at $x=5$ and if the value of $f$ at $x=5$ equals the limit of $f$ at $x=5$
It is evident that $f$ is defined at $x=5$ and $f(5)=k x+1=5 k+1$
$ \begin{aligned} & \lim _{x \to 5^{-}} f(x)=\lim _{x \to 5^{+}} f(x)=f(5) \\ & \Rightarrow \lim _{x \to 5^{-}}(k x+1)=\lim _{x \to 5^{+}}(3 x-5)=5 k+1 \\ & \Rightarrow 5 k+1=15-5=5 k+1 \\ & \Rightarrow 5 k+1=10 \\ & \Rightarrow 5 k=9 \\ & \Rightarrow k=\frac{9}{5} \end{aligned} $
Therefore, the required value of $k$ is $\frac{9}{5}$.
30. Find the values of $a$ and $b$ such that the function defined by
$$ f(x)= \begin{cases}5, & \text{ if } x \leq 2 \\ a x+b, & \text{ if } 2<x<10 \\ 21, & \text{ if } x \geq 10\end{cases} $$
is a continuous function.
Show Answer
Solution
$ f(x)= \begin{cases}5, & \text{ if } x \leq 2 \\ a x+b, & \text{ if } 2<x<10 \\ 21, & \text{ if } x \geq 10\end{cases} $
It is evident that the given function $f$ is defined at all points of the real line.
If $f$ is a continuous function, then $f$ is continuous at all real numbers.
In particular, $f$ is continuous at $x=2$ and $x=10$
Since $f$ is continuous at $x=2$, we obtain
$ \begin{aligned} & \lim _{x \to 2^{-}} f(x)=\lim _{x \to 2^{+}} f(x)=f(2) \\ & \Rightarrow \lim _{x \to 2^{-}}(5)=\lim _{x \to 2^{+}}(a x+b)=5 \\ & \Rightarrow 5=2 a+b=5 \\ & \Rightarrow 2 a+b=5 \\ \end{aligned} $
Since $f$ is continuous at $x=10$, we obtain
$$ \begin{align*} & \lim _{x \to 10^{-}} f(x)=\lim _{x \to 10^{+}} f(x)=f(10) \\ & \Rightarrow \lim _{x \to 10^{-}}(a x+b)=\lim _{x \to 10^{+}}(21)=21 \\ & \Rightarrow 10 a+b=21=21 \\ & \Rightarrow 10 a+b=21 \tag{2} \end{align*} $$
On subtracting equation (1) from equation (2), we obtain
$8 a=16$
$\Rightarrow a=2$
By putting $a=2$ in equation (1), we obtain
$2 \times 2+b=5$
$\Rightarrow 4+b=5$ $\Rightarrow b=1$
Therefore, the values of $a$ and $b$ for which $f$ is a continuous function are 2 and 1 respectively.
31. Show that the function defined by $f(x)=\cos (x^{2})$ is a continuous function.
Show Answer
Solution
The given function is $f(x)=\cos (x^{2})$
This function $f$ is defined for every real number and $f$ can be written as the composition of two functions as,
$f=g \circ h$, where $g(x)=\cos x$ and $h(x)=x^{2}$
$[\because(g \circ h)(x)=g(h(x))=g(x^{2})=\cos (x^{2})=f(x)]$
It has to be first proved that $g(x)=\cos x$ and $h(x)=x^{2}$ are continuous functions.
It is evident that $g$ is defined for every real number.
Let $c$ be a real number.
Then, $g(c)=\cos c$
Put $x=c+h$
If $x \to c$, then $h \to 0$
$\lim _{x \to c} g(x)=\lim _{x \to c} \cos x$
$=\lim _{h \to 0} \cos (c+h)$
$=\lim _{h \to 0}[\cos c \cos h-\sin c \sin h]$
$=\lim _{h \to 0} \cos c \cos h-\lim _{h \to 0} \sin c \sin h$
$=\cos c \cos 0-\sin c \sin 0$
$=\cos c \times 1-\sin c \times 0$
$=\cos c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g(x)=\cos x$ is continuous function. $h(x)=x^{2}$
Clearly, $h$ is defined for every real number.
Let $k$ be a real number, then $h(k)=k^{2}$
$\lim _{x \to k} h(x)=\lim _{x \to k} x^{2}=k^{2}$
$\therefore \lim _{x \to k} h(x)=h(k)$
Therefore, $h$ is a continuous function.
It is known that for real valued functions $g$ and $h$, such that $(g \circ h)$ is defined at $c$, if $g$ is continuous at $c$ and if $f$ is continuous at $g(c)$, then $(f \circ g)$ is continuous at $c$.
Therefore, $f(x)=(g o h)(x)=\cos (x^{2})$ is a continuous function.
32. Show that the function defined by $f(x)=|\cos x|$ is a continuous function.
Show Answer
Solution
The given function is $f(x)=|\cos x|$
This function $f$ is defined for every real number and $f$ can be written as the composition of two functions as,
$f=g \circ h$, where $g(x)=|x|$ and $h(x)=\cos x$
$[\because(g \circ h)(x)=g(h(x))=g(\cos x)=|\cos x|=f(x)]$
It has to be first proved that $g(x)=|x|$ and $h(x)=\cos x$ are continuous functions.
$g(x)=|x|$ can be written as
$g(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases}$
Clearly, $g$ is defined for all real numbers.
Let $c$ be a real number.
Case I:
If $c<0$, then $g(c)=-c$ and $\lim _{x \to c} g(x)=\lim _{x \to c}(-x)=-c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x<0$
Case II:
If $c>0$, then $g(c)=c$ and $\lim _{x \to c} g(x)=\lim _{x \to c} x=c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x>0$
Case III:
If $c=0$, then $g(c)=g(0)=0$
$ \begin{aligned} & \lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{-}}(-x)=0 \\ & \lim _{x \to 0^{+}} g(x)=\lim _{x \to 0^{+}}(x)=0 \\ & \therefore \lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{+}}(x)=g(0) \end{aligned} $
Therefore, $g$ is continuous at $x=0$
From the above three observations, it can be concluded that $g$ is continuous at all points.
$h(x)=\cos x$
It is evident that $h(x)=\cos x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+h$
If $x \to c$, then $h \to 0$
$h(c)=\cos c$
$ \begin{aligned} \lim _{x \to c} h(x) & =\lim _{x \to c} \cos x \\ & =\lim _{h \to 0} \cos (c+h) \\ & =\lim _{h \to 0}[\cos c \cos h-\sin c \sin h] \\ & =\lim _{h \to 0} \cos c \cos h-\lim _{h \to 0} \sin c \sin h \\ & =\cos c \cos 0-\sin c \sin 0 \\ & =\cos c \times 1-\sin c \times 0 \\ & =\cos c \end{aligned} $
$\therefore \lim _{x \to c} h(x)=h(c)$
Therefore, $h(x)=\cos x$ is a continuous function.
It is known that for real valued functions $g$ and $h$, such that $(g \circ h)$ is defined at $c$, if $g$ is continuous at $c$ and if $f$ is continuous at $g(c)$, then $(f \circ g)$ is continuous at $c$.
Therefore, $f(x)=(g \circ h)(x)=g(h(x))=g(\cos x)=|\cos x|$ is a continuous function.
33. Examine that $\sin |x|$ is a continuous function.
Show Answer
Solution
Let $f(x)=\sin |x|$
This function $f$ is defined for every real number and $f$ can be written as the composition of two functions as,
$f=g \circ h$, where $g(x)=|x|$ and $h(x)=\sin x$
$[\because(g \circ h)(x)=g(h(x))=g(\sin x)=|\sin x|=f(x)]$
It has to be proved first that $g(x)=|x|$ and $h(x)=\sin x$ are continuous functions.
$g(x)=|x|$ can be written as
$g(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases}$
Clearly, $g$ is defined for all real numbers.
Let $c$ be a real number.
Case I:
If $c<0$, then $g(c)=-c$ and $\lim _{x \to c} g(x)=\lim _{x \to c}(-x)=-c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x<0$
Case II:
If $c>0$, then $g(c)=c$ and $\lim _{x \to c} g(x)=\lim _{x \to c} x=c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x>0$
Case III:
If $c=0$, then $g(c)=g(0)=0$
$ \begin{aligned} & \lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{-}}(-x)=0 \\ & \lim _{x \to 0^{+}} g(x)=\lim _{x \to 0^{+}}(x)=0 \\ & \therefore \lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{+}}(x)=g(0) \end{aligned} $
Therefore, $g$ is continuous at $x=0$
From the above three observations, it can be concluded that $g$ is continuous at all points.
$h(x)=\sin x$
It is evident that $h(x)=\sin x$ is defined for every real number.
Let $c$ be a real number. Put $x=c+k$
If $x \to c$, then $k \to 0$
$h(c)=\sin c$
$h(c)=\sin c$
$ \begin{aligned} \lim _{x \to c} h(x) & =\lim _{x \to c} \sin x \\ & =\lim _{k \to 0} \sin (c+k) \\ & =\lim _{k \to 0}[\sin c \cos k+\cos c \sin k] \\ & =\lim _{k \to 0}(\sin c \cos k)+\lim _{h \to 0}(\cos c \sin k) \\ & =\sin c \cos 0+\cos c \sin 0 \\ & =\sin c+0 \\ & =\sin c \end{aligned} $
$\therefore \lim _{x \to c} h(x)=g(c)$
Therefore, $h$ is a continuous function.
It is known that for real valued functions $g$ and $h$, such that $(g \circ h)$ is defined at $c$, if $g$ is continuous at $c$ and if $f$ is continuous at $g(c)$, then $(f \circ g)$ is continuous at $c$.
Therefore, $f(x)=(g \circ h)(x)=g(h(x))=g(\sin x)=|\sin x|$ is a continuous function.
34. Find all the points of discontinuity of $f$ defined by $f(x)=|x|-|x+1|$.
Show Answer
Solution
The given function is $f(x)=|x|-|x+1|$
The two functions, $g$ and $h$, are defined as
$g(x)=|x|$ and $h(x)=|x+1|$
Then, $f=g-h$
The continuity of $g$ and $h$ is examined first.
$g(x)=|x|$ can be written as
$g(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases}$
Clearly, $g$ is defined for all real numbers.
Let $c$ be a real number.
Case I:
If $c<0$, then $g(c)=-c$ and $\lim _{x \to c} g(x)=\lim _{x \to c}(-x)=-c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x<0$
Case II:
If $c>0$, then $g(c)=c$ and $\lim _{x \to c} g(x)=\lim _{x \to c} x=c$
$\therefore \lim _{x \to c} g(x)=g(c)$
Therefore, $g$ is continuous at all points $x$, such that $x>0$
Case III:
If $c=0$, then $g(c)=g(0)=0$
$\lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{-}}(-x)=0$
$\lim _{x \to 0^{+}} g(x)=\lim _{x \to 0^{+}}(x)=0$
$\therefore \lim _{x \to 0^{-}} g(x)=\lim _{x \to 0^{+}}(x)=g(0)$
Therefore, $g$ is continuous at $x=0$
From the above three observations, it can be concluded that $g$ is continuous at all points.
$h(x)=|x+1|$ can be written as
$h(x)= \begin{cases}-(x+1), & \text{ if, } x<-1 \\ x+1, & \text{ if } x \geq-1\end{cases}$
Clearly, $h$ is defined for every real number.
Let $c$ be a real number.
Case I:
If $c<-1$, then $h(c)=-(c+1)$ and $\lim _{x \to c} h(x)=\lim _{x \to c}[-(x+1)]=-(c+1)$
$\therefore \lim _{x \to c} h(x)=h(c)$
Therefore, $h$ is continuous at all points $x$, such that $x<-1$
Case II:
If $c>-1$, then $h(c)=c+1$ and $\lim _{x \to c} h(x)=\lim _{x \to c}(x+1)=c+1$
$\therefore \lim _{x \to c} h(x)=h(c)$
Therefore, $h$ is continuous at all points $x$, such that $x>-1$
Case III:
If $c=-1$, then $h(c)=h(-1)=-1+1=0$
$\lim _{x \to-1^{-}} h(x)=\lim _{x \to-1^{-}}[-(x+1)]=-(-1+1)=0$
$\lim _{x \to-1^{+}} h(x)=\lim _{x \to-1^{+}}(x+1)=(-1+1)=0$
$\therefore \lim _{x \to-1^{-}} h(x)=\lim _{h \to-1^{+}} h(x)=h(-1)$
Therefore, $h$ is continuous at $x=-1$
From the above three observations, it can be concluded that $h$ is continuous at all points of the real line.
$g$ and $h$ are continuous functions. Therefore, $f=g-h$ is also a continuous function.
Therefore, $f$ has no point of discontinuity.
5.3 Differentiability
Recall the following facts from previous class. We had defined the derivative of a real function as follows:
Suppose $f$ is a real function and $c$ is a point in its domain. The derivative of $f$ at $c$ is defined by
$$ \lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h} $$
provided this limit exists. Derivative of $f$ at $c$ is denoted by $f^{\prime}(c)$ or $.\frac{d}{d x}(f(x))| _{c}$. The function defined by
$$ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
wherever the limit exists is defined to be the derivative of $f$. The derivative of $f$ is denoted by $f^{\prime}(x)$ or $\frac{d}{d x}(f(x))$ or if $y=f(x)$ by $\frac{d y}{d x}$ or $y^{\prime}$. The process of finding derivative of a function is called differentiation. We also use the phrase differentiate $f(x)$ with respect to $x$ to mean find $f^{\prime}(x)$.
The following rules were established as a part of algebra of derivatives:
(1) $(u \pm v)^{\prime}=u^{\prime} \pm v^{\prime}$
(2) $(u v)^{\prime}=u^{\prime} v+u v^{\prime}$ (Leibnitz or product rule)
(3) $(\frac{u}{v})^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$, wherever $v \neq 0$ (Quotient rule).
The following table gives a list of derivatives of certain standard functions:
Table 5.3
| $ f $(x) | $ x^n $ | $ sin x $ | $ cos x $ | $ tanx $ |
|---|---|---|---|---|
| $ f $’(x) | $ nx^{n-1}$ | $ cos x $ | $ -sin x $ | sec^2 x |
Whenever we defined derivative, we had put a caution provided the limit exists. Now the natural question is; what if it doesn’t? The question is quite pertinent and so is its answer. If $\lim _{h \to 0} \frac{f(c+h)-f(c)}{h}$ does not exist, we say that $f$ is not differentiable at $c$. In other words, we say that a function $f$ is differentiable at a point $c$ in its domain if both $\lim _{h \to 0^{-}} \frac{f(c+h)-f(c)}{h}$ and $\lim _{h \to 0^{+}} \frac{f(c+h)-f(c)}{h}$ are finite and equal. A function is said to be differentiable in an interval $[a, b]$ if it is differentiable at every point of $[a, b]$. As in case of continuity, at the end points $a$ and $b$, we take the right hand limit and left hand limit, which are nothing but left hand derivative and right hand derivative of the function at $a$ and $b$ respectively. Similarly, a function is said to be differentiable in an interval $(a, b)$ if it is differentiable at every point of $(a, b)$.
Theorem 3 If a function $f$ is differentiable at a point $c$, then it is also continuous at that point.
Proof Since $f$ is differentiable at $c$, we have
$$ \lim _{x \rightarrow c} \frac{f(x)-f(c)}{x-c}=f^{\prime}(c) $$
But for $x \neq c$, we have
$$ f(x)-f(c)=\frac{f(x)-f(c)}{x-c} .(x-c) $$
$ \text{ Therefore } \qquad \begin{aligned} \lim _{x \to c}[f(x)-f(c)] & =\lim _{x \to c}[\frac{f(x)-f(c)}{x-c} \cdot(x-c)] \\ \lim _{x \to c}[f(x)]-\lim _{x \to c}[f(c)] & =\lim _{x \to c}[\frac{f(x)-f(c)}{x-c}] \cdot \lim _{x \to c}[(x-c)] \\ & =f^{\prime}(c) \cdot 0=0 \\ \lim _{x \to c} f(x) & =f(c) \end{aligned} $
Hence $f$ is continuous at $x=c$.
Corollary 1 Every differentiable function is continuous.
We remark that the converse of the above statement is not true. Indeed we have seen that the function defined by $f(x)=|x|$ is a continuous function. Consider the left hand limit
$$ \begin{aligned} \lim _{h \to 0^{-}} \frac{f(0+h)-f(0)}{h}=\frac{-h}{h}=-1 \end{aligned} $$
The right hand limit
$$ \begin{aligned} \lim _{h \to 0^{+}} \frac{f(0+h)-f(0)}{h}=\frac{h}{h}=1 \end{aligned} $$
Since the above left and right hand limits at 0 are not equal, $\lim _{h \to 0} \frac{f(0+h)-f(0)}{h}$ does not exist and hence $f$ is not differentiable at 0 . Thus $f$ is not a differentiable function.
5.3.1 Derivatives of composite functions
To study derivative of composite functions, we start with an illustrative example. Say, we want to find the derivative of $f$, where
$$ f(x)=(2 x+1)^{3} $$
One way is to expand $(2 x+1)^{3}$ using binomial theorem and find the derivative as a polynomial function as illustrated below.
$$ \begin{aligned} \frac{d}{d x} f(x) & =\frac{d}{d x}[(2 x+1)^{3}] \\ & =\frac{d}{d x}(8 x^{3}+12 x^{2}+6 x+1) \\ & =24 x^{2}+24 x+6 \\ & =6(2 x+1)^{2} \end{aligned} $$
Now, observe that
$$ f(x)=(h \circ g)(x) $$
where $g(x)=2 x+1$ and $h(x)=x^{3}$. Put $t=g(x)=2 x+1$. Then $f(x)=h(t)=t^{3}$.
$\text{ Thus }\frac{d f}{d x}=6(2 x+1)^{2}=3(2 x+1)^{2} \cdot 2=3 t^{2} \cdot 2=\frac{d h}{dt} \cdot \frac{d t}{d x}$
The advantage with such observation is that it simplifies the calculation in finding the derivative of, say, $(2 x+1)^{100}$. We may formalise this observation in the following theorem called the chain rule.
Theorem 4 (Chain Rule) Let $f$ be a real valued function which is a composite of two functions $u$ and $v$; i.e., $f=v$ o $u$. Suppose $t=u(x)$ and if both $\frac{d t}{d x}$ and $\frac{d v}{d t}$ exist, we have
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x} $$
We skip the proof of this theorem. Chain rule may be extended as follows. Suppose $f$ is a real valued function which is a composite of three functions $u, v$ and $w$; i.e.,
$$ \begin{aligned} & f=(w \circ u) \circ v \text{. If} t=v(x) \text{ and } s=u(t), then \\ & \frac{d f}{d x}=\frac{d}{d t}(w \circ u) \cdot \frac{d t}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x} \end{aligned} $$
provided all the derivatives in the statement exist. Reader is invited to formulate chain rule for composite of more functions.
Example 21 Find the derivative of the function given by $f(x)=\sin (x^{2})$.
Solution Observe that the given function is a composite of two functions. Indeed, if $t=u(x)=x^{2}$ and $v(t)=\sin t$, then
$ f(x)=(\begin{matrix} v & \circ & u \end{matrix} )(x)=v(u(x))=v(x^{2})=\sin x^{2} $ Put $t=u(x)=x^{2}$. Observe that $\frac{d v}{d t}=\cos t$ and $\frac{d t}{d x}=2 x$ exist. Hence, by chain rule
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=\cos t .2 x $$
It is normal practice to express the final result only in terms of $x$. Thus
$$ \frac{d f}{d x}=\cos t \cdot 2 x=2 x \cos x^{2} $$
EXERCISE 5.2
Differentiate the functions with respect to $x$ in Exercises 1 to 8 .
1. $\sin (x^{2}+5)$
Show Answer
Solution
Let $f(x)=\sin (x^{2}+5), u(x)=x^{2}+5$, and $v(t)=\sin t$
Then, $($ vou $)(x)=v(u(x))=v(x^{2}+5)=\tan (x^{2}+5)=f(x)$
Thus, $f$ is a composite of two functions.
Put $t=u(x)=x^{2}+5$
Then, we obtain
$\frac{d v}{d t}=\frac{d}{d t}(\sin t)=\cos t=\cos (x^{2}+5)$
$\frac{d t}{d x}=\frac{d}{d x}(x^{2}+5)=\frac{d}{d x}(x^{2})+\frac{d}{d x}(5)=2 x+0=2 x$
Therefore, by chain rule, $\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=\cos (x^{2}+5) \times 2 x=2 x \cos (x^{2}+5)$
Alternate method
$ \begin{aligned} \frac{d}{d x}[\sin (x^{2}+5)] & =\cos (x^{2}+5) \cdot \frac{d}{d x}(x^{2}+5) \\ & =\cos (x^{2}+5) \cdot[\frac{d}{d x}(x^{2})+\frac{d}{d x}(5)] \\ & =\cos (x^{2}+5) \cdot[2 x+0] \\ & =2 x \cos (x^{2}+5) \end{aligned} $
2. $\cos (\sin x)$
Show Answer
Solution
Let $f(x)=\cos (\sin x), u(x)=\sin x$, and $v(t)=\cos t$
Then, $($ vou $)(x)=v(u(x))=v(\sin x)=\cos (\sin x)=f(x)$
Thus, $f$ is a composite function of two functions.
Put $t=u(x)=\sin x$
$\therefore \frac{d v}{d t}=\frac{d}{d t}[\cos t]=-\sin t=-\sin (\sin x)$
$\frac{d t}{d x}=\frac{d}{d x}(\sin x)=\cos x$
By chain rule, $\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=-\sin (\sin x) \cdot \cos x=-\cos x \sin (\sin x)$
Alternate method
$\frac{d}{d x}[\cos (\sin x)]=-\sin (\sin x) \cdot \frac{d}{d x}(\sin x)=-\sin (\sin x) \cdot \cos x=-\cos x \sin (\sin x)$
3. $\sin (a x+b)$
Show Answer
Solution
Let $f(x)=\sin (a x+b), u(x)=a x+b$, and $v(t)=\sin t$
Then, $($ vou $)(x)=v(u(x))=v(a x+b)=\sin (a x+b)=f(x)$
Thus, $f$ is a composite function of two functions, $u$ and $v$.
Put $t=u(x)=a x+b$
Therefore,
$\frac{d v}{d t}=\frac{d}{d t}(\sin t)=\cos t=\cos (a x+b)$
$\frac{d t}{d x}=\frac{d}{d x}(a x+b)=\frac{d}{d x}(a x)+\frac{d}{d x}(b)=a+0=a$
Hence, by chain rule, we obtain
$\frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=\cos (a x+b) \cdot a=a \cos (a x+b)$
Alternate method
$ \begin{aligned} \frac{d}{d x}[\sin (a x+b)] & =\cos (a x+b) \cdot \frac{d}{d x}(a x+b) \\ & =\cos (a x+b) \cdot[\frac{d}{d x}(a x)+\frac{d}{d x}(b)] \\ & =\cos (a x+b) \cdot(a+0) \\ & =a \cos (a x+b) \end{aligned} $
4. $\sec (\tan (\sqrt{x}))$
Show Answer
Solution
Let $f(x)=\sec (\tan \sqrt{x}), u(x)=\sqrt{x}, v(t)=\tan t$, and $w(s)=\sec s$
Then, $($ wovou $)(x)=w[v(u(x))]=w[v(\sqrt{x})]=w(\tan \sqrt{x})=\sec (\tan \sqrt{x})=f(x)$
Thus, $f$ is a composite function of three functions, $u, v$, and $w$.
Put $s=v(t)=\tan t$ and $t=u(x)=\sqrt{x}$
$ \text{ Then, } \begin{aligned} \frac{d w}{d s} & =\frac{d}{d s}(\sec s)=\sec s \tan s=\sec (\tan t) \cdot \tan (\tan t) & & {[s=\tan t] } \\ & =\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) & & {[t=\sqrt{x}] } \end{aligned} $
$\frac{d s}{d t}=\frac{d}{d t}(\tan t)=\sec ^{2} t=\sec ^{2} \sqrt{x}$
$\frac{d t}{d x}=\frac{d}{d x}(\sqrt{x})=\frac{d}{d x}(x^{\frac{1}{2}})=\frac{1}{2} \cdot x^{\frac{1}{2}-1}=\frac{1}{2 \sqrt{x}}$
Hence, by chain rule, we obtain
$ \begin{aligned} & \frac{d t}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x} \\ & =\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \times \sec ^{2} \sqrt{x} \times \frac{1}{2 \sqrt{x}} \\ & =\frac{1}{2 \sqrt{x}} \sec ^{2} \sqrt{x} \sec (\tan \sqrt{x}) \tan (\tan \sqrt{x}) \\ & =\frac{\sec ^{2} \sqrt{x} \sec (\tan \sqrt{x}) \tan (\tan \sqrt{x})}{2 \sqrt{x}} \end{aligned} $
Alternate method
$ \begin{aligned} \frac{d}{d x}[\sec (\tan \sqrt{x})] & =\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \cdot \frac{d}{d x}(\tan \sqrt{x}) \\ & =\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \cdot \sec ^{2}(\sqrt{x}) \cdot \frac{d}{d x}(\sqrt{x}) \\ & =\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \cdot \sec ^{2}(\sqrt{x}) \cdot \frac{1}{2 \sqrt{x}} \\ & =\frac{\sec (\tan \sqrt{x}) \cdot \tan (\tan \sqrt{x}) \sec ^{2}(\sqrt{x})}{2 \sqrt{x}} \end{aligned} $
5. $\frac{\sin (a x+b)}{\cos (c x+d)}$
Show Answer
Solution
The given function is $f(x)=\frac{\sin (a x+b)}{\cos (c x+d)}=\frac{g(x)}{h(x)}$, where $g(x)=\sin (a x+b)$ and
$h(x)=\cos (c x+d)$
$\therefore f^{\prime}=\frac{g^{\prime} h-g h^{\prime}}{h^{2}}$
Consider $g(x)=\sin (a x+b)$
Let $u(x)=a x+b, v(t)=\sin t$
Then, $($ vou $)(x)=v(u(x))=v(a x+b)=\sin (a x+b)=g(x)$ $\therefore g$ is a composite function of two functions, $u$ and $v$.
Put $t=u(x)=a x+b$
$\frac{d v}{d t}=\frac{d}{d t}(\sin t)=\cos t=\cos (a x+b)$
$\frac{d t}{d x}=\frac{d}{d x}(a x+b)=\frac{d}{d x}(a x)+\frac{d}{d x}(b)=a+0=a$
Therefore, by chain rule, we obtain
$g^{\prime}=\frac{d g}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=\cos (a x+b) \cdot a=a \cos (a x+b)$
Consider $h(x)=\cos (c x+d)$
Let $p(x)=c x+d, q(y)=\cos y$
Then, $(q o p)(x)=q(p(x))=q(c x+d)=\cos (c x+d)=h(x)$
$\therefore h$ is a composite function of two functions, $p$ and $q$.
Put $y=p(x)=c x+d$
$\frac{d q}{d y}=\frac{d}{d y}(\cos y)=-\sin y=-\sin (c x+d)$
$\frac{d y}{d x}=\frac{d}{d x}(c x+d)=\frac{d}{d x}(c x)+\frac{d}{d x}(d)=c$
Therefore, by chain rule, we obtain
$h^{\prime}=\frac{d h}{d x}=\frac{d q}{d y} \cdot \frac{d y}{d x}=-\sin (c x+d) \times c=-c \sin (c x+d)$
$ \begin{aligned} \therefore f^{\prime} & =\frac{a \cos (a x+b) \cdot \cos (c x+d)-\sin (a x+b){-c \sin (c x+d)}}{[\cos (c x+d)]^{2}} \\ & =\frac{a \cos (a x+b)}{\cos (c x+d)}+c \sin (a x+b) \cdot \frac{\sin (c x+d)}{\cos (c x+d)} \times \frac{1}{\cos (c x+d)} \\ & =a \cos (a x+b) \sec (c x+d)+c \sin (a x+b) \tan (c x+d) \sec (c x+d) \end{aligned} $
6. $\cos x^{3} \cdot \sin ^{2}(x^{5})$
Show Answer
Solution
The given function is $\cos x^{3} \cdot \sin ^{2}(x^{5})$
$ \begin{aligned} & \frac{d}{d x}[\cos x^{3} \cdot \sin ^{2}(x^{5})]=\sin ^{2}(x^{5}) \times \frac{d}{d x}(\cos x^{3})+\cos x^{3} \times \frac{d}{d x}[\sin ^{2}(x^{5})] \\ & =\sin ^{2}(x^{5}) \times(-\sin x^{3}) \times \frac{d}{d x}(x^{3})+\cos x^{3} \times 2 \sin (x^{5}) \cdot \frac{d}{d x}[\sin x^{5}] \\ & =-\sin x^{3} \sin ^{2}(x^{5}) \times 3 x^{2}+2 \sin x^{5} \cos x^{3} \cdot \cos x^{5} \times \frac{d}{d x}(x^{5}) \\ & =-3 x^{2} \sin x^{3} \cdot \sin ^{2}(x^{5})+2 \sin x^{5} \cos x^{5} \cos x^{3} \cdot \times 5 x^{4} \\ & =10 x^{4} \sin x^{5} \cos x^{5} \cos x^{3}-3 x^{2} \sin x^{3} \sin ^{2}(x^{5}) \end{aligned} $
7. $2 \sqrt{\cot (x^{2})}$
Show Answer
Solution
$ \begin{aligned} & \frac{d}{d x}[2 \sqrt{\cot (x^{2})}] \\ & =2 \cdot \frac{1}{2 \sqrt{\cot (x^{2})}} \times \frac{d}{d x}[\cot (x^{2})] \\ & =\sqrt{\frac{\sin (x^{2})}{\cos (x^{2})}} \times-cosec^{2}(x^{2}) \times \frac{d}{d x}(x^{2}) \\ & =-\sqrt{\frac{\sin (x^{2})}{\cos (x^{2})}} \times \frac{1}{\sin ^{2}(x^{2})} \times(2 x) \\ & =\frac{-2 x}{\sqrt{\cos x^{2}} \sqrt{\sin x^{2}} \sin x^{2}} \\ & =\frac{-2 \sqrt{2} x}{\sqrt{2 \sin x^{2} \cos x^{2}} \sin x^{2}} \\ & =\frac{-2 \sqrt{2} x}{\sin x^{2} \sqrt{\sin 2 x^{2}}} \end{aligned} $
8. $\cos (\sqrt{x})$
Show Answer
Solution
Let $f(x)=\cos (\sqrt{x})$
Also, let $u(x)=\sqrt{x}$
And, $v(t)=\cos t$
Then, $($ vou $)(x)=v(u(x))$
$ \begin{aligned} & =v(\sqrt{x}) \\ & =\cos \sqrt{x} \\ & =f(x) \end{aligned} $
Clearly, $f$ is a composite function of two functions, $u$ and $v$, such that
$t=u(x)=\sqrt{x}$
Then, $\frac{d t}{d x}=\frac{d}{d x}(\sqrt{x})=\frac{d}{d x}(x^{\frac{1}{2}})=\frac{1}{2} x^{-\frac{1}{2}}$
$ =\frac{1}{2 \sqrt{x}} $
And, $\frac{d v}{d t}=\frac{d}{d t}(\cos t)=-\sin t$
$ =-\sin (\sqrt{x}) $
By using chain rule, we obtain
$ \begin{aligned} & \frac{d t}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x} \\ & =-\sin (\sqrt{x}) \cdot \frac{1}{2 \sqrt{x}} \\ & =-\frac{1}{2 \sqrt{x}} \sin (\sqrt{x}) \\ & =-\frac{\sin (\sqrt{x})}{2 \sqrt{x}} \end{aligned} $
Alternate method
$ \begin{aligned} \frac{d}{d x}[\cos (\sqrt{x})] & =-\sin (\sqrt{x}) \cdot \frac{d}{d x}(\sqrt{x}) \\ & =-\sin (\sqrt{x}) \times \frac{d}{d x}(x^{\frac{1}{2}}) \\ & =-\sin \sqrt{x} \times \frac{1}{2} x^{-\frac{1}{2}} \\ & =\frac{-\sin \sqrt{x}}{2 \sqrt{x}} \end{aligned} $
9. Prove that the function $f$ given by
$ f(x)=|x-1|, x \in \mathbf{R} $
is not differentiable at $x=1$.
Show Answer
Solution
The given function is $f(x)=|x-1|, x \in \mathbf{R}$
It is known that a function $f$ is differentiable at a point $x=c$ in its domain if both
$\lim _{h \to 0^{-}} \frac{f(c+h)-f(c)}{h}$ and $\lim _{h \to 0^{+}} \frac{f(c+h)-f(c)}{h}$ are finite and equal.
To check the differentiability of the given function at $x=1$,
consider the left hand limit of $f$ at $x=1$
$ \begin{aligned} & \lim _{h \to 0^{-}} \frac{f(1+h)-f(1)}{h}=\lim _{h \to 0^{-}} \frac{|1+h-1|-|1-1|}{h} \\ & \begin{aligned} =\lim _{h \to 0^{-}} \frac{|h|-0}{h} & =\lim _{h \to 0^{-}} \frac{-h}{h} \quad(h<0 \Rightarrow|h|=-h) \\ & =-1 \end{aligned} \end{aligned} $
Consider the right hand limit of $f$ at $x=1$
$ \begin{aligned} & \lim _{h \to 0^{+}} \frac{f(1+h)-f(1)}{h}=\lim _{h \to 0^{+}} \frac{|1+h-1|-|1-1|}{h} \\ & \begin{aligned} \lim _{h \to 0^{+}} \frac{|h|-0}{h} & =\lim _{h \to 0^{+}} \frac{h}{h} \quad(h>0 \Rightarrow|h|=h) \\ & =1 \end{aligned} \end{aligned} $
Since the left and right hand limits of $f$ at $x=1$ are not equal, $f$ is not differentiable at $x$ $=1$
10. Prove that the greatest integer function defined by
$ f(x)=[x], 0<x<3 $
is not differentiable at $x=1$ and $x=2$.
Show Answer
Solution
The given function $f$ is $f(x)=[x], 0<x<3$
It is known that a function $f$ is differentiable at a point $x=c$ in its domain if both
$\lim _{h \to 0^{-}} \frac{f(c+h)-f(c)}{h}$ and $\lim _{h \to 0^{+}} \frac{f(c+h)-f(c)}{h}$ are finite and equal.
To check the differentiability of the given function at $x=1$, consider the left hand limit of $f$ at $x=1$
$ \begin{aligned} & \lim _{h \to 0^{-}} \frac{f(1+h)-f(1)}{h}=\lim _{h \to 0^{-}} \frac{[1+h]-[1]}{h} \\ & =\lim _{h \to 0^{-}} \frac{0-1}{h}=\lim _{h \to 0^{-}} \frac{-1}{h}=\infty \end{aligned} $
Consider the right hand limit of $f$ at $x=1$
$\lim _{h \to 0^{+}} \frac{f(1+h)-f(1)}{h}=\lim _{h \to 0^{+}} \frac{[1+h]-[1]}{h}$
$=\lim _{h \to 0^{+}} \frac{1-1}{h}=\lim _{h \to 0^{+}} 0=0$
Since the left and right hand limits of $f$ at $x=1$ are not equal, $f$ is not differentiable at $x=1$
To check the differentiability of the given function at $x=2$, consider the left hand limit of $f$ at $x=2$
$\lim _{h \to 0^{-}} \frac{f(2+h)-f(2)}{h}=\lim _{h \to 0^{-}} \frac{[2+h]-[2]}{h}$
$=\lim _{h \to 0^{-}} \frac{1-2}{h}=\lim _{h \to 0^{-}} \frac{-1}{h}=\infty$
Consider the right hand limit of $f$ at $x=1$
$\lim _{h \to 0^{+}} \frac{f(2+h)-f(2)}{h}=\lim _{h \to 0^{+}} \frac{[2+h]-[2]}{h}$
$=\lim _{h \to 0^{+}} \frac{2-2}{h}=\lim _{h \to 0^{+}} 0=0$
Since the left and right hand limits of $f$ at $x=2$ are not equal, $f$ is not differentiable at $x$ $=2$
5.3.2 Derivatives of implicit functions
Until now we have been differentiating various functions given in the form $y=f(x)$. But it is not necessary that functions are always expressed in this form. For example, consider one of the following relationships between $x$ and $y$ :
$$ \begin{aligned} x-y-\pi & =0 \\ x+\sin x y-y & =0 \end{aligned} $$
In the first case, we can solve for $y$ and rewrite the relationship as $y=x-\pi$. In the second case, it does not seem that there is an easy way to solve for $y$. Nevertheless, there is no doubt about the dependence of $y$ on $x$ in either of the cases. When a relationship between $x$ and $y$ is expressed in a way that it is easy to solve for $y$ and write $y=f(x)$, we say that $y$ is given as an explicit function of $x$. In the latter case it is implicit that $y$ is a function of $x$ and we say that the relationship of the second type, above, gives function implicitly. In this subsection, we learn to differentiate implicit functions.
Example 22 Find $\frac{d y}{d x}$ if $x-y=\pi$.
Solution One way is to solve for $y$ and rewrite the above as
$$ \begin{aligned} y & =x-\pi \\ \end{aligned} $$
But then $\qquad\begin{aligned}\frac{d y}{d x} & =1\end{aligned}$
Alternatively, directly differentiating the relationship w.r.t., $x$, we have
$$ \frac{d}{d x}(x-y)=\frac{d \pi}{d x} $$
Recall that $\frac{d \pi}{d x}$ means to differentiate the constant function taking value $\pi$ everywhere w.r.t., $x$. Thus
$$ \frac{d}{d x}(x)-\frac{d}{d x}(y)=0 $$
which implies that $$ \frac{d y}{d x}=\frac{d x}{d x}=1 $$
Example 23 Find $\frac{d y}{d x}$, if $y+\sin y=\cos x$.
Solution We differentiate the relationship directly with respect to $x$, i.e.,
which implies using chain rule $ \frac{d y}{d x}+\frac{d}{d x}(\sin y)=\frac{d}{d x}(\cos x)$
This gives $\qquad \frac{d y}{d x}+\cos y \cdot \frac{d y}{d x}=-\sin x$
where $\qquad \begin{array}{r}\frac{d y}{d x}=-\frac{\sin x}{1+\cos y} \\y \neq(2 n+1) \pi\end{array}$
5.3.3 Derivatives of inverse trigonometric functions
We remark that inverse trigonometric functions are continuous functions, but we will not prove this. Now we use chain rule to find derivatives of these functions.
Example 24 Find the derivative of $f$ given by $f(x)=\sin ^{-1} x$ assuming it exists.
Solution Let $y=\sin ^{-1} x$. Then, $x=\sin y$.
Differentiating both sides w.r.t. $x$, we get
$$ \begin{aligned} & 1=\cos y \frac{d y}{d x} \\ \text{which implies that} \qquad \Rightarrow \quad & \frac{d y}{d x}=\frac{1}{\cos y}=\frac{1}{\cos \left(\sin ^{-1} x\right)} \end{aligned} $$
Observe that this is defined only for $\cos y \neq 0$, i.e.,
$\sin ^{-1} x \neq-\frac{\pi}{2}, \frac{\pi}{2}$, i.e., $x \neq-1,1$, i.e., $x \in(-1,1)$.
To make this result a bit more attractive, we carry out the following manipulation. Recall that for $x \in(-1,1), \sin (\sin ^{-1} x)=x$ and hence $ \cos ^{2} y=1-(\sin y)^{2}=1-(\sin (\sin ^{-1} x))^{2}=1-x^{2} $
Also, since $y \in(-\frac{\pi}{2}, \frac{\pi}{2}), \cos y$ is positive and hence $\cos y=\sqrt{1-x^{2}}$
Thus, for $x \in(-1,1)$, $\frac{d y}{d x}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-x^{2}}}$
| $f(x)$ | $\sin ^{-1} x$ | $\cos ^{-1} x$ | $\tan ^{-1} x$ |
|---|---|---|---|
| $f^{\prime}(x)$ | $\frac{1}{\sqrt{1-x^{2}}}$ | $\frac{-1}{\sqrt{1-x^{2}}}$ | $\frac{1}{1+x^{2}}$ |
| Domain of $f^{\prime}$ | $(-1,1)$ | $(-1,1)$ | $\mathbf{R}$ |
EXERCISE 5.3
Find $\frac{d y}{d x}$ in the following:
1. $2 x+3 y=\sin x$
Show Answer
Solution
The given relationship is $2 x+3 y=\sin x$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(2 x+3 y)=\frac{d}{d x}(\sin x)$
$\Rightarrow \frac{d}{d x}(2 x)+\frac{d}{d x}(3 y)=\cos x$
$\Rightarrow 2+3 \frac{d y}{d x}=\cos x$
$\Rightarrow 3 \frac{d y}{d x}=\cos x-2$
$\therefore \frac{d y}{d x}=\frac{\cos x-2}{3}$
2. $2 x+3 y=\sin y$
Show Answer
Solution
The given relationship is $2 x+3 y=\sin y$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(2 x)+\frac{d}{d x}(3 y)=\frac{d}{d x}(\sin y)$ $\Rightarrow 2+3 \frac{d y}{d x}=\cos y \frac{d y}{d x} \quad$ [By using chain rule]
$\Rightarrow 2=(\cos y-3) \frac{d y}{d x}$
$\therefore \frac{d y}{d x}=\frac{2}{\cos y-3}$
3. $a x+b y^{2}=\cos y$
Show Answer
Solution
The given relationship is $a x+b y^{2}=\cos y$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(a x)+\frac{d}{d x}(b y^{2})=\frac{d}{d x}(\cos y)$
$\Rightarrow a+b \frac{d}{d x}(y^{2})=\frac{d}{d x}(\cos y)$
Using chain rule, we obtain $\frac{d}{d x}(y^{2})=2 y \frac{d y}{d x}$ and $\frac{d}{d x}(\cos y)=-\sin y \frac{d y}{d x}$
From (1) and (2), we obtain
$a+b \times 2 y \frac{d y}{d x}=-\sin y \frac{d y}{d x}$
$\Rightarrow(2 b y+\sin y) \frac{d y}{d x}=-a$
$\therefore \frac{d y}{d x}=\frac{-a}{2 b y+\sin y}$
4. $x y+y^{2}=\tan x+y$
Show Answer
Solution
The given relationship is $x y+y^{2}=\tan x+y$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(x y+y^{2})=\frac{d}{d x}(\tan x+y)$
$\Rightarrow \frac{d}{d x}(x y)+\frac{d}{d x}(y^{2})=\frac{d}{d x}(\tan x)+\frac{d y}{d x}$
$\Rightarrow[y \cdot \frac{d}{d x}(x)+x \cdot \frac{d y}{d x}]+2 y \frac{d y}{d x}=\sec ^{2} x+\frac{d y}{d x} \quad$ [Using product rule and chain rule]
$\Rightarrow y \cdot 1+x \cdot \frac{d y}{d x}+2 y \frac{d y}{d x}=\sec ^{2} x+\frac{d y}{d x}$
$\Rightarrow(x+2 y-1) \frac{d y}{d x}=\sec ^{2} x-y$
$\therefore \frac{d y}{d x}=\frac{\sec ^{2} x-y}{(x+2 y-1)}$
5. $x^{2}+x y+y^{2}=100$
Show Answer
Solution
The given relationship is $x^{2}+x y+y^{2}=100$
Differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & \frac{d}{d x}(x^{2}+x y+y^{2})=\frac{d}{d x}(100) \\ & \Rightarrow \frac{d}{d x}(x^{2})+\frac{d}{d x}(x y)+\frac{d}{d x}(y^{2})=0 \end{aligned} $
$\Rightarrow 2 x+[y \cdot \frac{d}{d x}(x)+x \cdot \frac{d y}{d x}]+2 y \frac{d y}{d x}=0 \quad$ [Using product rule and chain rule]
$\Rightarrow 2 x+y \cdot 1+x \cdot \frac{d y}{d x}+2 y \frac{d y}{d x}=0$
$\Rightarrow 2 x+y+(x+2 y) \frac{d y}{d x}=0$
$\therefore \frac{d y}{d x}=-\frac{2 x+y}{x+2 y}$
6. $x^{3}+x^{2} y+x y^{2}+y^{3}=81$
Show Answer
Solution
The given relationship is $x^{3}+x^{2} y+x y^{2}+y^{3}=81$
Differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & \frac{d}{d x}(x^{3}+x^{2} y+x y^{2}+y^{3})=\frac{d}{d x}(81) \\ & \Rightarrow \frac{d}{d x}(x^{3})+\frac{d}{d x}(x^{2} y)+\frac{d}{d x}(x y^{2})+\frac{d}{d x}(y^{3})=0 \\ & \Rightarrow 3 x^{2}+[y \frac{d}{d x}(x^{2})+x^{2} \frac{d y}{d x}]+[y^{2} \frac{d}{d x}(x)+x \frac{d}{d x}(y^{2})]+3 y^{2} \frac{d y}{d x}=0 \\ & \Rightarrow 3 x^{2}+[y \cdot 2 x+x^{2} \frac{d y}{d x}]+[y^{2} \cdot 1+x \cdot 2 y \cdot \frac{d y}{d x}]+3 y^{2} \frac{d y}{d x}=0 \\ & \Rightarrow(x^{2}+2 x y+3 y^{2}) \frac{d y}{d x}+(3 x^{2}+2 x y+y^{2})=0 \\ & \therefore \frac{d y}{d x}=\frac{-(3 x^{2}+2 x y+y^{2})}{(x^{2}+2 x y+3 y^{2})} \end{aligned} $
7. $\sin ^{2} y+\cos x y=\kappa$
Show Answer
Solution
The given relationship is $\sin ^{2} y+\cos x y=\pi$
Differentiating this relationship with respect to $x$, we obtain
$$ \begin{align*} & \frac{d}{d x}(\sin ^{2} y+\cos x y)=\frac{d}{d x}(\pi) \\ & \Rightarrow \frac{d}{d x}(\sin ^{2} y)+\frac{d}{d x}(\cos x y)=0 \tag{1} \end{align*} $$
Using chain rule, we obtain
$$ \begin{align*} \frac{d}{d x}(\sin ^{2} y) & =2 \sin y \frac{d}{d x}(\sin y)=2 \sin y \cos y \frac{d y}{d x} \tag{2}\\ \frac{d}{d x}(\cos x y) & =-\sin x y \frac{d}{d x}(x y)=-\sin x y[y \frac{d}{d x}(x)+x \frac{d y}{d x}] \\ & =-\sin x y[y \cdot 1+x \frac{d y}{d x}]=-y \sin x y-x \sin x y \frac{d y}{d x} \tag{3} \end{align*} $$
From (1), (2), and (3), we obtain
$2 \sin y \cos y \frac{d y}{d x}-y \sin x y-x \sin x y \frac{d y}{d x}=0$
$\Rightarrow(2 \sin y \cos y-x \sin x y) \frac{d y}{d x}=y \sin x y$
$\Rightarrow(\sin 2 y-x \sin x y) \frac{d y}{d x}=y \sin x y$
$\therefore \frac{d y}{d x}=\frac{y \sin x y}{\sin 2 y-x \sin x y}$
8. $\sin ^{2} x+\cos ^{2} y=1$
Show Answer
Solution
The given relationship is $\sin ^{2} x+\cos ^{2} y=1$
Differentiating this relationship with respect to $x$, we obtain $\frac{d}{d x}(\sin ^{2} x+\cos ^{2} y)=\frac{d}{d x}(1)$
$\Rightarrow \frac{d}{d x}(\sin ^{2} x)+\frac{d}{d x}(\cos ^{2} y)=0$
$\Rightarrow 2 \sin x \cdot \frac{d}{d x}(\sin x)+2 \cos y \cdot \frac{d}{d x}(\cos y)=0$
$\Rightarrow 2 \sin x \cos x+2 \cos y(-\sin y) \cdot \frac{d y}{d x}=0$
$\Rightarrow \sin 2 x-\sin 2 y \frac{d y}{d x}=0$
$\therefore \frac{d y}{d x}=\frac{\sin 2 x}{\sin 2 y}$
9. $y=\sin ^{-1}(\frac{2 x}{1+x^{2}})$
Show Answer
Solution
The given relationship is $y=\sin ^{-1}(\frac{2 x}{1+x^{2}})$
$y=\sin ^{-1}(\frac{2 x}{1+x^{2}})$
$\Rightarrow \sin y=\frac{2 x}{1+x^{2}}$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(\sin y)=\frac{d}{d x}(\frac{2 x}{1+x^{2}})$
$\Rightarrow \cos y \frac{d y}{d x}=\frac{d}{d x}(\frac{2 x}{1+x^{2}})$
The function, $\frac{2 x}{1+x^{2}}$, is of the form of $\frac{u}{v}$.
Therefore, by quotient rule, we obtain
$$ \begin{align*} & \frac{d}{d x}(\frac{2 x}{1+x^{2}})=\frac{(1+x^{2}) \cdot \frac{d}{d x}(2 x)-2 x \cdot \frac{d}{d x}(1+x^{2})}{(1+x^{2})^{2}} \\ & =\frac{(1+x^{2}) \cdot 2-2 x \cdot[0+2 x]}{(1+x^{2})^{2}}=\frac{2+2 x^{2}-4 x^{2}}{(1+x^{2})^{2}}=\frac{2(1-x^{2})}{(1+x^{2})^{2}} \tag{2} \end{align*} $$
Also, $\sin y=\frac{2 x}{1+x^{2}}$
$$ \begin{align*} \Rightarrow \cos y & =\sqrt{1-\sin ^{2} y}=\sqrt{1-(\frac{2 x}{1+x^{2}})^{2}}=\sqrt{\frac{(1+x^{2})^{2}-4 x^{2}}{(1+x^{2})^{2}}} \\ & =\sqrt{\frac{(1-x^{2})^{2}}{(1+x^{2})^{2}}}=\frac{1-x^{2}}{1+x^{2}} \tag{3} \end{align*} $$
From (1), (2), and (3), we obtain
$ \begin{aligned} & \frac{1-x^{2}}{1+x^{2}} \times \frac{d y}{d x}=\frac{2(1-x^{2})}{(1+x^{2})^{2}} \\ & \Rightarrow \frac{d y}{d x}=\frac{2}{1+x^{2}} \end{aligned} $
10. $y=\tan ^{-1}(\frac{3 x-x^{3}}{1-3 x^{2}}),-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}$
Show Answer
Solution
The given relationship is $y=\tan ^{-1}(\frac{3 x-x^{3}}{1-3 x^{2}})$ $y=\tan ^{-1}(\frac{3 x-x^{3}}{1-3 x^{2}})$
$\Rightarrow \tan y=\frac{3 x-x^{3}}{1-3 x^{2}}$
It is known that, $\tan y=\frac{3 \tan \frac{y}{3}-\tan ^{3} \frac{y}{3}}{1-3 \tan ^{2} \frac{y}{3}}$
Comparing equations (1) and (2), we obtain
$x=\tan \frac{y}{3}$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(x)=\frac{d}{d x}(\tan \frac{y}{3})$
$\Rightarrow 1=\sec ^{2} \frac{y}{3} \cdot \frac{d}{d x}(\frac{y}{3})$
$\Rightarrow 1=\sec ^{2} \frac{y}{3} \cdot \frac{1}{3} \cdot \frac{d y}{d x}$
$\Rightarrow \frac{d y}{d x}=\frac{3}{\sec ^{2} \frac{y}{3}}=\frac{3}{1+\tan ^{2} \frac{y}{3}}$
$\therefore \frac{d y}{d x}=\frac{3}{1+x^{2}}$
11. $y=\cos ^{-1}(\frac{1-x^{2}}{1+x^{2}}), 0<x<1$
Show Answer
Solution
The given relationship is, $y=\cos ^{-1}(\frac{1-x^{2}}{1+x^{2}})$
$\Rightarrow \cos y=\frac{1-x^{2}}{1+x^{2}}$
$\Rightarrow \frac{1-\tan ^{2} \frac{y}{2}}{1+\tan ^{2} \frac{y}{2}}=\frac{1-x^{2}}{1+x^{2}}$
On comparing L.H.S. and R.H.S. of the above relationship, we obtain
$\tan \frac{y}{2}=x$
Differentiating this relationship with respect to $x$, we obtain
$\sec ^{2} \frac{y}{2} \cdot \frac{d}{d x}(\frac{y}{2})=\frac{d}{d x}(x)$
$\Rightarrow \sec ^{2} \frac{y}{2} \times \frac{1}{2} \frac{d y}{d x}=1$
$\Rightarrow \frac{d y}{d x}=\frac{2}{\sec ^{2} \frac{y}{2}}$
$\Rightarrow \frac{d y}{d x}=\frac{2}{1+\tan ^{2} \frac{y}{2}}$
$\therefore \frac{d y}{d x}=\frac{1}{1+x^{2}}$
12. $y=\sin ^{-1}(\frac{1-x^{2}}{1+x^{2}}), 0<x<1$
Show Answer
Solution
The given relationship is $y=\sin ^{-1}(\frac{1-x^{2}}{1+x^{2}})$ $y=\sin ^{-1}(\frac{1-x^{2}}{1+x^{2}})$
$\Rightarrow \sin y=\frac{1-x^{2}}{1+x^{2}}$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(\sin y)=\frac{d}{d x}(\frac{1-x^{2}}{1+x^{2}})$
Using chain rule, we obtain
$ \frac{d}{d x}(\sin y)=\cos y \cdot \frac{d y}{d x} $
$ \begin{aligned} & \cos y=\sqrt{1-\sin ^{2} y}=\sqrt{1-(\frac{1-x^{2}}{1+x^{2}})^{2}} \\ & =\sqrt{\frac{(1+x^{2})^{2}-(1-x^{2})^{2}}{(1+x^{2})^{2}}}=\sqrt{\frac{4 x^{2}}{(1+x^{2})^{2}}}=\frac{2 x}{1+x^{2}} \\ & \therefore \frac{d}{d x}(\sin y)=\frac{2 x}{1+x^{2}} \frac{d y}{d x} \end{aligned} $
$\frac{d}{d x}(\frac{1-x^{2}}{1+x^{2}})=\frac{(1+x^{2}) \cdot(1-x^{2})^{\prime}-(1-x^{2}) \cdot(1+x^{2})^{\prime}}{(1+x^{2})^{2}}$
[Using quotient rule]
$=\frac{(1+x^{2})(-2 x)-(1-x^{2}) \cdot(2 x)}{(1+x^{2})^{2}}$
$=\frac{-2 x-2 x^{3}-2 x+2 x^{3}}{(1+x^{2})^{2}}$
$=\frac{-4 x}{(1+x^{2})^{2}}$
From (1), (2), and (3), we obtain
$ \begin{aligned} & \frac{2 x}{1+x^{2}} \frac{d y}{d x}=\frac{-4 x}{(1+x^{2})^{2}} \\ & \Rightarrow \frac{d y}{d x}=\frac{-2}{1+x^{2}} \end{aligned} $
Alternate method
$ \begin{aligned} & y=\sin ^{-1}(\frac{1-x^{2}}{1+x^{2}}) \\ & \Rightarrow \sin y=\frac{1-x^{2}}{1+x^{2}} \end{aligned} $
$\Rightarrow(1+x^{2}) \sin y=1-x^{2}$
$\Rightarrow(1+\sin y) x^{2}=1-\sin y$
$\Rightarrow x^{2}=\frac{1-\sin y}{1+\sin y}$
$\Rightarrow x^{2}=\frac{(\cos \frac{y}{2}-\sin \frac{y}{2})^{2}}{(\cos \frac{y}{2}+\sin \frac{y}{2})^{2}}$
$\Rightarrow x=\frac{\cos \frac{y}{2}-\sin \frac{y}{2}}{\cos \frac{y}{2}+\sin \frac{y}{2}}$
$\Rightarrow x=\frac{1-\tan \frac{y}{2}}{1+\tan \frac{y}{2}}$
$\Rightarrow x=\tan (\frac{\pi}{4}-\frac{y}{2})$
Differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & \frac{d}{d x}(x)=\frac{d}{d x} \cdot[\tan (\frac{\pi}{4}-\frac{y}{2})] \\ & \Rightarrow 1=\sec ^{2}(\frac{\pi}{4}-\frac{y}{2}) \cdot \frac{d}{d x}(\frac{\pi}{4}-\frac{y}{2}) \\ & \Rightarrow 1=[1+\tan ^{2}(\frac{\pi}{4}-\frac{y}{2})] \cdot(-\frac{1}{2} \frac{d y}{d x}) \\ & \Rightarrow 1=(1+x^{2})(-\frac{1}{2} \frac{d y}{d x}) \\ & \Rightarrow \frac{d y}{d x}=\frac{-2}{1+x^{2}} \end{aligned} $
13. $y=\cos ^{-1}(\frac{2 x}{1+x^{2}}),-1<x<1$
Show Answer
Solution
The given relationship is $y=\cos ^{-1}(\frac{2 x}{1+x^{2}})$
$ \begin{aligned} & y=\cos ^{-1}(\frac{2 x}{1+x^{2}}) \\ & \Rightarrow \cos y=\frac{2 x}{1+x^{2}} \end{aligned} $
Differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & \frac{d}{d x}(\cos y)=\frac{d}{d x} \cdot(\frac{2 x}{1+x^{2}}) \\ & \Rightarrow-\sin y \cdot \frac{d y}{d x}=\frac{(1+x^{2}) \cdot \frac{d}{d x}(2 x)-2 x \cdot \frac{d}{d x}(1+x^{2})}{(1+x^{2})^{2}} \end{aligned} $
$ \begin{aligned} & \Rightarrow-\sqrt{1-\cos ^{2} y} \frac{d y}{d x}=\frac{(1+x^{2}) \times 2-2 x \cdot 2 x}{(1+x^{2})^{2}} \\ & \Rightarrow[\sqrt{1-(\frac{2 x}{1+x^{2}})^{2}}] \frac{d y}{d x}=-[\frac{2(1-x^{2})}{(1+x^{2})^{2}}] \\ & \Rightarrow \sqrt{\frac{(1+x^{2})^{2}-4 x^{2}}{(1+x^{2})^{2}}} \frac{d y}{d x}=\frac{-2(1-x^{2})}{(1+x^{2})^{2}} \\ & \Rightarrow \sqrt{\frac{(1-x^{2})^{2}}{(1+x^{2})^{2}}} \frac{d y}{d x}=\frac{-2(1-x^{2})}{(1+x^{2})^{2}} \\ & \Rightarrow \frac{1-x^{2}}{1+x^{2}} \cdot \frac{d y}{d x}=\frac{-2(1-x^{2})}{(1+x^{2})^{2}} \\ & \Rightarrow \frac{d y}{d x}=\frac{-2}{1+x^{2}} \end{aligned} $
14. $y=\sin ^{-1}(2 x \sqrt{1-x^{2}}),-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}$
Show Answer
Solution
The given relationship is $y=\sin ^{-1}(2 x \sqrt{1-x^{2}})$
$y=\sin ^{-1}(2 x \sqrt{1-x^{2}})$
$\Rightarrow \sin y=2 x \sqrt{1-x^{2}}$
Differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & \cos y \frac{d y}{d x}=2[x \frac{d}{d x}(\sqrt{1-x^{2}})+\sqrt{1-x^{2}} \frac{d x}{d x}] \\ & \Rightarrow \sqrt{1-\sin ^{2} y} \frac{d y}{d x}=2[\frac{x}{2} \cdot \frac{-2 x}{\sqrt{1-x^{2}}}+\sqrt{1-x^{2}}] \\ & \Rightarrow \sqrt{1-(2 x \sqrt{1-x^{2}})^{2}} \frac{d y}{d x}=2[\frac{-x^{2}+1-x^{2}}{\sqrt{1-x^{2}}}] \\ & \Rightarrow \sqrt{1-4 x^{2}(1-x^{2})} \frac{d y}{d x}=2[\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}] \\ & \Rightarrow \sqrt{(1-2 x^{2})^{2}} \frac{d y}{d x}=2[\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}] \\ & \Rightarrow(1-2 x^{2}) \frac{d y}{d x}=2[\frac{1-2 x^{2}}{\sqrt{1-x^{2}}}] \\ & \Rightarrow \frac{d y}{d x}=\frac{2}{\sqrt{1-x^{2}}} \end{aligned} $
15. $y=\sec ^{-1}(\frac{1}{2 x^{2}-1}), 0<x<\frac{1}{\sqrt{2}}$
Show Answer
Solution
The given relationship is $y=\sec ^{-1}(\frac{1}{2 x^{2}-1})$
$ y=\sec ^{-1}(\frac{1}{2 x^{2}-1}) $
$\Rightarrow \sec y=\frac{1}{2 x^{2}-1}$
$\Rightarrow \cos y=2 x^{2}-1$
$\Rightarrow 2 x^{2}=1+\cos y$
$\Rightarrow 2 x^{2}=2 \cos ^{2} \frac{y}{2}$
$\Rightarrow x=\cos \frac{y}{2}$
Differentiating this relationship with respect to $x$, we obtain
$\frac{d}{d x}(x)=\frac{d}{d x}(\cos \frac{y}{2})$
$\Rightarrow 1=-\sin \frac{y}{2} \cdot \frac{d}{d x}(\frac{y}{2})$
$\Rightarrow \frac{-1}{\sin \frac{y}{2}}=\frac{1}{2} \frac{d y}{d x}$
$\Rightarrow \frac{d y}{d x}=\frac{-2}{\sin \frac{y}{2}}=\frac{-2}{\sqrt{1-\cos ^{2} \frac{y}{2}}}$
$\Rightarrow \frac{d y}{d x}=\frac{-2}{\sqrt{1-x^{2}}}$
5.4 Exponential and Logarithmic Functions
Till now we have learnt some aspects of different classes of functions like polynomial functions, rational functions and trigonometric functions. In this section, we shall learn about a new class of (related) functions called exponential functions and logarithmic functions. It needs to be emphasized that many statements made in this section are motivational and precise proofs of these are well beyond the scope of this text.
The Fig 5.9 gives a sketch of $y=f_1(x)=x, y=f_2(x)=x^{2}, y=f_3(x)=x^{3}$ and $y=f_4(x)$ $=x^{4}$. Observe that the curves get steeper as the power of $x$ increases. Steeper the curve, faster is the rate of growth. What this means is that for a fixed increment in the value of $x(>1)$, the increment in the value of $y=f_n(x)$ increases as $n$ increases for $n$ $=1,2,3,4$. It is conceivable that such a statement is true for all positive values of $n$, where $f_n(x)=x^{n}$. Essentially, this means that the graph of $y=f_n(x)$ leans more towards the $y$-axis as $n$ increases. For example, consider $f _{10}(x)=x^{10}$ and $f _{15}(x)$ $=x^{15}$. If $x$ increases from 1 to $2, f _{10}$ increases from 1 to $2^{10}$ whereas $f _{15}$ increases from 1 to $2^{15}$. Thus, for the same increment in $x, f _{15}$ grow faster than $f _{10}$.
Upshot of the above discussion is that the growth of polynomial functions is dependent on the degree of the polynomial function - higher the degree, greater is the growth. The next natural question is:
Fig 5.9 Is there a function which grows faster than any polynomial function. The answer is in affirmative and an example of such a function is
$ y=f(x)=10^{x} . $ Our claim is that this function $f$ grows faster than $f_n(x)=x^{n}$ for any positive integer $n$. For example, we can prove that $10^{x}$ grows faster than $f _{100}(x)=x^{100}$. For large values of $x$ like $x=10^{3}$, note that $f _{100}(x)=(10^{3})^{100}=10^{300}$ whereas $f(10^{3})=10^{10^{3}}=10^{1000}$.
Clearly $f(x)$ is much greater than $f _{100}(x)$. It is not difficult to prove that for all $x>10^{3}, f(x)>f _{100}(x)$. But we will not attempt to give a proof of this here. Similarly, by choosing large values of $x$, one can verify that $f(x)$ grows faster than $f_n(x)$ for any positive integer $n$.
Definition 3 The exponential function with positive base $b>1$ is the function $y=f(x)=b^{x}$
The graph of $y=10^{x}$ is given in the Fig 5.9.
It is advised that the reader plots this graph for particular values of $b$ like 2,3 and 4. Following are some of the salient features of the exponential functions:
(1) Domain of the exponential function is $\mathbf{R}$, the set of all real numbers.
(2) Range of the exponential function is the set of all positive real numbers.
(3) The point $(0,1)$ is always on the graph of the exponential function (this is a restatement of the fact that $b^{0}=1$ for any real $b>1$ ).
(4) Exponential function is ever increasing; i.e., as we move from left to right, the graph rises above.
(5) For very large negative values of $x$, the exponential function is very close to 0 . In other words, in the second quadrant, the graph approaches $x$-axis (but never meets it).
Exponential function with base 10 is called the common exponential function. In the Appendix A.1.4 of Class XI, it was observed that the sum of the series
$$ 1+\frac{1}{1 !}+\frac{1}{2 !}+\ldots \text { } $$
is a number between 2 and 3 and is denoted by $e$. Using this $e$ as the base we obtain an extremely important exponential function $y=e^{x}$.
This is called natural exponential function. It would be interesting to know if the inverse of the exponential function exists and has nice interpretation. This search motivates the following definition.
Definition 4 Let $b>1$ be a real number. Then we say logarithm of $a$ to base $b$ is $x$ if $b^{x}=a$.
Logarithm of $a$ to base $b$ is denoted by $\log _{b} a$. Thus $\log _{b} a=x$ if $b^{x}=a$. Let us work with a few explicit examples to get a feel for this. We know $2^{3}=8$. In terms of logarithms, we may rewrite this as $\log _2 8=3$. Similarly, $10^{4}=10000$ is equivalent to saying $\log _{10} 10000=4$. Also, $625=5^{4}=25^{2}$ is equivalent to saying $\log _5 625=4$ or $\log _{25} 625=2$.
On a slightly more mature note, fixing a base $b>1$, we may look at logarithm as a function from positive real numbers to all real numbers. This function, called the logarithmic function, is defined by
$$ \begin{aligned} \log _{b}: \mathbf{R}^{+} & \to \mathbf{R} \\ x & \to \log _{b} x=y \text{ if } b^{y}=x \end{aligned} $$
As before if the base $b=10$, we say it is common logarithms and if $b=e$, then we say it is natural logarithms. Often natural logarithm is denoted by $\ln$. In this chapter, $\log x$ denotes the logarithm function to base e, i.e., $\ln x$ will be written as simply $\log x$. The Fig 5.10 gives the plots of logarithm function to base 2, $e$ and 10.
Some of the important observations about the logarithm function to any base $b>1$ are listed below:
Fig 5.10
(1) We cannot make a meaningful definition of logarithm of non-positive numbers and hence the domain of log function is $\mathbf{R}^{+}$.
(2) The range of log function is the set of all real numbers.
(3) The point $(1,0)$ is always on the graph of the log function.
(4) The log function is ever increasing, i.e., as we move from left to right the graph rises above.
(5) For $x$ very near to zero, the value of $\log x$ can be made lesser than any given real number. In other words in the fourth quadrant the graph approaches $y$-axis (but never meets it).
(6) Fig 5.11 gives the plot of $y=e^{x}$ and $y=\ln x$. It is of interest to observe that the two curves are the mirror

Fig 5.11 images of each other reflected in the line $y=x$.
Two properties of ’ $\log$ ’ functions are proved below:
(1) There is a standard change of base rule to obtain $\log _{a} p$ in terms of $\log _{b} p$. Let $\log _{a} p=\alpha, \log _{b} p=\beta$ and $\log _{b} a=\gamma$. This means $a^{\alpha}=p, b^{\beta}=p$ and $b^{\gamma}=a$.
Substituting the third equation in the first one, we have
$$ (b^{\gamma})^{\alpha}=b^{\gamma \alpha}=p $$
Using this in the second equation, we get
$$ \begin{aligned} b^{\beta} & =p=b^{\gamma \alpha} \\ \text{which implies }\beta & =\alpha \gamma \text { or } \alpha=\frac{\beta}{\gamma}. \text{ But then } \\ \log _{a} p & =\frac{\log _{b} p}{\log _{b} a} \end{aligned} $$
(2) Another interesting property of the log function is its effect on products. Let $\log _{b} p q=\alpha$. Then $b^{\alpha}=p q$. If $\log _{b} p=\beta$ and $\log _{b} q=\gamma$, then $b^{\beta}=p$ and $b^{\gamma}=q$. But then $b^{\alpha}=p q=b^{\beta} b^{\gamma}=b^{\beta+\gamma}$
which implies $\alpha=\beta+\gamma$, i.e.,
$$ \log _{b} p q=\log _{b} p+\log _{b} q $$
A particularly interesting and important consequence of this is when $p=q$. In this case the above may be rewritten as
$$ \log _{b} p^{2}=\log _{b} p+\log _{b} p=2 \log p $$
An easy generalisation of this (left as an exercise!) is
$$ \log _{b} p^{n}=n \log p $$
for any positive integer $n$. In fact this is true for any real number $n$, but we will not attempt to prove this. On the similar lines the reader is invited to verify
$$ \log _{b} \frac{x}{y}=\log _{b} x-\log _{b} y $$
Example 25 Is it true that $x=e^{\log x}$ for all real $x$ ?
Solution First, observe that the domain of log function is set of all positive real numbers. So the above equation is not true for non-positive real numbers. Now, let $y=e^{\log x}$. If $y>0$, we may take $\log$ arithm which gives us $\log y=\log (e^{\log x})=\log x \cdot \log e=\log x$. Thus $y=x$. Hence $x=e^{\log x}$ is true only for positive values of $x$.
One of the striking properties of the natural exponential function in differential calculus is that it doesn’t change during the process of differentiation. This is captured in the following theorem whose proof we skip.
Theorem 5
(1) The derivative of $e^{x}$ w.r.t., $x$ is $e^{x}$; i.e., $\frac{d}{d x}(e^{x})=e^{x}$.
(2) The derivative of $\log x$ w.r.t., $x$ is $\frac{1}{x}$; i.e., $\frac{d}{d x}(\log x)=\frac{1}{x}$.
Example 26 Differentiate the following w.r.t. $x$ :
(i) $e^{-x}$
(ii) $\sin (\log x), x>0$
(iii) $\cos ^{-1}(e^{x})$
(iv) $e^{\cos x}$
Solution
(i) Let $y=e^{-x}$. Using chain rule, we have
$$ \frac{d y}{d x}=e^{-x} \cdot \frac{d}{d x}(-x)=-e^{-x} $$
(ii) Let $y=\sin (\log x)$. Using chain rule, we have
$$ \frac{d y}{d x}=\cos (\log x) \cdot \frac{d}{d x}(\log x)=\frac{\cos (\log x)}{x} $$
(iii) Let $y=\cos ^{-1}(e^{x})$. Using chain rule, we have
$$ \frac{d y}{d x}=\frac{-1}{\sqrt{1-\left(e^{x}\right)^{2}}} \cdot \frac{d}{d x}\left(e^{x}\right)=\frac{-e^{x}}{\sqrt{1-e^{2 x}}} . $$
(iv) Let $y=e^{\cos x}$. Using chain rule, we have
$$ \frac{d y}{d x}=e^{\cos x} \cdot(-\sin x)=-(\sin x) e^{\cos x} $$[^0]
EXERCISE 5.4
Differentiate the following w.r.t. $x$ :
1. $\frac{e^{x}}{\sin x}$
Show Answer
Solution
Let $y=\frac{e^{x}}{\sin x}$
By using the quotient rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{\sin x \frac{d}{d x}(e^{x})-e^{x} \frac{d}{d x}(\sin x)}{\sin ^{2} x} \\ & =\frac{\sin x \cdot(e^{x})-e^{x} \cdot(\cos x)}{\sin ^{2} x} \\ & =\frac{e^{x}(\sin x-\cos x)}{\sin ^{2} x}, x \neq n \pi, n \in \mathbf{Z} \end{aligned} $
2. $e^{\sin ^{-1} x}$
Show Answer
Solution
Let $y=e^{\sin ^{-1} x}$
By using the chain rule, we obtain
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(e^{\sin ^{-1} x}) \\ & \begin{aligned} \Rightarrow \frac{d y}{d x} & =e^{\sin ^{-1} x} \cdot \frac{d}{d x}(\sin ^{-1} x) \\ & =e^{\sin ^{-1} x} \cdot \frac{1}{\sqrt{1-x^{2}}} \\ & =\frac{e^{\sin ^{-1} x}}{\sqrt{1-x^{2}}} \end{aligned} \\ & \therefore \frac{d y}{d x}=\frac{e^{\sin ^{-1} x}}{\sqrt{1-x^{2}}}, x \in(-1,1) \end{aligned} $
3. $e^{x^{3}}$
Show Answer
Solution
Let $y=e^{x^{3}}$
By using the chain rule, we obtain
$\frac{d y}{d x}=\frac{d}{d x}(e^{x^{3}})=e^{x^{3}} \cdot \frac{d}{d x}(x^{3})=e^{x^{3}} \cdot 3 x^{2}=3 x^{2} e^{x^{3}}$
4. $\sin (\tan ^{-1} e^{-x})$
Show Answer
Solution
Let $y=\sin (\tan ^{-1} e^{-x})$
By using the chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}[\sin (\tan ^{-1} e^{-x})] \\ & =\cos (\tan ^{-1} e^{-x}) \cdot \frac{d}{d x}(\tan ^{-1} e^{-x}) \\ & =\cos (\tan ^{-1} e^{-x}) \cdot \frac{1}{1+(e^{-x})^{2}} \cdot \frac{d}{d x}(e^{-x}) \\ & =\frac{\cos (\tan ^{-1} e^{-x})}{1+e^{-2 x}} \cdot e^{-x} \cdot \frac{d}{d x}(-x) \\ & =\frac{e^{-x} \cos (\tan ^{-1} e^{-x})}{1+e^{-2 x}} \times(-1) \\ & =\frac{-e^{-x} \cos (\tan ^{-1} e^{-x})}{1+e^{-2 x}} \end{aligned} $
5. $\log (\cos e^{x})$
Show Answer
Solution
Let $y=\log (\cos e^{x})$
By using the chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}[\log (\cos e^{x})] \\ & =\frac{1}{\cos e^{x}} \cdot \frac{d}{d x}(\cos e^{x}) \\ & =\frac{1}{\cos e^{x}} \cdot(-\sin e^{x}) \cdot \frac{d}{d x}(e^{x}) \\ & =\frac{-\sin e^{x}}{\cos e^{x}} \cdot e^{x} \\ & =-e^{x} \tan e^{x}, e^{x} \neq(2 n+1) \frac{\pi}{2}, n \in \mathbf{N} \end{aligned} $
6. $e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}$
Show Answer
Solution
$\frac{d}{d x}(e^{x}+e^{x^{2}}+\ldots+e^{x^{3}})$
$=\frac{d}{d x}(e^{x})+\frac{d}{d x}(e^{x^{2}})+\frac{d}{d x}(e^{x^{3}})+\frac{d}{d x}(e^{x^{4}})+\frac{d}{d x}(e^{x^{3}})$
$=e^{x}+[e^{x^{2}} \times \frac{d}{d x}(x^{2})]+[e^{x^{3}} \cdot \frac{d}{d x}(x^{3})]+[e^{x^{4}} \cdot \frac{d}{d x}(x^{4})]+[e^{x^{5}} \cdot \frac{d}{d x}(x^{5})]$
$=e^{x}+(e^{x^{2}} \times 2 x)+(e^{x^{3}} \times 3 x^{2})+(e^{x^{4}} \times 4 x^{3})+(e^{x^{3}} \times 5 x^{4})$
$=e^{x}+2 x e^{x^{2}}+3 x^{2} e^{x^{3}}+4 x^{3} e^{x^{4}}+5 x^{4} e^{x^{5}}$
7. $\sqrt{e^{\sqrt{x}}}, x>0$
Show Answer
Solution
Let $y=\sqrt{e^{\sqrt{x}}}$
Then, $y^{2}=e^{\sqrt{x}}$
By differentiating this relationship with respect to $x$, we obtain
$ \begin{aligned} & y^{2}=e^{\sqrt{x}} \\ & \Rightarrow 2 y \frac{d y}{d x}=e^{\sqrt{x}} \frac{d}{d x}(\sqrt{x}) \quad \text{ [By applying the chain rule] } \\ & \Rightarrow 2 y \frac{d y}{d x}=e^{\sqrt{x}} \frac{1}{2} \cdot \frac{1}{\sqrt{x}} \\ & \Rightarrow \frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 y \sqrt{x}} \\ & \Rightarrow \frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{e^{\sqrt{x}}} \sqrt{x}} \\ & \Rightarrow \frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{x e^{\sqrt{x}}}}, x>0 \end{aligned} $
8. $\log (\log x), x>1$
Show Answer
Solution
Let $y=\log (\log x)$
By using the chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}[\log (\log x)] \\ & =\frac{1}{\log x} \cdot \frac{d}{d x}(\log x) \\ & =\frac{1}{\log x} \cdot \frac{1}{x} \\ = & \frac{1}{x \log x}, x>1 \end{aligned} $
9. $\frac{\cos x}{\log x}, x>0$
Show Answer
Solution
Let $y=\frac{\cos x}{\log x}$
By using the quotient rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{\frac{d}{d x}(\cos x) \times \log x-\cos x \times \frac{d}{d x}(\log x)}{(\log x)^{2}} \\ & =\frac{-\sin x \log x-\cos x \times \frac{1}{x}}{(\log x)^{2}} \\ & =\frac{-[x \log x \cdot \sin x+\cos x]}{x(\log x)^{2}}, x>0 \end{aligned} $
10. $\cos (\log x+e^{x}), x>0$
Show Answer
Solution
Let $y=\cos (\log x+e^{x})$
By using the chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =-\sin (\log x+e^{x}) \cdot \frac{d}{d x}(\log x+e^{x}) \\ & =-\sin (\log x+e^{x}) \cdot[\frac{d}{d x}(\log x)+\frac{d}{d x}(e^{x})] \\ & =-\sin (\log x+e^{x}) \cdot(\frac{1}{x}+e^{x}) \\ & =-(\frac{1}{x}+e^{x}) \sin (\log x+e^{x}), x>0 \end{aligned} $
5.5 Logarithmic Differentiation
In this section, we will learn to differentiate certain special class of functions given in the form
$$ y=f(x)=[u(x)]^{v(x)} $$
By taking logarithm (to base $e$ ) the above may be rewritten as
$$ \log y=v(x) \log [u(x)] $$
Using chain rule we may differentiate this to get
$$ \frac{1}{y} \cdot \frac{d y}{d x}=v(x) \cdot \frac{1}{u(x)} \cdot u^{\prime}(x)+v^{\prime}(x) \cdot \log [u(x)] $$
which implies that
$$ \frac{d y}{d x}=y[\frac{v(x)}{u(x)} \cdot u^{\prime}(x)+v^{\prime}(x) \cdot \log [u(x)]] $$
The main point to be noted in this method is that $f(x)$ and $u(x)$ must always be positive as otherwise their logarithms are not defined. This process of differentiation is known as logarithms differentiation and is illustrated by the following examples:
Example 26 Differentiate $\sqrt{\frac{(x-3)(x^{2}+4)}{3 x^{2}+4 x+5}}$ w.r.t. $x$.
Solution Let $y=\sqrt{\frac{(x-3)(x^{2}+4)}{(3 x^{2}+4 x+5)}}$
Taking logarithm on both sides, we have
$$ \log y=\frac{1}{2}[\log (x-3)+\log (x^{2}+4)-\log (3 x^{2}+4 x+5)] $$
Now, differentiating both sides w.r.t. $x$, we get
$$ \frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right] $$
or $\qquad\frac{d y}{d x}=\frac{y}{2}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right]$
$$ =\frac{1}{2} \sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right] $$
Example 27 Differentiate $a^{x}$ w.r.t. $x$, where $a$ is a positive constant.
Solution Let $y=a^{x}$. Then
$$ \log y=x \log a $$
Differentiating both sides w.r.t. $x$, we have
$ \begin{aligned} & \frac{1}{y} \frac{d y}{d x}=\log a \\ \text{ or } \qquad & \frac{d y}{d x}=y \log a \\ \text{ Thus } \qquad & \frac{d}{d x}\left(a^x\right)=a^x \log a \\ \text { Alternatively } \qquad & \frac{d}{d x}\left(a^x\right) =\frac{d}{d x}\left(e^{x \log a}\right)=e^{x \log a} \frac{d}{d x}(x \log a) \\ & =e^{x \log a} \cdot \log a=a^x \log a \end{aligned} $
Example 28 Differentiate $x^{\sin x}, x>0$ w.r.t. $x$.
Solution Let $y=x^{\sin x}$. Taking logarithm on both sides, we have
$$ \begin{aligned} \log y & =\sin x \log x \\ \frac{1}{y} \cdot \frac{d y}{d x} & =\sin x \frac{d}{d x}(\log x)+\log x \frac{d}{d x}(\sin x) \end{aligned} $$
Therefore $\qquad \frac{1}{y} \frac{d y}{d x}=(\sin x) \frac{1}{x}+\log x \cos x$
or $\qquad \begin{aligned}\frac{d y}{d x} & =y[\frac{\sin x}{x}+\cos x \log x] \& =x^{\sin x}[\frac{\sin x}{x}+\cos x \log x] \& =x^{\sin x-1} \cdot \sin x+x^{\sin x} \cdot \cos x \log x\end{aligned}$
Example 29 Find $\frac{d y}{d x}$, if $y^{x}+x^{y}+x^{x}=a^{b}$.
Solution Given that $y^{x}+x^{y}+x^{x}=a^{b}$.
Putting $u=y^{x}, v=x^{y}$ and $w=x^{x}$, we get $u+v+w=a^{b}$
Therefore $\qquad \frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}=0 \qquad \qquad (1)$
Now, $u=y^{x}$. Taking logarithm on both sides, we have
$$ \log u=x \log y $$
Differentiating both sides w.r.t. $x$, we have
$$ \begin{aligned} \frac{1}{u} \cdot \frac{d u}{d x} & =x \frac{d}{d x}(\log y)+\log y \frac{d}{d x}(x) \\ & =x \frac{1}{y} \cdot \frac{d y}{d x}+\log y \cdot 1 \\ \text{ So } \qquad \qquad \frac{d u}{d x} & =u(\frac{x}{y} \frac{d y}{d x}+\log y)=y^{x}[\frac{x}{y} \frac{d y}{d x}+\log y] \qquad \qquad (2) \end{aligned} $$
Also $v=x^{y} $
Taking logarithm on both sides, we have
$$ \log v=y \log x $$
Differentiating both sides w.r.t. $x$, we have
$$ \begin{aligned} \frac{1}{v} \cdot \frac{d v}{d x} & =y \frac{d}{d x}(\log x)+\log x \frac{d y}{d x} \\ & =y \cdot \frac{1}{x}+\log x \cdot \frac{d y}{d x} \\ \text{ So } \qquad \qquad \frac{d v}{d x} & =v[\frac{y}{x}+\log x \frac{d y}{d x}] \\ & =x^{y}[\frac{y}{x}+\log x \frac{d y}{d x}] \qquad \qquad (3) \end{aligned} $$
Again $ \qquad \qquad w=x^{x} $
Taking logarithm on both sides, we have
$$ \log w=x \log x $$
Differentiating both sides w.r.t. $x$, we have
$$ \begin{aligned} \frac{1}{w} \cdot \frac{d w}{d x} & =x \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}(x) \\ & =x \cdot \frac{1}{x}+\log x \cdot 1 \\ \end{aligned} $$
$$ \begin{aligned} \text{ i.e. } \qquad \qquad \frac{d w}{d x} & =w(1+\log x) \\ & =x^{x}(1+\log x) \qquad \qquad (4) \end{aligned} $$
From (1), (2), (3), (4), we have
$ y^{x}(\frac{x}{y} \frac{d y}{d x}+\log y)+x^{y}(\frac{y}{x}+\log x \frac{d y}{d x})+x^{x}(1+\log x)=0 $
or $\qquad(x \cdot y^{x-1}+x^{y} \cdot \log x) \frac{d y}{d x}=-x^{x}(1+\log x)-y \cdot x^{y-1}-y^{x} \log y$
Therefore $\qquad\frac{d y}{d x}=\frac{-[y^{x} \log y+y \cdot x^{y-1}+x^{x}(1+\log x)]}{x \cdot y^{x-1}+x^{y} \log x}$
EXERCISE 5.5
Differentiate the functions given in Exercises 1 to 11 w.r.t. $x$.
1. $\cos x \cdot \cos 2 x \cdot \cos 3 x$
Show Answer
Solution
Let $y=\cos x \cdot \cos 2 x \cdot \cos 3 x$
Taking logarithm on both the sides, we obtain
$\log y=\log (\cos x \cdot \cos 2 x \cdot \cos 3 x)$
$\Rightarrow \log y=\log (\cos x)+\log (\cos 2 x)+\log (\cos 3 x)$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{y} \frac{d y}{d x}=\frac{1}{\cos x} \cdot \frac{d}{d x}(\cos x)+\frac{1}{\cos 2 x} \cdot \frac{d}{d x}(\cos 2 x)+\frac{1}{\cos 3 x} \cdot \frac{d}{d x}(\cos 3 x) \\ & \Rightarrow \frac{d y}{d x}=y[-\frac{\sin x}{\cos x}-\frac{\sin 2 x}{\cos 2 x} \cdot \frac{d}{d x}(2 x)-\frac{\sin 3 x}{\cos 3 x} \cdot \frac{d}{d x}(3 x)] \\ & \therefore \frac{d y}{d x}=-\cos x \cdot \cos 2 x \cdot \cos 3 x[\tan x+2 \tan 2 x+3 \tan 3 x] \end{aligned} $
2. $\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}$
Show Answer
Solution
Let $y=\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}$
Taking logarithm on both the sides, we obtain
$ \begin{aligned} & \log y=\log \sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}} \\ & \Rightarrow \log y=\frac{1}{2} \log [\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}] \\ & \Rightarrow \log y=\frac{1}{2}[\log {(x-1)(x-2)}-\log {(x-3)(x-4)(x-5)}] \\ & \Rightarrow \log y=\frac{1}{2}[\log (x-1)+\log (x-2)-\log (x-3)-\log (x-4)-\log (x-5)] \end{aligned} $
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{y} \frac{d y}{d x}=\frac{1}{2} \begin{bmatrix} \frac{1}{x-1} \cdot \frac{d}{d x}(x-1)+\frac{1}{x-2} \cdot \frac{d}{d x}(x-2)-\frac{1}{x-3} \cdot \frac{d}{d x}(x-3) \\ -\frac{1}{x-4} \cdot \frac{d}{d x}(x-4)-\frac{1}{x-5} \cdot \frac{d}{d x}(x-5) \end{bmatrix} \\ & \Rightarrow \frac{d y}{d x}=\frac{y}{2}(\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5}) \\ & \therefore \frac{d y}{d x}=\frac{1}{2} \sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}[\frac{1}{x-1}+\frac{1}{x-2}-\frac{1}{x-3}-\frac{1}{x-4}-\frac{1}{x-5}] \end{aligned} $
3. $(\log x)^{\cos x}$
Show Answer
Solution
Let $y=(\log x)^{\cos x}$
Taking logarithm on both the sides, we obtain
$\log y=\cos x \cdot \log (\log x)$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{y} \cdot \frac{d y}{d x}=\frac{d}{d x}(\cos x) \times \log (\log x)+\cos x \times \frac{d}{d x}[\log (\log x)] \\ & \Rightarrow \frac{1}{y} \cdot \frac{d y}{d x}=-\sin x \log (\log x)+\cos x \times \frac{1}{\log x} \cdot \frac{d}{d x}(\log x) \\ & \Rightarrow \frac{d y}{d x}=y[-\sin x \log (\log x)+\frac{\cos x}{\log x} \times \frac{1}{x}] \\ & \therefore \frac{d y}{d x}=(\log x)^{\cos x}[\frac{\cos x}{x \log x}-\sin x \log (\log x)] \end{aligned} $
4. $x^{x}-2^{\sin x}$
Show Answer
Solution
Let $y=x^{x}-2^{\sin x}$
Also, let $x^{x}=u$ and $2^{\sin x}=v$
$\therefore y=u-v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}-\frac{d v}{d x}$
$u=x^{x}$
Taking logarithm on both the sides, we obtain
$\log u=x \log x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{u} \frac{d u}{d x}=[\frac{d}{d x}(x) \times \log x+x \times \frac{d}{d x}(\log x)]$
$\Rightarrow \frac{d u}{d x}=u[1 \times \log x+x \times \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=x^{x}(\log x+1)$
$\Rightarrow \frac{d u}{d x}=x^{x}(1+\log x)$
$v=2^{\sin x}$
Taking logarithm on both the sides with respect to $x$, we obtain $\log v=\sin x \cdot \log 2$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{v} \cdot \frac{d v}{d x}=\log 2 \cdot \frac{d}{d x}(\sin x)$
$\Rightarrow \frac{d v}{d x}=v \log 2 \cos x$
$\Rightarrow \frac{d v}{d x}=2^{\sin x} \cos x \log 2$
$\therefore \frac{d y}{d x}=x^{x}(1+\log x)-2^{\sin x} \cos x \log 2$
5. $(x+3)^{2} \cdot(x+4)^{3} \cdot(x+5)^{4}$
Show Answer
Solution
Let $y=(x+3)^{2} \cdot(x+4)^{3} \cdot(x+5)^{4}$
Taking logarithm on both the sides, we obtain
$ \begin{aligned} & \log y=\log (x+3)^{2}+\log (x+4)^{3}+\log (x+5)^{4} \\ & \Rightarrow \log y=2 \log (x+3)+3 \log (x+4)+4 \log (x+5) \end{aligned} $
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{y} \cdot \frac{d y}{d x}=2 \cdot \frac{1}{x+3} \cdot \frac{d}{d x}(x+3)+3 \cdot \frac{1}{x+4} \cdot \frac{d}{d x}(x+4)+4 \cdot \frac{1}{x+5} \cdot \frac{d}{d x}(x+5) \\ & \Rightarrow \frac{d y}{d x}=y[\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5}] \\ & \Rightarrow \frac{d y}{d x}=(x+3)^{2}(x+4)^{3}(x+5)^{4} \cdot[\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5}] \\ & \Rightarrow \frac{d y}{d x}=(x+3)^{2}(x+4)^{3}(x+5)^{4} \cdot[\frac{2(x+4)(x+5)+3(x+3)(x+5)+4(x+3)(x+4)}{(x+3)(x+4)(x+5)}] \\ & \Rightarrow \frac{d y}{d x}=(x+3)(x+4)^{2}(x+5)^{3} \cdot[2(x^{2}+9 x+20)+3(x^{2}+8 x+15)+4(x^{2}+7 x+12)] \\ & \therefore \frac{d y}{d x}=(x+3)(x+4)^{2}(x+5)^{3}(9 x^{2}+70 x+133) \end{aligned} $
6. $(x+\frac{1}{x})^{x}+x^{(1+\frac{1}{x})}$
Show Answer
Solution
Let $y=(x+\frac{1}{x})^{x}+x^{(1+\frac{1}{x})}$
Also, let $u=(x+\frac{1}{x})^{x}$ and $v=x^{(1+\frac{1}{x})}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
Then, $u=(x+\frac{1}{x})^{x}$
$\Rightarrow \log u=\log (x+\frac{1}{x})^{x}$
$\Rightarrow \log u=x \log (x+\frac{1}{x})$
Differentiating both sides with respect to $x$, we obtain $\frac{1}{u} \cdot \frac{d u}{d x}=\frac{d}{d x}(x) \times \log (x+\frac{1}{x})+x \times \frac{d}{d x}[\log (x+\frac{1}{x})]$
$\Rightarrow \frac{1}{u} \frac{d u}{d x}=1 \times \log (x+\frac{1}{x})+x \times \frac{1}{(x+\frac{1}{x})} \cdot \frac{d}{d x}(x+\frac{1}{x})$
$\Rightarrow \frac{d u}{d x}=u[\log (x+\frac{1}{x})+\frac{x}{(x+\frac{1}{x})} \times(1-\frac{1}{x^{2}})]$
$\Rightarrow \frac{d u}{d x}=(x+\frac{1}{x})^{x}[\log (x+\frac{1}{x})+\frac{(x-\frac{1}{x})}{(x+\frac{1}{x})}]$
$\Rightarrow \frac{d u}{d x}=(x+\frac{1}{x})^{x}[\log (x+\frac{1}{x})+\frac{x^{2}-1}{x^{2}+1}]$
$\Rightarrow \frac{d u}{d x}=(x+\frac{1}{x})^{x}[\frac{x^{2}-1}{x^{2}+1}+\log (x+\frac{1}{x})]$
$v=x^{(1+\frac{1}{x})}$
$\Rightarrow \log v=\log [x^{(1+\frac{1}{x})}]$
$\Rightarrow \log v=(1+\frac{1}{x}) \log x$
Differentiating both sides with respect to $x$, we obtain $\frac{1}{v} \cdot \frac{d v}{d x}=[\frac{d}{d x}(1+\frac{1}{x})] \times \log x+(1+\frac{1}{x}) \cdot \frac{d}{d x} \log x$
$\Rightarrow \frac{1}{v} \frac{d v}{d x}=(-\frac{1}{x^{2}}) \log x+(1+\frac{1}{x}) \cdot \frac{1}{x}$
$\Rightarrow \frac{1}{v} \frac{d v}{d x}=-\frac{\log x}{x^{2}}+\frac{1}{x}+\frac{1}{x^{2}}$
$\Rightarrow \frac{d v}{d x}=v[\frac{-\log x+x+1}{x^{2}}]$
$\Rightarrow \frac{d v}{d x}=x^{(1+\frac{1}{x})}(\frac{x+1-\log x}{x^{2}})$
Therefore, from (1), (2), and (3), we obtain
$\frac{d y}{d x}=(x+\frac{1}{x})^{x}[\frac{x^{2}-1}{x^{2}+1}+\log (x+\frac{1}{x})]+x^{(1+\frac{1}{x})}(\frac{x+1-\log x}{x^{2}})$
7. $(\log x)^{x}+x^{\log x}$
Show Answer
Solution
Let $y=(\log x)^{x}+x^{\log x}$
Also, let $u=(\log x)^{x}$ and $v=x^{\log x}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=(\log x)^{x}$
$\Rightarrow \log u=\log [(\log x)^{x}]$
$\Rightarrow \log u=x \log (\log x)$
Differentiating both sides with respect to $x$, we obtain $\frac{1}{u} \frac{d u}{d x}=\frac{d}{d x}(x) \times \log (\log x)+x \cdot \frac{d}{d x}[\log (\log x)]$
$\Rightarrow \frac{d u}{d x}=u[1 \times \log (\log x)+x \cdot \frac{1}{\log x} \cdot \frac{d}{d x}(\log x)]$
$\Rightarrow \frac{d u}{d x}=(\log x)^{x}[\log (\log x)+\frac{x}{\log x} \cdot \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=(\log x)^{x}[\log (\log x)+\frac{1}{\log x}]$
$\Rightarrow \frac{d u}{d x}=(\log x)^{x}[\frac{\log (\log x) \cdot \log x+1}{\log x}]$
$\Rightarrow \frac{d u}{d x}=(\log x)^{x-1}[1+\log x \cdot \log (\log x)]$
$v=x^{\log x}$
$\Rightarrow \log v=\log (x^{\log x})$
$\Rightarrow \log v=\log x \log x=(\log x)^{2}$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{v} \cdot \frac{d v}{d x}=\frac{d}{d x}[(\log x)^{2}]$
$\Rightarrow \frac{1}{v} \cdot \frac{d v}{d x}=2(\log x) \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{d v}{d x}=2 v(\log x) \cdot \frac{1}{x}$
$\Rightarrow \frac{d v}{d x}=2 x^{\log x} \frac{\log x}{x}$
$\Rightarrow \frac{d v}{d x}=2 x^{\log x-1} \cdot \log x$
Therefore, from (1), (2), and (3), we obtain
$\frac{d y}{d x}=(\log x)^{x-1}[1+\log x \cdot \log (\log x)]+2 x^{\log x-1} \cdot \log x$
8. $(\sin x)^{x}+\sin ^{-1} \sqrt{x}$
Show Answer
Solution
Let $y=(\sin x)^{x}+\sin ^{-1} \sqrt{x}$
Also, let $u=(\sin x)^{x}$ and $v=\sin ^{-1} \sqrt{x}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=(\sin x)^{x}$
$\Rightarrow \log u=\log (\sin x)^{x}$
$\Rightarrow \log u=x \log (\sin x)$
Differentiating both sides with respect to $x$, we obtain
$\Rightarrow \frac{1}{u} \frac{d u}{d x}=\frac{d}{d x}(x) \times \log (\sin x)+x \times \frac{d}{d x}[\log (\sin x)]$
$\Rightarrow \frac{d u}{d x}=u[1 \cdot \log (\sin x)+x \cdot \frac{1}{\sin x} \cdot \frac{d}{d x}(\sin x)]$
$\Rightarrow \frac{d u}{d x}=(\sin x)^{x}[\log (\sin x)+\frac{x}{\sin x} \cdot \cos x]$
$\Rightarrow \frac{d u}{d x}=(\sin x)^{x}(x \cot x+\log \sin x)$
$v=\sin ^{-1} \sqrt{x}$
Differentiating both sides with respect to $x$, we obtain
$\frac{d v}{d x}=\frac{1}{\sqrt{1-(\sqrt{x})^{2}}} \cdot \frac{d}{d x}(\sqrt{x})$
$\Rightarrow \frac{d v}{d x}=\frac{1}{\sqrt{1-x}} \cdot \frac{1}{2 \sqrt{x}}$
$\Rightarrow \frac{d v}{d x}=\frac{1}{2 \sqrt{x-x^{2}}}$
Therefore, from (1), (2), and (3), we obtain
$\frac{d y}{d x}=(\sin x)^{x}(x \cot x+\log \sin x)+\frac{1}{2 \sqrt{x-x^{2}}}$
9. $x^{\sin x}+(\sin x)^{\cos x}$
Show Answer
Solution
Let $y=x^{\sin x}+(\sin x)^{\cos x}$
Also, let $u=x^{\sin x}$ and $v=(\sin x)^{\cos x}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=x^{\sin x}$
$\Rightarrow \log u=\log (x^{\sin x})$
$\Rightarrow \log u=\sin x \log x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{u} \frac{d u}{d x}=\frac{d}{d x}(\sin x) \cdot \log x+\sin x \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{d u}{d x}=u[\cos x \log x+\sin x \cdot \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=x^{\sin x}[\cos x \log x+\frac{\sin x}{x}]$
$v=(\sin x)^{\cos x}$
$\Rightarrow \log v=\log (\sin x)^{\cos x}$
$\Rightarrow \log v=\cos x \log (\sin x)$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{v} \frac{d v}{d x}=\frac{d}{d x}(\cos x) \times \log (\sin x)+\cos x \times \frac{d}{d x}[\log (\sin x)]$
$\Rightarrow \frac{d v}{d x}=v[-\sin x \cdot \log (\sin x)+\cos x \cdot \frac{1}{\sin x} \cdot \frac{d}{d x}(\sin x)]$
$\Rightarrow \frac{d v}{d x}=(\sin x)^{\cos x}[-\sin x \log \sin x+\frac{\cos x}{\sin x} \cos x]$
$\Rightarrow \frac{d v}{d x}=(\sin x)^{\cos x}[-\sin x \log \sin x+\cot x \cos x]$
$\Rightarrow \frac{d v}{d x}=(\sin x)^{\cos x}[\cot x \cos x-\sin x \log \sin x]$
From (1), (2), and (3), we obtain
$\frac{d y}{d x}=x^{\sin x}(\cos x \log x+\frac{\sin x}{x})+(\sin x)^{\cos x}[\cos x \cot x-\sin x \log \sin x]$
10. $x^{x \cos x}+\frac{x^{2}+1}{x^{2}-1}$
Show Answer
Solution
Let $y=x^{x \cos x}+\frac{x^{2}+1}{x^{2}-1}$
Also, let $u=x^{x \cos x}$ and $v=\frac{x^{2}+1}{x^{2}-1}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=x^{x \cos x}$
$\Rightarrow \log u=\log (x^{x \cos x})$
$\Rightarrow \log u=x \cos x \log x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{u} \frac{d u}{d x}=\frac{d}{d x}(x) \cdot \cos x \cdot \log x+x \cdot \frac{d}{d x}(\cos x) \cdot \log x+x \cos x \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{d u}{d x}=u[1 \cdot \cos x \cdot \log x+x \cdot(-\sin x) \log x+x \cos x \cdot \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=x^{x \cos x}(\cos x \log x-x \sin x \log x+\cos x)$
$\Rightarrow \frac{d u}{d x}=x^{x \cos x}[\cos x(1+\log x)-x \sin x \log x]$
$v=\frac{x^{2}+1}{x^{2}-1}$
$\Rightarrow \log v=\log (x^{2}+1)-\log (x^{2}-1)$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{v} \frac{d v}{d x}=\frac{2 x}{x^{2}+1}-\frac{2 x}{x^{2}-1}$
$\Rightarrow \frac{d v}{d x}=v[\frac{2 x(x^{2}-1)-2 x(x^{2}+1)}{(x^{2}+1)(x^{2}-1)}]$
$\Rightarrow \frac{d v}{d x}=\frac{x^{2}+1}{x^{2}-1} \times[\frac{-4 x}{(x^{2}+1)(x^{2}-1)}]$
$\Rightarrow \frac{d v}{d x}=\frac{-4 x}{(x^{2}-1)^{2}}$
From (1), (2), and (3), we obtain
$\frac{d y}{d x}=x^{x \cos x}[\cos x(1+\log x)-x \sin x \log x]-\frac{4 x}{(x^{2}-1)^{2}}$
11. $(x \cos x)^{x}+(x \sin x)^{\frac{1}{x}}$
Show Answer
Solution
Let $y=(x \cos x)^{x}+(x \sin x)^{\frac{1}{x}}$
Also, let $u=(x \cos x)^{x}$ and $v=(x \sin x)^{\frac{1}{x}}$
$\therefore y=u+v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=(x \cos x)^{x}$
$\Rightarrow \log u=\log (x \cos x)^{x}$
$\Rightarrow \log u=x \log (x \cos x)$
$\Rightarrow \log u=x[\log x+\log \cos x]$
$\Rightarrow \log u=x \log x+x \log \cos x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{u} \frac{d u}{d x}=\frac{d}{d x}(x \log x)+\frac{d}{d x}(x \log \cos x)$
$\Rightarrow \frac{d u}{d x}=u[{\log x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log x)}+{\log \cos x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log \cos x)}]$
$\Rightarrow \frac{d u}{d x}=(x \cos x)^{x}[(\log x \cdot 1+x \cdot \frac{1}{x})+{\log \cos x \cdot 1+x \cdot \frac{1}{\cos x} \cdot \frac{d}{d x}(\cos x)}]$
$\Rightarrow \frac{d u}{d x}=(x \cos x)^{x}[(\log x+1)+{\log \cos x+\frac{x}{\cos x} \cdot(-\sin x)}]$
$\Rightarrow \frac{d u}{d x}=(x \cos x)^{x}[(1+\log x)+(\log \cos x-x \tan x)]$
$\Rightarrow \frac{d u}{d x}=(x \cos x)^{x}[1-x \tan x+(\log x+\log \cos x)]$
$\Rightarrow \frac{d u}{d x}=(x \cos x)^{x}[1-x \tan x+\log (x \cos x)]$
$ \begin{aligned} & v=(x \sin x)^{\frac{1}{x}} \\ & \Rightarrow \log v=\log (x \sin x)^{\frac{1}{x}} \\ & \Rightarrow \log v=\frac{1}{x} \log (x \sin x) \\ & \Rightarrow \log v=\frac{1}{x}(\log x+\log \sin x) \\ & \Rightarrow \log v=\frac{1}{x} \log x+\frac{1}{x} \log \sin x \end{aligned} $
Differentiating both sides with respect to $x$, we obtain
$$ \begin{align*} & \frac{1}{v} \frac{d v}{d x}=\frac{d}{d x}(\frac{1}{x} \log x)+\frac{d}{d x}[\frac{1}{x} \log (\sin x)] \\ & \Rightarrow \frac{1}{v} \frac{d v}{d x}=[\log x \cdot \frac{d}{d x}(\frac{1}{x})+\frac{1}{x} \cdot \frac{d}{d x}(\log x)]+[\log (\sin x) \cdot \frac{d}{d x}(\frac{1}{x})+\frac{1}{x} \cdot \frac{d}{d x}{\log (\sin x)}] \\ & \Rightarrow \frac{1}{v} \frac{d v}{d x}=[\log x \cdot(-\frac{1}{x^{2}})+\frac{1}{x}+\frac{1}{x}]+[\log (\sin x) \cdot(-\frac{1}{x^{2}})+\frac{1}{x} \cdot \frac{1}{\sin x} \cdot \frac{d}{d x}(\sin x)] \\ & \Rightarrow \frac{1}{v} \frac{d v}{d x}=\frac{1}{x^{2}}(1-\log x)+[-\frac{\log (\sin x)}{x^{2}}+\frac{1}{x \sin x} \cdot \cos x] \\ & \Rightarrow \frac{d v}{d x}=(x \sin x)^{\frac{1}{x}}[\frac{1-\log x}{x^{2}}+\frac{-\log (\sin x)+x \cot x}{x^{2}}] \\ & \Rightarrow \frac{d v}{d x}=(x \sin x)^{\frac{1}{x}}[\frac{1-\log x-\log (\sin x)+x \cot x}{x^{2}}] \\ & \Rightarrow \frac{d v}{d x}=(x \sin x)^{\frac{1}{x}}[\frac{1-\log (x \sin x)+x \cot x}{x^{2}}] \tag{3} \end{align*} $$
From (1), (2), and (3), we obtain
$\frac{d y}{d x}=(x \cos x)^{x}[1-x \tan x+\log (x \cos x)]+(x \sin x)^{\frac{1}{x}}[\frac{x \cot x+1-\log (x \sin x)}{x^{2}}]$
Find $\frac{d y}{d x}$ of the functions given in Exercises 12 to 15 .
12. $x^{y}+y^{x}=1$
Show Answer
Solution
The given function is $x^{y}+y^{x}=1$
Let $x^{y}=u$ and $y^{x}=v$
Then, the function becomes $u+v=1$
$\therefore \frac{d u}{d x}+\frac{d v}{d x}=0$
$u=x^{y}$
$\Rightarrow \log u=\log (x^{y})$
$\Rightarrow \log u=y \log x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{u} \frac{d u}{d x}=\log x \frac{d y}{d x}+y \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{d u}{d x}=u[\log x \frac{d y}{d x}+y \cdot \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=x^{y}(\log x \frac{d y}{d x}+\frac{y}{x})$
$v=y^{x}$
$\Rightarrow \log v=\log (y^{x})$
$\Rightarrow \log v=x \log y$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{v} \cdot \frac{d v}{d x}=\log y \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log y)$
$\Rightarrow \frac{d v}{d x}=v(\log y \cdot 1+x \cdot \frac{1}{y} \cdot \frac{d y}{d x})$
$\Rightarrow \frac{d v}{d x}=y^{x}(\log y+\frac{x}{y} \frac{d y}{d x})$
From (1), (2), and (3), we obtain
$ \begin{aligned} & x^{y}(\log x \frac{d y}{d x}+\frac{y}{x})+y^{x}(\log y+\frac{x}{y} \frac{d y}{d x})=0 \\ & \Rightarrow(x^{y} \log x+x y^{x-1}) \frac{d y}{d x}=-(y x^{y-1}+y^{x} \log y) \\ & \therefore \frac{d y}{d x}=-\frac{y x^{y-1}+y^{x} \log y}{x^{y} \log x+x y^{x-1}} \end{aligned} $
13. $(\cos x)^{y}=(\cos y)^{x}$
Show Answer
Solution
The given function is $(\cos x)^{y}=(\cos y)^{x}$
Taking logarithm on both the sides, we obtain
$y \log \cos x=x \log \cos y$
Differentiating both sides, we obtain
$\log \cos x \cdot \frac{d y}{d x}+y \cdot \frac{d}{d x}(\log \cos x)=\log \cos y \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log \cos y)$
$\Rightarrow \log \cos x \frac{d y}{d x}+y \cdot \frac{1}{\cos x} \cdot \frac{d}{d x}(\cos x)=\log \cos y \cdot 1+x \cdot \frac{1}{\cos y} \cdot \frac{d}{d x}(\cos y)$
$\Rightarrow \log \cos x \frac{d y}{d x}+\frac{y}{\cos x} \cdot(-\sin x)=\log \cos y+\frac{x}{\cos y}(-\sin y) \cdot \frac{d y}{d x}$
$\Rightarrow \log \cos x \frac{d y}{d x}-y \tan x=\log \cos y-x \tan y \frac{d y}{d x}$
$\Rightarrow(\log \cos x+x \tan y) \frac{d y}{d x}=y \tan x+\log \cos y$
$\therefore \frac{d y}{d x}=\frac{y \tan x+\log \cos y}{x \tan y+\log \cos x}$
14. $y^{x}=x^{y}$
Show Answer
Solution
The given function is $y^{x}=x^{y}$
Taking logarithm on both the sides, we obtain
$x \log y=y \log x$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \log y \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log y)=\log x \cdot \frac{d}{d x}(y)+y \cdot \frac{d}{d x}(\log x) \\ & \Rightarrow \log y \cdot 1+x \cdot \frac{1}{y} \cdot \frac{d y}{d x}=\log x \cdot \frac{d y}{d x}+y \cdot \frac{1}{x} \\ & \Rightarrow \log y+\frac{x}{y} \frac{d y}{d x}=\log x \frac{d y}{d x}+\frac{y}{x} \\ & \Rightarrow(\frac{x}{y}-\log x) \frac{d y}{d x}=\frac{y}{x}-\log y \\ & \Rightarrow(\frac{x-y \log x}{y}) \frac{d y}{d x}=\frac{y-x \log y}{x} \\ & \therefore \frac{d y}{d x}=\frac{y}{x}(\frac{y-x \log y}{x-y \log x}) \end{aligned} $
15. $x y=e^{(x-y)}$
Show Answer
Solution
The given function is $x y=e^{(x-y)}$
Taking logarithm on both the sides, we obtain
$ \begin{aligned} & \log (x y)=\log (e^{x-y}) \\ & \Rightarrow \log x+\log y=(x-y) \log e \\ & \Rightarrow \log x+\log y=(x-y) \times 1 \\ & \Rightarrow \log x+\log y=x-y \end{aligned} $
Differentiating both sides with respect to $x$, we obtain
$\frac{d}{d x}(\log x)+\frac{d}{d x}(\log y)=\frac{d}{d x}(x)-\frac{d y}{d x}$
$\Rightarrow \frac{1}{x}+\frac{1}{y} \frac{d y}{d x}=1-\frac{d y}{d x}$
$\Rightarrow(1+\frac{1}{y}) \frac{d y}{d x}=1-\frac{1}{x}$
$\Rightarrow(\frac{y+1}{y}) \frac{d y}{d x}=\frac{x-1}{x}$
$\therefore \frac{d y}{d x}=\frac{y(x-1)}{x(y+1)}$
16. Find the derivative of the function given by $f(x)=(1+x)(1+x^{2})(1+x^{4})(1+x^{8})$ and hence find $f^{\prime}(1)$.
Show Answer
Solution
The given relationship is $f(x)=(1+x)(1+x^{2})(1+x^{4})(1+x^{8})$
Taking logarithm on both the sides, we obtain
$\log f(x)=\log (1+x)+\log (1+x^{2})+\log (1+x^{4})+\log (1+x^{8})$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{f(x)} \cdot \frac{d}{d x}[f(x)]=\frac{d}{d x} \log (1+x)+\frac{d}{d x} \log (1+x^{2})+\frac{d}{d x} \log (1+x^{4})+\frac{d}{d x} \log (1+x^{8}) \\ & \Rightarrow \frac{1}{f(x)} \cdot f^{\prime}(x)=\frac{1}{1+x} \cdot \frac{d}{d x}(1+x)+\frac{1}{1+x^{2}} \cdot \frac{d}{d x}(1+x^{2})+\frac{1}{1+x^{4}} \cdot \frac{d}{d x}(1+x^{4})+\frac{1}{1+x^{8}} \cdot \frac{d}{d x}(1+x^{8}) \\ & \Rightarrow f^{\prime}(x)=f(x)[\frac{1}{1+x}+\frac{1}{1+x^{2}} \cdot 2 x+\frac{1}{1+x^{4}} \cdot 4 x^{3}+\frac{1}{1+x^{8}} \cdot 8 x^{7}] \\ & \begin{matrix} \therefore f^{\prime}(x)=(1+x)(1+x^{2})(1+x^{4})(1+x^{8})[\frac{1}{1+x}+\frac{2 x}{1+x^{2}}+\frac{4 x^{3}}{1+x^{4}}+\frac{8 x^{7}}{1+x^{8}}] \\ \text{ Hence, } f^{\prime}(1)=(1+1)(1+1^{2})(1+1^{4})(1+1^{8})[\frac{1}{1+1}+\frac{2 \times 1}{1+1^{2}}+\frac{4 \times 1^{3}}{1+1^{4}}+\frac{8 \times 1^{7}}{1+1^{8}}] \\ =2 \times 2 \times 2 \times 2[\frac{1}{2}+\frac{2}{2}+\frac{4}{2}+\frac{8}{2}] \\ =16 \times(\frac{1+2+4+8}{2}) \\ =16 \times \frac{15}{2}=120 \end{matrix} \end{aligned} $
17. Differentiate $(x^{2}-5 x+8)(x^{3}+7 x+9)$ in three ways mentioned below:
(i) by using product rule
(ii) by expanding the product to obtain a single polynomial.
(iii) by logarithmic differentiation.
Do they all give the same answer?
Show Answer
Solution
(i) Let $y=(x^{5}-5 x+8)(x^{3}+7 x+9)$
Let $x^{2}-5 x+8=u$ and $x^{3}+7 x+9=v$
$\therefore y=u v$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x} \cdot v+u \cdot \frac{d v}{d x} \quad$ (By using product rule)
$\Rightarrow \frac{d y}{d x}=\frac{d}{d x}(x^{2}-5 x+8) \cdot(x^{3}+7 x+9)+(x^{2}-5 x+8) \cdot \frac{d}{d x}(x^{3}+7 x+9)$
$\Rightarrow \frac{d y}{d x}=(2 x-5)(x^{3}+7 x+9)+(x^{2}-5 x+8)(3 x^{2}+7)$
$\Rightarrow \frac{d y}{d x}=2 x(x^{3}+7 x+9)-5(x^{3}+7 x+9)+x^{2}(3 x^{2}+7)-5 x(3 x^{2}+7)+8(3 x^{2}+7)$
$\Rightarrow \frac{d y}{d x}=(2 x^{4}+14 x^{2}+18 x)-5 x^{3}-35 x-45+(3 x^{4}+7 x^{2})-15 x^{3}-35 x+24 x^{2}+56$
$\therefore \frac{d y}{d x}=5 x^{4}-20 x^{3}+45 x^{2}-52 x+11$
(ii) $y=(x^{2}-5 x+8)(x^{3}+7 x+9)$
$ \begin{aligned} & =x^{2}(x^{3}+7 x+9)-5 x(x^{3}+7 x+9)+8(x^{3}+7 x+9) \\ & =x^{5}+7 x^{3}+9 x^{2}-5 x^{4}-35 x^{2}-45 x+8 x^{3}+56 x+72 \\ & =x^{5}-5 x^{4}+15 x^{3}-26 x^{2}+11 x+72 \\ & \therefore \frac{d y}{d x}=\frac{d}{d x}(x^{5}-5 x^{4}+15 x^{3}-26 x^{2}+11 x+72) \\ & =\frac{d}{d x}(x^{5})-5 \frac{d}{d x}(x^{4})+15 \frac{d}{d x}(x^{3})-26 \frac{d}{d x}(x^{2})+11 \frac{d}{d x}(x)+\frac{d}{d x}(72) \\ & =5 x^{4}-5 \times 4 x^{3}+15 \times 3 x^{2}-26 \times 2 x+11 \times 1+0 \\ & =5 x^{4}-20 x^{3}+45 x^{2}-52 x+11 \end{aligned} $
(iii) $y=(x^{2}-5 x+8)(x^{3}+7 x+9)$
Taking logarithm on both the sides, we obtain
$\log y=\log (x^{2}-5 x+8)+\log (x^{3}+7 x+9)$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{1}{y} \frac{d y}{d x}=\frac{d}{d x} \log (x^{2}-5 x+8)+\frac{d}{d x} \log (x^{3}+7 x+9) \\ & \Rightarrow \frac{1}{y} \frac{d y}{d x}=\frac{1}{x^{2}-5 x+8} \cdot \frac{d}{d x}(x^{2}-5 x+8)+\frac{1}{x^{3}+7 x+9} \cdot \frac{d}{d x}(x^{3}+7 x+9) \\ & \Rightarrow \frac{d y}{d x}=y[\frac{1}{x^{2}-5 x+8} \times(2 x-5)+\frac{1}{x^{3}+7 x+9} \times(3 x^{2}+7)] \\ & \Rightarrow \frac{d y}{d x}=(x^{2}-5 x+8)(x^{3}+7 x+9)[\frac{2 x-5}{x^{2}-5 x+8}+\frac{3 x^{2}+7}{x^{3}+7 x+9}] \\ & \Rightarrow \frac{d y}{d x}=(x^{2}-5 x+8)(x^{3}+7 x+9)[\frac{(2 x-5)(x^{3}+7 x+9)+(3 x^{2}+7)(x^{2}-5 x+8)}{(x^{2}-5 x+8)(x^{3}+7 x+9)}] \\ & \Rightarrow \frac{d y}{d x}=2 x(x^{3}+7 x+9)-5(x^{3}+7 x+9)+3 x^{2}(x^{2}-5 x+8)+7(x^{2}-5 x+8) \\ & \Rightarrow \frac{d y}{d x}=(2 x^{4}+14 x^{2}+18 x)-5 x^{3}-35 x-45+(3 x^{4}-15 x^{3}+24 x^{2})+(7 x^{2}-35 x+56) \\ & \Rightarrow \frac{d y}{d x}=5 x^{4}-20 x^{3}+45 x^{2}-52 x+11 \end{aligned} $
From the above three observations, it can be concluded that all the results of $\frac{d y}{d x}$ are same.
18. If $u, v$ and $w$ are functions of $x$, then show that in two ways - first by repeated application of product rule, second by logarithmic differentiation.
$ \frac{d}{d x}(u . v \cdot w)=\frac{d u}{d x} v \cdot w+u \cdot \frac{d v}{d x} \cdot w+u \cdot v \frac{d w}{d x} $
Show Answer
Solution
Let $y=u . v . w=u .(v . w)$
By applying product rule, we obtain $\frac{d y}{d x}=\frac{d u}{d x} \cdot(v \cdot w)+u \cdot \frac{d}{d x}(v \cdot w)$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x} v \cdot w+u[\frac{d v}{d x} \cdot w+v \cdot \frac{d w}{d x}] \quad$ (Again applying product rule)
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x} \cdot v \cdot w+u \cdot \frac{d v}{d x} \cdot w+u \cdot v \cdot \frac{d w}{d x}$
By taking logarithm on both sides of the equation $y=u . v . w$, we obtain
$\log y=\log u+\log v+\log w$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{y} \cdot \frac{d y}{d x}=\frac{d}{d x}(\log u)+\frac{d}{d x}(\log v)+\frac{d}{d x}(\log w)$
$\Rightarrow \frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{u} \frac{d u}{d x}+\frac{1}{v} \frac{d v}{d x}+\frac{1}{w} \frac{d w}{d x}$
$\Rightarrow \frac{d y}{d x}=y(\frac{1}{u} \frac{d u}{d x}+\frac{1}{v} \frac{d v}{d x}+\frac{1}{w} \frac{d w}{d x})$
$\Rightarrow \frac{d y}{d x}=u . v . w \cdot(\frac{1}{u} \frac{d u}{d x}+\frac{1}{v} \frac{d v}{d x}+\frac{1}{w} \frac{d w}{d x})$
$\therefore \frac{d y}{d x}=\frac{d u}{d x} \cdot v \cdot w+u \cdot \frac{d v}{d x} \cdot w+u \cdot v \cdot \frac{d w}{d x}$
5.6 Derivatives of Functions in Parametric Forms
Sometimes the relation between two variables is neither explicit nor implicit, but some link of a third variable with each of the two variables, separately, establishes a relation between the first two variables. In such a situation, we say that the relation between them is expressed via a third variable. The third variable is called the parameter. More precisely, a relation expressed between two variables $x$ and $y$ in the form $x=f(t), y=g(t)$ is said to be parametric form with $t$ as a parameter.
In order to find derivative of function in such form, we have by chain rule.
$$ \begin{aligned} & \frac{d y}{d t}=\frac{d y}{d x} \cdot \frac{d x}{d t} \\ \end{aligned} $$
or $\qquad\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}(\text{whenever } \frac{d x}{d t} \neq 0)$
Thus $\qquad \frac{d y}{d x}=\frac{g^{\prime}(t)}{f^{\prime}(t)}(\text{ as } \frac{d y}{d t}=g^{\prime}(t) \text{ and } \frac{d x}{d t}=f^{\prime}(t)) [\text{ provided } f^{\prime}(t) \neq 0]$
Example 30 Find $\frac{d y}{d x}$, if $x=a \cos \theta, y=a \sin \theta$.
Solution Given that
$$ x=a \cos \theta, y=a \sin \theta $$
Therefore $\quad \frac{d x}{d \theta}=-a \sin \theta, \frac{d y}{d \theta}=a \cos \theta$
Hence $\quad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{a \cos \theta}{-a \sin \theta}=-\cot \theta$
Example 31 Find $\frac{d y}{d x}$, if $x=a t^{2}, y=2 a t$.
Solution Given that $x=a t^{2}, y=2 a t$
So $\qquad \frac{d x}{d t}=2 a t \text { or } \frac{d y}{d t}=2 a$
Therefore $ \qquad \frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{2 a}{2 a t}=\frac{1}{t}$
Example 32 Find $\frac{d y}{d x}$, if $x=a(\theta+\sin \theta), y=a(1-\cos \theta)$.
Solution We have $\frac{d x}{d \theta}=a(1+\cos \theta), \frac{d y}{d \theta}=a(\sin \theta)$
Therefore $\qquad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{a \sin\theta}{a(1+\cos \theta)}=\tan \frac{\theta}{2}$
Note It may be noted here that $\frac{d y}{d x}$ is expressed in terms of parameter only without directly involving the main variables $x$ and $y$.
Example 33 Find $\frac{d y}{d x}$, if $x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$.
Solution Let $x=a \cos ^{3} \theta, y=a \sin ^{3} \theta$. Then
$$ \begin{aligned} x^{\frac{2}{3}}+y^{\frac{3}{2}} & =\left(a \cos ^{3} \theta\right)^{\frac{2}{3}}+\left(a \sin ^{3} \theta\right)^{\frac{2}{3}} \\ & =a^{\frac{2}{3}}\left(\cos ^{2} \theta+\left(\sin ^{2} \theta\right)=a^{\frac{2}{3}}\right. \end{aligned} $$
Hence, $x=a \cos ^{3} \theta, y=a \sin ^{3} \theta$ is parametric equation of $x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$
Now $\qquad \frac{d x}{d \theta}=-3 a \cos ^{2} \theta \sin \theta \text{ and } \frac{d y}{d\theta}=3 a \sin ^{2} \theta \cos \theta$
Therefore $\quad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{3 a \sin ^{2} \theta \cos \theta}{-3 a \cos ^{2} \theta \sin \theta}=-\tan \theta=-\sqrt[3]{\frac{y}{x}}$
EXERCISE 5.6
If $x$ and $y$ are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find $\frac{d y}{d x}$.
1. $x=2 a t^{2}, y=a t^{4}$
Show Answer
Solution
The given equations are $x=2 a t^{2}$ and $y=a t^{4}$
Then, $\frac{d x}{d t}=\frac{d}{d t}(2 a t^{2})=2 a \cdot \frac{d}{d t}(t^{2})=2 a \cdot 2 t=4 a t$
$\frac{d y}{d t}=\frac{d}{d t}(a t^{4})=a \cdot \frac{d}{d t}(t^{4})=a \cdot 4 \cdot t^{3}=4 a t^{3}$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{4 a t^{3}}{4 a t}=t^{2}$
2. $x=a \cos \theta, y=b \cos \theta$
Show Answer
Solution
The given equations are $x=a \cos \theta$ and $y=b \cos \theta$
Then, $\frac{d x}{d \theta}=\frac{d}{d \theta}(a \cos \theta)=a(-\sin \theta)=-a \sin \theta$
$\frac{d y}{d \theta}=\frac{d}{d \theta}(b \cos \theta)=b(-\sin \theta)=-b \sin \theta$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d \theta})}{(\frac{d x}{d \theta})}=\frac{-b \sin \theta}{-a \sin \theta}=\frac{b}{a}$
3. $x=\sin t, y=\cos 2 t$
Show Answer
Solution
The given equations are $x=\sin t$ and $y=\cos 2 t$
Then, $\frac{d x}{d t}=\frac{d}{d t}(\sin t)=\cos t$
$\frac{d y}{d t}=\frac{d}{d t}(\cos 2 t)=-\sin 2 t \cdot \frac{d}{d t}(2 t)=-2 \sin 2 t$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{-2 \sin 2 t}{\cos t}=\frac{-2 \cdot 2 \sin t \cos t}{\cos t}=-4 \sin t$
4. $x=4 t, y=\frac{4}{t}$
Show Answer
Solution
The given equations are $x=4 t$ and $y=\frac{4}{t}$
$ \begin{aligned} & \frac{d x}{d t}=\frac{d}{d t}(4 t)=4 \\ & \frac{d y}{d t}=\frac{d}{d t}(\frac{4}{t})=4 \cdot \frac{d}{d t}(\frac{1}{t})=4 \cdot(\frac{-1}{t^{2}})=\frac{-4}{t^{2}} \\ & \therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{(\frac{-4}{t^{2}})}{4}=\frac{-1}{t^{2}} \end{aligned} $
5. $x=\cos \theta-\cos 2 \theta, y=\sin \theta-\sin 2 \theta$
Show Answer
Solution
The given equations are $x=\cos \theta-\cos 2 \theta$ and $y=\sin \theta-\sin 2 \theta$
Then, $\frac{d x}{d \theta}=\frac{d}{d \theta}(\cos \theta-\cos 2 \theta)=\frac{d}{d \theta}(\cos \theta)-\frac{d}{d \theta}(\cos 2 \theta)$
$ =-\sin \theta-(-2 \sin 2 \theta)=2 \sin 2 \theta-\sin \theta $
$\frac{d y}{d \theta}=\frac{d}{d \theta}(\sin \theta-\sin 2 \theta)=\frac{d}{d \theta}(\sin \theta)-\frac{d}{d \theta}(\sin 2 \theta)$
$=\cos \theta-2 \cos 2 \theta$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d \theta})}{(\frac{d x}{d \theta})}=\frac{\cos \theta-2 \cos 2 \theta}{2 \sin 2 \theta-\sin \theta}$
6. $x=a(\theta-\sin \theta), y=a(1+\cos \theta)$
Show Answer
Solution
The given equations are $x=a(\theta-\sin \theta)$ and $y=a(1+\cos \theta)$
Then, $\frac{d x}{d \theta}=a[\frac{d}{d \theta}(\theta)-\frac{d}{d \theta}(\sin \theta)]=a(1-\cos \theta)$
$\frac{d y}{d \theta}=a[\frac{d}{d \theta}(1)+\frac{d}{d \theta}(\cos \theta)]=a[0+(-\sin \theta)]=-a \sin \theta$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d \theta})}{(\frac{d x}{d \theta})}=\frac{-a \sin \theta}{a(1-\cos \theta)}=\frac{-2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}}{2 \sin ^{2} \frac{\theta}{2}}=\frac{-\cos \frac{\theta}{2}}{\sin \frac{\theta}{2}}=-\cot \frac{\theta}{2}$
7. $x=\frac{\sin ^{3} t}{\sqrt{\cos 2 t}}, y=\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}$
Show Answer
Solution
The given equations are $x=\frac{\sin ^{3} t}{\sqrt{\cos 2 t}}$ and $y=\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}$
$ \begin{aligned} & \text{ Then, } \frac{d x}{d t}=\frac{d}{d t}[\frac{\sin ^{3} t}{\sqrt{\cos 2 t}}] \\ & =\frac{\sqrt{\cos 2 t} \cdot \frac{d}{d t}(\sin ^{3} t)-\sin ^{3} t \cdot \frac{d}{d t} \sqrt{\cos 2 t}}{\cos 2 t} \\ & =\frac{\sqrt{\cos 2 t} \cdot 3 \sin ^{2} t \cdot \frac{d}{d t}(\sin t)-\sin ^{3} t \times \frac{1}{2 \sqrt{\cos 2 t}} \cdot \frac{d}{d t}(\cos 2 t)}{\cos 2 t} \\ & =\frac{3 \sqrt{\cos 2 t} \cdot \sin ^{2} t \cos t-\frac{\sin ^{3} t}{2 \sqrt{\cos 2 t}} \cdot(-2 \sin 2 t)}{\cos 2 t} \\ & =\frac{3 \cos 2 t \sin ^{2} t \cos t+\sin ^{3} t \sin 2 t}{\cos 2 t \sqrt{\cos 2 t}} \\ & \frac{d y}{d t}=\frac{d}{d t}[\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}] \\ & =\frac{\sqrt{\cos 2 t} \cdot \frac{d}{d t}(\cos ^{3} t)-\cos ^{3} t \cdot \frac{d}{d t}(\sqrt{\cos 2 t})}{\cos 2 t} \\ & =\frac{\sqrt{\cos 2 t} \cdot 3 \cos ^{2} t \cdot \frac{d}{d t}(\cos t)-\cos ^{3} t \cdot \frac{1}{2 \sqrt{\cos 2 t}} \cdot \frac{d}{d t}(\cos 2 t)}{\cos 2 t} \\ & =\frac{3 \sqrt{\cos 2 t} \cdot \cos ^{2} t(-\sin t)-\cos ^{3} t \cdot \frac{1}{2 \sqrt{\cos 2 t}} \cdot(-2 \sin 2 t)}{\cos 2 t} \\ & =\frac{-3 \cos 2 t \cdot \cos ^{2} t \cdot \sin t+\cos ^{3} t \sin 2 t}{\cos 2 t \cdot \sqrt{\cos 2 t}} \end{aligned} $
$ \begin{matrix} \therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})} & =\frac{-3 \cos 2 t \cdot \cos ^{2} t \cdot \sin t+\cos ^{3} t \sin 2 t}{3 \cos 2 t \sin ^{2} t \cos t+\sin ^{3} t \sin 2 t} & \\ & =\frac{-3 \cos 2 t \cdot \cos ^{2} t \cdot \sin t+\cos ^{3} t(2 \sin t \cos t)}{3 \cos 2 t \sin ^{2} t \cos t+\sin ^{3} t(2 \sin t \cos t)} & \\ & =\frac{\sin t \cos t[-3 \cos 2 t \cdot \cos t+2 \cos ^{3} t]}{\sin t \cos t[3 \cos 2 t \sin t+2 \sin ^{3} t]} & { \begin{bmatrix} \cos 2 t=(2 \cos ^{2} t-1), \\ \cos 2 t=(1-2 \sin ^{2} t) \end{bmatrix} } \\ & =\frac{[-3(2 \cos { }^{2} t-1) \cos t+2 \cos ^{3} t]}{[3(1-2 \sin ^{2} t) \sin t+2 \sin ^{3} t]} & { \begin{bmatrix} \cos 3 t=4 \cos ^{3} t-3 \cos ^{3} t \\ \sin 3 t=3 \sin ^{3} t-4 \sin ^{3} t \end{bmatrix} } \\ & =\frac{-4 \cos t+3 \cos t}{3 \sin t-4 \sin ^{3} t} & \end{matrix} $
8. $x=a(\cos t+\log \tan \frac{t}{2}) y=a \sin t \quad$
Show Answer
Solution
The given equations are $x=a(\cos t+\log \tan \frac{t}{2})$ and $y=a \sin t$
$ \begin{aligned} & \text{ Then, } \frac{d x}{d t}=a \cdot[\frac{d}{d t}(\cos t)+\frac{d}{d t}(\log \tan \frac{t}{2})] \\ & =a[-\sin t+\frac{1}{\tan \frac{t}{2}} \cdot \frac{d}{d t}(\tan \frac{t}{2})] \\ & =a[-\sin t+\cot \frac{t}{2} \cdot \sec ^{2} \frac{t}{2} \cdot \frac{d}{d t}(\frac{t}{2})] \\ & =a[-\sin t+\frac{\cos \frac{t}{2}}{\sin \frac{t}{2}} \times \frac{1}{\cos ^{2} \frac{t}{2}} \times \frac{1}{2}] \\ & =a[-\sin t+\frac{1}{2 \sin \frac{t}{2} \cos \frac{t}{2}}] \\ & =a(-\sin t+\frac{1}{\sin t}) \\ & =a(\frac{-\sin ^{2} t+1}{\sin t}) \\ & =a \frac{\cos ^{2} t}{\sin t} \\ & \frac{d y}{d t}=a \frac{d}{d t}(\sin t)=a \cos t \\ & \therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{a \cos t}{(a \frac{\cos ^{2} t}{\sin t})}=\frac{\sin t}{\cos t}=\tan t \end{aligned} $
9. $x=a \sec \theta, y=b \tan \theta$
Show Answer
Solution
The given equations are $x=a \sec \theta$ and $y=b \tan \theta$
Then, $\frac{d x}{d \theta}=a \cdot \frac{d}{d \theta}(\sec \theta)=a \sec \theta \tan \theta$
$\frac{d y}{d \theta}=b \cdot \frac{d}{d \theta}(\tan \theta)=b \sec ^{2} \theta$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d \theta})}{(\frac{d x}{d \theta})}=\frac{b \sec ^{2} \theta}{a \sec \theta \tan \theta}=\frac{b}{a} \sec \theta \cot \theta=\frac{b \cos \theta}{a \cos \theta \sin \theta}=\frac{b}{a} \times \frac{1}{\sin \theta}=\frac{b}{a} cosec \theta$
10. $x=a(\cos \theta+\theta \sin \theta), y=a(\sin \theta-\theta \cos \theta)$
Show Answer
Solution
The given equations are $x=a(\cos \theta+\theta \sin \theta)$ and $y=a(\sin \theta-\theta \cos \theta)$
Then, $\frac{d x}{d \theta}=a[\frac{d}{d \theta} \cos \theta+\frac{d}{d \theta}(\theta \sin \theta)]=a[-\sin \theta+\theta \frac{d}{d \theta}(\sin \theta)+\sin \theta \frac{d}{d \theta}(\theta)]$ $=a[-\sin \theta+\theta \cos \theta+\sin \theta]=a \theta \cos \theta$
$ \begin{aligned} \frac{d y}{d \theta}=a[\frac{d}{d \theta}(\sin \theta)-\frac{d}{d \theta}(\theta \cos \theta)] & =a[\cos \theta-{\theta \frac{d}{d \theta}(\cos \theta)+\cos \theta \cdot \frac{d}{d \theta}(\theta)}] \\ & =a[\cos \theta+\theta \sin \theta-\cos \theta] \\ & =a \theta \sin \theta \end{aligned} $
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d \theta})}{(\frac{d x}{d \theta})}=\frac{a \theta \sin \theta}{a \theta \cos \theta}=\tan \theta$
11. If $x=\sqrt{a^{\sin ^{-1} t}}, y=\sqrt{a^{\cos ^{-1} t}}$, show that $\frac{d y}{d x}=-\frac{y}{x}$
Show Answer
Solution
The given equations are $x=\sqrt{a^{\sin ^{-1} t}}$ and $y=\sqrt{a^{\cos ^{-1} t}}$
$x=\sqrt{a^{\sin ^{-1} t}}$ and $y=\sqrt{a^{\cos ^{-1} t}}$
$\Rightarrow x=(a^{\sin ^{-1} t})^{\frac{1}{2}}$ and $y=(a^{\cos ^{-1} t})^{\frac{1}{2}}$
$\Rightarrow x=a^{\frac{1}{2} \sin ^{-1} t}$ and $y=a^{\frac{1}{2} \cos ^{-1} t}$
Consider $x=a^{\frac{1}{2} \sin ^{-1} t}$
Taking logarithm on both the sides, we obtain
$\log x=\frac{1}{2} \sin ^{-1} t \log a$
$\therefore \frac{1}{x} \cdot \frac{d x}{d t}=\frac{1}{2} \log a \cdot \frac{d}{d t}(\sin ^{-1} t)$
$\Rightarrow \frac{d x}{d t}=\frac{x}{2} \log a \cdot \frac{1}{\sqrt{1-t^{2}}}$
$\Rightarrow \frac{d x}{d t}=\frac{x \log a}{2 \sqrt{1-t^{2}}}$
Then, consider $y=a^{\frac{1}{2} \cos ^{-1} t}$
Taking logarithm on both the sides, we obtain
$\log y=\frac{1}{2} \cos ^{-1} t \log a$
$\therefore \frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2} \log a \cdot \frac{d}{d t}(\cos ^{-1} t)$
$\Rightarrow \frac{d y}{d t}=\frac{y \log a}{2} \cdot(\frac{-1}{\sqrt{1-t^{2}}})$
$\Rightarrow \frac{d y}{d t}=\frac{-y \log a}{2 \sqrt{1-t^{2}}}$ $\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{(\frac{-y \log a}{2 \sqrt{1-t^{2}}})}{(\frac{x \log a}{2 \sqrt{1-t^{2}}})}=-\frac{y}{x}$.
Hence, proved.
5.7 Second Order Derivative
$$ \begin{align*} \text {Let} \qquad y & =f(x) \text {. Then } \\ \frac{d y}{d x} & =f^{\prime}(x) \tag{1} \end{align*} $$
If $f^{\prime}(x)$ is differentiable, we may differentiate (1) again w.r.t. $x$. Then, the left hand side becomes $\frac{d}{d x}(\frac{d y}{d x})$ which is called the second order derivative of $y$ w.r.t. $x$ and is denoted by $\frac{d^{2} y}{d x^{2}}$. The second order derivative of $f(x)$ is denoted by $f^{\prime \prime}(x)$. It is also denoted by $D^{2} y$ or $y^{\prime \prime}$ or $y_2$ if $y=f(x)$. We remark that higher order derivatives may be defined similarly.
Example 34 Find $\frac{d^{2} y}{d x^{2}}$, if $y=x^{3}+\tan x$.
Solution Given that $y=x^{3}+\tan x$. Then
Therefore $\qquad \begin{aligned}\frac{d y}{d x} & =3 x^{2}+\sec ^{2} x \\ \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}\left(3 x^{2}+\sec ^{2} x\right) \\ & =6 x+2 \sec x \cdot \sec x \tan x=6 x+2 \sec ^{2} x \tan x\end{aligned}$
Example 35 If $y=A \sin x+B \cos x$, then prove that $\frac{d^{2} y}{d x^{2}}+y=0$.
Solution We have
$$ \begin{aligned} & \frac{d y}{d x}=\mathrm{A} \cos x-\mathrm{B} \sin x \\ \text{ and } \qquad & \frac{d^2 y}{d x^2} =\frac{d}{d x}(\mathrm{~A} \cos x-\mathrm{B} \sin x) \\ & \qquad =-\mathrm{A} \sin x-\mathrm{B} \cos x=-y \\ \text{ Hence } \qquad & \frac{d^2 y}{d x^2}+y=0 \end{aligned} $$
Example 36 If $y=3 e^{2 x}+2 e^{3 x}$, prove that $\frac{d^{2} y}{d x^{2}}-5 \frac{d y}{d x}+6 y=0$.
Solution Given that $y=3 e^{2 x}+2 e^{3 x}$.
Then $\qquad \frac{d y}{d x}=6 e^{2 x}+6 e^{3 x}=6\left(e^{2 x}+e^{3 x}\right)$
Therefore $\qquad \frac{d^{2} y}{d x^{2}}=12 e^{2 x}+18 e^{3 x}=6\left(2 e^{2 x}+3 e^{3 x}\right)$
$$ \frac{d^{2} y}{d x^{2}}-5 \frac{d y}{d x}+6 y=6\left(2 e^{2 x}+3 e^{3 x}\right) $$
$$ -30\left(e^{2 x}+e^{3 x}\right)+6\left(3 e^{2 x}+2 e^{3 x}\right)=0 $$
Example 37 If $y=\sin ^{-1} x$, show that $(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=0$.
Solution We have $y=\sin ^{-1} x$.
Then $\qquad \frac{d y}{d x}=\frac{1}{\sqrt{\left(1-x^{2}\right)}}$
$$ \sqrt{\left(1-x^{2}\right)} \frac{d y}{d x}=1 $$
or $\qquad \frac{d}{d x}\left(\sqrt{\left(1-x^{2}\right)} \cdot \frac{d y}{d x}\right)=0$
or $\qquad\sqrt{\left(1-x^{2}\right)} \cdot \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot \frac{d}{d x}\left(\sqrt{\left(1-x^{2}\right)}\right)=0$
$ \begin{aligned}\text {or } \qquad & \sqrt{\left(1-x^{2}\right)} \cdot \frac{d^{2} y}{d x{2}}-\frac{d y}{d x} \cdot \frac{2 x}{2 \sqrt{1-x^{2}}}=0 \\ & \left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=0\end{aligned}$
Alternatively, Given that $y=\sin ^{-1} x$, we have
$$ y_1=\frac{1}{\sqrt{1-x^{2}}} \text{, i.e., }(1-x^{2}) y_1^{2}=1 $$
So $\qquad (1-x^{2}) \cdot 2 y_1 y_2+y_1^{2}(0-2 x)=0$
Hence $\qquad \left(1-x^{2}\right) y _{2}-x y _{1}=0$
EXERCISE 5.7
Find the second order derivatives of the functions given in Exercises 1 to 10.
1. $x^{2}+3 x+2$
Show Answer
Solution
Let $y=x^{2}+3 x+2$
Then,
$\frac{d y}{d x}=\frac{d}{d x}(x^{2})+\frac{d}{d x}(3 x)+\frac{d}{d x}(2)=2 x+3+0=2 x+3$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(2 x+3)=\frac{d}{d x}(2 x)+\frac{d}{d x}(3)=2+0=2$
2. $x^{20}$
Show Answer
Solution
Let $y=x^{20}$
Then,
$\frac{d y}{d x}=\frac{d}{d x}(x^{20})=20 x^{19}$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(20 x^{19})=20 \frac{d}{d x}(x^{19})=20 \cdot 19 \cdot x^{18}=380 x^{18}$
3. $x \cdot \cos x$
Show Answer
Solution
Let $y=x \cdot \cos x$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(x \cdot \cos x)=\cos x \cdot \frac{d}{d x}(x)+x \frac{d}{d x}(\cos x)=\cos x \cdot 1+x(-\sin x)=\cos x-x \sin x \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[\cos x-x \sin x]=\frac{d}{d x}(\cos x)-\frac{d}{d x}(x \sin x) \\ & =-\sin x-[\sin x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\sin x)] \\ & =-\sin x-(\sin x+x \cos x) \\ & =-(x \cos x+2 \sin x) \end{aligned} \end{aligned} $
4. $\log x$
Show Answer
Solution
Let $y=\log x$
Then,
$\frac{d y}{d x}=\frac{d}{d x}(\log x)=\frac{1}{x}$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(\frac{1}{x})=\frac{-1}{x^{2}}$
5. $x^{3} \log x$
Show Answer
Solution
Let $y=x^{3} \log x$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[x^{3} \log x]=\log x \cdot \frac{d}{d x}(x^{3})+x^{3} \cdot \frac{d}{d x}(\log x) \\ & =\log x \cdot 3 x^{2}+x^{3} \cdot \frac{1}{x}=\log x \cdot 3 x^{2}+x^{2} \\ & =x^{2}(1+3 \log x) \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[x^{2}(1+3 \log x)] \\ & =(1+3 \log x) \cdot \frac{d}{d x}(x^{2})+x^{2} \frac{d}{d x}(1+3 \log x) \\ & =(1+3 \log x) \cdot 2 x+x^{2} \cdot \frac{3}{x} \\ & =2 x+6 x \log x+3 x \\ & =5 x+6 x \log x \\ & =x(5+6 \log x) \end{aligned} $
6. $e^{x} \sin 5 x$
Show Answer
Solution
Let $y=e^{x} \sin 5 x$
Then,
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}(e^{x} \sin 5 x)=\sin 5 x \cdot \frac{d}{d x}(e^{x})+e^{x} \frac{d}{d x}(\sin 5 x) \\ & =\sin 5 x \cdot e^{x}+e^{x} \cdot \cos 5 x \cdot \frac{d}{d x}(5 x)=e^{x} \sin 5 x+e^{x} \cos 5 x \cdot 5 \\ & =e^{x}(\sin 5 x+5 \cos 5 x) \\ \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[e^{x}(\sin 5 x+5 \cos 5 x)] \\ & =(\sin 5 x+5 \cos 5 x) \cdot \frac{d}{d x}(e^{x})+e^{x} \cdot \frac{d}{d x}(\sin 5 x+5 \cos 5 x) \\ & =(\sin 5 x+5 \cos 5 x) e^{x}+e^{x}[\cos 5 x \cdot \frac{d}{d x}(5 x)+5(-\sin 5 x) \cdot \frac{d}{d x}(5 x)] \\ & =e^{x}(\sin 5 x+5 \cos 5 x)+e^{x}(5 \cos 5 x-25 \sin 5 x) \\ & =e^{x}(10 \cos 5 x-24 \sin 5 x)=2 e^{x}(5 \cos 5 x-12 \sin 5 x) \end{aligned} $
7. $e^{6 x} \cos 3 x$
Show Answer
Solution
Let $y=e^{6 x} \cos 3 x$
Then,
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}(e^{6 x} \cdot \cos 3 x)=\cos 3 x \cdot \frac{d}{d x}(e^{6 x})+e^{6 x} \cdot \frac{d}{d x}(\cos 3 x) \\ & =\cos 3 x \cdot e^{6 x} \cdot \frac{d}{d x}(6 x)+e^{6 x} \cdot(-\sin 3 x) \cdot \frac{d}{d x}(3 x) \\ & =6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x \\ \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}(6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x)=6 \cdot \frac{d}{d x}(e^{6 x} \cos 3 x)-3 \cdot \frac{d}{d x}(e^{6 x} \sin 3 x) \\ & =6 \cdot[6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x]-3 \cdot[\sin 3 x \cdot \frac{d}{d x}(e^{6 x})+e^{6 x} \cdot \frac{d}{d x}(\sin 3 x)] \\ & =36 e^{6 x} \cos 3 x-18 e^{6 x} \sin 3 x-3[\sin 3 x \cdot e^{6 x} \cdot 6+e^{6 x} \cdot \cos 3 x \cdot 3] \\ & =36 e^{6 x} \cos 3 x-18 e^{6 x} \sin 3 x-18 e^{6 x} \sin 3 x-9 e^{6 x} \cos 3 x \\ & =27 e^{6 x} \cos 3 x-36 e^{6 x} \sin 3 x \\ & =9 e^{6 x}(3 \cos 3 x-4 \sin 3 x) \end{aligned} $
8. $\tan ^{-1} x$
Show Answer
Solution
Let $y=\tan ^{-1} x$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(\tan ^{-1} x)=\frac{1}{1+x^{2}} \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(\frac{1}{1+x^{2}})=\frac{d}{d x}(1+x^{2})^{-1}=(-1) \cdot(1+x^{2})^{-2} \cdot \frac{d}{d x}(1+x^{2}) \\ & \quad=\frac{-1}{(1+x^{2})^{2}} \times 2 x=\frac{-2 x}{(1+x^{2})^{2}} \end{aligned} $
9. $\log (\log x)$
Show Answer
Solution
Let $y=\log (\log x)$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[\log (\log x)]=\frac{1}{\log x} \cdot \frac{d}{d x}(\log x)=\frac{1}{x \log x}=(x \log x)^{-1} \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[(x \log x)^{-1}]=(-1) \cdot(x \log x)^{-2} \cdot \frac{d}{d x}(x \log x) \\ & =\frac{-1}{(x \log x)^{2}} \cdot[\log x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log x)] \\ & =\frac{-1}{(x \log x)^{2}} \cdot[\log x \cdot 1+x \cdot \frac{1}{x}]=\frac{-(1+\log x)}{(x \log x)^{2}} \end{aligned} \end{aligned} $
10. $\sin (\log x)$
Show Answer
Solution
Let $y=\sin (\log x)$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[\sin (\log x)]=\cos (\log x) \cdot \frac{d}{d x}(\log x)=\frac{\cos (\log x)}{x} \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[\frac{\cos (\log x)}{x}] \\ & =\frac{x \cdot \frac{d}{d x}[\cos (\log x)]-\cos (\log x) \cdot \frac{d}{d x}(x)}{x^{2}} \\ & =\frac{x \cdot[-\sin (\log x) \cdot \frac{d}{d x}(\log x)]-\cos (\log x) \cdot 1}{x^{2}} \\ & =\frac{-x \sin (\log x) \cdot \frac{1}{x}-\cos (\log x)}{x^{2}} \\ & =\frac{-[\sin (\log x)+\cos (\log x)]}{x^{2}} \end{aligned} \end{aligned} $
11. If $y=5 \cos x-3 \sin x$, prove that $\frac{d^{2} y}{d x^{2}}+y=0$
Show Answer
Solution
It is given that, $y=5 \cos x-3 \sin x$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(5 \cos x)-\frac{d}{d x}(3 \sin x)=5 \frac{d}{d x}(\cos x)-3 \frac{d}{d x}(\sin x) \\ & =5(-\sin x)-3 \cos x=-(5 \sin x+3 \cos x) \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[-(5 \sin x+3 \cos x)] \\ & =-[5 \cdot \frac{d}{d x}(\sin x)+3 \cdot \frac{d}{d x}(\cos x)] \\ & =-[5 \cos x+3(-\sin x)] \\ & =-[5 \cos x-3 \sin x] \\ & =-y \\ & \therefore \frac{d^{2} y}{d x^{2}}+y=0 \end{aligned} $
Hence, proved.
12. If $y=\cos ^{-1} x$, Find $\frac{d^{2} y}{d x^{2}}$ in terms of $y$ alone.
Show Answer
Solution
It is given that, $y=\cos ^{-1} x$
Then,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(\cos ^{-1} x)=\frac{-1}{\sqrt{1-x^{2}}}=-(1-x^{2})^{\frac{-1}{2}} \\ & \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[-(1-x^{2})^{\frac{-1}{2}}] \\ & =-(-\frac{1}{2}) \cdot(1-x^{2})^{\frac{-3}{2}} \cdot \frac{d}{d x}(1-x^{2}) \\ & =\frac{1}{2 \sqrt{(1-x^{2})^{3}}} \times(-2 x) \\ & \Rightarrow \frac{d^{2} y}{d x^{2}}=\frac{-x}{\sqrt{(1-x^{2})^{3}}} \end{aligned} $
Putting $x=\cos y$ in equation (i), we obtain
$\frac{d^{2} y}{d x^{2}}=\frac{-\cos y}{\sqrt{(1-\cos ^{2} y)^{3}}}$ $\Rightarrow \frac{d^{2} y}{d x^{2}}=\frac{-\cos y}{\sqrt{(\sin ^{2} y)^{3}}}$
$ =\frac{-\cos y}{\sin ^{3} y} $
$ =\frac{-\cos y}{\sin y} \times \frac{1}{\sin ^{2} y} $
$\Rightarrow \frac{d^{2} y}{d x^{2}}=-\cot y \cdot cosec^{2} y$
13. If $y=3 \cos (\log x)+4 \sin (\log x)$, show that $x^{2} y_2+x y_1+y=0$
Show Answer
Solution
It is given that, $y=3 \cos (\log x)+4 \sin (\log x)$
Then,
$ \begin{aligned} & y_1=3 \cdot \frac{d}{d x}[\cos (\log x)]+4 \cdot \frac{d}{d x}[\sin (\log x)] \\ & =3 \cdot[-\sin (\log x) \cdot \frac{d}{d x}(\log x)]+4 \cdot[\cos (\log x) \cdot \frac{d}{d x}(\log x)] \\ & \therefore y_1=\frac{-3 \sin (\log x)}{x}+\frac{4 \cos (\log x)}{x}=\frac{4 \cos (\log x)-3 \sin (\log x)}{x} \\ & \therefore y_2=\frac{d}{d x}(\frac{4 \cos (\log x)-3 \sin (\log x)}{x}) \\ & =\frac{x{4 \cos (\log x)-3 \sin (\log x)}^{\prime}-{4 \cos (\log x)-3 \sin (\log x)}(x)^{\prime}}{x^{2}} \\ & =\frac{x[4{\cos (\log x)}^{\prime}-3{\sin (\log x)}^{\prime}]-{4 \cos (\log x)-3 \sin (\log x)} \cdot 1}{x^{2}} \\ & =\frac{x[-4 \sin (\log x) \cdot(\log x)^{\prime}-3 \cos (\log x) \cdot(\log x)^{\prime}]-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{x[-4 \sin (\log x) \cdot \frac{1}{x}-3 \cos (\log x) \cdot \frac{1}{x}]-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{-4 \sin (\log x)-3 \cos (\log x)-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{-\sin (\log x)-7 \cos (\log x)}{x^{2}} \\ & \therefore x^{2} y_2+x y_1+y \\ & =x^{2}(\frac{-\sin (\log x)-7 \cos (\log x)}{x^{2}})+x(\frac{4 \cos (\log x)-3 \sin (\log x)}{x})+3 \cos (\log x)+4 \sin (\log x) \\ & =-\sin (\log x)-7 \cos (\log x)+4 \cos (\log x)-3 \sin (\log x)+3 \cos (\log x)+4 \sin (\log x) \\ & =0 \end{aligned} $
Hence, proved.
14. If $y=A e^{m x}+B e^{n x}$, show that $\frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y=0$
Show Answer
Solution
It is given that, $y=A e^{m x}+B e^{n x}$
Then,
$ \begin{aligned} & \frac{d y}{d x}=A \cdot \frac{d}{d x}(e^{m x})+B \cdot \frac{d}{d x}(e^{n x})=A \cdot e^{m x} \cdot \frac{d}{d x}(m x)+B \cdot e^{n x} \cdot \frac{d}{d x}(n x)=A m e^{n x x}+B n e^{n x} \\ & \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(A m e^{m x}+B n e^{n x})=A m \cdot \frac{d}{d x}(e^{m x})+B n \cdot \frac{d}{d x}(e^{n x}) \\ & =A m \cdot e^{m x} \cdot \frac{d}{d x}(m x)+B n \cdot e^{n x} \cdot \frac{d}{d x}(n x)=A m^{2} e^{m x}+B n^{2} e^{n x} \\ & \therefore \frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y \\ & =A m^{2} e^{m x}+B n^{2} e^{n x}-(m+n) \cdot(A m e^{m x}+B n e^{n x})+m n(A e^{m x}+B e^{n x}) \\ & =A m^{2} e^{n x x}+B n^{2} e^{n x}-A m^{2} e^{n x x}-B m n e^{n x}-A m n e^{m x x}-B n^{2} e^{n x}+A m n e^{n x x}+B m n e^{n x} \\ & =0 \end{aligned} $
Hence, proved.
15. If $y=500 e^{7 x}+600 e^{-7 x}$, show that $\frac{d^{2} y}{d x^{2}}=49 y$
Show Answer
Solution
It is given that, $y=500 e^{7 x}+600 e^{-7 x}$
Then,
$ \begin{aligned} \frac{d y}{d x} & =500 \cdot \frac{d}{d x}(e^{7 x})+600 \cdot \frac{d}{d x}(e^{-7 x}) \\ & =500 \cdot e^{7 x} \cdot \frac{d}{d x}(7 x)+600 \cdot e^{-7 x} \cdot \frac{d}{d x}(-7 x) \\ & =3500 e^{7 x}-4200 e^{-7 x} \\ \therefore \frac{d^{2} y}{d x^{2}} & =3500 \cdot \frac{d}{d x}(e^{7 x})-4200 \cdot \frac{d}{d x}(e^{-7 x}) \\ & =3500 \cdot e^{7 x} \cdot \frac{d}{d x}(7 x)-4200 \cdot e^{-7 x} \cdot \frac{d}{d x}(-7 x) \\ & =7 \times 3500 \cdot e^{7 x}+7 \times 4200 \cdot e^{-7 x} \\ & =49 \times 500 e^{7 x}+49 \times 600 e^{-7 x} \\ & =49(500 e^{7 x}+600 e^{-7 x}) \\ & =49 y \end{aligned} $
Hence, proved.
16. If $e^{y}(x+1)=1$, show that $\frac{d^{2} y}{d x^{2}}=(\frac{d y}{d x})^{2}$
Show Answer
Solution
The given relationship is $e^{y}(x+1)=1$
$e^{y}(x+1)=1$
$\Rightarrow e^{y}=\frac{1}{x+1}$
Taking logarithm on both the sides, we obtain
$y=\log \frac{1}{(x+1)}$
Differentiating this relationship with respect to $x$, we obtain $\frac{d y}{d x}=(x+1) \frac{d}{d x}(\frac{1}{x+1})=(x+1) \cdot \frac{-1}{(x+1)^{2}}=\frac{-1}{x+1}$
$\therefore \frac{d^{2} y}{d x^{2}}=-\frac{d}{d x}(\frac{1}{x+1})=-(\frac{-1}{(x+1)^{2}})=\frac{1}{(x+1)^{2}}$
$\Rightarrow \frac{d^{2} y}{d x^{2}}=(\frac{-1}{x+1})^{2}$
$\Rightarrow \frac{d^{2} y}{d x^{2}}=(\frac{d y}{d x})^{2}$
Hence, proved.
17. If $y=(\tan ^{-1} x)^{2}$, show that $(x^{2}+1)^{2} y_2+2 x(x^{2}+1) y_1=2$
Show Answer
Solution
The given relationship is $y=(\tan ^{-1} x)^{2}$
Then,
$y _1=2 \tan ^{-1} x \frac{d}{d x}(\tan ^{-1} x)$
$\Rightarrow y _1=2 \tan ^{-1} x \cdot \frac{1}{1+x^{2}}$
$\Rightarrow(1+x^{2}) y _1=2 \tan^{-1} x$
Again differentiating with respect to $x$ on both the sides, we obtain
$(1+x^{2}) y _2+2 x y _1=2(\frac{1}{1+x^{2}})$
$\Rightarrow(1+x^{2})^{2} y _2+2 x(1+x^{2}) y _1=2$
Hence, proved.
Miscellaneous Examples
Example 39 Differentiate w.r.t. $x$, the following function:
(i) $\sqrt{3 x+2}+\frac{1}{\sqrt{2 x^{2}+4}}$
(ii) $\log _7(\log x)$
Solution
(i) Let $y=\sqrt{3 x+2}+\frac{1}{\sqrt{2 x^{2}+4}}=(3 x+2)^{\frac{1}{2}}+(2 x^{2}+4)^{-\frac{1}{2}}$
Note that this function is defined at all real numbers $x>-\frac{2}{3}$. Therefore
$$ \begin{aligned} \frac{d y}{d x} & =\frac{1}{2}(3 x+2)^{\frac{1}{2}-1} \cdot \frac{d}{d x}(3 x+2)+(-\frac{1}{2})(2 x^{2}+4)^{-\frac{1}{2}-1} \cdot \frac{d}{d x}(2 x^{2}+4) \\ & =\frac{1}{2}(3 x+2)^{-\frac{1}{2}} \cdot(3)-\frac{1}{2}(2 x^{2}+4)^{-\frac{3}{2}} \cdot 4 x \\ & =\frac{3}{2 \sqrt{3 x+2}}-\frac{2 x}{(2 x^{2}+4)^{\frac{3}{2}}} \end{aligned} $$
This is defined for all real numbers $x>-\frac{2}{3}$. (ii) Let $y=\log _7(\log x)=\frac{\log (\log x)}{\log 7}$ (by change of base formula).
The function is defined for all real numbers $x>1$. Therefore
$$ \begin{aligned} \frac{d y}{d x} & =\frac{1}{\log 7} \frac{d}{d x}(\log (\log x)) \\ & =\frac{1}{\log 7} \frac{1}{\log x} \cdot \frac{d}{d x}(\log x) \\ & =\frac{1}{x \log 7 \log x} \end{aligned} $$
Example 40 Differentiate the following w.r.t. $x$.
(i) $\cos ^{-1}(\sin x)$
(ii) $\tan ^{-1}(\frac{\sin x}{1+\cos x})$
(iii) $\sin ^{-1}(\frac{2^{x+1}}{1+4^{x}})$
Solution
(i) Let $f(x)=\cos ^{-1}(\sin x)$. Observe that this function is defined for all real numbers. We may rewrite this function as
$$ \begin{aligned} f(x) & =\cos ^{-1}(\sin x) \\ & =\cos ^{-1} \cos \frac{\pi}{2}-x \\ & =\frac{\pi}{2}-x \end{aligned} $$
Thus $$ f^{\prime}(x)=-1 \text{. } $$
(ii) Let $f(x)=\tan ^{-1}(\frac{\sin x}{1+\cos x})$. Observe that this function is defined for all real numbers, where $\cos x \neq-1$; i.e., at all odd multiplies of $\pi$. We may rewrite this function as
$$ \begin{aligned} f(x) & =\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right) \\ & =\tan ^{-1}\left[\frac{2 \sin \left(\frac{x}{2}\right) \cos \left(\frac{x}{2}\right)}{2 \cos ^{2} \frac{x}{2}}\right] \\ & =\tan ^{-1}\left[\tan \left(\frac{x}{2}\right)\right]=\frac{x}{2} \end{aligned} $$
Observe that we could cancel $\cos (\frac{x}{2})$ in both numerator and denominator as it is not equal to zero. Thus $f^{\prime}(x)=\frac{1}{2}$.
(iii) Let $f(x)=\sin ^{-1}(\frac{2^{x+1}}{1+4^{x}})$. To find the domain of this function we need to find all $x$ such that $-1 \leq \frac{2^{x+1}}{1+4^{x}} \leq 1$. Since the quantity in the middle is always positive, we need to find all $x$ such that $\frac{2^{x+1}}{1+4^{x}} \leq 1$, i.e., all $x$ such that $2^{x+1} \leq 1+4^{x}$. We may rewrite this as $2 \leq \frac{1}{2^{x}}+2^{x}$ which is true for all $x$. Hence the function is defined at every real number. By putting $2^{x}=\tan \theta$, this function may be rewritten as
$ \begin{aligned} f(x) & =\sin ^{-1}[\frac{2^{x+1}}{1+4^{x}}] \\ & =\sin ^{-1} \frac{2^{x} \cdot 2}{1+(2^{x})^{2}} \\ & =\sin ^{-1}[\frac{2 \tan \theta}{1+\tan ^{2} \theta}] \\ & =\sin ^{-1}[\sin 2 \theta] \\ & =2 \theta=2 \tan ^{-1}(2^{x}) \end{aligned} $
Thus $$ \begin{aligned} f^{\prime}(x) & =2 \cdot \frac{1}{1+(2^{x})^{2}} \cdot \frac{d}{d x}(2^{x}) \\ & =\frac{2}{1+4^{x}} \cdot(2^{x}) \log 2 \\ & =\frac{2^{x+1} \log 2}{1+4^{x}} \end{aligned} $$
Example 41 Find $f^{\prime}(x)$ if $f(x)=(\sin x)^{\sin x}$ for all $0<x<\pi$.
Solution The function $y=(\sin x)^{\sin x}$ is defined for all positive real numbers. Taking logarithms, we have
Then $$ \begin{aligned} \log y & =\log (\sin x)^{\sin x}=\sin x \log (\sin x) \\ \frac{1}{y} \frac{d y}{d x} & =\frac{d}{d x}(\sin x \log (\sin x)) \\ & =\cos x \log (\sin x)+\sin x \cdot \frac{1}{\sin x} \cdot \frac{d}{d x}(\sin x) \\ & =\cos x \log (\sin x)+\cos x \\ & =(1+\log (\sin x)) \cos x \end{aligned} $$
Thus $ \frac{d y}{d x}=y((1+\log (\sin x)) \cos x)=(1+\log (\sin x))(\sin x)^{\sin x} \cos x $
Example 42 For a positive constant $a$ find $\frac{d y}{d x}$, where
$$ y=a^{t+\frac{1}{t}}, \text{ and } x=(t+\frac{1}{t})^{a} $$
Solution Observe that both $y$ and $x$ are defined for all real $t \neq 0$. Clearly
$$ \begin{aligned} \frac{d y}{d t}=\frac{d}{d t}\left(a^{t+\frac{1}{t}}\right) & =a^{t+\frac{1}{t}} \frac{d}{d t}\left(t+\frac{1}{t}\right) \cdot \log a \\ & =a^{t+\frac{1}{t}}\left(1-\frac{1}{t^{2}}\right) \log a \\ \frac{d x}{d t} & =a\left[t+\frac{1}{t}\right]^{a-1} \cdot \frac{d}{d t}\left(t+\frac{1}{t}\right) \\ & =a\left[t+\frac{1}{t}\right]^{a-1} \cdot\left(1-\frac{1}{t^{2}}\right) \\ \frac{d x}{d t} & \neq 0 \text { only if } t \neq \pm 1 \text { Thus for } t \neq \pm 1 \\ \frac{d y}{d x}=\frac{d y}{\frac{d x}{d t}} & =\frac{a^{t+\frac{1}{t}}\left(1-\frac{1}{t^{2}}\right) \log a}{\left.a^{\left[t+\frac{1}{t}\right.}\right]^{a-1} \cdot\left(1-\frac{1}{t^{2}}\right)}=\frac{a^{t+\frac{1}{t}} \log a}{a\left(t+\frac{1}{t}\right)^{a-1}} \end{aligned} $$
Example 43 Differentiate $\sin ^{2} x$ w.r.t. $e^{\cos x}$.
Solution Let $u(x)=\sin ^{2} x$ and $v(x)=e^{\cos x}$. We want to find $\frac{d u}{d v}=\frac{d u / d x}{d v / d x}$. Clearly
$$ \frac{d u}{d x}=2 \sin x \cos x \text{ and } \frac{d v}{d x}=e^{\cos x}(-\sin x)=-(\sin x) e^{\cos x} $$ Thus $$ \frac{d u}{d v}=\frac{2 \sin x \cos x}{-\sin x e^{\cos x}}=-\frac{2 \cos x}{e^{\cos x}} $$
Miscellaneous Exercise on Chapter 5
Differentiate w.r.t. $x$ the function in Exercises 1 to 11 .
1. $(3 x^{2}-9 x+5)^{9}$
Show Answer
Solution
Let $y=(3 x^{2}-9 x+5)^{9}$
Using chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}(3 x^{2}-9 x+5)^{9} \\ & =9(3 x^{2}-9 x+5)^{8} \cdot \frac{d}{d x}(3 x^{2}-9 x+5) \\ & =9(3 x^{2}-9 x+5)^{8} \cdot(6 x-9) \\ & =9(3 x^{2}-9 x+5)^{8} \cdot 3(2 x-3) \\ & =27(3 x^{2}-9 x+5)^{8}(2 x-3) \end{aligned} $
2. $\sin ^{3} x+\cos ^{6} x$
Show Answer
Solution
$ \begin{aligned} & \text{ Let } y=\sin ^{3} x+\cos ^{6} x \\ & \therefore \frac{d y}{d x}=\frac{d}{d x}(\sin ^{3} x)+\frac{d}{d x}(\cos ^{6} x) \\ & =3 \sin ^{2} x \cdot \frac{d}{d x}(\sin x)+6 \cos ^{5} x \cdot \frac{d}{d x}(\cos x) \\ & =3 \sin ^{2} x \cdot \cos x+6 \cos ^{5} x \cdot(-\sin x) \\ & =3 \sin x \cos x(\sin x-2 \cos ^{4} x) \end{aligned} $
3. $(5 x)^{3 \cos 2 x}$
Show Answer
Solution
Let $y=(5 x)^{3 \cos 2 x}$
Taking logarithm on both the sides, we obtain
$\log y=3 \cos 2 x \log 5 x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{y} \frac{d y}{d x}=3[\log 5 x \cdot \frac{d}{d x}(\cos 2 x)+\cos 2 x \cdot \frac{d}{d x}(\log 5 x)]$
$\Rightarrow \frac{d y}{d x}=3 y[\log 5 x(-\sin 2 x) \cdot \frac{d}{d x}(2 x)+\cos 2 x \cdot \frac{1}{5 x} \cdot \frac{d}{d x}(5 x)]$
$\Rightarrow \frac{d y}{d x}=3 y[-2 \sin 2 x \log 5 x+\frac{\cos 2 x}{x}]$
$\Rightarrow \frac{d y}{d x}=3 y[\frac{3 \cos 2 x}{x}-6 \sin 2 x \log 5 x]$
$\therefore \frac{d y}{d x}=(5 x)^{3 \cos 2 x}[\frac{3 \cos 2 x}{x}-6 \sin 2 x \log 5 x]$
4. $\sin ^{-1}(x \sqrt{x}), 0 \leq x \leq 1$
Show Answer
Solution
Let $y=\sin ^{-1}(x \sqrt{x})$
Using chain rule, we obtain
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x} \sin ^{-1}(x \sqrt{x}) \\ & =\frac{1}{\sqrt{1-(x \sqrt{x})^{2}}} \times \frac{d}{d x}(x \sqrt{x}) \\ & =\frac{1}{\sqrt{1-x^{3}}} \cdot \frac{d}{d x}(x^{\frac{3}{2}}) \\ & =\frac{1}{\sqrt{1-x^{3}}} \times \frac{3}{2} \cdot x^{\frac{1}{2}} \\ & =\frac{3 \sqrt{x}}{2 \sqrt{1-x^{3}}} \\ & =\frac{3}{2} \sqrt{\frac{x}{1-x^{3}}} \end{aligned} $
5. $\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}},-2<x<2$
Show Answer
Solution
Let $y=\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}$
By quotient rule, we obtain
$ \begin{aligned} & \frac{d y}{d x}=\frac{\sqrt{2 x+7} \frac{d}{d x}(\cos ^{-1} \frac{x}{2})-(\cos ^{-1} \frac{x}{2}) \frac{d}{d x}(\sqrt{2 x+7})}{(\sqrt{2 x+7})^{2}} \\ & =\frac{\sqrt{2 x+7}[\frac{-1}{\sqrt{1-(\frac{x}{2})^{2}}} \cdot \frac{d}{d x}(\frac{x}{2})]-(\cos ^{-1} \frac{x}{2}) \frac{1}{2 \sqrt{2 x+7}} \cdot \frac{d}{d x}(2 x+7)}{2 x+7} \\ & =\frac{\sqrt{2 x+7} \frac{-1}{\sqrt{4-x^{2}}}-(\cos ^{-1} \frac{x}{2}) \frac{2}{2 \sqrt{2 x+7}}}{2 x+7} \\ & =\frac{-\sqrt{2 x+7}}{\sqrt{4-x^{2}} \times(2 x+7)}-\frac{\cos ^{-1} \frac{x}{2}}{(\sqrt{2 x+7})(2 x+7)} \\ & =-[\frac{1}{\sqrt{4-x^{2}} \sqrt{2 x+7}}+\frac{\cos ^{-1} \frac{x}{2}}{(2 x+7)^{\frac{3}{2}}}] \end{aligned} $
6. $\cot ^{-1}[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}], 0<x<\frac{\pi}{2}$
Show Answer
Solution
Let $y=\cot ^{-1}[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}]$
Then, $\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}$
$=\frac{(\sqrt{1+\sin x}+\sqrt{1-\sin x})^{2}}{(\sqrt{1+\sin x}-\sqrt{1-\sin x})(\sqrt{1+\sin x}+\sqrt{1-\sin x})}$
$=\frac{(1+\sin x)+(1-\sin x)+2 \sqrt{(1-\sin x)(1+\sin x)}}{(1+\sin x)-(1-\sin x)}$
$=\frac{2+2 \sqrt{1-\sin ^{2} x}}{2 \sin x}$
$=\frac{1+\cos x}{\sin x}$
$=\frac{2 \cos ^{2} \frac{x}{2}}{2 \sin \frac{x}{2} \cos \frac{x}{2}}$
$=\cot \frac{x}{2}$
Therefore, equation (1) becomes
$y=\cot ^{-1}(\cot \frac{x}{2})$
$\Rightarrow y=\frac{x}{2}$
$\therefore \frac{d y}{d x}=\frac{1}{2} \frac{d}{d x}(x)$
$\Rightarrow \frac{d y}{d x}=\frac{1}{2}$
7. $(\log x)^{\log x}, x>1$
Show Answer
Solution
Let $y=(\log x)^{\log x}$
Taking logarithm on both the sides, we obtain
$\log y=\log x \cdot \log (\log x)$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{y} \frac{d y}{d x}=\frac{d}{d x}[\log x \cdot \log (\log x)]$
$\Rightarrow \frac{1}{y} \frac{d y}{d x}=\log (\log x) \cdot \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}[\log (\log x)]$
$\Rightarrow \frac{d y}{d x}=y[\log (\log x) \cdot \frac{1}{x}+\log x \cdot \frac{1}{\log x} \cdot \frac{d}{d x}(\log x)]$
$\Rightarrow \frac{d y}{d x}=y[\frac{1}{x} \log (\log x)+\frac{1}{x}]$
$\therefore \frac{d y}{d x}=(\log x)^{\log x}[\frac{1}{x}+\frac{\log (\log x)}{x}]$
8. $\cos (a \cos x+b \sin x)$, for some constant $a$ and $b$.
Show Answer
Solution
Let $y=\cos (a \cos x+b \sin x)$
By using chain rule, we obtain
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x} \cos (a \cos x+b \sin x) \\ & \begin{aligned} \Rightarrow \frac{d y}{d x} & =-\sin (a \cos x+b \sin x) \cdot \frac{d}{d x}(a \cos x+b \sin x) \\ & =-\sin (a \cos x+b \sin x) \cdot[a(-\sin x)+b \cos x] \\ & =(a \sin x-b \cos x) \cdot \sin (a \cos x+b \sin x) \end{aligned} \end{aligned} $
9. $(\sin x-\cos x)^{(\sin x-\cos x)}, \frac{\pi}{4}<x<\frac{3 \pi}{4}$
Show Answer
Solution
Let $y=(\sin x-\cos x)^{(\sin x-\cos x)}$
Taking logarithm on both the sides, we obtain
$\log y=\log [(\sin x-\cos x)^{(\sin x-\cos x)}]$
$\Rightarrow \log y=(\sin x-\cos x) \cdot \log (\sin x-\cos x)$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{y} \frac{d y}{d x}=\frac{d}{d x}[(\sin x-\cos x) \log (\sin x-\cos x)]$
$\Rightarrow \frac{1}{y} \frac{d y}{d x}=\log (\sin x-\cos x) \cdot \frac{d}{d x}(\sin x-\cos x)+(\sin x-\cos x) \cdot \frac{d}{d x} \log (\sin x-\cos x)$
$\Rightarrow \frac{1}{y} \frac{d y}{d x}=\log (\sin x-\cos x) \cdot(\cos x+\sin x)+(\sin x-\cos x) \cdot \frac{1}{(\sin x-\cos x)} \cdot \frac{d}{d x}(\sin x-\cos x)$
$\Rightarrow \frac{d y}{d x}=(\sin x-\cos x)^{(\sin x-\cos x)}[(\cos x+\sin x) \cdot \log (\sin x-\cos x)+(\cos x+\sin x)]$
$\therefore \frac{d y}{d x}=(\sin x-\cos x)^{(\sin x-\cos x)}(\cos x+\sin x)[1+\log (\sin x-\cos x)]$
10. $x^{x}+x^{a}+a^{x}+a^{a}$, for some fixed $a>0$ and $x>0$
Show Answer
Solution
Let $y=x^{x}+x^{a}+a^{x}+a^{a}$
Also, let $x^{x}=u, x^{a}=v, a^{x}=w$, and $a^{a}=s$
$\therefore y=u+v+w+s$
$\Rightarrow \frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}+\frac{d s}{d x}$
$u=x^{x}$
$\Rightarrow \log u=\log x^{x}$
$\Rightarrow \log u=x \log x$
Differentiating both sides with respect to $x$, we obtain $\frac{1}{u} \frac{d u}{d x}=\log x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{d u}{d x}=u[\log x \cdot 1+x \cdot \frac{1}{x}]$
$\Rightarrow \frac{d u}{d x}=x^{x}[\log x+1]=x^{x}(1+\log x)$
$v=x^{a}$
$\therefore \frac{d v}{d x}=\frac{d}{d x}(x^{a})$
$\Rightarrow \frac{d v}{d x}=a x^{a-1}$
$w=a^{x}$
$\Rightarrow \log w=\log a^{x}$
$\Rightarrow \log w=x \log a$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{w} \cdot \frac{d w}{d x}=\log a \cdot \frac{d}{d x}(x)$
$\Rightarrow \frac{d w}{d x}=w \log a$
$\Rightarrow \frac{d w}{d x}=a^{x} \log a$
$s=a^{a}$
Since $a$ is constant, $a^{a}$ is also a constant.
$\therefore \frac{d s}{d x}=0$
From (1), (2), (3), (4), and (5), we obtain
$ \begin{aligned} \frac{d y}{d x} & =x^{x}(1+\log x)+a x^{a-1}+a^{x} \log a+0 \\ & =x^{x}(1+\log x)+a x^{a-1}+a^{x} \log a \end{aligned} $
11. $x^{x^{2}-3}+(x-3)^{x^{2}}$, for $x>3$
Show Answer
Solution
Let $y=x^{x^{2}-3}+(x-3)^{x^{2}}$
Also, let $u=x^{x^{2}-3}$ and $v=(x-3)^{x^{2}}$
$\therefore y=u+v$
Differentiating both sides with respect to $x$, we obtain
$\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}$
$u=x^{x^{2}-3}$
$\therefore \log u=\log (x^{x^{2}-3})$
$\log u=(x^{2}-3) \log x$
Differentiating with respect to $x$, we obtain
$\frac{1}{u} \cdot \frac{d u}{d x}=\log x \cdot \frac{d}{d x}(x^{2}-3)+(x^{2}-3) \cdot \frac{d}{d x}(\log x)$
$\Rightarrow \frac{1}{u} \frac{d u}{d x}=\log x \cdot 2 x+(x^{2}-3) \cdot \frac{1}{x}$
$\Rightarrow \frac{d u}{d x}=x^{x^{2}-3} \cdot[\frac{x^{2}-3}{x}+2 x \log x]$
Also,
$v=(x-3)^{x^{2}}$
$\therefore \log v=\log (x-3)^{x^{2}}$
$\Rightarrow \log v=x^{2} \log (x-3)$
Differentiating both sides with respect to $x$, we obtain $\frac{1}{v} \cdot \frac{d v}{d x}=\log (x-3) \cdot \frac{d}{d x}(x^{2})+x^{2} \cdot \frac{d}{d x}[\log (x-3)]$
$\Rightarrow \frac{1}{v} \frac{d v}{d x}=\log (x-3) \cdot 2 x+x^{2} \cdot \frac{1}{x-3} \cdot \frac{d}{d x}(x-3)$
$\Rightarrow \frac{d v}{d x}=v[2 x \log (x-3)+\frac{x^{2}}{x-3} \cdot 1]$
$\Rightarrow \frac{d v}{d x}=(x-3)^{x^{2}}[\frac{x^{2}}{x-3}+2 x \log (x-3)]$
Substituting the expressions of $\frac{d u}{d x}$ and $\frac{d v}{d x}$ in equation (1), we obtain
$\frac{d y}{d x}=x^{x^{2}-3}[\frac{x^{2}-3}{x}+2 x \log x]+(x-3)^{x^{2}}[\frac{x^{2}}{x-3}+2 x \log (x-3)]$
12. Find $\frac{d y}{d x}$, if $y=12(1-\cos t), x=10(t-\sin t),-\frac{\pi}{2}<t<\frac{\pi}{2}$
Show Answer
Solution
It is given that, $y=12(1-\cos t), x=10(t-\sin t)$
$\therefore \frac{d x}{d t}=\frac{d}{d t}[10(t-\sin t)]=10 \cdot \frac{d}{d t}(t-\sin t)=10(1-\cos t)$
$\frac{d y}{d t}=\frac{d}{d t}[12(1-\cos t)]=12 \cdot \frac{d}{d t}(1-\cos t)=12 \cdot[0-(-\sin t)]=12 \sin t$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{12 \sin t}{10(1-\cos t)}=\frac{12 \cdot 2 \sin \frac{t}{2} \cdot \cos \frac{t}{2}}{10 \cdot 2 \sin ^{2} \frac{t}{2}}=\frac{6}{5} \cot \frac{t}{2}$
13. Find $\frac{d y}{d x}$, if $y=\sin ^{-1} x+\sin ^{-1} \sqrt{1-x^{2}}, 0<x<1$
Show Answer
Solution
It is given that, $y=\sin ^{-1} x+\sin ^{-1} \sqrt{1-x^{2}}$
$\therefore \frac{d y}{d x}=\frac{d}{d x}[\sin ^{-1} x+\sin ^{-1} \sqrt{1-x^{2}}]$
$\Rightarrow \frac{d y}{d x}=\frac{d}{d x}(\sin ^{-1} x)+\frac{d}{d x}(\sin ^{-1} \sqrt{1-x^{2}})$
$\Rightarrow \frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}+\frac{1}{\sqrt{1-(\sqrt{1-x^{2}})^{2}}} \cdot \frac{d}{d x}(\sqrt{1-x^{2}})$
$\Rightarrow \frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}+\frac{1}{x} \cdot \frac{1}{2 \sqrt{1-x^{2}}} \cdot \frac{d}{d x}(1-x^{2})$
$\Rightarrow \frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}+\frac{1}{2 x \sqrt{1-x^{2}}}(-2 x)$
$\Rightarrow \frac{d y}{d x}=\frac{1}{\sqrt{1-x^{2}}}-\frac{1}{\sqrt{1-x^{2}}}$
$\therefore \frac{d y}{d x}=0$
14. If $x \sqrt{1+y}+y \sqrt{1+x}=0$, for , $-1<x<1$, prove that $ \frac{d y}{d x}=-\frac{1}{(1+x)^{2}} $
Show Answer
Solution
It is given that,
$x \sqrt{1+y}+y \sqrt{1+x}=0$ $\Rightarrow x \sqrt{1+y}=-y \sqrt{1+x}$
Squaring both sides, we obtain
$x^{2}(1+y)=y^{2}(1+x)$
$\Rightarrow x^{2}+x^{2} y=y^{2}+x y^{2}$
$\Rightarrow x^{2}-y^{2}=x y^{2}-x^{2} y$
$\Rightarrow x^{2}-y^{2}=x y(y-x)$
$\Rightarrow(x+y)(x-y)=x y(y-x)$
$\therefore x+y=-x y$
$\Rightarrow(1+x) y=-x$
$\Rightarrow y=\frac{-x}{(1+x)}$
Differentiating both sides with respect to $x$, we obtain
$y=\frac{-x}{(1+x)}$
$\frac{d y}{d x}=-\frac{(1+x) \frac{d}{d x}(x)-x \frac{d}{d x}(1+x)}{(1+x)^{2}}=-\frac{(1+x)-x}{(1+x)^{2}}=-\frac{1}{(1+x)^{2}}$
Hence, proved.
15. If $(x-a)^{2}+(y-b)^{2}=c^{2}$, for some $c>0$, prove that $ \frac{[1+(\frac{d y}{d x})^{2}]^{\frac{3}{2}}}{\frac{d^{2} y}{d x^{2}}}$ is a constant independent of $a$ and $b$.
Show Answer
Solution
It is given that, $(x-a)^{2}+(y-b)^{2}=c^{2}$
Differentiating both sides with respect to $x$, we obtain
$$ \begin{align*} & \frac{d}{d x}[(x-a)^{2}]+\frac{d}{d x}[(y-b)^{2}]=\frac{d}{d x}(c^{2}) \\ & \Rightarrow 2(x-a) \cdot \frac{d}{d x}(x-a)+2(y-b) \cdot \frac{d}{d x}(y-b)=0 \\ & \Rightarrow 2(x-a) \cdot 1+2(y-b) \cdot \frac{d y}{d x}=0 \\ & \Rightarrow \frac{d y}{d x}=\frac{-(x-a)}{y-b} \tag{1}\\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[\frac{-(x-a)}{y-b}] \end{align*} $$
$ \begin{aligned} & =-[\frac{(y-b) \cdot \frac{d}{d x}(x-a)-(x-a) \cdot \frac{d}{d x}(y-b)}{(y-b)^{2}}] \\ & =-[\frac{(y-b)-(x-a) \cdot \frac{d y}{d x}}{(y-b)^{2}}] \\ & =-[\frac{(y-b)-(x-a) \cdot{\frac{-(x-a)}{y-b}}}{(y-b)^{2}}] \\ & =-[\frac{(y-b)^{2}+(x-a)^{2}}{(y-b)^{3}}] \\ & \therefore[\frac{1+(\frac{d y}{d x})^{2}}{\frac{d^{2} y}{d x^{2}}}]^{\frac{3}{2}}=\frac{[1+\frac{(x-a)^{2}}{(y-b)^{2}}]^{\frac{3}{2}}}{-[\frac{(y-b)^{2}+(x-a)^{2}}{(y-b)^{3}}]}=\frac{[\frac{(y-b)^{2}+(x-a)^{2}}{(y-b)^{2}}]^{\frac{3}{2}}}{-[\frac{(y-b)^{2}+(x-a)^{2}}{(y-b)^{3}}]} \\ & =\frac{[\frac{c^{2}}{(y-b)^{2}}]^{\frac{3}{2}}}{-\frac{c^{2}}{(y-b)^{3}}}=\frac{\frac{c^{3}}{(y-b)^{3}}}{-\frac{c^{2}}{(y-b)^{3}}} \end{aligned} $
$ =-c \text{, which is constant and is independent of } a \text{ and } b $
Hence, proved.
16. If $\cos y=x \cos (a+y)$, with $\cos a \neq \pm 1$, prove that $\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}$.
Show Answer
Solution
It is given that, $\cos y=x \cos (a+y)$
$\therefore \frac{d}{d x}[\cos y]=\frac{d}{d x}[x \cos (a+y)]$
$\Rightarrow-\sin y \frac{d y}{d x}=\cos (a+y) \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}[\cos (a+y)]$
$\Rightarrow-\sin y \frac{d y}{d x}=\cos (a+y)+x \cdot[-\sin (a+y)] \frac{d y}{d x}$
$\Rightarrow[x \sin (a+y)-\sin y] \frac{d y}{d x}=\cos (a+y)$
Since $\cos y=x \cos (a+y), x=\frac{\cos y}{\cos (a+y)}$
Then, equation (1) reduces to
$[\frac{\cos y}{\cos (a+y)} \cdot \sin (a+y)-\sin y] \frac{d y}{d x}=\cos (a+y)$
$\Rightarrow[\cos y \cdot \sin (a+y)-\sin y \cdot \cos (a+y)] \cdot \frac{d y}{d x}=\cos ^{2}(a+y)$
$\Rightarrow \sin (a+y-y) \frac{d y}{d x}=\cos ^{2}(a+b)$
$\Rightarrow \frac{d y}{d x}=\frac{\cos ^{2}(a+b)}{\sin a}$
Hence, proved.
17. If $x=a(\cos t+t \sin t)$ and $y=a(\sin t-t \cos t)$, find $\frac{d^{2} y}{d x^{2}}$.
Show Answer
Solution
It is given that, $x=a(\cos t+t \sin t)$ and $y=a(\sin t-t \cos t)$
$\therefore \frac{d x}{d t}=a \cdot \frac{d}{d t}(\cos t+t \sin t)$
$=a[-\sin t+\sin t \cdot \frac{d}{d x}(t)+t \cdot \frac{d}{d t}(\sin t)]$
$=a[-\sin t+\sin t+t \cos t]=a t \cos t$
$\frac{d y}{d t}=a \cdot \frac{d}{d t}(\sin t-t \cos t)$
$=a[\cos t-{\cos t \cdot \frac{d}{d t}(t)+t \cdot \frac{d}{d t}(\cos t)}]$
$=a[\cos t-{\cos t-t \sin t}]=a t \sin t$
$\therefore \frac{d y}{d x}=\frac{(\frac{d y}{d t})}{(\frac{d x}{d t})}=\frac{a t \sin t}{a t \cos t}=\tan t$
Then, $\frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(\frac{d y}{d x})=\frac{d}{d x}(\tan t)=\sec ^{2} t \cdot \frac{d t}{d x}$
$ \begin{aligned} & =\sec ^{2} t \cdot \frac{1}{a t \cos t} \quad[\frac{d x}{d t}=a t \cos t \Rightarrow \frac{d t}{d x}=\frac{1}{a t \cos t}] \\ & =\frac{\sec ^{3} t}{a t}, 0<t<\frac{\pi}{2} \end{aligned} $
18. If $f(x)=|x|^{3}$, show that $f^{\prime \prime}(x)$ exists for all real $x$ and find it.
Show Answer
Solution
It is known that, $|x|= \begin{cases}x, & \text{ if } x \geq 0 \\ -x, & \text{ if } x<0\end{cases}$
Therefore, when $x \geq 0, f(x)=|x|^{3}=x^{3}$
In this case, $f^{\prime}(x)=3 x^{2}$ and hence, $f^{\prime \prime}(x)=6 x$
When $x<0, f(x)=|x|^{3}=(-x)^{3}=-x^{3}$
In this case, $f^{\prime}(x)=-3 x^{2}$ and hence, $f^{\prime \prime}(x)=-6 x$
Thus, for $f(x)=|x|^{3}, f^{\prime \prime}(x)$ exists for all real $x$ and is given by,
$f^{\prime \prime}(x)= \begin{cases}6 x, & \text{ if } x \geq 0 \\ -6 x, & \text{ if } x<0\end{cases}$
19. Using the fact that $\sin (A+B)=\sin A \cos B+\cos A \sin B$ and the differentiation, obtain the sum formula for cosines.
Show Answer
Solution
$\sin (A+B)=\sin A \cos B+\cos A \sin B$
Differentiating both sides with respect to $x$, we obtain
$ \begin{aligned} & \frac{d}{d x}[\sin (A+B)]=\frac{d}{d x}(\sin A \cos B)+\frac{d}{d x}(\cos A \sin B) \\ & \Rightarrow \cos (A+B) \cdot \frac{d}{d x}(A+B)=\cos B \cdot \frac{d}{d x}(\sin A)+\sin A \cdot \frac{d}{d x}(\cos B) \\ & +\sin B \cdot \frac{d}{d x}(\cos A)+\cos A \cdot \frac{d}{d x}(\sin B) \\ & \Rightarrow \cos (A+B) \cdot \frac{d}{d x}(A+B)=\cos B \cdot \cos A \frac{d A}{d x}+\sin A(-\sin B) \frac{d B}{d x} \\ & +\sin B(-\sin A) \cdot \frac{d A}{d x}+\cos A \cos B \frac{d B}{d x} \\ & \Rightarrow \cos (A+B) \cdot[\frac{d A}{d x}+\frac{d B}{d x}]=(\cos A \cos B-\sin A \sin B) \cdot[\frac{d A}{d x}+\frac{d B}{d x}] \\ & \therefore \cos (A+B)=\cos A \cos B-\sin A \sin B \end{aligned} $
20. Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer.
Show Answer
Solution21. If $y=\left|\begin{array}{lll}f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c\end{array}\right| $ , prove that $\frac{d y}{d x}=\left|\begin{array}{lll}f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c\end{array}\right| $
Show Answer
Solution
$ \begin{aligned} & y= \begin{vmatrix} f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c \end{vmatrix} \\ & \Rightarrow y=(m c-n b) f(x)-(l c-n a) g(x)+(l b-m a) h(x) \end{aligned} $
Then, $\frac{d y}{d x}=\frac{d}{d x}[(m c-n b) f(x)]-\frac{d}{d x}[(l c-n a) g(x)]+\frac{d}{d x}[(l b-m a) h(x)]$
$ =(m c-n b) f^{\prime}(x)-(l c-n a) g^{\prime}(x)+(l b-m a) h^{\prime}(x) $
$ = \begin{vmatrix} f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c \end{vmatrix} $
Thus, $\frac{d y}{d x}= \begin{vmatrix} f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c\end{vmatrix} $
22. If $y=e^{a \cos ^{-1} x},-1 \leq x \leq 1$, show that $(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y=0$.
Show Answer
Solution
It is given that, $y=e^{a \cos ^{-1} x}$
Taking logarithm on both the sides, we obtain
$\log y=a \cos ^{-1} x \log e$
$\log y=a \cos ^{-1} x$
Differentiating both sides with respect to $x$, we obtain
$\frac{1}{y} \frac{d y}{d x}=a \times \frac{-1}{\sqrt{1-x^{2}}}$
$\Rightarrow \frac{d y}{d x}=\frac{-a y}{\sqrt{1-x^{2}}}$
By squaring both the sides, we obtain
$(\frac{d y}{d x})^{2}=\frac{a^{2} y^{2}}{1-x^{2}}$
$\Rightarrow(1-x^{2})(\frac{d y}{d x})^{2}=a^{2} y^{2}$
$(1-x^{2})(\frac{d y}{d x})^{2}=a^{2} y^{2}$
Again differentiating both sides with respect to $x$, we obtain
$(\frac{d y}{d x})^{2} \frac{d}{d x}(1-x^{2})+(1-x^{2}) \times \frac{d}{d x}[(\frac{d y}{d x})^{2}]=a^{2} \frac{d}{d x}(y^{2})$
$\Rightarrow(\frac{d y}{d x})^{2}(-2 x)+(1-x^{2}) \times 2 \frac{d y}{d x} \cdot \frac{d^{2} y}{d x^{2}}=a^{2} \cdot 2 y \cdot \frac{d y}{d x}$
$\Rightarrow(\frac{d y}{d x})^{2}(-2 x)+(1-x^{2}) \times 2 \frac{d y}{d x} \cdot \frac{d^{2} y}{d x^{2}}=a^{2} \cdot 2 y \cdot \frac{d y}{d x}$
$\Rightarrow-x \frac{d y}{d x}+(1-x^{2}) \frac{d^{2} y}{d x^{2}}=a^{2} \cdot y \quad[\frac{d y}{d x} \neq 0]$
$\Rightarrow(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y=0$
Hence, proved.
Summary
-
A real valued function is continuous at a point in its domain if the limit of the function at that point equals the value of the function at that point. A function is continuous if it is continuous on the whole of its domain.
-
Sum, difference, product and quotient of continuous functions are continuous. i.e., if $f$ and $g$ are continuous functions, then
$(f \pm g)(x)=f(x) \pm g(x)$ is continuous.
$(f . g)(x)=f(x) \cdot g(x)$ is continuous.
$(\frac{f}{g})(x)=\frac{f(x)}{g(x)}$ (wherever $.g(x) \neq 0)$ is continuous.
- Every differentiable function is continuous, but the converse is not true.
- Chain rule is rule to differentiate composites of functions. If $f=v$ o $u, t=u(x)$ and if both $\frac{d t}{d x}$ and $\frac{d v}{d t}$ exist then
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x} $$
- Following are some of the standard derivatives (in appropriate domains):
$$ \begin{array}{ll} \frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^{2}}} & \frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^{2}}} \\ \frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^{2}} & \frac{d}{d x}(\log x)=\frac{1}{x} \end{array} $$
- Logarithmic differentiation is a powerful technique to differentiate functions of the form $f(x)=[u(x)]^{v(x)}$. Here both $f(x)$ and $u(x)$ need to be positive for this technique to make sense.
The whole of science is nothing more than a refinement of everyday thinking." - ALBERT EINSTEIN
5.1 भूमिका (Introduction)
यह अध्याय अनिवार्यतः कक्षा 11 में पढ़े गए फलनों के अवकलन (differentiation) का क्रमागत है। हम कुछ निश्चित बहुपदीय फलनों एवं त्रिकोणमितीय फलनों का अवकलन करना सीख चुके हैं। इस अध्याय में हम सांतत्य (continuity), अवकलनीयता (differentiability) तथा इनके पारस्परिक संबंधों की महत्वपर्ण संकल्पनाओं को प्रस्तुत करेंगे। यहाँ हम प्रतिलोम त्रिकोणमितीय (inverse trigonometric) फलनों का अवकलन करना भी सीखेंगे। अब हम कुछ नए प्रकार के फलनों को प्रस्तुत कर रहे हैं, जिनको चरघातांकी (exponential) और लघुगणकीय (logarithmic) फलन कहते हैं। इन फलनों द्वारा हमें अवकलन की सशक्त प्रविधियों का ज्ञान होता है। अवकल गणित (differential calculus) के माध्यम से हम ज्यामितीय रूप से सुस्पष्ट (obvious) कुछ स्थितियों को समझाते हैं। इस प्रक्रिया, में हम इस विषय की कुछ आधारभूत (मूल) प्रमेयों (theorems) को सीखेंगे।

5.2 सांतत्य (Continuity)
सांतत्य की संकल्पना का कुछ अनुमान (बोध) कराने के लिए, हम अनुच्छेद को दो अनौपचारिक उदाहरणों से प्रारंभ करते हैं। निम्नलिखित फलन पर विचार कीजिए:
$$ f(x)=\begin{cases} 1, \text{ यदि } x \leq 0 \\ 2, \text{ यदि } x>0 \end{cases}. $$
यह फलन वास्तव में वास्तविक रेखा (real line) के प्रत्येक बिंदु पर परिभाषित है। इस फलन का आलेख आकृति 5.1 में दर्शाया गया है। कोई भी इस आलेख से निष्कर्ष निकाल सकता है कि $x=0$ के अतिरिक्त, $x$-अक्ष के अन्य सन्निकट बिंदुओं के लिए फलन के संगत मान भी $x=0$ को छोड़कर एक दूसरे के समीप (लगभग समान) हैं। 0 के सन्निकट बायीं ओर के बिंदुओं, अर्थात् $-0.1,-0.01,-0.001$, प्रकार के बिंदुओं, पर फलन का मान 1 है तथा 0 के सन्निकट दायीं ओर के बिंदुओं, अर्थात् $0.1,0.01$, 0.001

, प्रकार के बिंदुओं पर फलन का मान 2 है। बाएँ और दाएँ पक्ष की सीमाओं (limits) की भाषा का प्रयोग करके, हम कह सकते हैं कि $x=0$ पर फलन $f$ के बाएँ तथा दाएँ पक्ष की सीमाएँ क्रमशः 1 तथा 2 हैं। विशेष रूप से बाएँ तथा दाएँ पक्ष की सीमाएँ समान / संपाती (coincident) नहीं हैं। हम यह भी देखते हैं कि $x=0$ पर फलन का मान बाएँ पक्ष की सीमा के संपाती है (बराबर है)। नोट कीजिए कि इस आलेख को हम लगातार एक साथ (in one stroke), अर्थात् कलम को इस कागज़ की सतह से बिना उठाए, नहीं खींच सकते। वास्तव में, हमें कलम को उठाने की आवश्यकता तब होती है जब हम शून्य से बायीं ओर आते हैं। यह एक उदाहरण है जहाँ फलन $x=0$ पर संतत (continuous) नहीं है।
अब नीचे दर्शाए गए फलन पर विचार कीजिए:
$$ f(x)=\begin{cases} & 1, \text{ यदि } x \neq 0 \\ & 2, \text{ यदि } x=0 \end{cases} $$
यह फलन भी प्रत्येक बिंदु पर परिभाषित है। $x=0$ पर दोनों ही, बाएँ तथा दाएँ पक्ष की सीमाएँ 1 के बराबर हैं। किंतु $x=0$ पर फलन का मान 2 है, जो बाएँ और दाएँ पक्ष की सीमाओं के उभयनिष्ठ मान के बराबर नहीं है। पुनः हम नोट करते हैं कि फलन के आलेख को बिना कलम उठाए हम नहीं खींच सकते हैं। यह एक दूसरा उदाहरण है जिसमें $x=0$ पर फलन संतत नहीं है। सहज रूप से (naively) हम कह सकते हैं कि
एक अचर बिंदु पर कोई फलन संतत है, यदि उस बिंदु के आस-पास (around) फलन के आलेख को हम कागज़ की सतह से कलम उठाए बिना खींच सकते हैं। इस बात को हम गणितीय भाषा में, यथातथ्य (precisely), निम्नलिखित प्रकार से व्यक्त कर सकते हैं:

निम्नलिखित प्रकार से व्यक्त कर सकते हैं:
परिभाषा 1 मान लीजिए कि $f$ वास्तविक संख्याओं के किसी उपसमुच्चय में परिभाषित एक वास्तविक फलन है और मान लीजिए कि $f$ के प्रांत में $c$ एक बिंदु है। तब $f$ बिंदु $c$ पर संतत है, यदि
$$ \lim _{x \rightarrow c} f(x)=f(c) \text { है। } $$
विस्तृत रूप से यदि $x=c$ पर बाएँ पक्ष की सीमा, दाएँ पक्ष की सीमा तथा फलन के मान का यदि अस्तित्व (existence) है और ये सभी एक दूसरे के बराबर हों, तो $x=c$ पर $f$ संतत कहलाता है। स्मरण कीजिए कि यदि $x=c$ पर बाएँ पक्ष तथा दाएँ पक्ष की सीमाएँ संपाती हैं, तो इनके उभयनिष्ठ मान को हम $x=c$ पर फलन की सीमा कहते हैं। इस प्रकार हम सांतत्य की परिभाषा को एक अन्य प्रकार से भी व्यक्त कर सकते हैं, जैसा कि नीचे दिया गया है। एक फलन $x=c$ पर संतत है, यदि फलन $x=c$ पर परिभाषित है और यदि $x=c$ पर फलन का मान $x=c$ पर फलन की सीमा के बराबर है। यदि $x=c$ पर फलन संतत नहीं है तो हम कहते हैं कि $c$ पर $f$ असंतत (discontinuous) है तथा $c$ को $f$ का एक असांतत्य का बिंदु (point of discontinuity) कहते हैं।
उदाहरण 1 $x=1$ पर फलन $f(x)=2 x+3$ के सांतत्य की जाँच कीजिए।
हल पहले यह ध्यान दीजिए कि फलन, $x=1$ पर परिभाषित है और इसका मान 5 है। अब फलन की $x=1$ पर सीमा ज्ञात करते हैं। स्पष्ट है कि
$$ \begin{aligned} & \lim _{x \rightarrow 1} f(x)=\lim _{x \rightarrow 1}(2 x+3)=2(1)+3=5 \text { है। } \\ \end{aligned} $$
अत: $\qquad \lim _{x \to 1} f(x)=5=f(1)$
अतएव $x=1$ पर $f$ संतत है।
उदाहरण 2 जाँचिए कि क्या फलन $f(x)=x^{2}, x=0$ पर संतत है?
हल ध्यान दीजिए कि प्रदत्त बिंदु $x=0$ पर फलन परिभाषित है और इसका मान 0 है। अब $x=0$ पर फलन की सीमा निकालते हैं। स्पष्टतया
$$ \lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0} x^{2}=0^{2}=0 $$
इस प्रकार $\qquad\lim _{x \rightarrow 0} f(x)=0=f(0)$
अत: $ x=0 \text { पर } f \text { संतत है। } $
उदाहरण 3 $x=0$ पर फलन $f(x)=|x|$ के सांतत्य पर विचार कीजिए।
हल परिभाषा द्वारा
$$ f(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases} $$
स्पष्टतया $x=0$ पर फलन परिभाषित है और $f(0)=0$ है। बिंदु $x=0$ पर $f$ की बाएँ पक्ष की सीमा
$$ \lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{-}}(-x)=0 \text { है। } $$
इसी प्रकार 0 पर $f$ की दाएँ पक्ष की सीमा के लिए
$$ \lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{+}} x=0 \text { है। } $$
इस प्रकार $x=0$ पर बाएँ पक्ष की सीमा, दाएँ पक्ष की सीमा तथा फलन का मान संपाती हैं। अत: $x=0$ पर $f$ संतत है।
उदाहरण 4 दर्शाइए कि फलन
$$ f(x)= \begin{cases}x^{3}+3, & \text { यदि } x \neq 0 \\ 1, & \text { यदि } x=0\end{cases} $$
$x=0$ पर संतत नहीं है।
हल यहाँ $x=0$ पर फलन परिभाषित है और $x=0$ पर इसका मान 1 है। जब $x \neq 0$, तब फलन बहुपदीय है। इसलिए
$$ \lim _{x \rightarrow 0} f(x)=\lim _{x \rightarrow 0}\left(x^{3}+3\right)=0^{3}+3=3 $$
क्योंकि $x=0$ पर $f$ की सीमा, $f(0)$ के बराबर नहीं है, इसलिए $x=0$ पर फलन संतत नहीं है। हम यह भी सुनिश्चित कर सकते हैं कि इस फलन के लिए असांतत्य का बिंदु केवल $x=0$ है।
उदाहरण 5 उन बिंदुओं की जाँच कीजिए जिन पर अचर फलन (Constant function) $f(x)=k$ संतत है।
हल यह फलन सभी वास्तविक संख्याओं के लिए परिभाषित है और किसी भी वास्तविक संख्या के लिए इसका मान $k$ है। मान लीजिए कि $c$ एक वास्तविक संख्या है, तो
$$ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} k=k $$
चूँकि किसी वास्तविक संख्या $c$ के लिए $f(c)=k=\lim _{x \rightarrow c} f(x)$ है इसलिए फलन $f$ प्रत्येक वास्तविक संख्या के लिए संतत है।
उदाहरण 6 सिद्ध कीजिए कि वास्तविक संख्याओं के लिए तत्समक फलन (Identity function) $f(x)=x$, प्रत्येक वास्तविक संख्या के लिए संतत है।
हल स्पष्टतया यह फलन प्रत्येक बिंदु पर परिभाषित है और प्रत्येक वास्तविक संख्या $c$ के लिए $f(c)=c$ है।
साथ ही $ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} x=c $
इस प्रकार, $\lim _{x \rightarrow c} f(x)=c=f(c)$ और इसलिए यह फलन $f$ के प्रांत के सभी बिंदुओं पर संतत है ।
एक प्रदत्त बिंदु पर किसी फलन के सांतत्य को परिभाषित करने के बाद अब हम इस परिभाषा का स्वाभाविक प्रसार (extension) करके किसी फलन के, उसके प्रांत में, सांतत्य पर विचार करेंगे।
परिभाषा 2 एक वास्तविक फलन $f$ संतत कहलाता है यदि वह $f$ के प्रांत के प्रत्येक बिंदु पर संतत है। इस परिभाषा को कुछ विस्तार से समझने की आवश्यकता है। मान लीजिए कि $f$ एक ऐसा फलन है, जो संवृत अंतराल (closed interval) $[a, b]$ में परिभाषित है, तो $f$ के संतत होने के लिए आवश्यक है कि वह $[a, b]$ के अंत्य बिंदुओं (end points) $a$ तथा $b$ सहित उसके प्रत्येक बिंदु पर संतत हो। $f$ का अंत्य बिंदु $a$ पर सांतत्य का अर्थ है कि और $f$ का $b$ पर सांतत्य का अर्थ है कि
$$ \lim _{x \rightarrow a^{+}} f(x)=f(a) $$
$$ \lim _{x \rightarrow b^{-}} f(x)=f(b) $$
प्रेक्षण कीजिए कि $\lim _{x \rightarrow a^{-}} f(x)$ तथा $\lim _{x \rightarrow b^{+}} f(x)$ का कोई अर्थ नहीं है। इस परिभाषा के परिणामस्वरूप, यदि $f$ केवल एक बिंदु पर परिभाषित है, तो वह उस बिंदु पर संतत होता है, अर्थात् यदि $f$ का प्रांत एकल (समुच्चय) है, तो $f$ एक संतत फलन होता है।
उदाहरण 7 क्या $f(x)=|x|$ द्वारा परिभाषित फलन एक संतत फलन है?
हल $f$ को हम ऐसे लिख सकते हैं कि
$ f(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases} $
उदाहरण 3 से हम जानते हैं कि $x=0$ पर $f$ संतत है।
मान लीजिए कि $c$ एक वास्तविक संख्या इस प्रकार है कि $c<0$ है। अतएव $f(c)=-c$
साथ ही $ \begin{equation*} \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(-x)=-c \tag{क्यों?} \end{equation*} $
चूँकि $\lim _{x \rightarrow c} f(x)=f(c)$, इसलिए $f$ सभी ऋणात्मक वास्तविक संख्याओं के लिए संतत है।
अब मान लीजिए कि $c$ एक वास्तविक संख्या इस प्रकार है कि $c>0$ है। अतएव $f(c)=c$ साथ ही
$$ \begin{equation*} \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} x=c \tag{क्यों?} \end{equation*} $$
क्योंकि $\lim _{x \rightarrow c} f(x)=f(c)$, इसलिए $f$ सभी धनात्मक वास्तविक संख्याओं के लिए संतत है। चूँकि $f$ सभी बिंदुओं पर संतत है, अतः यह एक संतत फलन है।
उदाहरण 8 फलन $f(x)=x^{3}+x^{2}-1$ के सांतत्य पर विचार कीजिए।
हल स्पष्टतया $f$ प्रत्येक वास्तविक संख्या $c$ के लिए परिभाषित है और $c$ पर इसका मान $c^{3}+c^{2}-1$ है। हम यह भी जानते हैं कि
$$ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}\left(x^{3}+x^{2}-1\right)=c^{3}+c^{2}-1 $$
अतः $\lim _{x \rightarrow c} f(x)=f(c)$ है इसलिए प्रत्येक वास्तविक संख्या के लिए $f$ संतत है। इसका अर्थ है कि $f$ एक संतत फलन है।
उदाहरण 9 $f(x)=\frac{1}{x}, x \neq 0$ द्वारा परिभाषित फलन $f$ के सांतत्य पर विचार कीजिए।
हल किसी एक शून्येतर ( Non-zero) वास्तविक संख्या $c$ को सुनिश्चित कीजिए अब
$$ \lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} \frac{1}{x}=\frac{1}{c} $$
साथ ही, चूँकि $c \neq 0$, इसलिए $f(c)=\frac{1}{c}$ है। इस प्रकार $\lim _{x \rightarrow c} f(x)=f(c)$ और इसलिए $f$ अपने प्रांत के प्रत्येक बिंदु पर संतत है। इस प्रकार $f$ एक संतत फलन है।
हम इस अवसर का लाभ, अनंत (infinity) की संकल्पना (concept) को समझाने के लिए, उठाते हैं। हम इसके लिए फलन $f(x)=\frac{1}{x}$ का विश्लेषण $x=0$ के निकटस्थ मानों पर करते हैं। इसके लिए हम 0 के सन्निकट की वास्तविक संख्याओं के लिए फलन के मानों का अध्ययन करने की प्रचलित युक्ति का प्रयोग करते हैं। अनिवार्यतः (essentially) हम $x=0$ पर $f$ के दाएँ पक्ष की सीमा ज्ञात करने का प्रयास करते हैं। इसको हम नीचे सारणीबद्ध करते हैं। (सारणी 5.1)
सारणी 5.1
| x | 1 | 0.3 | 0.2 | $0.=10^{-1}$ | $ 0.01=10^{-2} $ | $ 0.001=10^{-3} $ | $ 10^n $ |
|---|---|---|---|---|---|---|---|
| f(x) | 1 | 3.333… | 5 | 10 | $ 100=10^2 $ | $1000=10^3$ | $ 10^n $ |
हम देखते हैं कि जैसे-जैसे $x$ दायीं ओर से 0 के निकट अग्रसर होता है $f(x)$ का मान उत्तरोत्तर अति शीघ्रता से बढ़ता जाता है। इस बात को एक अन्य प्रकार से भी व्यक्त किया जा सकता है, जैसे: एक धन वास्तविक संख्या को 0 के अत्यंत निकट चुनकर, $f(x)$ के मान को किसी भी प्रदत्त संख्या से अधिक किया जा सकता है। प्रतीकों में इस बात को हम निम्नलिखित प्रकार से लिखते हैं कि
$$ \lim _{x \rightarrow 0^{+}} f(x)=+\infty $$
(इसको इस प्रकार पढ़ा जाता है: 0 पर, $f(x)$ के दाएँ पक्ष की धनात्मक सीमा अनंत है)। यहाँ पर हम बल देना चाहते हैं कि $+\infty$ एक वास्तविक संख्या नहीं है और इसलिए 0 पर $f$ के दाएँ पक्ष की सीमा का अस्तित्व नहीं है (वास्तविक संख्याओं के रूप में)।
इसी प्रकार से 0 पर $f$ के बाएँ पक्ष की सीमा ज्ञात की जा सकती है। निम्नलिखित सारणी से स्वतः स्पष्ट है।
सारणी 5.2
| $x$ | -1 | -0.3 | -0.2 | $-10^{-1}$ | $-10^{-2}$ | $-10^{-3}$ | $-10^{-n}$ |
|---|---|---|---|---|---|---|---|
| $f(x)$ | -1 | $-3.333 \ldots$ | -5 | -10 | $-10^{2}$ | $-10^{3}$ | $-10^{n}$ |
सारणी 5.2 से हम निष्कर्ष निकालते हैं कि एक ॠणात्मक वास्तविक संख्या को 0 के अत्यंत निकट चुनकर, $f(x)$ के मान को किसी भी प्रदत्त संख्या से कम किया जा सकता है। प्रतीकात्मक रूप से हम
$$ \lim _{x \rightarrow 0^{-}} f(x)=-\infty \text { लिखते हैं } $$
(जिसे इस प्रकार पढ़ा जाता है: 0 पर $f(x)$ के बाएँ पक्ष की सीमा ऋणात्मक अनंत है।) यहाँ हम इस बात पर बल देना चाहते हैं कि - $\infty$ एक वास्तविक संख्या नहीं है अतएव 0 पर $f$ के बाएँ पक्ष की सीमा का अस्तित्व नहीं है (वास्तविक संख्याओं के रूप में)। आकृति 5.3 का आलेख उपर्युक्त तथ्यों का ज्यामितीय निरूपण है।

आकृति 5.3
उदाहरण 10 निम्नलिखित फलन के सांतत्य पर विचार कीजिए:
$$ f(x)= \begin{cases}-x, & \text{ if } x<0 \\ x, & \text{ if } x \geq 0\end{cases} $$
हल फलन $f$ वास्तविक रेखा के प्रत्येक बिंदु पर परिभाषित है।
दशा 1 यदि $c<1$, तो $f(c)=c+2$ है। इस प्रकार $\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} x+2=c+2$ है।
अतः 1 से कम सभी वास्तविक संख्याओं पर $f$ संतत है।
दशा 2 यदि $c>1$, तो $f(c)=c-2$ है।
इसलिए $\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(x-2)=c-2=f(c)$ है।
अतएव उन सभी बिंदुओं पर जहाँ $x>1$ है, $f$ संतत है।
दशा 3 यदि $c=1$, तो $x=1$ पर $f$ के बाएँ पक्ष की सीमा, अर्थात्
$$ \lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}(x+2)=1+2=3 $$
$x=1$ पर $f$ के दाएँ पक्ष की सीमा, अर्थात्
$$ \lim _{x \rightarrow 1^{+}} f(x)=\lim _{x \rightarrow 1^{-}}(x-2)=1-2=-1 $$
अब चूँकि $x=1$ पर $f$ के बाएँ तथा दाएँ पक्ष की सीमाएँ संपाती (coincident) नहीं हैं, अतः $x=1$ पर $f$ संतत नहीं है। इस प्रकार $f$ के असांतत्य का बिंदु

आकृति 5.4
केवल मात्र $x=1$ है। इस फलन का आलेख आकृति 5.4 में दर्शाया गया है।
उदाहरण 11 निम्नलिखित प्रकार से परिभाषित फलन $f$ के समस्त (सभी) असांतत्य बिंदुओं को ज्ञात कीजिए
$$ f(x)=\begin{cases} x+2, \text{ यदि } x<1 \\ 0, \text{ यदि } \quad x=1 \\ x-2, \text{ यदि } x>1 \end{cases}. $$
हल पूर्ववर्ती उदाहरण की तरह यहाँ भी हम देखते हैं प्रत्येक वास्तविक संख्या $x \neq 1$ के लिए $f$ संतत है। $x=1$ के लिए $f$ के बाएँ पक्ष की सीमा,
$\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}(x+2)=1+2=3$ है।
$x=1$ के लिए $f$ के दाएँ पक्ष की सीमा,
$\lim _{x \rightarrow 1^{-}} f(x)=\lim _{x \rightarrow 1^{-}}(x-2)=1-2=-1$ है।
चूँकि $x=1$ पर $f$ के बाएँ तथा दाएँ पक्ष की सीमाएँ संपाती नहीं हैं, अतः $x=1$ पर $f$ संतत नहीं है। इस प्रकार $f$ के असांतत्य का बिंदु केवल मात्र $x=1$ है। इस फलन का आलेख आकृति 5.5 में दर्शाया गया है।

आकृति 5.5
उदाहरण 12 निम्नलिखित फलन के सांतत्य पर विचार कीजिए:
$$ f(x)=\begin{cases} x+2, \text{ यदि } x<0 \\ -x+2, \text{ यदि } x>0 \end{cases}. $$
हल ध्यान दीजिए कि विचाराधीन फलन 0 (शून्य) के अतिरिक्त अन्य समस्त वास्तविक संख्याओं के लिए परिभाषित है। परिभाषानुसार इस फलन का प्रांत
$$ \begin{aligned} \mathrm{D} _{1} \cup \mathrm{D} _{2} \text { है जहाँ } \mathrm{D} _{1} & =\{x \in \mathbf{R}: x<0\} \text { और } \\ \mathrm{D} _{2} & =\{x \in \mathbf{R}: x>0\} \text { है। } \end{aligned} $$
दशा 1
यदि $c \in \mathrm{D} _{1}$, तो $\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(x+2)=$ $c+2=f(c)$ है अतएव $\mathrm{D} _{1}$ में $f$ संतत है।
दशा 2
यदि $c \in \mathrm{D} _{2}$, तो $\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(-x+2)=$ $-c+2=f(c)$ है
अतएव $\mathrm{D} _{2}$ में भी $f$ संतत है। क्योंकि $f$ अपने प्रांत के समस्त बिंदुओं पर संतत है जिससे हम निष्कर्ष निकालते हैं कि $f$ एक संतत फलन है। इस फलन का आलेख आकृति 5.6 में खींचा गया है। ध्यान दीजिए कि इस फलन के आलेख को खींचने के लिए हमें कलम को कागज़ की सतह से उठाना पड़ता है, किंतु हमें ऐसा केवल उन बिंदुओं पर करना पड़ता है जहाँ पर फलन परिभाषित नहीं है।

आकृति 5.6
उदाहरण 13 निम्नलिखित फलन के सांतत्य पर विचार कीजिए:
$$ f(x)= \begin{cases}x, & \text { यदि } x \geq 0 \\ x^{2}, & \text { यदि } x<0\end{cases} $$
हल स्पष्टतया, प्रदत्त फलन प्रत्येक वास्तविक संख्या के लिए परिभाषित है। इस फलन का आलेख आकृति 5.7 में दिया है। इस आलेख के निरीक्षण से यह तर्कसंगत लगता है कि फलन के प्रांत को वास्तविक रेखा के तीन असंयुक्त (disjoint) उप समुच्चयों में विभाजित कर लिया जाए।
मान लिया कि $\qquad \begin{aligned}& \mathrm{D} _{1}=\{x \in \mathbf{R}: x<0\}, \mathrm{D} _{2}=\{0\} \text { तथा } \& \mathrm{D} _{3}=\{x \in \mathbf{R}: x>0\} \text { है। }\end{aligned}$

आकृति 5.7
दशा $1 \mathrm{D} _{1}$ के किसी भी बिंदु पर $f(x)=x^{2}$ है और यह सरलता से देखा जा सकता है कि $\mathrm{D} _{1}$ में $f$ संतत है। (उदाहरण 2 देखिए)
दशा $2 \mathrm{D} _{3}$ के किसी भी बिंदु पर $f(x)=x$ है और यह सरलता से देखा जा सकता है कि $\mathrm{D} _{3}$ में $f$ संतत है। (उदाहरण 6 देखिए)
दशा 3 अब हम $x=0$ पर फलन का विश्लेषण करते हैं। 0 के लिए फलन का मान $f(0)=0$ है। 0 पर $f$ के बाएँ पक्ष की सीमा
$$ \lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{-}} x^{2}=0^{2}=0 \text { है तथा } $$
0 पर $f$ के दाएँ पक्ष की सीमा
$$ \lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{+}} x=0 \text { है। } $$
अतः $\lim _{x \rightarrow 0} f(x)=0=f(0)$ अतएव 0 पर $f$ संतत है। इसका अर्थ यह हुआ कि $f$ अपने प्रांत के प्रत्येक बिंदु पर संतत है। अतः $f$ एक संतत फलन है।
उदाहरण 14 दर्शाइए कि प्रत्येक बहुपद फलन संतत होता है।
हल स्मरण कीजिए कि कोई फलन $p$, एक बहुपद फलन होता है यदि वह किसी प्राकृत संख्या $n$ के लिए $p(x)=a _{0}+a _{1} x+\ldots+a _{n} x^{n}$ द्वारा परिभाषित हो, जहाँ $a _{i} \in \mathbf{R}$ तथा $a _{n} \neq 0$ है। स्पष्टतया यह फलन प्रत्येक वास्तविक संख्या के लिए परिभाषित है। किसी निश्चित वास्तविक संख्या $c$ के लिए हम देखते हैं कि
$$ \lim _{x \rightarrow c} p(x)=p(c) $$
इसलिए परिभाषा द्वारा $c$ पर $p$ संतत है। चूँकि $c$ कोई भी वास्तविक संख्या है इसलिए $p$ किसी भी वास्तविक संख्या के लिए संतत है, अर्थात् $p$ एक संतत फलन है।
उदाहरण $15 f(x)=[x]$ द्वारा परिभाषित महत्तम पूर्णांक फलन के असांतत्य के समस्त बिंदुओं को ज्ञात कीजिए, जहाँ $[x]$ उस महत्तम पूर्णांक को प्रकट करता है, जो $x$ से कम या उसके बराबर है।
हल पहले तो हम यह देखते हैं कि $f$ सभी वास्तविक संख्याओं के लिए परिभाषित है। इस फलन का आलेख आकृति 5.8 में दिखाया गया है।आलेख से ऐसा प्रतीत होता है कि प्रदत्त फलन $x$ के सभी पूर्णांक मानों के लिए असंतत है। नीचे हम छानबीन करेंगे कि क्या यह सत्य है।

आकृति 5.8
दशा 1 मान लीजिए कि $c$ एक ऐसी वास्तविक संख्या है, जो किसी भी पूर्णांक के बराबर नहीं है। आलेख से यह स्पष्ट है कि $c$ के निकट की सभी वास्तविक संख्याओं के लिए दिए हुए फलन का मान $[c]$; हैं, अर्थात् $\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}[x]=[c]$ साथ ही $f(c)=[c]$ अतः प्रदत्त फलन, उन सभी वास्तविक संख्याओं के लिए संतत है, जो पूर्णांक नहीं है।
दशा 2 मान लीजिए कि $c$ एक पूर्णांक है। अतएव हम एक ऐसी पर्याप्ततः छोटी वास्तविक संख्या $r>0$ प्राप्त कर सकते हैं जो कि $[c-r]=c-1$ जबकि $[c+r]=c$ है।
सीमाओं के रूप में, इसका अर्थ यह हुआ कि
$$ \lim _{x \rightarrow c^{-}} f(x)=c-1 \text { तथा } \lim _{x \rightarrow c^{+}} f(x)=c $$
चूँकि किसी भी पूर्णांक $c$ के लिए ये सीमाएँ समान नहीं हो सकती हैं, अतः प्रदत्त फलन $x$ सभी पूर्णांक मानों के लिए असंतत है।
5.2.1 संतत फलनों का बीजगणित (Algebra of continuous functions)
पिछली कक्षा में, सीमा की संकल्पना समझने के उपरांत, हमनें सीमाओं के बीजगणित का कुछ अध्ययन किया था। अनुरूपतः अब हम संतत फलनों के बीजगणित का भी कुछ अध्ययन करेंगे। चूँकि किसी बिंदु पर एक फलन का सांतत्य पूर्णरूप से उस बिंदु पर फलन की सीमा द्वारा निर्धारित होता है, अतएव यह तर्कसंगत है कि हम सीमाओं के सदृश्य ही यहाँ भी बीजीय परिणामों की अपेक्षा करें।
प्रमेय 1 मान लीजिए कि $f$ तथा $g$ दो ऐसे वास्तविक फलन हैं, जो एक वास्तविक संख्या $c$ के लिए संतत हैं। तब,
(1) $f+g, x=c$ पर संतत है
(2) $f-g, x=c$ पर संतत है
(3) $f . g, x=c$ पर संतत है
(4) $\left(\frac{f}{g}\right), x=c$ पर संतत है (जबकि $g(c) \neq 0$ है।)
उपपत्ति हम बिंदु $x=c$ पर $(f+g)$ के सांतत्य की जाँच करते हैं। हम दखते हैं कि
$ \begin{aligned} \lim _{x \to c}(f+g)(x) & =\lim _{x \to c}[f(x)+g(x)] & & (f+g \text { की परिभाषा द्वारा }) \\ & =\lim _{x \to c} f(x)+\lim _{x \to c} g(x) & & \text{ (सीमाओं के प्रमेय द्वारा) } \\ & =f(c)+g(c) & & (\text { क्यों } f \text { तथा } g \text { संतत फलन हैं }) \\ & =(f+g)(c) & & (f+g \text { की परिभाषा द्वारा }) \end{aligned} $
अतः, $f+g$ भी $x=c$ के लिए संतत है।
प्रमेय 1 के शेष भागों की उपपत्ति इसी के समान है जिन्हें पाठकों के लिए अभ्यास हेतु छोड़ दिया गया है।
टिप्पणी
(i) उपर्युक्त प्रमेय के भाग (3) की एक विशेष दशा के लिए, यदि $f$ एक अचर फलन $f(x)=\lambda$ हो, जहाँ $\lambda$, कोई अचर वास्तविक संख्या है, तो $(\lambda . g)(x)=\lambda . g(x)$ द्वारा परिभाषित फलन $(\lambda . g)$ भी एक संतत फलन है। विशेष रूप से, यदि $\lambda=-1$, तो $f$ के सांतत्य में $-f$ का सांतत्य अंतर्निहित होता है।
(ii) उपर्युक्त प्रमेय के भाग (4) की एक विशेष दशा के लिए, यदि $f$ एक अचर फलन $f(x)=\lambda$, तो $\frac{\lambda}{g}(x)=\frac{\lambda}{g(x)}$ द्वारा परिभाषित फलन $\frac{\lambda}{g}$ भी एक संतत फलन होता है, जहाँ $g(x) \neq 0$ है। विशेष रूप से, $g$ के सांतत्य में $\frac{1}{g}$ का सांतत्य अंतर्निहित है।
उपर्युक्त दोनों प्रमेयों के उपयोग द्वारा अनेक संतत फलनों को बनाया जा सकता है। इनसे यह निश्चित करने में भी सहायता मिलती है कि कोई फलन संतत है या नहीं। निम्नलिखित उदाहरणों में यह बात स्पष्ट की गई है।
उदाहरण 16 सिद्ध कीजिए कि प्रत्येक परिमेय फलन संतत होता है।
हल स्मरण कीजिए कि प्रत्येक परिमेय फलन $f$ निम्नलिखित रूप का होता है:
$$ f(x)=\frac{p(x)}{q(x)}, q(x) \neq 0 $$
जहाँ $p$ और $q$ बहुपद फलन हैं। $f$ का प्रांत, उन बिंदुओं को छोड़कर जिन पर $q$ शून्य है, समस्त वास्तविक संख्याएँ हैं। चूँकि बहुपद फलन संतत होते हैं (उदाहरण 14), अतएव प्रमेय 1 के भाग (4) द्वारा $f$ एक संतत फलन है।
उदाहरण 17 sine फलन के सांतत्य पर विचार कीजिए।
हल इस पर विचार करने के लिए हम निम्नलिखित तथ्यों का प्रयोग करते हैं:
$$ \lim _{x \rightarrow 0} \sin x=0 $$
हमने इन तथ्यों को यहाँ प्रमाणित तो नहीं किया है, किन्तु sine फलन के आलेख को शून्य के निकट देख कर ये तथ्य सहजानुभूति (intuitively) से स्पष्ट हो जाता है।
अब देखिए कि $f(x)=\sin x$ सभी वास्तविक संख्याओं के लिए परिभाषित है। मान लीजिए कि $c$ एक वास्तविक संख्या है। $x=c+h$ रखने पर, यदि $x \rightarrow c$ तो हम देखते हैं कि $h \rightarrow 0$ इसलिए
$$ \begin{aligned} \lim _{x \rightarrow c} f(x) & =\lim _{x \rightarrow c} \sin x \\ & =\lim _{h \rightarrow 0} \sin (c+h) \\ & =\lim _{h \rightarrow 0}[\sin c \cos h+\cos c \sin h] \\ & =\lim _{h \rightarrow 0}[\sin c \cos h]+\lim _{h \rightarrow 0}[\cos c \sin h] \\ & =\sin c+0=\sin c=f(c) \end{aligned} $$
इस प्रकार $\lim _{x \rightarrow c} f(x)=f(c)$ अतः $f$ एक संतत फलन है।
टिप्पणी इसी प्रकार cosine फलन के सांतत्य को भी प्रमाणित किया जा सकता है।
उदाहरण 18 सिद्ध कीजिए कि $f(x)=\tan x$ एक संतत फलन है।
हल दिया हुआ फलन $f(x)=\tan x=\frac{\sin x}{\cos x}$ है। यह फलन उन सभी वास्तविक संख्याओं के लिए परिभाषित है, जहाँ $\cos x \neq 0$, अर्थात् $x \neq(2 n+1) \frac{\pi}{2}$ है। हमने अभी प्रमाणित किया है कि sine और cosine फलन, संतत फलन हैं। इसलिए $\tan$ फलन, इन दोनों फलनों का भागफल होने के कारण, $x$ के उन सभी मानों के लिए संतत है जिन के लिए यह परिभाषित है।
फलनों के संयोजन (composition) से संबंधित, संतत फलनों का व्यवहार एक रोचक तथ्य है। स्मरण कीजिए कि यदि $f$ और $g$ दो वास्तविक फलन हैं, तो
$$ (f \circ g)(x)=f(g(x)) $$
परिभाषित है, जब कभी $g$ का परिसर $f$ के प्रांत का एक उपसमुच्चय होता है। निम्नलिखित प्रमेय (प्रमाण बिना केवल व्यक्त), संयुक्त (composite) फलनों के सांतत्य को परिभाषित करती है। प्रमेय 2 मान लीजिए कि $f$ और $g$ इस प्रकार के दो वास्तविक मानीय (real valued) फलन हैं कि $c$ पर $(f \circ g)$ परिभाषित है। यदि $c$ पर $g$ तथा $g(c)$ पर $f$ संतत है, तो $c$ पर $(f \circ g)$ संतत होता है।
निम्नलिखित उदाहरणों में इस प्रमेय को स्पष्ट किया गया है।
उदाहरण 19 दर्शाइए कि $f(x)=\sin \left(x^{2}\right)$ द्वारा परिभाषित फलन, एक संतत फलन है।
हल प्रेक्षण कीजिए कि विचाराधीन फलन प्रत्येक वास्तविक संख्या के लिए परिभाषित है। फलन $f$ को, $g$ तथा $h$ दो फलनों के संयोजन $(g \circ h)$ के रूप में सोचा जा सकता है, जहाँ $g(x)=\sin x$ तथा $h(x)=x^{2}$ है। चूँकि $g$ और $h$ दोनों ही संतत फलन हैं, इसलिए प्रमेय 2 द्वारा यह निष्कर्ष निकाला जा सकता है, कि $f$ एक संतत फलन है।
उदाहरण 20 दर्शाइए कि $f(x)=|1-x+| x||$ द्वारा परिभाषित फलन $f$,
जहाँ $x$ एक वास्तविक संख्या है, एक संतत फलन है।
हल सभी वास्तविक संख्याओं $x$ के लिए $g$ को $g(x)=1-x+|x|$ तथा $h$ को $h(x)=|x|$ द्वारा परिभाषित कीजिए। तब,
$$ \begin{aligned} (h \circ g)(x) & =h(g(x)) \\ & =h(1-x+|x|) \\ & =|1-x+| x||=f(x) \end{aligned} $$
उदाहरण 7 में हम देख चुके हैं कि $h$ एक संतत फलन है। इसी प्रकार एक बहुपद फलन और एक मापांक फलन का योग होने के कारण $g$ एक संतत फलन है। अतः दो संतत फलनों का संयुक्त फलन होने के कारण $f$ भी एक संतत फलन है।
प्रश्नावली 5.1
1. सिद्ध कीजिए कि फलन $f(x)=5 x-3, x=0, x=-3$ तथा $x=5$ पर संतत है।
Show Answer
#missing2. $x=3$ पर फलन $f(x)=2 x^{2}-1$ के सांतत्य की जाँच कीजिए।
Show Answer
#missing3. निम्नलिखित फलनों के सांतत्य की जाँच कीजिए:
(a) $f(x)=x-5$
(b) $f(x)=\frac{1}{x-5}, x \neq 5$ (c) $f(x)=\frac{x^{2}-25}{x+5}, x \neq-5$
(d) $f(x)=|x-5|$
Show Answer
#missing4. सिद्ध कीजिए कि फलन $f(x)=x^{n}, x=n$, पर संतत है, जहाँ $n$ एक धन पूर्णांक है।
Show Answer
#missing5. क्या $f(x)=\left\{\begin{array}{l}x, \text { यदि } x \leq 1 \\ 5, \text { यदि } x>1\end{array}\right.$
द्वारा परिभाषित फलन $f$ $x=0, x=1$, तथा $x=2$ पर संतत है?
$f$ के सभी असांतत्य के बिंदुओं को ज्ञात कीजिए, जब कि $f$ निम्नलिखित प्रकार से परिभाषित है:
Show Answer
#missing6. $f(x)=\left\{\begin{array}{l}2 x+3, \text { यदि } x \leq 2 \\ 2 x-3, \text { यदि } x>2\end{array}\right.$
Show Answer
#missing7. $f(x)=\left\{\begin{array}{l}|x|+3, \text { यदि } x \leq-3 \\ -2 x, \text { यदि }-3<x<3 \\ 6 x+2, \text { यदि } x \geq 3\end{array}\right.$
Show Answer
#missing8. $f(x)= \begin{cases}\frac{|x|}{x}, & \text { यदि } x \neq 0 \\ 0, & \text { यदि } x=0\end{cases}$
Show Answer
#missing9. $f(x)= \begin{cases}\frac{x}{|x|}, & \text { यदि } x<0 \\ -1, & \text { यदि } x \geq 0\end{cases}$
Show Answer
#missing10. $f(x)=\left\{\begin{array}{l}x+1, \text { यदि } x \geq 1 \\ x^{2}+1, \text { यदि } x<1\end{array}\right.$
Show Answer
#missing11. $f(x)= \begin{cases}x^{3}-3, & \text { यदि } x \leq 2 \\ x^{2}+1, & \text { यदि } x>2\end{cases}$
Show Answer
#missing12. $f(x)= \begin{cases}x^{10}-1, & \text { यदि } x \leq 1 \\ x^{2}, & \text { यदि } x>1\end{cases}$
Show Answer
#missing13. क्या $ f(x)= \begin{cases}x+5, & \text{ if } x \leq 1 \\ x-5, & \text{ if } x>1\end{cases} $ द्वारा परिभाषित फलन, एक संतत फलन है?
फलन $f$, के सांतत्य पर विचार कीजिए, जहाँ $f$ निम्नलिखित द्वारा परिभाषित है:
Show Answer
#missing14. $f(x)=\left\{\begin{array}{l}3, \text { यदि } 0 \leq x \leq 1 \\ 4, \text { यदि } 1<x<3 \\ 5, \text { यदि } 3 \leq x \leq 10\end{array}\right.$
Show Answer
#missing15. $f(x)= \begin{cases}2 x, & \text { यदि } x<0 \\ 0, & \text { यदि } 0 \leq x \leq 1 \\ 4 x, & \text { यदि } x>1\end{cases}$
Show Answer
#missing16. $f(x)= \begin{cases}-2, & \text { यदि } x \leq-1 \\ 2 x, & \text { यदि }-1<x \leq 1 \\ 2, & \text { यदि } x>1\end{cases}$
Show Answer
#missing17. $a$ और $b$ के उन मानों को ज्ञात कीजिए जिनके लिए
$$ f(x)= \begin{cases}a x+1, & \text { यदि } x \leq 3 \\ b x+3, & \text { यदि } x>3\end{cases} $$
द्वारा परिभाषित फलन $x=3$ पर संतत है।
Show Answer
#missing18. $\lambda$ के किस मान के लिए
$$ f(x)= \begin{cases}\lambda\left(x^{2}-2 x\right), & \text { यदि } x \leq 0 \\ 4 x+1, & \text { यदि } x>0\end{cases} $$
द्वारा परिभाषित फलन $x=0$ पर संतत है। $x=1$ पर इसके सांतत्य पर विचार कीजिए।
Show Answer
#missing19. दर्शाइए कि $g(x)=x-[x]$ द्वारा परिभाषित फलन समस्त पूर्णांक बिंदुओं पर असंतत है। यहाँ $[x]$ उस महत्तम पूर्णांक निरूपित करता है, जो $x$ के बराबर या $x$ से कम है।
Show Answer
#missing20. क्या $f(x)=x^{2}-\sin x+5$ द्वारा परिभाषित फलन $x=\pi$ पर संतत है?
21. निम्नलिखित फलनों के सांतत्य पर विचार कीजिए:
(a) $f(x)=\sin x+\cos x$
(b) $f(x)=\sin x-\cos x$
(c) $f(x)=\sin x \cdot \cos x$
Show Answer
#missing22. cosine, cosecant, secant और cotangent फलनों के सांतत्य पर विचार कीजिए।
Show Answer
#missing23. $f$ के सभी असांतत्यता के बिंदुओं को ज्ञात कीजिए, जहाँ
$$ f(x)= \begin{cases}\frac{\sin x}{x}, & \text { यदि } x<0 \\ x+1, & \text { यदि } x \geq 0\end{cases} $$
Show Answer
#missing24. निर्धारित कीजिए कि फलन $f$
$$ f(x)= \begin{cases}x^{2} \sin \frac{1}{x}, & \text { यदि } x \neq 0 \\ 0, & \text { यदि } x=0\end{cases} $$
द्वारा परिभाषित एक संतत फलन है।
Show Answer
#missing25. $f$ के सांतत्य की जाँच कीजिए, जहाँ $f$ निम्नलिखित प्रकार से परिभाषित है
$$ f(x)= \begin{cases}\sin x-\cos x, & \text { यदि } x \neq 0 \\ -1, & \text { यदि } x=0\end{cases} $$
Show Answer
#missingप्रश्न 26 से 29 में $k$ के मानों को ज्ञात कीजिए ताकि प्रदत्त फलन निर्दिष्ट बिंदु पर संतत हो:
26. $f(x)=\left\{\begin{array}{ll}\frac{k \cos x}{\pi-2 x}, & \text { यदि } x \neq \frac{\pi}{2} \\ 3, & \text { यदि } x=\frac{\pi}{2}\end{array} \quad\right.$ द्वारा परिभाषित फलन $x=\frac{\pi}{2}$ पर
Show Answer
#missing27. $f(x)= \begin{cases}k x^{2}, & \text { यदि } x \leq 2 \\ 3, & \text { यदि } x>2\end{cases}$
Show Answer
#missing28. $f(x)= \begin{cases}k x+1, & \text { यदि } x \leq \pi \\ \cos x, & \text { यदि } x>\pi\end{cases}$ द्वारा परिभाषित फलन $x=\pi$ पर
Show Answer
#missing29. $f(x)= \begin{cases}k x+1, & \text { यदि } x \leq 5 \\ 3 x-5, & \text { यदि } x>5\end{cases}$ द्वारा परिभाषित फलन $x=5$ पर
Show Answer
#missing30. $a$ तथा $b$ के मानों को ज्ञात कीजिए ताकि
$$ f(x)= \begin{cases}5, & \text { यदि } x \leq 2 \\ a x+b, & \text { यदि } 2<x<10 \\ 21, & \text { यदि } x \geq 10\end{cases} $$
द्वारा परिभाषित फलन एक संतत फलन हो।
Show Answer
#missing31. दर्शाइए कि $f(x)=\cos \left(x^{2}\right)$ द्वारा परिभाषित फलन एक संतत फलन है।
Show Answer
#missing32. दर्शाइए कि $f(x)=|\cos x|$ द्वारा परिभाषित फलन एक संतत फलन है।
Show Answer
#missing33. जाँचिए कि क्या $\sin |x|$ एक संतत फलन है।
Show Answer
#missing34. $f(x)=|x|-|x+1|$ द्वारा परिभाषित फलन $f$ के सभी असांत्यता के बिंदुओं को ज्ञात कीजिए।
Show Answer
#missing5.3. अवकलनीयता (Differentiability)
पिछली कक्षा में सीखे गए तथ्यों को स्मरण कीजिए। हमनें एक वास्तविक फलन के अवकलज (Derivative) को निम्नलिखित प्रकार से परिभाषित किया था।
मान लीजिए कि $f$ एक वास्तविक फलन है तथा $c$ इसके प्रांत में स्थित एक बिंदु है। $c$ पर $f$ का अवकलज निम्नलिखित प्रकार से परिभाषित है:
$$ \lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h} $$
यदि इस सीमा का अस्तित्व हो तो $c$ पर $f$ के अवकलज को $f^{\prime}(c)$ या $\left.\frac{d}{d x}(f(x))\right| _{c}$ द्वारा प्रकट करते हैं।
$$ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
द्वारा परिभाषित फलन, जब भी इस सीमा का अस्तित्व हो, $f$ के अवकलज को परिभाषित करता है। $f$ के अवकलज को $f^{\prime}(x)$ या $\frac{d}{d x}(f(x))$ द्वारा प्रकट करते हैं और यदि $y=f(x)$ तो इसे $\frac{d y}{d x}$ या $y^{\prime}$ द्वारा प्रकट करते हैं। किसी फलन का अवकलज ज्ञात करने की प्रक्रिया को अवकलन (differentiation)कहते हैं। हम वाक्यांश " $x$ के सापेक्ष $f(x)$ का अवकलन कीजिए (differentiate)" का भी प्रयोग करते हैं, जिसका अर्थ होता है कि $f^{\prime}(x)$ ज्ञात कीजिए।
अवकलज के बीजगणित के रूप में निम्नलिखित नियमों को प्रमाणित किया जा चुका है:
(1) $(u \pm v)^{\prime}=u^{\prime} \pm v^{\prime}$.
(2) $(u v)^{\prime}=u^{\prime} v+u v^{\prime}$ (लेबनीज़ या गुणनफल नियम)
(3) $\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$, जहाँ $v \neq 0$ (भागफल नियम)
नीचे दी गई सारणी में कुछ प्रामाणिक (standard) फलनों के अवकलजों की सूची दी गई है:
सारणी 5.3
| $f(x)$ | $x^{n}$ | $\sin x$ | $\cos x$ | $\tan x$ |
|---|---|---|---|---|
| $f^{\prime}(x)$ | $n x^{n-1}$ | $\cos x$ | $-\sin x$ | $\sec ^{2} x$ |
जब कभी भी हमने अवकलज को परिभाषित किया है तो एक सुझाव भी दिया है कि “यदि सीमा का अस्तित्व हो।" अब स्वाभाविक रूप से प्रश्न उठता है कि यदि ऐसा नहीं है तो क्या होगा? यह प्रश्न नितांत प्रासंगिक है और इसका उत्तर भी। यदि $\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}$ का अस्तित्व नहीं है, तो हम कहते हैं कि $c$ पर $f$ अवकलनीय नहीं है। दूसरे शब्दों में, हम कहते हैं कि अपने प्रांत के किसी बिंदु $c$ पर फलन $f$ अवकलनीय है, यदि दोनों सीमाएँ $\lim _{h \rightarrow 0^{-}} \frac{f(c+h)-f(c)}{h}$ तथा $\lim _{h \rightarrow 0^{+}} \frac{f(c+h)-f(c)}{h}$ परिमित (finite) तथा समान हैं। फलन अंतराल $[a, b]$ में अवकलनीय कहलाता है, यदि वह अंतराल $[a, b]$ के प्रत्येक बिंदु पर अवकलनीय है। जैसा कि सांतत्य के संदर्भ में कहा गया था कि अंत्य बिंदुओं $a$ तथा $b$ पर हम क्रमशः दाएँ तथा बाएँ पक्ष की सीमाएँ लेते हैं, जो कि और कुछ नहीं, बल्कि $a$ तथा $b$ पर फलन के दाएँ पक्ष तथा बाएँ पक्ष के अवकलज ही हैं। इसी प्रकार फलन अंतराल $(a, b)$ में अवकलनीय कहलाता है, यदि वह अंतराल $(a, b)$ के प्रत्येक बिंदु पर अवकलनीय है।
प्रमेय 3 यदि फलन किसी बिंदु $c$ पर अवकलनीय है, तो उस बिंदु पर वह संतत भी है।
उपपत्ति चूँकि बिंदु $c$ पर $f$ अवकलनीय है, अतः
$$ \lim _{x \rightarrow c} \frac{f(x)-f(c)}{x-c}=f^{\prime}(c) $$
किंतु $x \neq c$ के लिए
$$ f(x)-f(c)=\frac{f(x)-f(c)}{x-c} .(x-c) $$
$ \text{इसलिए} \qquad \begin{aligned} \lim _{x \to c}[f(x)-f(c)] & =\lim _{x \to c}[\frac{f(x)-f(c)}{x-c} \cdot(x-c)] \\ \lim _{x \to c}[f(x)]-\lim _{x \to c}[f(c)] & =\lim _{x \to c}[\frac{f(x)-f(c)}{x-c}] \cdot \lim _{x \to c}[(x-c)] \\ & =f^{\prime}(c) \cdot 0=0 \\ \lim _{x \to c} f(x) & =f(c) \end{aligned} $
इस प्रकार $x=c$ पर फलन $f$ संतत है।
उपप्रमेय 1 प्रत्येक अवकलनीय फलन संतत होता है।
यहाँ हम ध्यान दिलाते हैं कि उपर्युक्त कथन का विलोम (converse) सत्य नहीं है। निश्चय ही हम देख चुके हैं कि $f(x)=|x|$ द्वारा परिभाषित फलन एक संतत फलन है। इस फलन के बाएँ पक्ष की सीमा पर विचार करने से
$$ \lim _{h \rightarrow 0^{-}} \frac{f(0+h)-f(0)}{h}=\frac{-h}{h}=-1 $$
तथा दाँए पक्ष की सीमा
$$ \lim _{h \rightarrow 0^{+}} \frac{f(0+h)-f(0)}{h}=\frac{h}{h}=1 \text { है। } $$
चूँकि 0 पर उपर्युक्त बाएँ तथा दाएँ पक्ष की सीमाएँ समान नहीं हैं, इसलिए $\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}$ का अस्तित्व नहीं है और इस प्रकार 0 पर $f$ अवकलनीय नहीं है। अतः $f$ एक अवकलनीय फलन नहीं है।
5.3.1 संयुक्त फलनों के अवकलज (Differentials of composite functions)
संयुक्त फलनों के अवकलज के अध्ययन को हम एक उदाहरण द्वारा स्पष्ट करेंगे। मान लीजिए कि हम $f$ का अवकलज ज्ञात करना चाहते हैं, जहाँ
$$ f(x)=(2 x+1)^{3} $$
एक विधि यह है कि द्विपद प्रमेय के प्रयोग द्वारा $(2 x+1)^{3}$ को प्रसारित करके प्राप्त बहुपद फलन का अवकलज ज्ञात करें, जैसा नीचे स्पष्ट किया गया है;
$$ \begin{aligned} \frac{d}{d x} f(x) & =\frac{d}{d x}\left[(2 x+1)^{3}\right] \\ & =\frac{d}{d x}\left(8 x^{3}+12 x^{2}+6 x+1\right) \\ & =24 x^{2}+24 x+6 \\ & =6(2 x+1)^{2} \end{aligned} $$
अब, ध्यान दीजिए कि
$$ f(x)=(h \circ g)(x) $$
जहाँ $g(x)=2 x+1$ तथा $h(x)=x^{3}$ है। मान लीजिए $t=g(x)=2 x+1$. तो $f(x)=h(t)=t^{3}$.
$\text{ अत: }\frac{d f}{d x}=6(2 x+1)^{2}=3(2 x+1)^{2} \cdot 2=3 t^{2} \cdot 2=\frac{d h}{d t} \cdot \frac{d t}{d x}$
इस दूसरी विधि का लाभ यह है कि कुछ प्रकार के फलन, जैसे $(2 x+1)^{100}$ के अवकलज का परिकलन करना इस विधि द्वारा सरल हो जाता है। उपर्युक्त परिचर्चा से हमें औपचारिक रूप से निम्नलिखित प्रमेय प्राप्त होता है, जिसे श्रृंखला नियम (chain rule) कहते हैं।
प्रमेय 4(शृंखला नियम) मान लीजिए कि $f$ एक वास्तविक मानीय फलन है, जो $u$ तथा $v$ दो फलनों का संयोजन है; अर्थात् $f=v \mathrm{O} u$. मान लीजिए कि $t=u(x)$ और, यदि $\frac{d t}{d x}$ तथा $\frac{d v}{d t}$ दोनों का अस्तित्व है, तो
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x} $$
हम इस प्रमेय की उपपत्ति छोड़ देते हैं। भृंखला नियम का विस्तार निम्नलिखित प्रकार से किया जा सकता है। मान लीजिए कि $f$ एक वास्तविक मानीय फलन है, जो तीन फलनों $u, v$ और $w$ का संयोजन है, अर्थात्
$$ \begin{aligned} & f=(w \circ u) \circ v \text { है यदि } t=u(x) \text { तथा } s=v(t) \text { है तो } \\ & \frac{d f}{d x}=\frac{d}{d t}(w \circ u) \cdot \frac{d t}{d x}=\frac{d w}{d s} \cdot \frac{d s}{d t} \cdot \frac{d t}{d x} \end{aligned} $$
यदि उपर्युक्त कथन के सभी अवकलजों का अस्तित्व हो तो पाठक और अधिक फलनों के संयोजन के लिए श्रृंखला नियम को प्रयुक्त कर सकते हैं।
उदाहरण $21 f(x)=\sin \left(x^{2}\right)$ का अवकलज ज्ञात कीजिए।
हल ध्यान दीजिए कि प्रदत्त फलन दो फलनों का संयोजन है। वास्तव में, यदि $u(x)=x^{2}$ और $v(t)=\sin t$ है तो
$$ f(x)=(v \text { o } u)(x)=v(u(x))=v\left(x^{2}\right)=\sin x^{2} $$ $t=u(x)=x^{2}$ रखने पर ध्यान दीजिए कि $\frac{d v}{d t}=\cos t$ तथा $\frac{d t}{d x}=2 x$ और दोनों का अस्तित्व भी हैं। अतः शृंखला नियम द्वारा
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x}=\cos t .2 x $$
सामान्यतः अंतिम परिणाम को $x$ के पदों में व्यक्त करने का प्रचलन है अतएव
$$ \frac{d f}{d x}=\cos t \cdot 2 x=2 x \cos x^{2} $$
प्रश्नावली 5.2
प्रश्न 1 से 8 में $x$ के सापेक्ष निम्नलिखित फलनों का अवकलन कीजिए:
1. $\sin \left(x^{2}+5\right)$
Show Answer
#missing2. $\cos (\sin x)$
Show Answer
#missing3. $\sin (a x+b)$
Show Answer
#missing4. $\sec (\tan (\sqrt{x}))$
Show Answer
#missing5. $\frac{\sin (a x+b)}{\cos (c x+d)}$
Show Answer
#missing6. $\cos x^{3} \cdot \sin ^{2}\left(x^{5}\right)$
Show Answer
#missing7. $2 \sqrt{\cot \left(x^{2}\right)}$
Show Answer
#missing8. $\cos (\sqrt{x})$
Show Answer
#missing9. सिद्ध कीजिए कि फलन
$f(x)=|x-1|,x \in \mathbf{R}, x=1$
पर अवकलित नहीं है।
Show Answer
#missing10. सिद्ध कीजिए कि महत्तम पूर्णांक फलन
$f(x)=[x], 0<x<3, x=1$
तथा $x=2$ पर अवकलित नहीं है।
Show Answer
#missing5.3.2 अस्पष्ट फलनों के अवकलज (Derivatives of Implicit Functions)
अब तक हम $y=f(x)$ के रूप के विविध फलनों का अवकलन करते रहे हैं परंतु यह आवश्यक नहीं है कि फलनों को सदैव इसी रूप में व्यक्त किया जाए। उदाहरणार्थ, $x$ और $y$ के बीच निम्नलिखित संबंधों में से एक पर विशेष रूप से विचार कीजिए:
$$ \begin{array}{r} x-y-\pi=0 \\ x+\sin x y-y=0 \end{array} $$
पहली दशा में, हम $y$ के लिए सरल कर सकते हैं और संबंध को $y=x-\pi$ के रूप में लिख सकते हैं। दूसरी दशा में, ऐसा नहीं लगता है कि संबंध $y$ को सरल करने का कोई आसान तरीका है। फिर भी दोनों में से किसी भी दशा में, $y$ की $x$ पर निर्भरता के बारे में कोई संदेह नहीं है। जब $x$ और $y$ के बीच का संबंध इस प्रकार व्यक्त किया गया हो कि उसे $y$ के लिए सरल करना आसान हो और $y=f(x)$ के रूप में लिखा जा सके, तो हम कहते हैं कि $y$ को $x$ के स्पष्ट (explicit)फलन के रूप में व्यक्त किया गया है। उपर्युक्त दूसरे संबंध में, हम कहते हैं कि $y$ को $x$ के अस्पष्ट (implicity) फलन के रूप में व्यक्त किया गया है।
उदाहरण 22 यदि $x-y=\pi$ तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल एक विधि यह है कि हम $y$ के लिए सरल करके उपर्युक्त संबंध को निम्न प्रकार लिखें यथा
$$ \begin{aligned} y & =x-\pi \\ \end{aligned} $$
तव $\qquad\begin{aligned}\frac{d y}{d x} & =1\end{aligned}$
विकल्पतः इस संबंध का $x$, के सापेक्ष सीधे अवकलन करने पर
$$ \frac{d}{d x}(x-y)=\frac{d \pi}{d x} $$
याद कीजिए कि $\frac{d \pi}{d x}$ का अर्थ है कि $x$ के सापेक्ष एक अचर $\pi$ का अवकलन करना। इस प्रकार
$$ \frac{d}{d x}(x)-\frac{d}{d x}(y)=0 $$
जिसका तात्पर्य है कि $$ \frac{d y}{d x}=\frac{d x}{d x}=1 $$
उदाहरण 23 यदि $y+\sin y=\cos x$ तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल हम इस संबंध का सीधे अवकलज करते हैं।
शृंखला नियम का प्रयोग करने पर $\qquad \frac{d y}{d x}+\frac{d}{d x}(\sin y)=\frac{d}{d x}(\cos x)$
इससे निम्नलिखित परिणाम मिलता है, $\qquad \frac{d y}{d x}+\cos y \cdot \frac{d y}{d x}=-\sin x$
जहाँ $\qquad \begin{array}{r}\frac{d y}{d x}=-\frac{\sin x}{1+\cos y} \\y \neq(2 n+1) \pi\end{array}$
5.3.3 प्रतिलोम त्रिकोणमितीय फलनों के अवकलज (Derivatives of Inverse Trigonometric Functions)
हम पुन: ध्यान दिलाते हैं कि प्रतिलोम त्रिकोणमितीय फलन संतत होते हैं, परंतु हम इसे प्रमाणित नहीं करेंगे। अब हम इन फलनों के अवकलजों को ज्ञात करने के लिए भृंखला नियम का प्रयोग करेंगे।
उदाहरण 24 $f(x)=\sin ^{-1} x$ का अवकलज ज्ञात कीजिए। यह मान लीजिए कि इसका अस्तित्व है।
हल मान लीजिए कि $y=f(x)=\sin ^{-1} x$ है तो $x=\sin y$
दोनों पक्षों का $x$ के सापेक्ष अवकलन करने पर
$$ \begin{aligned} & 1=\cos y \frac{d y}{d x} \\ \text{ध्यान दीजिए कि यह केवल} \qquad \Rightarrow \quad & \frac{d y}{d x}=\frac{1}{\cos y}=\frac{1}{\cos \left(\sin ^{-1} x\right)} \end{aligned} $$
$\cos y \neq 0$ के लिए परिभाषित है, अर्थात् ,
$\sin ^{-1} x \neq-\frac{\pi}{2}, \frac{\pi}{2}$, अर्थात् $x \neq-1,1$, अर्थात् $x \in(-1,1)$
इस परिणाम को कुछ आकर्षक बनाने हेतु हम निम्नलिखित व्यवहार कौशल (manipulation) करते हैं। स्मरण कीजिए कि $x \in(-1,1)$ के लिए $\sin \left(\sin ^{-1} x\right)=x$ और इस प्रकार $\cos ^{2} y=1-(\sin y)^{2}=1-\left(\sin \left(\sin ^{-1} x\right)\right)^{2}=1-x^{2}$
साथ ही चूँकि $y \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right), \cos y$ एक धनात्मक राशि है और इसलिए $\cos y=\sqrt{1-x^{2}}$ इस प्रकार
$ \begin{aligned} & x \in(-1,1) \text { के लिए } \frac{d y}{d x}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-x^{2}}} \end{aligned} $
| $f(x)$ | $\sin ^{-1} x$ | $\cos ^{-1} x$ | $\tan ^{-1} x$ |
|---|---|---|---|
| $f^{\prime}(x)$ | $\frac{1}{\sqrt{1-x^{2}}}$ | $\frac{-1}{\sqrt{1-x^{2}}}$ | $\frac{1}{1+x^{2}}$ |
| Domain of $f^{\prime}$ | $(-1,1)$ | $(-1,1)$ | $\mathbf{R}$ |
प्रश्नावली 5.3
निम्नलिखित प्रश्नों में $\frac{d y}{d x}$ ज्ञात कीजिए
1. $2 x+3 y=\sin x$
Show Answer
#missing2. $2 x+3 y=\sin y$
Show Answer
#missing3. $a x+b y^{2}=\cos y$
Show Answer
#missing4. $x y+y^{2}=\tan x+y$
Show Answer
#missing5. $x^{2}+x y+y^{2}=100$
Show Answer
#missing6. $x^{3}+x^{2} y+x y^{2}+y^{3}=81$
Show Answer
#missing7. $\sin ^{2} y+\cos x y=k$
Show Answer
#missing8. $\sin ^{2} x+\cos ^{2} y=1$
Show Answer
#missing9. $y=\sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right)$
Show Answer
#missing10. $y=\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right),-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}$
Show Answer
#missing11. $y=\cos ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right), 0<x<1$
Show Answer
#missing12. $y=\sin ^{-1}\left(\frac{1-x^{2}}{1+x^{2}}\right), 0<x<1$
Show Answer
#missing13. $y=\cos ^{-1}\left(\frac{2 x}{1+x^{2}}\right),-1<x<1$
Show Answer
#missing14. $y=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right),-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}$
Show Answer
#missing15. $y=\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right), 0<x<\frac{1}{\sqrt{2}}$
Show Answer
#missing5.4 चरघातांकी तथा लघुगणकीय फलन (Exponential and Logarithmic Functions)
अभी तक हमने फलनों, जैसे बहुपद फलन, परिमेय फलन तथा त्रिकोणमितीय फलन, के विभिन्न वर्गों के कुछ पहलुओं के बारे में सीखा है। इस अनुच्छेद में हम परस्पर संबंधित फलनों के एक नए वर्ग के बारे में सीखेंगे, जिन्हें चरघातांकी (exponential) तथा लघुगणकीय (logarithmic) फलन कहते हैं। यहाँ पर विशेष रूप से यह बतलाना आवश्यक है कि इस अनुच्छेद के बहुत से कथन प्रेरक तथा यथातथ्य हैं और उनकी उपपत्तियाँ इस पुस्तक की विषय-वस्तु के क्षेत्र से बाहर हैं।
आकृति 5.9 में $y=f _{1}(x)=x, y=f _{2}(x)=x^{2}, y=f _{3}(x)=x^{3}$ तथा $y=f _{4}(x)=x^{4}$ के आलेख दिए गए हैं। ध्यान दीजिए कि ज्यों-ज्यों $x$ की घात बढ़ती जाती है वक्र की प्रवणता भी बढ़ती जाती है। वक्र की प्रवणता बढ़ने से वृद्धि की दर तेज होती जाती है। इसका अर्थ यह है कि $x(>1)$ के मान में निश्चित वृद्धि के संगत $y=f _{n}(x)$ का मान बढ़ता जाता है जैसे-जैसे $n$ का मान 1,2 , 3,4 होता जाता है। यह कल्पनीय है कि ऐसा कथन सभी धनात्मक मान के लिए सत्य है जहाँ $f _{n}(x)=x^{n}$ है। आवश्यकरूप से, इसका अर्थ यह हुआ कि जैसे-जैसे $n$ में वृद्धि होती जाती है $y=f _{n}(x)$ का आलेख $y$-अक्ष की ओर अधिक झुकता जाता है। उदाहरण के लिए $f _{10}(x)=x^{10}$ तथा $f _{15}(x)=x^{15}$ पर विचार कीजिए। यदि $x$ का मान 1 से बढ़कर 2 हो जाता है, तो $f _{10}$ का मान 1 से बढ़कर $2^{10}$ हो जाता है, जबकि $f _{15}$ का मान आकृति 5.9 1 से बढ़कर $2^{15}$ हो जाता है। इस प्रकार $x$ में समान वृद्धि के लिए, $f _{15}$ की वृद्धि $f _{10}$ की वृद्धि के अपेक्षा अधिक तीव्रता से होती है।
उपर्युक्त परिचर्चा का निष्कर्ष यह है कि बहुपद फलनों की वृद्धि उनके घात पर निर्भर करती है, अर्थात् घात बढ़ाते जाइए वृद्धि बढ़ती जाएगी। इसके उपरांत एक स्वाभाविक प्रश्न यह उठता है कि, क्या कोई ऐसा फलन है जो बहुपद फलनों की अपेक्षा अधिक तेजी से बढ़ता है? इसका उत्तर सकारात्मक है और इस प्रकार के फलन का एक उदाहरण $y=f(x)=10^{x}$ है

आकृति 5.9 1 से बढ़कर $2^{15}$ हो जाता है। इस प्रकार $x$ में समान वृद्धि के लिए, $f _{15}$ की वृद्धि $f _{10}$ की वृद्धि के अपेक्षा अधिक तीव्रता से होती है।
हमारा दावा यह है कि किसी धन पूर्णांक $n$ के लिए यह फलन $f$, फलन $f _{n}(x)=x^{n}$ की अपेक्षा अधिक तेजी से बढ़ता है। उदाहरण के लिए हम सिद्ध कर सकते हैं कि $f _{100}(x)=x^{100}$ की अपेक्षा $10^{x}$ अधिक तेजी से बढ़ता है। यह नोट कीजिए कि $x$ के बड़े मानों के लिए, जैसे $x=10^{3}$, $f _{100}(x)=\left(10^{3}\right)^{100}=10^{300}$ जबकि $f\left(10^{3}\right)=10^{10^{3}}=10^{1000}$ है। स्पष्टतः $f _{100}(x)$ की अपेक्षा $f(x)$
का मान बहुत अधिक है। यह सिद्ध करना कठिन नहीं है कि $x$ के उन सभी मानों के लिए जहाँ $x>10^{3}, f(x)>f _{100}(x)$ है। किंतु हम यहाँ पर इसकी उपपत्ति देने का प्रयास नहीं करेंगे। इसी प्रकार $x$ के बड़े मानों को चुनकर यह सत्यापित किया जा सकता है कि, किसी भी धन पूर्णांक $n$ के लिए $f _{n}(x)$ की अपेक्षा $f(x)$ का मान अधिक तेजी से बढ़ता है।
परिभाषा 3 फलन $y=f(x)=b^{x}$, धनात्मक आधार $b>1$ के लिए चरघातांकी फलन कहलाता है।
आकृति 5.9 में $y=10^{x}$ का रेखाचित्र दर्शाया गया है।
यह सलाह दी जाती है कि पाठक इस रेखाचित्र को $b$ के विशिष्ट मानों, जैसे 2,3 और 4 के लिए खींच कर देखें। चरघातांकी फलन की कुछ प्रमुख विशेषताएँ निम्नलिखित हैं:
(1) चरघातांकी फलन का प्रांत, वास्तविक संख्याओं का समुच्चय $\mathbf{R}$ होता है।
(2) चरघातांकी फलन का परिसर, समस्त धनात्मक वास्तविक संख्याओं का समुच्चय होता है।
(3) बिंदु $(0,1)$ चरघातांकी फलन के आलेख पर सदैव होता है (यह इस तथ्य का पुनः कथन है कि किसी भी वास्तविक संख्या $b>1$ के लिए $b^{0}=1$ )
(4) चरघातांकी फलन सदैव एक वर्धमान फलन (increasing function) होता है, अर्थात् जैसे-जैसे हम बाएँ से दाएँ ओर बढ़ते जाते हैं, आलेख ऊपर उठता जाता है।
(5) $x$ के अत्यधिक बड़े ऋणात्मक मानों के लिए चरघातांकी फलन का मान 0 के अत्यंत निकट होता है। दूसरे शब्दों में, द्वितीय चतुर्थांश में, आलेख उत्तरोत्तर $x$-अक्ष की ओर अग्रसर होता है ( किंतु उससे कभी मिलता नहीं है।)
आधार 10 वाले चरघातांकी फलन को साधारण चरघातांकी फलन (common exponential Function) कहते हैं। कक्षा XI की पाठ्यपुस्तक के परिशिष्ट A.1.4 में हमने देखा था कि श्रेणी
$$ 1+\frac{1}{1 !}+\frac{1}{2 !}+\ldots \text { है। } $$
का योग एक ऐसी संख्या है जिसका मान 2 तथा 3 के मध्य होता है और जिसे $e$ द्वारा प्रकट करते हैं। इस $e$ को आधार के रूप में प्रयोग करने पर, हमें एक अत्यंत महत्वपूर्ण चरघातांकी फलन $y=e^{x}$ प्राप्त होता है। इसे प्राकृतिक चरघातांकी फलन (natural exponential function) कहते हैं।
यह जानना रुचिकर होगा कि क्या चरघातांकी फलन के प्रतिलोम का अस्तित्व है और यदि ‘हाँ’ तो क्या उसकी एक समुचित व्याख्या की जा सकती है। यह खोज निम्नलिखित परिभाषा के लिए प्रेरित करती है।
परिभाषा 4 मान लीजिए कि $b>1$ एक वास्तविक संख्या है। तब हम कहते हैं कि, $b$ आधार पर $a$ का लघुगणक $x$ है,
यदि $b^{x}=a$ है। $b$ आधार पर $a$ के लघुगणक को प्रतीक $\log _{b} a$ से प्रकट करते हैं। इस प्रकार यदि $b^{x}=a$, तो $\log _{b} a=x$ इसका अनुभव करने के लिए आइए हम कुछ स्पष्ट उदाहरणों का प्रयोग करें। हमें ज्ञात है कि $2^{3}=8$ है। लघुगणकीय शब्दों में हम इसी बात को पुन: $\log _{2} 8=3$ लिख सकते हैं। इसी प्रकार $10^{4}=10000$ तथा $\log _{10} 10000=4$ समतुल्य कथन हैं। इसी तरह से $625=5^{4}=25^{2}$ तथा $\log _{5}$ $625=4$ अथवा $\log _{25} 625=2$ समतुल्य कथन हैं।
थोड़ा सा और अधिक परिपक्व दृष्टिकोण से विचार करने पर हम कह सकते हैं कि $b>1$ को आधार निर्धारित करने के कारण ‘लघुगणक’ को धन वास्तविक संख्याओं के समुच्चय से सभी वास्तविक संख्याओं के समुच्चय में एक फलन के रूप में देखा जा सकता है। यह फलन, जिसे लघुगणकीय फलन (logarithmic function) कहते हैं, निम्नलिखित प्रकार से परिभाषित है:
$$ \begin{aligned} \log _{b}: \mathbf{R}^{+} & \rightarrow \mathbf{R} \\ x & \rightarrow \log _{b} x=y \text { यदि } b^{y}=x \end{aligned} $$
पूर्व कथित तरह से, यदि आधार $b=10$ है तो इसे ‘साधारण लघुगणक’ और यदि $b=e$ है तो इसे ‘प्राकृतिक लघुगणक’ कहते हैं। बहुधा प्राकृतिक लघुगणक को $\ln$ द्वारा प्रकट करते हैं। इस अध्याय में $\log x$ आधार $e$ वाले लघुगणकीय फलन को निरूपित करता है। आकृति 5.10 में 2 , तथा 10 आधारीय लघुगणकीय फलनों के आलेख दर्शाए गए हैं।
आधार $b>1$ वाले लघुगणकीय फलनों की कुछ महत्वपूर्ण विशेषताएँ नीचे सूचीबद्ध हैं:

आकृति 5.10
(1) धनेतर (non-positive) संख्याओं के लिए हम लघुगणक की कोई अर्थपूर्ण परिभाषा नहीं बना सकते हैं और इसलिए लघुगणकीय फलन का प्रांत $\mathbf{R}^{+}$है।
(2) लघुगणकीय फलन का परिसर समस्त वास्तविक संख्याओं का समुच्चय है।
(3) बिंदु $(1,0)$ लघुगणकीय फलनों के आलेख पर सदैव रहता है।
(4) लघुगणकीय फलन एक वर्धमान फलन होते हैं, अर्थात् ज्यों-ज्यों हम बाएँ से दाएँ ओर चलते हैं, आलेख उत्तरोत्तर ऊपर उठता जाता है।
(5) 0 के अत्याधिक निकट वाले $x$ के लिए, $\log x$ के मान को किसी भी दी गई वास्तविक संख्या से कम किया जा सकता है। दूसरे शब्दों में, चौथे (चतुर्थ) चतुर्थांश में आलेख $y$-अक्ष के निकटतम अग्रसर होता है (किंतु इससे कभी मिलता नहीं है)।
(6) आकृति 5.11 में $y=e^{x}$ तथा $y=\log _{e} x$ के आलेख दर्शाए गए हैं। यह ध्यान देना रोचक है कि दोनों वक्र रेखा $y=x$ में एक दूसरे के दर्पण प्रतिबिंब हैं।

आकृति 5.11
लघुगणकीय फलनों के दो महत्वपूर्ण गुण नीचे प्रमाणित किए गए हैं:
(1) आधार परिवर्तन का एक मानक नियम है, जिससे $\log _{a} p$ को $\log _{b} p$ के पदों में ज्ञात किया जा सकता है। मान लीजिए कि $\log _{a} p=\alpha, \log _{b} p=\beta$ तथा $\log _{b} a=\gamma$ है। इसका अर्थ यह है कि $a^{\alpha}=p, b^{\beta}=p$ तथा $b^{\gamma}=a$ है।
अब तीसरे परिणाम को पहले में रखने से
$$ \left(b^{\gamma}\right)^{\alpha}=b^{\gamma \alpha}=p $$
इसको दूसरे समीकरण में प्रयोग करने पर
$$ \begin{aligned} b^{\beta} & =p=b^{\gamma \alpha} \\ \beta & =\alpha \gamma \text { अथवा } \alpha=\frac{\beta}{\gamma} \text { है। इस प्रकार } \\ \log _{a} p & =\frac{\log _{b} p}{\log _{b} a} \end{aligned} $$
(2) गुणनफलनों पर $\log$ फलन का प्रभाव इसका एक अन्य रोचक गुण है। मान लीजिए कि $\log _{b} p q=\alpha$ है। इससे $b^{\alpha}=p q$ प्राप्त होता है। इसी प्रकार यदि $\log _{b} p=\beta$ तथा $\log _{b} q=\gamma$ है तो $b^{\beta}=p$ तथा $b^{\gamma}=q$ प्राप्त होता है। परंतु $b^{\alpha}=p q=b^{\beta} b^{\gamma}=b^{\beta+\gamma}$ है।
इसका तात्पर्य है कि $\alpha=\beta+\gamma$,अर्थात्
$$ \log _{b} p q=\log _{b} p+\log _{b} q $$
इससे एक विशेष रोचक तथा महत्वपूर्ण परिणाम तब निकलता है जब $p=q$ है। ऐसी दशा में, उपर्युक्त को पुनः निम्नलिखित प्रकार से लिखा जा सकता है
$$ \log _{b} p^{2}=\log _{b} p+\log _{b} p=2 \log _{b} p $$
इसका एक सरल व्यापकीकरण अभ्यास के लिए छोड़ दिया गया है अर्थात् किसी भी धन पूर्णांक $n$ के लिए
$$ \log _{b} p^{n}=n \log _{b} p $$
वास्तव में यह परिणाम $n$ के किसी भी वास्तविक मान के लिए सत्य है, किंतु इसे हम प्रमाणित करने का प्रयास नहीं करेंगे। इसी विधि से पाठक निम्नलिखित को सत्यापित कर सकते हैं:
$$ \log _{b} \frac{x}{y}=\log _{b} x-\log _{b} y $$
उदाहरण 24 क्या यह सत्य है कि $x$ के सभी वास्तविक मानों के लिए $x=e^{\log x}$ है?
हल पहले तो ध्यान दीजिए कि $\log$ फलन का प्रांत सभी धन वास्तविक संख्याओं का समुच्चय होता है। इसलिए उपर्युक्त समीकरण धनेतर वास्तविक संख्याओं के लिए सत्य नहीं है। अब मान लीजिए कि $y=e^{\log x}$ है। यदि $y>0$ तब दोनो पक्षों का लघुगणक लेने से $\log y=\log \left(e^{\log x}\right)=\log x \cdot \log$ $e=\log x$ है। जिससे $y=x$ प्राप्त होता है। अतएव $x=e^{\log x}$ केवल $x$ के धन मानों के लिए सत्य है।
अवकल गणित (differential calculus) में, प्राकृतिक चरघातांकी फलन का एक असाधारण गुण यह है कि, अवकलन की प्रक्रिया में यह परिवर्तित नहीं होता है। इस गुण को नीचे प्रमेयों में व्यक्त किया गया है, जिसकी उपपत्ति को हम छोड़ देते हैं।
प्रमेय 5
(1) $x$ के सापेक्ष $e^{x}$ का अवकलज $e^{x}$ ही होता है, अर्थात् $\frac{d}{d x}\left(e^{x}\right)=e^{x}$
(2) $x$ के सापेक्ष $\log x$ का अवकलज $\frac{1}{x}$ होता है, अर्थात् $\frac{d}{d x}(\log x)=\frac{1}{x}$
उदाहरण $25 x$ के सापेक्ष निम्नलिखित का अवकलन कीजिए:
(i) $e^{-x}$
(ii) $\sin (\log x), x>0$
(iii) $\cos ^{-1}\left(e^{x}\right)$
(iv) $e^{\cos x}$
हल
(i) मान लीजिए $y=e^{-x}$ है। अब श्रंखला नियम के प्रयोग द्वारा
$$ \frac{d y}{d x}=e^{-x} \cdot \frac{d}{d x}(-x)=-e^{-x} $$
(ii) मान लीजिए कि $y=\sin (\log x)$ है। अब शृंखला नियम द्वारा
$$ \frac{d y}{d x}=\cos (\log x) \cdot \frac{d}{d x}(\log x)=\frac{\cos (\log x)}{x} $$
(iii) मान लीजिए कि $y=\cos ^{-1}\left(e^{x}\right)$ है। अब शृंखला नियम द्वारा
$$ \frac{d y}{d x}=\frac{-1}{\sqrt{1-\left(e^{x}\right)^{2}}} \cdot \frac{d}{d x}\left(e^{x}\right)=\frac{-e^{x}}{\sqrt{1-e^{2 x}}} . $$
(iv) मान लीजिए कि $y=e^{\cos x}$ है। अब शृंखला नियम द्वारा
$$ \frac{d y}{d x}=e^{\cos x} \cdot(-\sin x)=-(\sin x) e^{\cos x} $$[^0]
प्रश्नावली 5.4
निम्नलिखित का $x$ के सापेक्ष अवकलन कीजिए:
1. $\frac{e^{x}}{\sin x}$
Show Answer
#missing2. $e^{\sin ^{-1} x}$
Show Answer
#missing3. $e^{x^{3}}$
Show Answer
#missing4. $\sin \left(\tan ^{-1} e^{-x}\right)$
Show Answer
#missing5. $\log \left(\cos e^{x}\right)$
Show Answer
#missing6. $e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}$
Show Answer
#missing7. $\sqrt{e^{\sqrt{x}}}, x>0$
Show Answer
#missing8. $\log (\log x), x>1$
Show Answer
#missing9. $\frac{\cos x}{\log x}, x>0$
Show Answer
#missing10. $\cos \left(\log x+e^{x}\right)$
Show Answer
#missing5.5. लघुगणकीय अवकलन (Logarithmic Differentiation)
इस अनुच्छेद में हम निम्नलिखित प्रकार के एक विशिष्ट वर्ग के फलनों का अवकलन करना सीखेंगे:
$$ y=f(x)=[u(x)]^{v(x)} $$
लघुगणक ( $e$ आधार पर $)$ लेने पर उपर्युक्त को निम्नलिखित प्रकार से पुनः लिख सकते हैं
$$ \log y=v(x) \log [u(x)] $$
शृंखला नियम के प्रयोग द्वारा
$$ \frac{1}{y} \cdot \frac{d y}{d x}=v(x) \cdot \frac{1}{u(x)} \cdot u^{\prime}(x)+v^{\prime}(x) \cdot \log [u(x)] $$
इसका तात्पर्य है कि
$$ \frac{d y}{d x}=y\left[\frac{v(x)}{u(x)} \cdot u^{\prime}(x)+v^{\prime}(x) \cdot \log [u(x)]\right] $$
इस विधि में ध्यान देने की मुख्य बात यह है कि $f(x)$ तथा $u(x)$ को सदैव धनात्मक होना चाहिए अन्यथा उनके लघुगणक परिभाषित नहीं होंगे। इस प्रक्रिया को लघुगणकीय अवकलन (logarithmic differentiation) कहते हैं और जिसे निम्नलिखित उदाहरणों द्वारा स्पष्ट किया गया है।
उदाहरण 26 $x$ के सापेक्ष $\sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}$ का अवकलन कीजिए।
हल मान लीजिए कि $y=\sqrt{\frac{(x-3)\left(x^{2}+4\right)}{\left(3 x^{2}+4 x+5\right)}}$
दोनों पक्षों के लघुगणक लेने पर
$$ \log y=\frac{1}{2}\left[\log (x-3)+\log \left(x^{2}+4\right)-\log \left(3 x^{2}+4 x+5\right)\right] $$
दोनों पक्षों का $x$, के सापेक्ष अवलकन करने पर
$$ \frac{1}{y} \cdot \frac{d y}{d x}=\frac{1}{2}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right] $$
अथवा $\qquad\frac{d y}{d x}=\frac{y}{2}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right]$
$$ =\frac{1}{2} \sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}\left[\frac{1}{(x-3)}+\frac{2 x}{x^{2}+4}-\frac{6 x+4}{3 x^{2}+4 x+5}\right] $$
उदाहरण 27 $x$ के सापेक्ष $a^{x}$ का अवकलन कीजिए, जहाँ $a$ एक धन अचर है।
हल मान लीजिए कि $y=a^{x}$, तो
$$ \log y=x \log a $$
दोनों पक्षों का $x$, के सापेक्ष अवकलन करने पर
$ \begin{aligned} & \frac{1}{y} \frac{d y}{d x}=\log a \\ \text{ अथवा } \qquad & \frac{d y}{d x}=y \log a \\ \text{ इस प्रकार } \qquad & \frac{d}{d x}\left(a^x\right)=a^x \log a \\ \text { विकल्पत: } \qquad & \frac{d}{d x}\left(a^x\right) =\frac{d}{d x}\left(e^{x \log a}\right)=e^{x \log a} \frac{d}{d x}(x \log a) \\ & =e^{x \log a} \cdot \log a=a^x \log a \end{aligned} $
उदाहरण 28 $x$ के सापेक्ष $x^{\sin x}$, का अवकलन कीजिए, जब कि $x>0$ है।
हल मान लीजिए कि $y=x^{\sin x}$ है। अब दोनों पक्षों का लघुगणक लेने पर
$$ \begin{aligned} \log y & =\sin x \log x \\ \frac{1}{y} \cdot \frac{d y}{d x} & =\sin x \frac{d}{d x}(\log x)+\log x \frac{d}{d x}(\sin x) \end{aligned} $$
अतएव $\qquad \frac{1}{y} \frac{d y}{d x}=(\sin x) \frac{1}{x}+\log x \cos x$
या $\qquad \begin{aligned}\frac{d y}{d x} & =y[\frac{\sin x}{x}+\cos x \log x] \& =x^{\sin x}[\frac{\sin x}{x}+\cos x \log x] \& =x^{\sin x-1} \cdot \sin x+x^{\sin x} \cdot \cos x \log x\end{aligned}$
उदाहरण 29 यदि $y^{x}+x^{y}+x^{x}=a^{b}$ है। तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल दिया है कि $y^{x}+x^{y}+x^{x}=a^{b}$
$u=y^{x}, v=x^{y}$ तथा $w=x^{x}$ रखने पर हमें $u+v+w=a^{b}$ प्राप्त होता है।
इसलिए $\quad \frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}=0 \qquad \qquad (1) $
अब $u=y^{x}$ है। दोनों पक्षों का लघुगणक लेने पर
$$ \log u=x \log y $$
दोनों पक्षों का $x$ के सापेक्ष अवकलन करने पर
$$ \begin{aligned} \frac{1}{u} \cdot \frac{d u}{d x} & =x \frac{d}{d x}(\log y)+\log y \frac{d}{d x}(x) \\ & =x \frac{1}{y} \cdot \frac{d y}{d x}+\log y \cdot 1 \text { प्राप्त होता है। } \\ \text{ इसलिए } \qquad \qquad \frac{d u}{d x} & =u(\frac{x}{y} \frac{d y}{d x}+\log y)=y^{x}[\frac{x}{y} \frac{d y}{d x}+\log y] \qquad \qquad (2) \end{aligned} $$
इसी प्रकार $v=x^{y} $
दोनों पक्षों का लघुगणक लेने पर
$$ \log v=y \log x $$
दोनों पक्षों का $x$ के सापेक्ष अवकलन करने पर
$$ \begin{aligned} \frac{1}{v} \cdot \frac{d v}{d x} & =y \frac{d}{d x}(\log x)+\log x \frac{d y}{d x} \\ & =y \cdot \frac{1}{x}+\log x \cdot \frac{d y}{d x} \\ \text{ अतएव } \qquad \qquad \frac{d v}{d x} & =v[\frac{y}{x}+\log x \frac{d y}{d x}] \\ & =x^{y}[\frac{y}{x}+\log x \frac{d y}{d x}] \qquad \qquad (3) \end{aligned} $$
पुन: $ \qquad \qquad w=x^{x} $
दोनों पक्षों का लघुगणन करने पर
$$ \log w=x \log x $$
दोनों पक्षों का $x$ के सापेक्ष अवकलन करने पर
$$ \begin{aligned} \frac{1}{w} \cdot \frac{d w}{d x} & =x \frac{d}{d x}(\log x)+\log x \cdot \frac{d}{d x}(x) \\ & =x \cdot \frac{1}{x}+\log x \cdot 1 \text { प्राप्त होता है। } \end{aligned} $$
$$ \begin{aligned} \text{ अर्थात् } \qquad \qquad \frac{d w}{d x} & =w(1+\log x) \\ & =x^{x}(1+\log x) \qquad \qquad (4) \end{aligned} $$
(1), (2), (3) तथा (4), द्वारा
$ y^{x}\left(\frac{x}{y} \frac{d y}{d x}+\log y\right)+x^{y}\left(\frac{y}{x}+\log x \frac{d y}{d x}\right)+x^{x}(1+\log x)=0 $
या $\left(x \cdot y^{x-1}+x^{y} \cdot \log x\right) \frac{d y}{d x}=-x^{x}(1+\log x)-y \cdot x^{y-1}-y^{x} \log y$
अत: $\qquad\frac{d y}{d x}=\frac{-\left[y^{x} \log y+y \cdot x^{y-1}+x^{x}(1+\log x)\right]}{x \cdot y^{x-1}+x^{y} \log x}$
प्रश्नावली 5.5
1 से 11 तक के प्रश्नों में प्रदत्त फलनों का $x$ के सापेक्ष अवकलन कीजिए:
1. $\cos x \cdot \cos 2 x \cdot \cos 3 x$
Show Answer
#missing2. $\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}$
Show Answer
#missing3. $(\log x)^{\cos x}$
Show Answer
#missing4. $x^{x}-2^{\sin x}$
Show Answer
#missing5. $(x+3)^{2} \cdot(x+4)^{3} \cdot(x+5)^{4}$
Show Answer
#missing6. $\left(x+\frac{1}{x}\right)^{x}+x^{\left(1+\frac{1}{x}\right)}$
Show Answer
#missing7. $(\log x)^{x}+x^{\log x}$
Show Answer
#missing8. $(\sin x)^{x}+\sin ^{-1} \sqrt{x}$
Show Answer
#missing9. $x^{\sin x}+(\sin x)^{\cos x}$
Show Answer
#missing10. $x^{x \cos x}+\frac{x^{2}+1}{x^{2}-1}$
Show Answer
#missing11. $(x \cos x)^{x}+(x \sin x)^{\frac{1}{x}}$
Show Answer
#missing12 से 15 तक के प्रश्नों में प्रदत्त फलनों के लिए $\frac{d y}{d x}$ ज्ञात कीजिए:
12. $x^{y}+y^{x}=1$
Show Answer
#missing13. $y^{x}=x^{y}$
Show Answer
#missing14. $(\cos x)^{y}=(\cos y)^{x}$
Show Answer
#missing15. $x y=e^{(x-y)}$
Show Answer
#missing16. $f(x)=(1+x)\left(1+x^{2}\right)\left(1+x^{4}\right)\left(1+x^{8}\right)$ द्वारा प्रदत्त फलन का अवकलज ज्ञात कीजिए और इस प्रकार $f^{\prime}$ (1) ज्ञात कीजिए।
Show Answer
#missing17. $\left(x^{2}-5 x+8\right)\left(x^{3}+7 x+9\right)$ का अवकलन निम्नलिखित तीन प्रकार से कीजिए:
(i) गुणनफल नियम का प्रयोग करके
(ii) गुणनफल के विस्तारण द्वारा एक एकल बहुपद प्राप्त करके
(iii) लघुगणकीय अवकलन द्वारा
यह भी सत्यापित कीजिए कि इस प्रकार प्राप्त तीनों उत्तर समान हैं।
Show Answer
#missing18. यदि $u, v$ तथा $w, x$ के फलन हैं, तो दो विधियों अर्थात् प्रथम-गुणनफल नियम की पुनरावृत्ति द्वारा, द्वितीय - लघुगणकीय अवकलन द्वारा दर्शाइए कि
$$ \frac{d}{d x}(u \cdot v \cdot w)=\frac{d u}{d x} v \cdot w+u \cdot \frac{d v}{d x} \cdot w+u \cdot v \frac{d w}{d x} $$
Show Answer
#missing5.6 फलनों के प्राचलिक रूपों के अवकलज (Derivatives of Functions in Parametric Forms)
कभी-कभी दो चर राशियों के बीच का संबंध न तो स्पष्ट होता है और न अस्पष्ट, किंतु एक अन्य ( तीसरी) चर राशि से पृथक्-पृथक् संबंधों द्वारा प्रथम दो राशियों के मध्य एक संबंध स्थापित हो जाता है ऐसी स्थिति में हम कहते हैं कि उन दोनों के बीच का संबंध एक तीसरी चर राशि के माध्यम से वर्णित है। यह तीसरी चर राशि प्राचल (Parameter) कहलाती है। अधिक सुस्पष्ट तरीके से दो चर राशियों $x$ तथा $y$ के बीच, $x=f(t), y=g(t)$ के रूप में व्यक्त संबंध, को प्राचलिक रूप में व्यक्त संबंध कहते हैं, जहाँ $t$ एक प्राचल है।
इस रूप के फलनों के अवकलज ज्ञात करने हेतु, शृंखला नियम द्वारा
$$ \begin{aligned} & \frac{d y}{d t}=\frac{d y}{d x} \cdot \frac{d x}{d t} \\ \end{aligned} $$
इस प्रकार $\qquad \frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\left(\text { जब कभी }\frac{d x}{d t} \neq 0\right) \text { प्राप्त होता है। }$
$$ \frac{d y}{d x}=\frac{g^{\prime}(t)}{f^{\prime}(t)}\left(\text { क्योंकि } \frac{d y}{d t}=g^{\prime}(t) \text { तथा } \frac{d x}{d t}=f^{\prime}(t)\right)\left[\text { बशर्ते } f^{\prime}(t) \neq 0\right] $$
उदाहरण 30 यदि $x=a \cos \theta, y=a \sin \theta$, तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल दिया है कि
$$ x=a \cos \theta, y=a \sin \theta $$
इसलिए $\quad \frac{d x}{d \theta}=-a \sin \theta, \frac{d y}{d \theta}=a \cos \theta$
अत: $\quad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{a \cos \theta}{-a \sin \theta}=-\cot \theta$
उदाहरण 31 यदि $x=a t^{2}, y=2 a t$ है तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल दिया है कि $x=a t^{2}, y=2 a t$
इसलिए $ \qquad\frac{d x}{d t}=2 a t \text { तथा } \frac{d y}{d t}=2 a$
अत: $ \qquad \frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{2 a}{2 a t}=\frac{1}{t}$
उदाहरण 32 यदि $x=a(\theta+\sin \theta), y=a(1-\cos \theta)$ है तो $\frac{d y}{d x}$ ज्ञात कीजिए ।
हल यहाँ $\frac{d x}{d \theta}=a(1+\cos \theta), \frac{d y}{d \theta}=a(\sin \theta)$
अतः $\qquad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{a \sin\theta}{a(1+\cos \theta)}=\tan \frac{\theta}{2}$
टिप्पणी यहाँ, यह ध्यान दीजिए कि $\frac{d y}{d x}$ को मुख्य चर राशियों $x$ और $y$ को सम्मिलित किए बिना ही, केवल प्राचल के पदों में व्यक्त करते हैं।
उदाहरण 33 यदि $x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$ है तो $\frac{d y}{d x}$ ज्ञात कीजिए।
हल मान लीजिए कि $x=a \cos ^{3} \theta, y=a \sin ^{3} \theta$ है तब
$$ \begin{aligned} x^{\frac{2}{3}}+y^{\frac{3}{2}} & =\left(a \cos ^{3} \theta\right)^{\frac{2}{3}}+\left(a \sin ^{3} \theta\right)^{\frac{2}{3}} \\ & =a^{\frac{2}{3}}\left(\cos ^{2} \theta+\left(\sin ^{2} \theta\right)=a^{\frac{2}{3}}\right. \end{aligned} $$
अतः$x=a \cos ^{3} \theta, y=a \sin ^{3} \theta, x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$ का प्राचलिक समीकरण है।
इस प्रकार, $\qquad \frac{d x}{d \theta}=-3 a \cos ^{2} \theta \sin \theta$ और $\frac{d y}{d \theta}=3 a \sin ^{2} \theta \cos \theta$
इसलिए, $\quad \frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{3 a \sin ^{2} \theta \cos \theta}{-3 a \cos ^{2} \theta \sin \theta}=-\tan \theta=-\sqrt[3]{\frac{y}{x}}$
प्रश्नावली 5.6
यदि प्रश्न संख्या 1 से 10 तक में $x$ तथा $y$ दिए समीकरणों द्वारा, एक दूसरे से प्राचलिक रूप में संबंधित हों, तो प्राचलों का विलोपन किए बिना, $\frac{d y}{d x}$ ज्ञात कीजिए:
1. $x=2 a t^{2}, y=a t^{4}$
Show Answer
#missing2. $x=a \cos \theta, y=b \cos \theta$
Show Answer
#missing3. $x=\sin t, y=\cos 2 t$
Show Answer
#missing4. $x=4 t, y=\frac{4}{t}$
Show Answer
#missing5. $x=\cos \theta-\cos 2 \theta, y=\sin \theta-\sin 2 \theta$
Show Answer
#missing6. $x=a(\theta-\sin \theta), y=a(1+\cos \theta)$
Show Answer
#missing7. $x=\frac{\sin ^{3} t}{\sqrt{\cos 2 t}}, y=\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}$
Show Answer
#missing8. $x=a\left(\cos t+\log \tan \frac{t}{2}\right) y=a \sin t$
Show Answer
#missing9. $x=a \sec \theta, y=b \tan \theta$
Show Answer
#missing10. $x=a(\cos \theta+\theta \sin \theta), y=a(\sin \theta-\theta \cos \theta)$
Show Answer
#missing11. यदि $x=\sqrt{a^{\sin ^{-1} t}}, y=\sqrt{a^{\cos ^{-1} t}}$, तो दर्शाइए कि $\frac{d y}{d x}=-\frac{y}{x}$
Show Answer
#missing5.7 द्वितीय कोटि का अवकलज (Second Order Derivative)
$$ \begin{align*} \text {मान लीजिए कि } \qquad y & =f(x) \text { है तो } \\ \frac{d y}{d x} & =f^{\prime}(x) \tag{1} \end{align*} $$
यदि $f^{\prime}(x)$ अवकलनीय है तो हम $x$ के सापेक्ष (1) का पुनः अवकलन कर सकते हैं। इस प्रकार बायाँ पक्ष $\frac{d}{d x}\left(\frac{d y}{d x}\right)$ हो जाता है, जिसे द्वितीय कोटि का अवकलज (Second Order Derviative) कहते हैं और $\frac{d^{2} y}{d x^{2}}$ से निरूपित करते हैं। $f(x)$ के द्वितीय कोटि के अवकलज को $f^{\prime \prime}(x)$ से भी निरूपित करते हैं। यदि $y=f(x)$ हो तो इसे $\mathrm{D}^{2}(y)$ या $y^{\prime \prime}$ या $y _{2}$ से भी निरूपित करते हैं। हम टिप्पणी करते हैं कि उच्च क्रम के अवकलन भी इसी प्रकार किए जाते हैं।
उदाहरण 34 यदि $y=x^{3}+\tan x$ है तो $\frac{d^{2} y}{d x^{2}}$ ज्ञात कीजिए।
हल दिया है कि $y=x^{3}+\tan x$ है। अब
इसलिए $\qquad \begin{aligned}\frac{d y}{d x} & =3 x^{2}+\sec ^{2} x \\ \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}\left(3 x^{2}+\sec ^{2} x\right) \\ & =6 x+2 \sec x \cdot \sec x \tan x=6 x+2 \sec ^{2} x \tan x\end{aligned}$
उदाहरण 35 यदि $y=\mathrm{A} \sin x+\mathrm{B} \cos x$ है तो सिद्ध कीजिए कि $\frac{d^{2} y}{d x^{2}}+y=0$ है।
हल यहाँ पर
$$ \begin{aligned} & \frac{d y}{d x}=\mathrm{A} \cos x-\mathrm{B} \sin x \\ \text{ और } \qquad & \frac{d^2 y}{d x^2} =\frac{d}{d x}(\mathrm{~A} \cos x-\mathrm{B} \sin x) \\ & \qquad =-\mathrm{A} \sin x-\mathrm{B} \cos x=-y \\ \text{ इस प्रकार } \qquad & \frac{d^2 y}{d x^2}+y=0 \end{aligned} $$
उदाहरण 36 यदि $y=3 e^{2 x}+2 e^{3 x}$ है तो सिद्ध कीजिए कि $\frac{d^{2} y}{d x^{2}}-5 \frac{d y}{d x}+6 y=0$
हल यहाँ $y=3 e^{2 x}+2 e^{3 x}$ है। अब
इसलिए $\qquad \frac{d y}{d x}=6 e^{2 x}+6 e^{3 x}=6\left(e^{2 x}+e^{3 x}\right)$
अत: $\qquad \frac{d^{2} y}{d x^{2}}=12 e^{2 x}+18 e^{3 x}=6\left(2 e^{2 x}+3 e^{3 x}\right)$
$$ \frac{d^{2} y}{d x^{2}}-5 \frac{d y}{d x}+6 y=6\left(2 e^{2 x}+3 e^{3 x}\right) $$
$$ -30\left(e^{2 x}+e^{3 x}\right)+6\left(3 e^{2 x}+2 e^{3 x}\right)=0 $$
उदाहरण 37 यदि $y=\sin ^{-1} x$ है तो दर्शाइए कि $\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=0$ है।
हल यहाँ $y=\sin ^{-1} x$ है तो
या $\qquad \frac{d y}{d x}=\frac{1}{\sqrt{\left(1-x^{2}\right)}}$
$$ \sqrt{\left(1-x^{2}\right)} \frac{d y}{d x}=1 $$
या $\qquad\frac{d}{d x}\left(\sqrt{\left(1-x^{2}\right)} \cdot \frac{d y}{d x}\right)=0$
या $\qquad\sqrt{\left(1-x^{2}\right)} \cdot \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot \frac{d}{d x}\left(\sqrt{\left(1-x^{2}\right)}\right)=0$
$\qquad\begin{aligned}\text {या } \qquad & \sqrt{\left(1-x^{2}\right)} \cdot \frac{d^{2} y}{d x{2}}-\frac{d y}{d x} \cdot \frac{2 x}{2 \sqrt{1-x^{2}}}=0 \\ & \left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}=0\end{aligned}$
विकल्पत: दिया है कि $y=\sin ^{-1} x$ है तो
$$ y _{1}=\frac{1}{\sqrt{1-x^{2}}}, \text { अर्थात् }\left(1-x^{2}\right) y _{1}^{2}=1 $$
अतएव $\qquad \left(1-x^{2}\right) \cdot 2 y _{1} y _{2}+y _{1}^{2}(0-2 x)=0$
अतः $\qquad \left(1-x^{2}\right) y _{2}-x y _{1}=0$
प्रश्नावली 5.7
प्रश्न संख्या 1 से 10 तक में दिए फलनों के द्वितीय कोटि के अवकलज ज्ञात कीजिए:
1. $x^{2}+3 x+2$
Show Answer
समाधान
होने देना $y=x^{2}+3 x+2$
तब,
$\frac{d y}{d x}=\frac{d}{d x}(x^{2})+\frac{d}{d x}(3 x)+\frac{d}{d x}(2)=2 x+3+0=2 x+3$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(2 x+3)=\frac{d}{d x}(2 x)+\frac{d}{d x}(3)=2+0=2$
2. $x^{20}$
Show Answer
समाधान
होने देना $y=x^{20}$
तब,
$\frac{d y}{d x}=\frac{d}{d x}(x^{20})=20 x^{19}$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(20 x^{19})=20 \frac{d}{d x}(x^{19})=20 \cdot 19 \cdot x^{18}=380 x^{18}$
3. $x \cdot \cos x$
Show Answer
समाधान
होने देना $y=x \cdot \cos x$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(x \cdot \cos x)=\cos x \cdot \frac{d}{d x}(x)+x \frac{d}{d x}(\cos x)=\cos x \cdot 1+x(-\sin x)=\cos x-x \sin x \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[\cos x-x \sin x]=\frac{d}{d x}(\cos x)-\frac{d}{d x}(x \sin x) \\ & =-\sin x-[\sin x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\sin x)] \\ & =-\sin x-(\sin x+x \cos x) \\ & =-(x \cos x+2 \sin x) \end{aligned} \end{aligned} $
4. $\log x$
Show Answer
समाधान
होने देना $y=\log x$
तब,
$\frac{d y}{d x}=\frac{d}{d x}(\log x)=\frac{1}{x}$
$\therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(\frac{1}{x})=\frac{-1}{x^{2}}$
5. $x^{3} \log x$
Show Answer
समाधान
होने देना $y=x^{3} \log x$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[x^{3} \log x]=\log x \cdot \frac{d}{d x}(x^{3})+x^{3} \cdot \frac{d}{d x}(\log x) \\ & =\log x \cdot 3 x^{2}+x^{3} \cdot \frac{1}{x}=\log x \cdot 3 x^{2}+x^{2} \\ & =x^{2}(1+3 \log x) \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[x^{2}(1+3 \log x)] \\ & =(1+3 \log x) \cdot \frac{d}{d x}(x^{2})+x^{2} \frac{d}{d x}(1+3 \log x) \\ & =(1+3 \log x) \cdot 2 x+x^{2} \cdot \frac{3}{x} \\ & =2 x+6 x \log x+3 x \\ & =5 x+6 x \log x \\ & =x(5+6 \log x) \end{aligned} $
6. $e^{x} \sin 5 x$
Show Answer
समाधान
होने देना $y=e^{x} \sin 5 x$
तब
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}(e^{x} \sin 5 x)=\sin 5 x \cdot \frac{d}{d x}(e^{x})+e^{x} \frac{d}{d x}(\sin 5 x) \\ & =\sin 5 x \cdot e^{x}+e^{x} \cdot \cos 5 x \cdot \frac{d}{d x}(5 x)=e^{x} \sin 5 x+e^{x} \cos 5 x \cdot 5 \\ & =e^{x}(\sin 5 x+5 \cos 5 x) \\ \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[e^{x}(\sin 5 x+5 \cos 5 x)] \\ & =(\sin 5 x+5 \cos 5 x) \cdot \frac{d}{d x}(e^{x})+e^{x} \cdot \frac{d}{d x}(\sin 5 x+5 \cos 5 x) \\ & =(\sin 5 x+5 \cos 5 x) e^{x}+e^{x}[\cos 5 x \cdot \frac{d}{d x}(5 x)+5(-\sin 5 x) \cdot \frac{d}{d x}(5 x)] \\ & =e^{x}(\sin 5 x+5 \cos 5 x)+e^{x}(5 \cos 5 x-25 \sin 5 x) \\ & =e^{x}(10 \cos 5 x-24 \sin 5 x)=2 e^{x}(5 \cos 5 x-12 \sin 5 x) \end{aligned} $
7. $e^{6 x} \cos 3 x$
Show Answer
समाधान
होने देना $y=e^{6 x} \cos 3 x$
तब,
$ \begin{aligned} \frac{d y}{d x} & =\frac{d}{d x}(e^{6 x} \cdot \cos 3 x)=\cos 3 x \cdot \frac{d}{d x}(e^{6 x})+e^{6 x} \cdot \frac{d}{d x}(\cos 3 x) \\ & =\cos 3 x \cdot e^{6 x} \cdot \frac{d}{d x}(6 x)+e^{6 x} \cdot(-\sin 3 x) \cdot \frac{d}{d x}(3 x) \\ & =6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x \\ \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}(6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x)=6 \cdot \frac{d}{d x}(e^{6 x} \cos 3 x)-3 \cdot \frac{d}{d x}(e^{6 x} \sin 3 x) \\ & =6 \cdot[6 e^{6 x} \cos 3 x-3 e^{6 x} \sin 3 x]-3 \cdot[\sin 3 x \cdot \frac{d}{d x}(e^{6 x})+e^{6 x} \cdot \frac{d}{d x}(\sin 3 x)] \\ & =36 e^{6 x} \cos 3 x-18 e^{6 x} \sin 3 x-3[\sin 3 x \cdot e^{6 x} \cdot 6+e^{6 x} \cdot \cos 3 x \cdot 3] \\ & =36 e^{6 x} \cos 3 x-18 e^{6 x} \sin 3 x-18 e^{6 x} \sin 3 x-9 e^{6 x} \cos 3 x \\ & =27 e^{6 x} \cos 3 x-36 e^{6 x} \sin 3 x \\ & =9 e^{6 x}(3 \cos 3 x-4 \sin 3 x) \end{aligned} $
8. $\tan ^{-1} x$
Show Answer
समाधान
होने देना $y=\tan ^{-1} x$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(\tan ^{-1} x)=\frac{1}{1+x^{2}} \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(\frac{1}{1+x^{2}})=\frac{d}{d x}(1+x^{2})^{-1}=(-1) \cdot(1+x^{2})^{-2} \cdot \frac{d}{d x}(1+x^{2}) \\ & \quad=\frac{-1}{(1+x^{2})^{2}} \times 2 x=\frac{-2 x}{(1+x^{2})^{2}} \end{aligned} $
9. $\log (\log x)$
Show Answer
समाधान
होने देना $y=\log (\log x)$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[\log (\log x)]=\frac{1}{\log x} \cdot \frac{d}{d x}(\log x)=\frac{1}{x \log x}=(x \log x)^{-1} \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[(x \log x)^{-1}]=(-1) \cdot(x \log x)^{-2} \cdot \frac{d}{d x}(x \log x) \\ & =\frac{-1}{(x \log x)^{2}} \cdot[\log x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log x)] \\ & =\frac{-1}{(x \log x)^{2}} \cdot[\log x \cdot 1+x \cdot \frac{1}{x}]=\frac{-(1+\log x)}{(x \log x)^{2}} \end{aligned} \end{aligned} $
10. $\sin (\log x)$
Show Answer
समाधान
होने देना $y=\sin (\log x)$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}[\sin (\log x)]=\cos (\log x) \cdot \frac{d}{d x}(\log x)=\frac{\cos (\log x)}{x} \\ & \begin{aligned} \therefore \frac{d^{2} y}{d x^{2}} & =\frac{d}{d x}[\frac{\cos (\log x)}{x}] \\ & =\frac{x \cdot \frac{d}{d x}[\cos (\log x)]-\cos (\log x) \cdot \frac{d}{d x}(x)}{x^{2}} \\ & =\frac{x \cdot[-\sin (\log x) \cdot \frac{d}{d x}(\log x)]-\cos (\log x) \cdot 1}{x^{2}} \\ & =\frac{-x \sin (\log x) \cdot \frac{1}{x}-\cos (\log x)}{x^{2}} \\ & =\frac{-[\sin (\log x)+\cos (\log x)]}{x^{2}} \end{aligned} \end{aligned} $
11. यदि $y=5 \cos x-3 \sin x$ है तो सिद्ध कीजिए कि $\frac{d^{2} y}{d x^{2}}+y=0$
Show Answer
समाधान
यह दिया गया है, $y=5 \cos x-3 \sin x$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(5 \cos x)-\frac{d}{d x}(3 \sin x)=5 \frac{d}{d x}(\cos x)-3 \frac{d}{d x}(\sin x) \\ & =5(-\sin x)-3 \cos x=-(5 \sin x+3 \cos x) \\ & \therefore \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[-(5 \sin x+3 \cos x)] \\ & =-[5 \cdot \frac{d}{d x}(\sin x)+3 \cdot \frac{d}{d x}(\cos x)] \\ & =-[5 \cos x+3(-\sin x)] \\ & =-[5 \cos x-3 \sin x] \\ & =-y \\ & \therefore \frac{d^{2} y}{d x^{2}}+y=0 \end{aligned} $
अत: सिद्ध हुआ।
12. यदि $y=\cos ^{-1} x$ है तो $\frac{d^{2} y}{d x^{2}}$ को केवल $y$ के पदों में ज्ञात कीजिए।
Show Answer
समाधान
यह दिया गया है, $y=\cos ^{-1} x$
तब,
$ \begin{aligned} & \frac{d y}{d x}=\frac{d}{d x}(\cos ^{-1} x)=\frac{-1}{\sqrt{1-x^{2}}}=-(1-x^{2})^{\frac{-1}{2}} \\ & \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}[-(1-x^{2})^{\frac{-1}{2}}] \\ & =-(-\frac{1}{2}) \cdot(1-x^{2})^{\frac{-3}{2}} \cdot \frac{d}{d x}(1-x^{2}) \\ & =\frac{1}{2 \sqrt{(1-x^{2})^{3}}} \times(-2 x) \\ & \Rightarrow \frac{d^{2} y}{d x^{2}}=\frac{-x}{\sqrt{(1-x^{2})^{3}}} \end{aligned} $
लाना $x=\cos y$ समीकरण (i) में, हम प्राप्त करते हैं
$\frac{d^{2} y}{d x^{2}}=\frac{-\cos y}{\sqrt{(1-\cos ^{2} y)^{3}}}$ $\Rightarrow \frac{d^{2} y}{d x^{2}}=\frac{-\cos y}{\sqrt{(\sin ^{2} y)^{3}}}$
$ =\frac{-\cos y}{\sin ^{3} y} $
$ =\frac{-\cos y}{\sin y} \times \frac{1}{\sin ^{2} y} $
$\Rightarrow \frac{d^{2} y}{d x^{2}}=-\cot y \cdot cosec^{2} y$
13. यदि $y=3 \cos (\log x)+4 \sin (\log x)$ है तो दर्शाइए कि $x^{2} y _{2}+x y _{1}+y=0$
Show Answer
समाधान
यह दिया गया है, $y=3 \cos (\log x)+4 \sin (\log x)$
तब,
$ \begin{aligned} & y_1=3 \cdot \frac{d}{d x}[\cos (\log x)]+4 \cdot \frac{d}{d x}[\sin (\log x)] \\ & =3 \cdot[-\sin (\log x) \cdot \frac{d}{d x}(\log x)]+4 \cdot[\cos (\log x) \cdot \frac{d}{d x}(\log x)] \\ & \therefore y_1=\frac{-3 \sin (\log x)}{x}+\frac{4 \cos (\log x)}{x}=\frac{4 \cos (\log x)-3 \sin (\log x)}{x} \\ & \therefore y_2=\frac{d}{d x}(\frac{4 \cos (\log x)-3 \sin (\log x)}{x}) \\ & =\frac{x{4 \cos (\log x)-3 \sin (\log x)}^{\prime}-{4 \cos (\log x)-3 \sin (\log x)}(x)^{\prime}}{x^{2}} \\ & =\frac{x[4{\cos (\log x)}^{\prime}-3{\sin (\log x)}^{\prime}]-{4 \cos (\log x)-3 \sin (\log x)} \cdot 1}{x^{2}} \\ & =\frac{x[-4 \sin (\log x) \cdot(\log x)^{\prime}-3 \cos (\log x) \cdot(\log x)^{\prime}]-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{x[-4 \sin (\log x) \cdot \frac{1}{x}-3 \cos (\log x) \cdot \frac{1}{x}]-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{-4 \sin (\log x)-3 \cos (\log x)-4 \cos (\log x)+3 \sin (\log x)}{x^{2}} \\ & =\frac{-\sin (\log x)-7 \cos (\log x)}{x^{2}} \\ & \therefore x^{2} y_2+x y_1+y \\ & =x^{2}(\frac{-\sin (\log x)-7 \cos (\log x)}{x^{2}})+x(\frac{4 \cos (\log x)-3 \sin (\log x)}{x})+3 \cos (\log x)+4 \sin (\log x) \\ & =-\sin (\log x)-7 \cos (\log x)+4 \cos (\log x)-3 \sin (\log x)+3 \cos (\log x)+4 \sin (\log x) \\ & =0 \end{aligned} $
अत: सिद्ध हुआ।
14. यदि $y=\mathrm{A} e^{m x}+\mathrm{B} e^{n x}$ है तो दर्शाइए कि $\frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y=0$
Show Answer
समाधान
यह दिया गया है, $y=A e^{m x}+B e^{n x}$
तब,
$ \begin{aligned} & \frac{d y}{d x}=A \cdot \frac{d}{d x}(e^{m x})+B \cdot \frac{d}{d x}(e^{n x})=A \cdot e^{m x} \cdot \frac{d}{d x}(m x)+B \cdot e^{n x} \cdot \frac{d}{d x}(n x)=A m e^{n x x}+B n e^{n x} \\ & \frac{d^{2} y}{d x^{2}}=\frac{d}{d x}(A m e^{m x}+B n e^{n x})=A m \cdot \frac{d}{d x}(e^{m x})+B n \cdot \frac{d}{d x}(e^{n x}) \\ & =A m \cdot e^{m x} \cdot \frac{d}{d x}(m x)+B n \cdot e^{n x} \cdot \frac{d}{d x}(n x)=A m^{2} e^{m x}+B n^{2} e^{n x} \\ & \therefore \frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y \\ & =A m^{2} e^{m x}+B n^{2} e^{n x}-(m+n) \cdot(A m e^{m x}+B n e^{n x})+m n(A e^{m x}+B e^{n x}) \\ & =A m^{2} e^{n x x}+B n^{2} e^{n x}-A m^{2} e^{n x x}-B m n e^{n x}-A m n e^{m x x}-B n^{2} e^{n x}+A m n e^{n x x}+B m n e^{n x} \\ & =0 \end{aligned} $
अत: सिद्ध हुआ।
15. यदि $y=500 e^{7 x}+600 e^{-7 x}$ है तो दर्शाइए कि $\frac{d^{2} y}{d x^{2}}=49 y$ है।
Show Answer
समाधान
यह दिया गया है, $y=500 e^{7 x}+600 e^{-7 x}$
तब,
$ \begin{aligned} \frac{d y}{d x} & =500 \cdot \frac{d}{d x}(e^{7 x})+600 \cdot \frac{d}{d x}(e^{-7 x}) \\ & =500 \cdot e^{7 x} \cdot \frac{d}{d x}(7 x)+600 \cdot e^{-7 x} \cdot \frac{d}{d x}(-7 x) \\ & =3500 e^{7 x}-4200 e^{-7 x} \\ \therefore \frac{d^{2} y}{d x^{2}} & =3500 \cdot \frac{d}{d x}(e^{7 x})-4200 \cdot \frac{d}{d x}(e^{-7 x}) \\ & =3500 \cdot e^{7 x} \cdot \frac{d}{d x}(7 x)-4200 \cdot e^{-7 x} \cdot \frac{d}{d x}(-7 x) \\ & =7 \times 3500 \cdot e^{7 x}+7 \times 4200 \cdot e^{-7 x} \\ & =49 \times 500 e^{7 x}+49 \times 600 e^{-7 x} \\ & =49(500 e^{7 x}+600 e^{-7 x}) \\ & =49 y \end{aligned} $
अत: सिद्ध हुआ।
16. यदि $e^{y}(x+1)=1$ है तो दर्शाइए कि $\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}$ है।
Show Answer
समाधान
दिया गया रिश्ता है $e^{y}(x+1)=1$
$e^{y}(x+1)=1$
$\Rightarrow e^{y}=\frac{1}{x+1}$
दोनों पक्षों पर लघुगणक लेने पर, हम प्राप्त करते हैं
$y=\log \frac{1}{(x+1)}$
$x$ के संबंध में इस संबंध को अलग करने पर, हम प्राप्त करते हैं $\frac{d y}{d x}=(x+1) \frac{d}{d x}(\frac{1}{x+1})=(x+1) \cdot \frac{-1}{(x+1)^{2}}=\frac{-1}{x+1}$
$\therefore \frac{d^{2} y}{d x^{2}}=-\frac{d}{d x}(\frac{1}{x+1})=-(\frac{-1}{(x+1)^{2}})=\frac{1}{(x+1)^{2}}$
$\Rightarrow \frac{d^{2} y}{d x^{2}}=(\frac{-1}{x+1})^{2}$
$\Rightarrow \frac{d^{2} y}{d x^{2}}=(\frac{d y}{d x})^{2}$
अत: सिद्ध हुआ।
17. यदि $y=\left(\tan ^{-1} x\right)^{2}$ है तो दर्शाइए कि $\left(x^{2}+1\right)^{2} y _{2}+2 x\left(x^{2}+1\right) y _{1}=2$ है।
Show Answer
समाधान
दिया गया रिश्ता है $y=(\tan ^{-1} x)^{2}$
तब,
$y_1=2 \tan ^{-1} x \frac{d}{d x}(\tan ^{-1} x)$
$\Rightarrow y_1=2 \tan ^{-1} x \cdot \frac{1}{1+x^{2}}$
$\Rightarrow(1+x^{2}) y_1=2 \tan ^{-1} x$
फिर से दोनों पक्षों पर $x$ के संबंध में अंतर करने पर, हम प्राप्त करते हैं
$(1+x^{2}) y_2+2 x y_1=2(\frac{1}{1+x^{2}})$
$\Rightarrow(1+x^{2})^{2} y_2+2 x(1+x^{2}) y_1=2$
अत: सिद्ध हुआ।
विविध उदाहरण
उदाहरण 38 $x$ के सापेक्ष निम्नलिखित का अवकलन कीजिए:
(i) $\sqrt{3 x+2}+\frac{1}{\sqrt{2 x^{2}+4}}$
(ii) $\log _{7}(\log x)$
हल
(i) मान लीजिए कि $y=\sqrt{3 x+2}+\frac{1}{\sqrt{2 x^{2}+4}}=(3 x+2)^{\frac{1}{2}}+\left(2 x^{2}+4\right)^{-\frac{1}{2}}$ है।
ध्यान दीजिए कि यह फलन सभी वास्तविक संख्याओं $x>-\frac{2}{3}$ के लिए परिभाषित है। इसलिए
$$ \begin{aligned} \frac{d y}{d x} & =\frac{1}{2}(3 x+2)^{\frac{1}{2}-1} \cdot \frac{d}{d x}(3 x+2)+\left(-\frac{1}{2}\right)\left(2 x^{2}+4\right)^{-\frac{1}{2}-1} \cdot \frac{d}{d x}\left(2 x^{2}+4\right) \\ & =\frac{1}{2}(3 x+2)^{-\frac{1}{2}} \cdot(3)-\left(\frac{1}{2}\right)\left(2 x^{2}+4\right)^{-\frac{3}{2}} \cdot 4 x \\ & =\frac{3}{2 \sqrt{3 x+2}}-\frac{2 x}{\left(2 x^{2}+4\right)^{\frac{3}{2}}} \end{aligned} $$
यह सभी वास्तविक संख्याओं $x>-\frac{2}{3}$ के लिए परिभाषित है। (ii) मान लीजिए कि $y=\log _{7}(\log x)=\frac{\log (\log x)}{\log 7}$ (आधार परिवर्तन के सूत्र द्वारा)
समस्त वास्तविक संख्याओं $x>1$ के लिए फलन परिभाषित है। इसलिए
$$ \begin{aligned} \frac{d y}{d x} & =\frac{1}{\log 7} \frac{d}{d x}(\log (\log x)) \\ & =\frac{1}{\log 7} \frac{1}{\log x} \cdot \frac{d}{d x}(\log x) \\ & =\frac{1}{x \log 7 \log x} \end{aligned} $$
उदाहरण 39 $x$ के सापेक्ष निम्नलिखित का अवकलन कीजिए:
(i) $\cos ^{-1}(\sin x)$
(ii) $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)$
(iii) $\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)$
हल
(i) मान लीजिए कि $f(x)=\cos ^{-1}(\sin x)$ है। ध्यान दीजिए कि यह फलन सभी वास्तविक संख्याओं के लिए परिभाषित है। हम इसे निम्नलिखित रूप में लिख सकते हैं।
$$ \begin{aligned} f(x) & =\cos ^{-1}(\sin x) \\ & =\cos ^{-1}\left[\cos \left(\frac{\pi}{2}-x\right)\right], \text { since } \frac{\pi}{2}-x \in[0 . \pi] \\ & =\frac{\pi}{2}-x \end{aligned} $$
अत: $$ f^{\prime}(x)=-1 \text { है। } $$
(ii) मान लीजिए कि $f(x)=\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)$ है। ध्यान दीजिए कि यह फलन उन सभी वास्तविक संख्याओं के लिए परिभाषित है जिनके लिए $\cos x \neq-1$, अर्थात् $\pi$ के समस्त विषम गुणजों के अतिरिक्त अन्य सभी वास्तविक संख्याओं के लिए हम इस फलन को निम्नलिखित प्रकार से पुनः व्यक्त कर सकते हैं:
$$ \begin{aligned} f(x) & =\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right) \\ & =\tan ^{-1}\left[\frac{2 \sin \left(\frac{x}{2}\right) \cos \left(\frac{x}{2}\right)}{2 \cos ^{2} \frac{x}{2}}\right] \\ & =\tan ^{-1}\left[\tan \left(\frac{x}{2}\right)\right]=\frac{x}{2} \end{aligned} $$
ध्यान दीजिए कि हम अंश तथा हर में $\cos \left(\frac{x}{2}\right)$ को काट सके, क्योंकि यह शून्य के बराबर नहीं है। अत: $f^{\prime}(x)=\frac{1}{2}$ है।
(iii) मान लीजिए कि $f(x)=\sin ^{-1}\left(\frac{2^{x+1}}{1+4^{x}}\right)$ है। इस फलन का प्रांत ज्ञात करने के लिए हमें उन सभी $x$ को ज्ञात करने की आवश्यकता है जिनके लिए $-1 \leq \frac{2^{x+1}}{1+4^{x}} \leq 1$ है। क्योंकि $\frac{2^{x+1}}{1+4^{x}}$ सदैव धन राशि है, इसलिए हमें उन सभी $x$ को ज्ञात करना है जिनके लिए $\frac{2^{x+1}}{1+4^{x}} \leq 1$, अर्थात् वे सभी $x$ जिनके लिए $2^{x+1} \leq 1+4^{x}$ है। हम इसको $2 \leq \frac{1}{2^{x}}+2^{x}$ प्रकार भी लिख सकते हैं, जो सभी $x$ के लिए सत्य है। अतः फलन प्रत्येक वास्तविक संख्या के लिए परिभाषित है। अब $2^{x}=\tan \theta$ रखने पर यह फलन निम्नलिखित प्रकार से पुन: लिखा जा सकता है:
$ \begin{aligned} f(x) & =\sin ^{-1}\left[\frac{2^{x+1}}{1+4^{x}}\right] \\ & =\sin ^{-1}\left[\frac{2^{x} \cdot 2}{1+\left(2^{x}\right)^{2}}\right] \\ & =\sin ^{-1}\left[\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right] \\ & =\sin ^{-1}[\sin 2 \theta]=2 \theta=2 \tan ^{-1}\left(2^{x}\right) \\ \end{aligned} $
अतः $$ \begin{aligned} f^{\prime}(x) & =2 \cdot \frac{1}{1+\left(2^{x}\right)^{2}} \cdot \frac{d}{d x}\left(2^{x}\right) \\ & =\frac{2}{1+4^{x}} \cdot\left(2^{x}\right) \log 2 \\ & =\frac{2^{x+1} \log 2}{1+4^{x}} \end{aligned} $$
उदाहरण 40 यदि सभी $0<x<\pi$ के लिए $f(x)=(\sin x)^{\sin x}$ है तो $f^{\prime}(x)$ ज्ञात कीजिए।
हल यहाँ फलन $y=(\sin x)^{\sin x}$ सभी धन वास्तविक संख्याओं के लिए परिभाषित है। लघुगणक लेने पर
अब $$ \begin{aligned} \log y & =\log (\sin x)^{\sin x}=\sin x \log (\sin x) \\ \frac{1}{y} \frac{d y}{d x} & =\frac{d}{d x}(\sin x \log (\sin x)) \\ & =\cos x \log (\sin x)+\sin x \cdot \frac{1}{\sin x} \cdot \frac{d}{d x}(\sin x) \\ & =\cos x \log (\sin x)+\cos x \\ & =(1+\log (\sin x)) \cos x \end{aligned} $$
अब $ \frac{d y}{d x}=y((1+\log (\sin x)) \cos x)=(1+\log (\sin x))(\sin x)^{\sin x} \cos x $
उदाहरण 41 धनात्मक अचर $a$ के लिए $\frac{d y}{d x}$, ज्ञात कीजिए, जहाँ
$$ y=a^{t+\frac{1}{t}} \text {, तथा } x=\left(t+\frac{1}{t}\right)^{a} \text { है। } $$
हल ध्यान दीजिए कि दोनों $y$ तथा $x$, समस्त वास्तविक संख्या $t \neq 0$ के लिए परिभाषित हैं। स्पष्टतः
$$ \begin{aligned} \frac{d y}{d t}=\frac{d}{d t}\left(a^{t+\frac{1}{t}}\right) & =a^{t+\frac{1}{t}} \frac{d}{d t}\left(t+\frac{1}{t}\right) \cdot \log a \\ & =a^{t+\frac{1}{t}}\left(1-\frac{1}{t^{2}}\right) \log a \\ \frac{d x}{d t} & =a\left[t+\frac{1}{t}\right]^{a-1} \cdot \frac{d}{d t}\left(t+\frac{1}{t}\right) \\ & =a\left[t+\frac{1}{t}\right]^{a-1} \cdot\left(1-\frac{1}{t^{2}}\right) \\ \frac{d x}{d t} & \neq 0 \text { केवल यदि } t \neq \pm 1 \text { है। अतः } t \neq \pm 1 \text { के लिए } \\ \frac{d y}{d x}=\frac{d y}{\frac{d x}{d t}} & =\frac{a^{t+\frac{1}{t}}\left(1-\frac{1}{t^{2}}\right) \log a}{\left.a^{\left[t+\frac{1}{t}\right.}\right]^{a-1} \cdot\left(1-\frac{1}{t^{2}}\right)}=\frac{a^{t+\frac{1}{t}} \log a}{a\left(t+\frac{1}{t}\right)^{a-1}} \end{aligned} $$
उदाहरण 42 $e^{\cos x}$ के सापेक्ष $\sin ^{2} x$ का अवकलन कीजिए।
हल मान लीजिए कि $u(x)=\sin ^{2} x$ तथा $v(x)=e^{\cos x}$ है। यहाँ हमें $\frac{d u}{d v}=\frac{d u / d x}{d v / d x}$ ज्ञात करना है। स्पष्टतः
$$ \begin{aligned} & \frac{d u}{d x}=2 \sin x \cos x \text { और } \frac{d v}{d x}=e^{\cos x}(-\sin x)=-(\sin x) e^{\cos x} \text { है। } \\ & \frac{d u}{d v}=\frac{2 \sin x \cos x}{-\sin x e^{\cos x}}=-\frac{2 \cos x}{e^{\cos x}} \end{aligned} $$
अध्याय 5 पर विविध प्रश्नावली
प्रश्न संख्या 1 से 11 तक प्रदत्त फलनों का, $x$ के सापेक्ष अवकलन कीजिए:
1. $\left(3 x^{2}-9 x+5\right)^{9}$
Show Answer
#missing2. $\sin ^{3} x+\cos ^{6} x$
Show Answer
#missing3. $(5 x)^{3 \cos x 2 x}$
Show Answer
#missing4. $\sin ^{-1}(x \sqrt{x}), 0 \leq x \leq 1$.
Show Answer
#missing5. $\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}},-2<x<2$.
Show Answer
#missing6. $\cot ^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right], 0<x<\frac{\pi}{2}$
Show Answer
#missing7. $(\log x)^{\log x}, x>1$
Show Answer
#missing8. $\cos (a \cos x+b \sin x)$, किन्हीं अचर $a$ तथा $b$ के लिए
Show Answer
#missing9. $(\sin x-\cos x)^{(\sin x-\cos x)}, \frac{\pi}{4}<x<\frac{3 \pi}{4}$
Show Answer
#missing10. $x^{x}+x^{a}+a^{x}+a^{a}$, किसी नियत $a>0$ तथा $x>0$ के लिए
Show Answer
#missing11. $x^{x^{2}-3}+(x-3)^{x^{2}}, x>3$ के लिए
Show Answer
#missing12. यदि $y=12(1-\cos t), x=10(t-\sin t),-\frac{\pi}{2}<t<\frac{\pi}{2}$ तो $\frac{d y}{d x}$ ज्ञात कीजिए।
Show Answer
#missing13. यदि $y=\sin ^{-1} x+\sin ^{-1} \sqrt{1-x^{2}}, 0<x<1$ है तो $\frac{d y}{d x}$ ज्ञात कीजिए।
Show Answer
#missing14. यदि $-1<x<1$ के लिए $x \sqrt{1+y}+y \sqrt{1+x}=0$ है तो सिद्ध कीजिए कि $\frac{d y}{d x}=-\frac{1}{(1+x)^{2}}$
Show Answer
#missing15. यदि किसी $c>0$ के लिए $(x-a)^{2}+(y-b)^{2}=c^{2}$ है तो सिद्ध कीजिए कि $\frac{\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}}{\frac{d^{2} y}{d x^{2}}}, a \text { और } b$ से स्वतंत्र एक स्थिर राशि है।
Show Answer
#missing16. यदि $\cos y=x \cos (a+y)$, तथा $\cos a \neq \pm 1$, तो सिद्ध कीजिए कि $\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}$
Show Answer
#missing17. यदि $x=a(\cos t+t \sin t)$ और $y=a(\sin t-t \cos t)$, तो $\frac{d^{2} y}{d x^{2}}$ ज्ञात कीजिए।
Show Answer
#missing18. यदि $f(x)=|x|^{3}$, तो प्रमाणित कीजिए कि $f^{\prime \prime}(x)$ का अस्तित्व है और इसे ज्ञात भी कीजिए।
Show Answer
#missing19. $\sin (\mathrm{A}+\mathrm{B})=\sin \mathrm{A} \cos \mathrm{B}+\cos \mathrm{A} \sin \mathrm{B}$ का प्रयोग करते हुए अवकलन द्वारा cosines के लिए योग सूत्र ज्ञात कीजिए।
Show Answer
#missing20. क्या एक ऐसे फलन का अस्तित्व है, जो प्रत्येक बिंदु पर संतत हो किंतु केवल दो बिंदुओं पर अवकलनीय न हो? अपने उत्तर का औचित्य भी बतलाइए।
Show Answer
#missing21. यदि $y=\left|\begin{array}{ccc}f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c\end{array}\right|$ है तो सिद्ध कीजिए कि $\frac{d y}{d x}=\left|\begin{array}{ccc}f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c\end{array}\right|$
Show Answer
#missing22. यदि $y=e^{a \cos ^{-1} x},-1 \leq x \leq 1$, तो दर्शाइए कि $$ \left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y=0 $$
Show Answer
#missingसारांश
-
एक वास्तविक मानीय फलन अपने प्रांत के किसी बिंदु पर संतत होता है यदि उस बिंदु पर फलन की सीमा, उस बिंदु पर फलन के मान के बराबर होती है।
-
संतत फलनों के योग, अंतर, गुणनफल और भागफल संतत होते हैं, अर्थात्, यदि $f$ तथा $g$ संतत फलन हैं, तो
$(f \pm g)(x)=f(x) \pm g(x)$ संतत होता है।
$(f . g)(x)=f(x) . g(x)$ संतत होता है।
$\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$ (जहाँ $g(x) \neq 0$ ) संतत होता है।
- प्रत्येक अवकलनीय फलन संतत होता है किंतु इसका विलोम सत्य नहीं है।
- श्रृंखला-नियम फलनों के संयोजन का अवकलन करने के लिए एक नियम है। यदि $f=v 0 u, t=u(x)$ और यदि $\frac{d t}{d x}$ तथा $\frac{d v}{d t}$ का अस्तित्व है तो
$$ \frac{d f}{d x}=\frac{d v}{d t} \cdot \frac{d t}{d x} $$
- कुछ मानक अवकलज (परिभाषित प्रांतों में) निम्नलिखित हैं:
$$ \begin{array}{ll} \frac{d}{d x}\left(\sin ^{-1} x\right)=\frac{1}{\sqrt{1-x^{2}}} & \frac{d}{d x}\left(\cos ^{-1} x\right)=\frac{-1}{\sqrt{1-x^{2}}} \\ \frac{d}{d x}\left(\tan ^{-1} x\right)=\frac{1}{1+x^{2}} & \frac{d}{d x}(\log x)=\frac{1}{x} \end{array} $$
- लघुगणकीय अवकलन, $f(x)=[u(x)]^{v(x)}$ के रूप के फलनों के अवकलन करने के लिए एक सशक्त तकनीक है। इस तकनीक के अर्थपूर्ण होने के लिए आवश्यक है कि $f(x)$ तथा $u(x)$ दोनों ही धनात्मक हों।










