Chapter-04 Chemical Bonding and Molecular Structure
“Scientists are constantly discovering new compounds, orderly arranging the facts about them, trying to explain with the existing knowledge, organising to modify the earlier views or evolve theories for explaining the newly observed facts.”
Matter is made up of one or different type of elements. Under normal conditions no other element exists as an independent atom in nature, except noble gases. However, a group of atoms is found to exist together as one species having characteristic properties. Such a group of atoms is called a molecule. Obviously there must be some force which holds these constituent atoms together in the molecules. The attractive force which holds various constituents (atoms, ions, etc.) together in different chemical species is called a chemical bond. Since the formation of chemical compounds takes place as a result of combination of atoms of various elements in different ways, it raises many questions. Why do atoms combine? Why are only certain combinations possible? Why do some atoms combine while certain others do not? Why do molecules possess definite shapes? To answer such questions different theories and concepts have been put forward from time to time. These are Kössel-Lewis approach, Valence Shell Electron Pair Repulsion (VSEPR) Theory, Valence Bond (VB) Theory and Molecular Orbital (MO) Theory. The evolution of various theories of valence and the interpretation of the nature of chemical bonds have closely been related to the developments in the understanding of the structure of atom, the electronic configuration of elements and the periodic table. Every system tends to be more stable and bonding is nature’s way of lowering the energy of the system to attain stability.
4.1 KÖSSEL-LEWIS APPROACH TO CHEMICAL BONDING
In order to explain the formation of chemical bond in terms of electrons, a number of attempts were made, but it was only in 1916 when Kössel and Lewis succeeded independently in giving a satisfactory explanation. They were the first to provide some logical explanation of valence which was based on the inertness of noble gases.
Lewis pictured the atom in terms of a positively charged ‘Kernel’ (the nucleus plus the inner electrons) and the outer shell that could accommodate a maximum of eight electrons. He, further assumed that these eight electrons occupy the corners of a cube which surround the ‘Kernel’. Thus the single outer shell electron of sodium would occupy one corner of the cube, while in the case of a noble gas all the eight corners would be occupied. This octet of electrons, represents a particularly stable electronic arrangement. Lewis postulated that atoms achieve the stable octet when they are linked by chemical bonds. In the case of sodium and chlorine, this can happen by the transfer of an electron from sodium to chlorine thereby giving the $\mathrm{Na}^+$ and $\mathrm{Cl}^{-}$ ions. In the case of other molecules like $ \mathrm{Cl}_2, \mathrm{H}_2, \mathrm{~F}_2 $ , etc., the bond is formed by the sharing of a pair of electrons between the atoms. In the process each atom attains a stable outer octet of electrons.
Lewis Symbols: In the formation of a molecule, only the outer shell electrons take part in chemical combination and they are known as valence electrons. The inner shell electrons are well protected and are generally not involved in the combination process. G.N. Lewis, an American chemist introduced simple notations to represent valence electrons in an atom. These notations are called Lewis symbols. For example, the Lewis symbols for the elements of second period are as under:

Significance of Lewis Symbols : The number of dots around the symbol represents the number of valence electrons. This number of valence electrons helps to calculate the common or group valence of the element. The group valence of the elements is generally either equal to the number of dots in Lewis symbols or 8 minus the number of dots or valence electrons.
Kössel, in relation to chemical bonding, drew attention to the following facts:
- In the periodic table, the highly electronegative halogens and the highly electropositive alkali metals are separated by the noble gases;
- The formation of a negative ion from a halogen atom and a positive ion from an alkali metal atom is associated with the gain and loss of an electron by the respective atoms;
- The negative and positive ions thus formed attain stable noble gas electronic configurations. The noble gases (with the exception of helium which has a duplet of electrons) have a particularly stable outer shell configuration of eight (octet) electrons, $n s^{2} n p^{6}$.
- The negative and positive ions are stabilized by electrostatic attraction.
For example, the formation of $\mathrm{NaCl}$ from sodium and chlorine, according to the above scheme, can be explained as:
| $\mathrm{Na}$ | $\rightarrow$ | $\mathrm{Na}^{+}+\mathrm{e}^{-}$ |
| $[\mathrm{Ne}] 3 \mathrm{~s}^{1}$ | $[\mathrm{Ne}]$ | |
| $\mathrm{Cl}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{Cl}^{-}$ |
| $[\mathrm{Ne}] 3 s^{2} 3 p^{5}$ | $[\mathrm{Ne}] 3 s^{2} 3 p^{6}$ or $[\mathrm{Ar}]$ | |
| $\mathrm{Na}^{+}+\mathrm{Cl}^{-}$ | $\rightarrow$ | $\mathrm{NaCl}$ or $\mathrm{Na}^{+} \mathrm{Cl}^{-}$ |
Similarly the formation of $\mathrm{CaF}_{2}$ may be shown as:
| $\mathrm{Ca}$ | $\rightarrow$ | $\mathrm{Ca}^{2+}+2 \mathrm{e}^{-}$ |
| $[\mathrm{Ar}] 4 s^{2}$ | $[\mathrm{Ar}]$ | |
| $\mathrm{F}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{F}^{-}$ |
| $[\mathrm{He}] 2 s^{2} 2 p^{5}$ | $[\mathrm{He}] 2 s^{2} 2 p^{6}$ or $[\mathrm{Ne}]$ | |
| $\mathrm{Ca}^{2+}+2 \mathrm{~F}^{-}$ | $\rightarrow$ | $\mathrm{CaF}_2$ or $\mathrm{Ca}^{2+}\left(\mathrm{F}^{-}\right)_2$ |
The bond formed, as a result of the electrostatic attraction between the positive and negative ions was termed as the electrovalent bond. The electrovalence is thus equal to the number of unit charge(s) on the ion. Thus, calcium is assigned a positive electrovalence of two, while chlorine a negative electrovalence of one.
Kössel’s postulations provide the basis for the modern concepts regarding ion-formation by electron transfer and the formation of ionic crystalline compounds. His views have proved to be of great value in the understanding and systematisation of the ionic compounds. At the same time he did recognise the fact that a large number of compounds did not fit into these concepts.
4.1.1 Octet Rule
Kössel and Lewis in 1916 developed an important theory of chemical combination between atoms known as electronic theory of chemical bonding. According to this, atoms can combine either by transfer of valence electrons from one atom to another (gaining or losing) or by sharing of valence electrons in order to have an octet in their valence shells. This is known as octet rule.
4.1.2 Covalent Bond
Langmuir (1919) refined the Lewis postulations by abandoning the idea of the stationary cubical arrangement of the octet, and by introducing the term covalent bond. The Lewis-Langmuir theory can be understood by considering the formation of the chlorine molecule, $\mathrm{Cl}_2$. The $\mathrm{Cl}$ atom with electronic configuration, $[\mathrm{Ne}] 3 s^2 3 p^5$, is one electron short of the argon configuration. The formation of the $\mathrm{Cl}_2$ molecule can be understood in terms of the sharing of a pair of electrons between the two chlorine atoms, each chlorine atom contributing one electron to the shared pair. In the process both chlorine atoms attain the outer shell octet of the nearest noble gas (i.e., argon).

Covalent bond between two Cl atoms
The dots represent electrons. Such structures are referred to as Lewis dot structures.
The Lewis dot structures can be written for other molecules also, in which the combining atoms may be identical or different. The important conditions being that:
- Each bond is formed as a result of sharing of an electron pair between the atoms.
- Each combining atom contributes at least one electron to the shared pair.
- The combining atoms attain the outershell noble gas configurations as a result of the sharing of electrons.
- Thus in water and carbon tetrachloride molecules, formation of covalent bonds can be represented as:

Thus, when two atoms share one electron pair they are said to be joined by a single covalent bond. In many compounds we have multiple bonds between atoms. The formation of multiple bonds envisages sharing of more than one electron pair between two atoms. If two atoms share two pairs of electrons, the covalent bond between them is called a double bond. For example, in the carbon dioxide molecule, we have two double bonds between the carbon and oxygen atoms. Similarly in ethene molecule the two carbon atoms are joined by a double bond..

$\mathrm{C} _{2} \mathrm{H} _{4}$ Molecule
When combining atoms share three electron pairs as in the case of two nitrogen atoms in the $N_{2}$ molecule and the two carbon atoms in the ethyne molecule, a triple bond is formed.
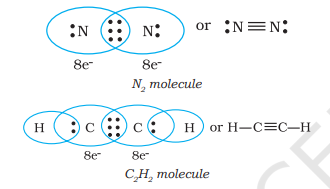
4.1.3 Lewis Representation of Simple Molecules (the Lewis Structures)
The Lewis dot structures provide a picture of bonding in molecules and ions in terms of the shared pairs of electrons and the octet rule. While such a picture may not explain the bonding and behaviour of a molecule completely, it does help in understanding the formation and properties of a molecule to a large extent. Writing of Lewis dot structures of molecules is, therefore, very useful. The Lewis dot structures can be written by adopting the following steps:
- The total number of electrons required for writing the structures are obtained by adding the valence electrons of the combining atoms. For example, in the $\mathrm{CH}_{4}$ molecule there are eight valence electrons available for bonding ( 4 from carbon and 4 from the four hydrogen atoms).
- For anions, each negative charge would mean addition of one electron. For cations, each positive charge would result in subtraction of one electron from the total number of valence electrons. For example, for the $CO_3^{2-}$ ion, the two negative charges indicate that there are two additional electrons than those provided by the neutral atoms. For $\mathrm{NH}_{4}^{+}$ ion, one positive charge indicates the loss of one electron from the group of neutral atoms.
- Knowing the chemical symbols of the combining atoms and having knowledge of the skeletal structure of the compound (known or guessed intelligently), it is easy to distribute the total number of electrons as bonding shared pairs between the atoms in proportion to the total bonds.
- In general the least electronegative atom occupies the central position in the molecule/ion. For example in the $\mathrm{NF}_3$ and $CO_3^{2-}$, nitrogen and carbon are the central atoms whereas fluorine and oxygen occupy the terminal positions.
- After accounting for the shared pairs of electrons for single bonds, the remaining electron pairs are either utilized for multiple bonding or remain as the lone pairs. The basic requirement being that each bonded atom gets an octet of electrons.
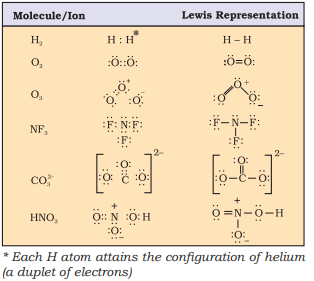
Lewis representations of a few molecules/ ions are given in Table 4.1.
Table 4.1 The Lewis Representation of Some Molecules
Problem 4.1
Write the Lewis dot structure of $\mathrm{CO}$ molecule.
Solution
Step 1. Count the total number of valence electrons of carbon and oxygen atoms. The outer (valence) shell configurations of carbon and oxygen atoms are: $2 s^{2} 2 p^{2}$ and $2 s^{2} 2 p^{4}$, respectively. The valence electrons available are $4+6=10$.
Step 2. The skeletal structure of $\mathrm{CO}$ is written as: C O
Step 3. Draw a single bond (one shared electron pair) between $\mathrm{C}$ and $\mathrm{O}$ and complete the octet on $\mathrm{O}$, the remaining two electrons are the lone pair on $\mathrm{C}$.
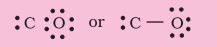
This does not complete the octet on carbon and hence we have to resort to multiple bonding (in this case a triple bond) between $\mathrm{C}$ and $\mathrm{O}$ atoms. This satisfies the octet rule condition for both atoms.
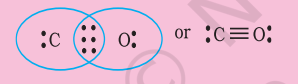
Problem 4.2
Write the Lewis structure of the nitrite ion, $\mathrm{NO}_{2}^{-}$.
Solution
Step 1. Count the total number of valence electrons of the nitrogen atom, the oxygen atoms and the additional one negative charge (equal to one electron).
$$ \begin{aligned} & \mathrm{N}\left(2 s^{2} 2 p^{3}\right), \mathrm{O}\left(2 s^{2} 2 p^{4}\right) \\ & 5+(2 \times 6)+ = 17 \text { electrons } \end{aligned} $$
Total number of electrons when one electron is deposited for unit negative charge = 17+1 = 18
Step 2. The skeletal structure of $\mathrm{NO}_{2}^{-}$is written as: $\mathrm{O} \quad \mathrm{N} \mathrm{O}$
Step 3. Draw a single bond (one shared electron pair) between the nitrogen and each of the oxygen atoms completing the octets on oxygen atoms. This, however, does not complete the octet on nitrogen if the remaining two electrons constitute lone pair on it.

Hence we have to resort to multiple bonding between nitrogen and one of the oxygen atoms (in this case a double bond). This leads to the following Lewis dot structures.
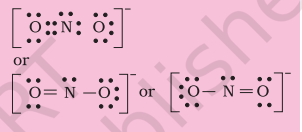
4.1.4 Formal Charge
Lewis dot structures, in general, do not represent the actual shapes of the molecules. In case of polyatomic ions, the net charge is possessed by the ion as a whole and not by a particular atom. It is, however, feasible to assign a formal charge on each atom. The formal charge of an atom in a polyatomic molecule or ion may be defined as the difference between the number of valence electrons of that atom in an isolated or free state and the number of electrons assigned to that atom in the Lewis structure. It is expressed as :

The counting is based on the assumption that the atom in the molecule owns one electron of each shared pair and both the electrons of a lone pair.
Let us consider the ozone molecule $\left(\mathrm{O}_3\right)$. The Lewis structure of $\mathrm{O}_3$ may be drawn as:
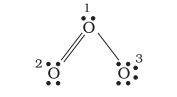
The atoms have been numbered as 1,2 and 3. The formal charge on:
- The central $\mathrm{O}$ atom marked 1 $=6-2-\frac{1}{2}(6)=+1$
- The end $\mathrm{O}$ atom marked 2 $=6-4-\frac{1}{2}(4)=0$
- The end $\mathrm{O}$ atom marked 3 $=6-6-\frac{1}{2}(2)=-1$
Hence, we represent $\mathrm{O}_{3}$ along with the formal charges as follows:
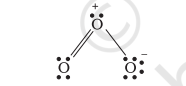
We must understand that formal charges do not indicate real charge separation within the molecule. Indicating the charges on the atoms in the Lewis structure only helps in keeping track of the valence electrons in the molecule. Formal charges help in the selection of the lowest energy structure from a number of possible Lewis structures for a given species. Generally the lowest energy structure is the one with the smallest formal charges on the atoms. The formal charge is a factor based on a pure covalent view of bonding in which electron pairs are shared equally by neighbouring atoms.
4.1.5 Limitations of the Octet Rule
The octet rule, though useful, is not universal. It is quite useful for understanding the structures of most of the organic compounds and it applies mainly to the second period elements of the periodic table. There are three types of exceptions to the octet rule.
The incomplete octet of the central atom
In some compounds, the number of electrons surrounding the central atom is less than eight. This is especially the case with elements having less than four valence electrons. Examples are $\mathrm{LiCl}, \mathrm{BeH}_2$ and $\mathrm{BCl}_3$.
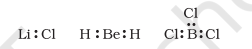
$\mathrm{Li}$, Be and B have 1, 2 and 3 valence electrons only. Some other such compounds are $\mathrm{AlCl}_3$ and $\mathrm{BF}_3$.
Odd-electron molecules
In molecules with an odd number of electrons like nitric oxide, $\mathrm{NO}$ and nitrogen dioxide, $\mathrm{NO}_2$, the octet rule is not satisfied for all the atoms
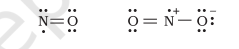
The expanded octet
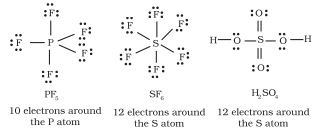
Elements in and beyond the third period of the periodic table have, apart from $3 s$ and $3 p$ orbitals, $3 d$ orbitals also available for bonding. In a number of compounds of these elements there are more than eight valence electrons around the central atom. This is termed as the expanded octet. Obviously the octet rule does not apply in such cases.
Some of the examples of such compounds are: $\mathrm{PF}_5, \mathrm{SF}_6, \mathrm{H}_2 \mathrm{SO}_4$ and a number of coordination compounds.
Interestingly, sulphur also forms many compounds in which the octet rule is obeyed. In sulphur dichloride, the $\mathrm{S}$ atom has an octet of electrons around it.
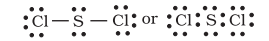
Other drawbacks of the octet theory
- It is clear that octet rule is based upon the chemical inertness of noble gases. However, some noble gases (for example xenon and krypton) also combine with oxygen and fluorine to form a number of compounds like $\mathrm{XeF}_2, \mathrm{KrF}_2, \mathrm{XeOF}_2$ etc.
- This theory does not account for the shape of molecules.
- It does not explain the relative stability of the molecules being totally silent about the energy of a molecule.
4.2 IONIC OR ELECTROVALENT BOND
From the Kössel and Lewis treatment of the formation of an ionic bond, it follows that the formation of ionic compounds would primarily depend upon:
- The ease of formation of the positive and negative ions from the respective neutral atoms;
- The arrangement of the positive and negative ions in the solid, that is, the lattice of the crystalline compound.
The formation of a positive ion involves ionization, i.e., removal of electron(s) from the neutral atom and that of the negative ion involves the addition of electron(s) to the neutral atom.
| $\mathrm{M}(\mathrm{g}) $ | $\rightarrow$ | $\mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} ;$ | |
| Ionization enthalpy | |||
| $\mathrm{X}(\mathrm{g})+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{X}^{-}(\mathrm{g}) ;$ | |
| Electron gain enthalpy | |||
| $\mathrm{M}^{+}(\mathrm{g})+\mathrm{X}^{-}(\mathrm{g}) \rightarrow$ | $\mathrm{MX}(\mathrm{s})$ |
The electron gain enthalpy, $\Delta_{e g} \boldsymbol{H}$, is the enthalpy change (Unit 3), when a gas phase atom in its ground state gains an electron. The electron gain process may be exothermic or endothermic. The ionization, on the other hand, is always endothermic. Electron affinity, is the negative of the energy change accompanying electron gain.
Obviously ionic bonds will be formed more easily between elements with comparatively low ionization enthalpies and elements with comparatively high negative value of electron gain enthalpy.
Most ionic compounds have cations derived from metallic elements and anions from non-metallic elements. The ammonium ion, $\mathrm{NH}_{4}^{+}$(made up of two non-metallic elements) is an exception. It forms the cation of a number of ionic compounds.
Ionic compounds in the crystalline state consist of orderly three-dimensional arrangements of cations and anions held together by coulombic interaction energies. These compounds crystallise in different crystal structures determined by the size of the ions, their packing arrangements and other factors. The crystal structure of sodium chloride, $\mathrm{NaCl}$ (rock salt), for example is shown below.
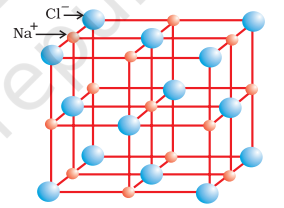
Rock salt structure
In ionic solids, the sum of the electron gain enthalpy and the ionization enthalpy may be positive but still the crystal structure gets stabilized due to the energy released in the formation of the crystal lattice. For example: the ionization enthalpy for $\mathrm{Na}^{+}(\mathrm{g})$ formation from $\mathrm{Na}(\mathrm{g})$ is $495.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$; while the electron gain enthalpy for the change $\mathrm{Cl}(\mathrm{g})+\mathrm{e}^{-} \rightarrow$ $\mathrm{Cl}^{-}(\mathrm{g})$ is, $-348.7 \mathrm{~kJ} \mathrm{~mol}^{-1}$ only. The sum of the two, $147.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$ is more than compensated for by the enthalpy of lattice formation of $\mathrm{NaCl}(\mathrm{s})\left(-788 \mathrm{~kJ} \mathrm{~mol}^{-1}\right)$. Therefore, the energy released in the processes is more than the energy absorbed. Thus a qualitative measure of the stability of an ionic compound is provided by its enthalpy of lattice formation and not simply by achieving octet of electrons around the ionic species in gaseous state.
Since lattice enthalpy plays a key role in the formation of ionic compounds, it is important that we learn more about it.
4.2.1 Lattice Enthalpy
The Lattice Enthalpy of an ionic solid is defined as the energy required to completely separate one mole of a solid ionic compound into gaseous constituent ions. For example, the lattice enthalpy of $\mathrm{NaCl}$ is $788 \mathrm{~kJ} \mathrm{~mol}^{-1}$. This means that 788 $\mathrm{kJ}$ of energy is required to separate one mole of solid $\mathrm{NaCl}$ into one mole of $\mathrm{Na}^{+}(\mathrm{g})$ and one mole of $\mathrm{Cl}^{-}(\mathrm{g})$ to an infinite distance.
This process involves both the attractive forces between ions of opposite charges and the repulsive forces between ions of like charge. The solid crystal being threedimensional; it is not possible to calculate lattice enthalpy directly from the interaction of forces of attraction and repulsion only. Factors associated with the crystal geometry have to be included.
4.3 BOND PARAMETERS
4.3.1 Bond Length
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule. Bond lengths are measured by spectroscopic, X-ray diffraction and electron-diffraction techniques about which you will learn in higher classes. Each atom of the bonded pair contributes to the bond length (Fig. 4.1). In the case of a covalent bond, the contribution from each atom is called the covalent radius of that atom.
The covalent radius is measured approximately as the radius of an atom’s core which is in contact with the core of an adjacent atom in a bonded situation. The covalent radius is half of the distance between two similar atoms joined by a covalent bond in the same molecule.
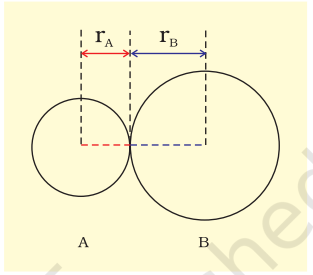
Fig. 4.1 The bond length in a covalent molecule AB. R = rA + rB (R is the bond length and rA and rB are the covalent radii of atoms A and B respectively)
The van der Waals radius represents the overall size of the atom which includes its valence shell in a nonbonded situation. Further, the van der Waals radius is half of the distance between two similar atoms in separate molecules in a solid. Covalent and van der Waals radii of chlorine are depicted in Fig. 4.2.
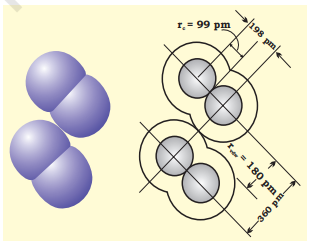
Fig. 4.2 Covalent and van der Waals radii in a chlorine molecule. The inner circles correspond to the size of the chlorine atom (rvdw and rc are van der Waals and covalent radii respectively).
Some typical average bond lengths for single, double and triple bonds are shown in Table 4.2. Bond lengths for some common molecules are given in Table 4.3.
The covalent radii of some common elements are listed in Table 4.4.
4.3.2 Bond Angle
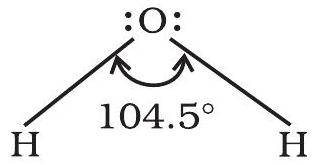
It is defined as the angle between the orbitals containing bonding electron pairs around the central atom in a molecule/complex ion. Bond angle is expressed in degree which can be experimentally determined by spectroscopic methods. It gives some idea regarding the distribution of orbitals around the central atom in a molecule/complex ion and hence it helps us in determining its shape. For example $\mathrm{H}-\mathrm{O}-\mathrm{H}$ bond angle in water can be represented as under :
4.3.3 Bond Enthalpy
It is defined as the amount of energy required to break one mole of bonds of a particular type between two atoms in a gaseous state. The unit of bond enthalpy is $\mathrm{kJ} \mathrm{mol}^{-1}$. For example, the $\mathrm{H}-\mathrm{H}$ bond enthalpy in hydrogen molecule is $435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$.
$\mathrm{H}_2 (\mathrm{~g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$;
$\Delta_{\mathrm{a}} H^\ominus =435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$
Similarly the bond enthalpy for molecules containing multiple bonds, for example $\mathrm{O}_2$ and $\mathrm{N}_2$ will be as under :
$\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})(\mathrm{g}) \rightarrow \mathrm{O}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} H^{\ominus}=498 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
$\mathrm{N}_{2}(\mathrm{~N} \equiv \mathrm{N})(\mathrm{g}) \rightarrow \mathrm{N}(\mathrm{g})+\mathrm{N}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} H^{\ominus}=946.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
It is important that larger the bond dissociation enthalpy, stronger will be the bond in the molecule. For a heteronuclear diatomic molecules like $\mathrm{HCl}$, we have
$$ \mathrm{HCl}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{Cl}(\mathrm{g}) ; \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=431.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
In case of polyatomic molecules, the measurement of bond strength is more complicated. For example in case of $\mathrm{H}_{2} \mathrm{O}$ molecule, the enthalpy needed to break the two $\mathrm{O}-\mathrm{H}$ bonds is not the same.
Table 4.2 Average Bond Lengths for Some Single, Double and Triple Bonds
| Bond Type | Covalent Bond Length (pm) |
|---|---|
| $\mathrm{O}-\mathrm{H}$ | 96 |
| $\mathrm{C}-\mathrm{H}$ | 107 |
| $\mathrm{~N}-\mathrm{O}$ | 136 |
| $\mathrm{C}-\mathrm{O}$ | 143 |
| $\mathrm{C}-\mathrm{N}$ | 143 |
| $\mathrm{C}-\mathrm{C}$ | 154 |
| $\mathrm{C}=\mathrm{O}$ | 121 |
| $\mathrm{~N}=\mathrm{O}$ | 122 |
| $\mathrm{C}=\mathrm{C}$ | 133 |
| $\mathrm{C}=\mathrm{N}$ | 138 |
| $\mathrm{C} \equiv \mathrm{N}$ | 116 |
| $\mathrm{C} \equiv \mathrm{C}$ | 120 |
Table 4.3 Bond Lengths in Some Common Molecules
| Molecule | Bond Length (pm) |
|---|---|
| $\mathrm{H}_{2}(\mathrm{H}-\mathrm{H})$ | 74 |
| $\mathrm{~F}_{2}(\mathrm{~F}-\mathrm{F})$ | 144 |
| $\mathrm{Cl}_{2}(\mathrm{Cl}-\mathrm{Cl})$ | 199 |
| $\mathrm{Br}_{2}(\mathrm{Br}-\mathrm{Br})$ | 228 |
| $\mathrm{I}_{2}(\mathrm{I}-\mathrm{I})$ | 267 |
| $\mathrm{~N}_{2}(\mathrm{~N} \equiv \mathrm{N})$ | 109 |
| $\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})$ | 121 |
| $\mathrm{HF}(\mathrm{H}-\mathrm{F})$ | 92 |
| $\mathrm{HCl}(\mathrm{H}-\mathrm{Cl})$ | 127 |
| $\mathrm{HBr}(\mathrm{H}-\mathrm{Br})$ | 141 |
| $\mathrm{HI}(\mathrm{H}-\mathrm{I})$ | 160 |
Table 4.4 Covalent Radii, $ \mathbf{r}_{\text {cov }} /(\mathrm{pm})$
| $\mathrm{H}$ | 37 | ||||||
|---|---|---|---|---|---|---|---|
| $\mathrm{C}$ | $77(1)$ | $\mathrm{N}$ | $74(1)$ | $\mathrm{O}$ | $66(1)$ | $\mathrm{F}$ | 64 |
| $67(2)$ | $65(2)$ | $57(2)$ | $\mathrm{Cl}$ | 99 | |||
| $60(3)$ | $55(3)$ | ||||||
| $\mathrm{P}$ | 110 | $\mathrm{~S}$ | $104(1)$ | $\mathrm{Br}$ | 114 | ||
| $95(2)$ | |||||||
| $\mathrm{As}$ | 121 | $\mathrm{Se}$ | 104 | $\mathrm{I}$ | 133 | ||
| $\mathrm{Sb}$ | 141 | $\mathrm{Te}$ | 137 |
- The values cited are for single bonds, except where otherwise indicated in parenthesis. (See also Unit 3 for periodic trends).
$\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) ; \Delta_a H_1^\ominus=502 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$\mathrm{OH}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ; \Delta_{\mathrm{a}} H_{2}^{\ominus}=427 \mathrm{~kJ} \mathrm{~mol}^{-1}$
The difference in the $\Delta_{\mathrm{a}} H^{\ominus}$ value shows that the second $\mathrm{O}-\mathrm{H}$ bond undergoes some change because of changed chemical environment. This is the reason for some difference in energy of the same $\mathrm{O}-\mathrm{H}$ bond in different molecules like $\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}$ (ethanol) and water. Therefore in polyatomic molecules the term mean or average bond enthalpy is used. It is obtained by dividing total bond dissociation enthalpy by the number of bonds broken as explained below in case of water molecule,
$ \text { Average bond enthalpy } =\frac{502+427}{2} $
$$ =464.5 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
4.3.4 Bond Order
In the Lewis description of covalent bond, the Bond Order is given by the number of bonds between the two atoms in a molecule. The bond order, for example in $\mathrm{H}_2$ (with a single shared electron pair), in $\mathrm{O}_2$ (with two shared electron pairs) and in $\mathrm{N}_2$ (with three shared electron pairs) is $1,2,3$ respectively. Similarly in CO (three shared electron pairs between $\mathrm{C}$ and $\mathrm{O}$) the bond order is 3 . For $\mathrm{N}_2$, bond order is 3 and its $\Delta_a H^\ominus$ is $946 \mathrm{~kJ} \mathrm{~mol}^{-1}$; being one of the highest for a diatomic molecule.
Isoelectronic molecules and ions have identical bond orders; for example, $F_2$ and $\mathrm{O}_{2}^{2-}$ have bond order 1. $\mathrm{N}_2, \mathrm{CO}$ and $\mathrm{NO}^{+}$ have bond order 3.
A general correlation useful for understanding the stablities of molecules is that: with increase in bond order, bond enthalpy increases and bond length decreases.
4.3.5 Resonance Structures
It is often observed that a single Lewis structure is inadequate for the representation of a molecule in conformity with its experimentally determined parameters. For example, the ozone, $\mathrm{O}_{3}$ molecule can be equally represented by the structures I and II shown below:
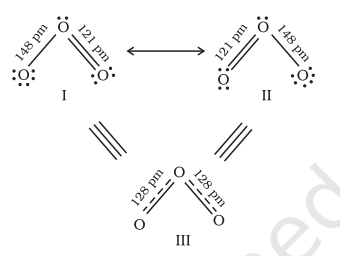
Fig. 4.3 Resonance in the O3 molecule
(structures I and II represent the two canonical forms while the structure III is the resonance hybrid)
In both structures we have a $\mathrm{O}-\mathrm{O}$ single bond and a $\mathrm{O}=\mathrm{O}$ double bond. The normal $\mathrm{O}-\mathrm{O}$ and $\mathrm{O}=\mathrm{O}$ bond lengths are $148 \mathrm{pm}$ and $121 \mathrm{pm}$ respectively. Experimentally determined oxygen-oxygen bond lengths in the $\mathrm{O}_3$ molecule are same ( $\left.128 \mathrm{pm}\right)$. Thus the oxygen-oxygen bonds in the $\mathrm{O}_3$ molecule are intermediate between a double and a single bond. Obviously, this cannot be represented by either of the two Lewis structures shown above.
The concept of resonance was introduced to deal with the type of difficulty experienced in the depiction of accurate structures of molecules like $\mathrm{O}_3$. According to the concept of resonance, whenever a single Lewis structure cannot describe a molecule accurately, a number of structures with similar energy, positions of nuclei, bonding and non-bonding pairs of electrons are taken as the canonical structures of the hybrid which describes the molecule accurately. Thus for $\mathrm{O}_3$, the two structures shown above constitute the canonical structures or resonance structures and their hybrid i.e., the III structure represents the structure of $\mathrm{O}_3$ more accurately. This is also called resonance hybrid. Resonance is represented by a double headed arrow.
Some of the other examples of resonance structures are provided by the carbonate ion and the carbon dioxide molecule.
Problem 4.3
Explain the structure of $\mathrm{CO}_{3}^{2-}$ ion in terms of resonance.
Solution
The single Lewis structure based on the presence of two single bonds and one double bond between carbon and oxygen atoms is inadequate to represent the molecule accurately as it represents unequal bonds. According to the experimental findings, all carbon to oxygen bonds in $\mathrm{CO}_{3}^{2-}$ are equivalent. Therefore the carbonate ion is best described as a resonance hybrid of the canonical forms I, II, and III shown below.
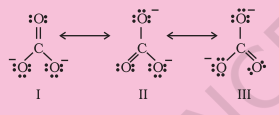
Fig. 4.4 Resonance in $\mathrm{CO}_{3}^{2-}, \mathrm{I}$, II and III represent the three canonical forms.
Problem 4.4
Explain the structure of $\mathrm{CO}_{2}$ molecule.
Solution
The experimentally determined carbon to oxygen bond length in $\mathrm{CO}_2$ is $115 \mathrm{pm}$. The lengths of a normal carbon to oxygen double bond $(\mathrm{C}=\mathrm{O})$ and carbon to oxygen triple bond $(\mathrm{C} \equiv \mathrm{O})$ are $121 \mathrm{pm}$ and $110 \mathrm{pm}$ respectively. The carbon-oxygen bond lengths in $\mathrm{CO}_2(115 \mathrm{pm})$ lie between the values for $\mathrm{C}=\mathrm{O}$ and $\mathrm{C} \equiv \mathrm{O}$. Obviously, a single Lewis structure cannot depict this position and it becomes necessary to write more than one Lewis structures and to consider that the structure of $\mathrm{CO}_2$ is best described as a hybrid of the canonical or resonance forms I, II and III.

Fig. 4.5 Resonance in $\mathrm{CO}_{2}$ molecule, I, II and III represent the three canonical forms.
In general, it may be stated that
- Resonance stabilizes the molecule as the energy of the resonance hybrid is less than the energy of any single cannonical structure; and,
- Resonance averages the bond characteristics as a whole.
Thus the energy of the $\mathrm{O}_{3}$ resonance hybrid is lower than either of the two cannonical froms I and II (Fig. 4.3).
Many misconceptions are associated with resonance and the same need to be dispelled. You should remember that:
- The cannonical forms have no real existence.
- The molecule does not exist for a certain fraction of time in one cannonical form and for other fractions of time in other cannonical forms.
- There is no such equilibrium between the cannonical forms as we have between tautomeric forms (keto and enol) in tautomerism.
- The molecule as such has a single structure which is the resonance hybrid of the cannonical forms and which cannot as such be depicted by a single Lewis structure.
4.3.6 Polarity of Bonds
The existence of a hundred percent ionic or covalent bond represents an ideal situation. In reality no bond or a compound is either completely covalent or ionic. Even in case of covalent bond between two hydrogen atoms, there is some ionic character.
When covalent bond is formed between two similar atoms, for example in $\mathrm{H}_2, \mathrm{O}_2$, $\mathrm{Cl}_2, \mathrm{~N}_2$ or $\mathrm{F}_2$, the shared pair of electrons is equally attracted by the two atoms. As a result electron pair is situated exactly between the two identical nuclei. The bond so formed is called nonpolar covalent bond. Contrary to this in case of a heteronuclear molecule like $\mathrm{HF}$, the shared electron pair between the two atoms gets displaced more towards fluorine since the electronegativity of fluorine (Unit 3) is far greater than that of hydrogen. The resultant covalent bond is a polar covalent bond.
As a result of polarisation, the molecule possesses the dipole moment (depicted below) which can be defined as the product of the magnitude of the charge and the distance between the centres of positive and negative charge. It is usually designated by a Greek letter ’ $\mu$ ‘. Mathematically, it is expressed as follows :
Dipole moment $(\mu)=$ charge $(Q) \times$ distance of separation ( $\mathrm{r}$ )
Dipole moment is usually expressed in Debye units (D). The conversion factor is
$$ 1 \mathrm{D}=3.33564 \times 10^{-30} \mathrm{C} \mathrm{m} $$
where $\mathrm{C}$ is coulomb and $\mathrm{m}$ is meter.
Further dipole moment is a vector quantity and by convention it is depicted by a small arrow with tail on the negative centre and head pointing towards the positive centre. But in chemistry presence of dipole moment is represented by the crossed arrow $(\rightarrow)$ put on Lewis structure of the molecule. The cross is on positive end and arrow head is on negative end. For example the dipole moment of HF may be represented as :
$$ \stackrel{+}{\mathrm{H} \longrightarrow} \underset{\because}{*}: $$
This arrow symbolises the direction of the shift of electron density in the molecule. Note that the direction of crossed arrow is opposite to the conventional direction of dipole moment vector
Peter Debye, the Dutch chemist received Nobel prize in 1936 for his work on X-ray diffraction and dipole moments. The magnitude of the dipole moment is given in Debye units in order to honour him.

In case of polyatomic molecules the dipole moment not only depend upon the individual dipole moments of bonds known as bond dipoles but also on the spatial arrangement of various bonds in the molecule. In such case, the dipole moment of a molecule is the vector sum of the dipole moments of various bonds. For example in $\mathrm{H}_{2} \mathrm{O}$ molecule, which has a bent structure, the two $\mathrm{O}-\mathrm{H}$ bonds are oriented at an angle of $104.5^{\circ}$. Net dipole moment of $6.17 \times 10^{-30} \mathrm{C} \mathrm{m} \mathrm{(1D} \mathrm{=} 3.33564$ $\times 10^{-30} \mathrm{C} \mathrm{m}$ ) is the resultant of the dipole moments of two $\mathrm{O}-\mathrm{H}$ bonds.
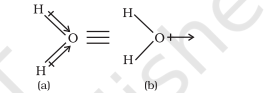
Net Dipole moment, $\mu=1.85 \mathrm{D}$
$=1.85 \times 3.33564 \times 10^{-30} \mathrm{C} \mathrm{m}=6.17 \times 10^{-30} \mathrm{C} \mathrm{m}$
The dipole moment in case of $\mathrm{BeF}_{2}$ is zero. This is because the two equal bond dipoles point in opposite directions and cancel the effect of each other.

In tetra-atomic molecule, for example in $\mathrm{BF}_{3}$, the dipole moment is zero although the $\mathrm{B}-\mathrm{F}$ bonds are oriented at an angle of $120^{\circ}$ to one another, the three bond moments give a net sum of zero as the resultant of any two is equal and opposite to the third.
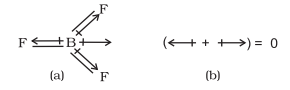
$\mathrm{BF}_3$ molecule; representation of (a) bond dipoles and (b) total dipole moment
Let us study an interesting case of $\mathrm{NH}_3$ and $\mathrm{NF}_3$ molecule. Both the molecules have pyramidal shape with a lone pair of electrons on nitrogen atom. Although fluorine is more electronegative than nitrogen, the resultant dipole moment of $\mathrm{NH}_3\left(4.90 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$ is greater than that of $\mathrm{NF}_3\left(0.8 \times 10^{-30} \mathrm{C} \mathrm{m}\right)$. This is because, in case of $\mathrm{NH}_3$ the orbital dipole due to lone pair is in the same direction as the resultant dipole moment of the $\mathrm{N}-\mathrm{H}$ bonds, whereas in $\mathrm{NF}_3$ the orbital dipole is in the direction opposite to the resultant dipole moment of the three N-F bonds. The orbital dipole because of lone pair decreases the effect of the resultant $\mathrm{N}-\mathrm{F}$ bond moments, which results in the low dipole moment of $\mathrm{NF}_3$ as represented below :

Dipole moments of some molecules are shown in Table 4.5.
Just as all the covalent bonds have some partial ionic character, the ionic bonds also have partial covalent character. The partial covalent character of ionic bonds was discussed by Fajans in terms of the following rules:
- The smaller the size of the cation and the larger the size of the anion, the greater the covalent character of an ionic bond.
- The greater the charge on the cation, the greater the covalent character of the ionic bond.
- For cations of the same size and charge, the one, with electronic configuration $(n-1) d^{n} n s^{\circ}$, typical of transition metals, is more polarising than the one with a noble gas configuration, $n s^{2} n p^{6}$, typical of alkali and alkaline earth metal cations.
The cation polarises the anion, pulling the electronic charge toward itself and thereby increasing the electronic charge between the two. This is precisely what happens in a covalent bond, i.e., buildup of electron charge density between the nuclei. The polarising power of the cation, the polarisability of the anion and the extent of distortion (polarisation) of anion are the factors, which determine the per cent covalent character of the ionic bond.
4.4 THE VALENCE SHELL ELECTRON PAIR REPULSION (VSEPR) THEORY
As already explained, Lewis concept is unable to explain the shapes of molecules. This theory provides a simple procedure to predict the shapes of covalent molecules. Sidgwick and Powell in 1940, proposed a simple theory based on the repulsive interactions of the electron pairs in the valence shell of the atoms. It was further developed and redefined by Nyholm and Gillespie (1957).
Table 4.5 Dipole Moments of Selected Molecules
| Type of Molecule | Example | Dipole Moment, $\boldsymbol{\mu}(\mathbf{D})$ |
Geometry |
|---|---|---|---|
| Molecule $(\mathbf{A B})$ | $\mathrm{HF}$ | 1.78 | linear |
| $\mathrm{HCl}$ | 1.07 | linear | |
| $\mathrm{HBr}$ | 0.79 | linear | |
| $\mathrm{Hl}$ | 0.38 | linear | |
| $\mathrm{H}_{2}$ | 0 | linear | |
| Molecule $\left(\mathbf{A B}_{\mathbf{2}}\right)$ | $\mathrm{H}_{2} \mathrm{O}$ | 1.85 | bent |
| $\mathrm{H}_{2} \mathrm{~S}$ | 0.95 | bent | |
| $\mathrm{CO}_{2}$ | 0 | linear | |
| Molecule $\left(\mathbf{A B}_{3}\right)$ | $\mathrm{NH}_{3}$ | 1.47 | trigonal-pyramidal |
| $\mathrm{NF}_{3}$ | 0.23 | trigonal-pyramidal | |
| $\mathrm{BF}_{3}$ | 0 | trigonal-planar | |
| Molecule $\left(\mathbf{A B}_{\mathbf{4}}\right)$ | $\mathrm{CH}_{4}$ | 0 | tetrahedral |
| $\mathrm{CHCl}_{3}$ | 1.04 | tetrahedral | |
| $\mathrm{CCl}_{4}$ | 0 | tetrahedral |
The main postulates of VSEPR theory are as follows:
- The shape of a molecule depends upon the number of valence shell electron pairs (bonded or nonbonded) around the central atom.
- Pairs of electrons in the valence shell repel one another since their electron clouds are negatively charged.
- These pairs of electrons tend to occupy such positions in space that minimise repulsion and thus maximise distance between them.
- The valence shell is taken as a sphere with the electron pairs localising on the spherical surface at maximum distance from one another.
- A multiple bond is treated as if it is a single electron pair and the two or three electron pairs of a multiple bond are treated as a single super pair.
- Where two or more resonance structures can represent a molecule, the VSEPR model is applicable to any such structure.
The repulsive interaction of electron pairs decrease in the order:
Lone pair (lp) - Lone pair (lp) > Lone pair (lp) - Bond pair (bp) > Bond pair (bp) Bond pair (bp)
Nyholm and Gillespie (1957) refined the VSEPR model by explaining the important difference between the lone pairs and bonding pairs of electrons. While the lone pairs are localised on the central atom, each bonded pair is shared between two atoms. As a result, the lone pair electrons in a molecule occupy more space as compared to the bonding pairs of electrons. This results in greater repulsion between lone pairs of electrons as compared to the lone pair - bond pair and bond pair bond pair repulsions. These repulsion effects result in deviations from idealised shapes and alterations in bond angles in molecules.
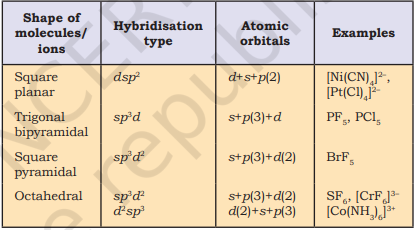
For the prediction of geometrical shapes of molecules with the help of VSEPR theory, it is convenient to divide molecules into two categories as (i) molecules in which the central atom has no lone pair and (ii) molecules in which the central atom has one or more lone pairs.
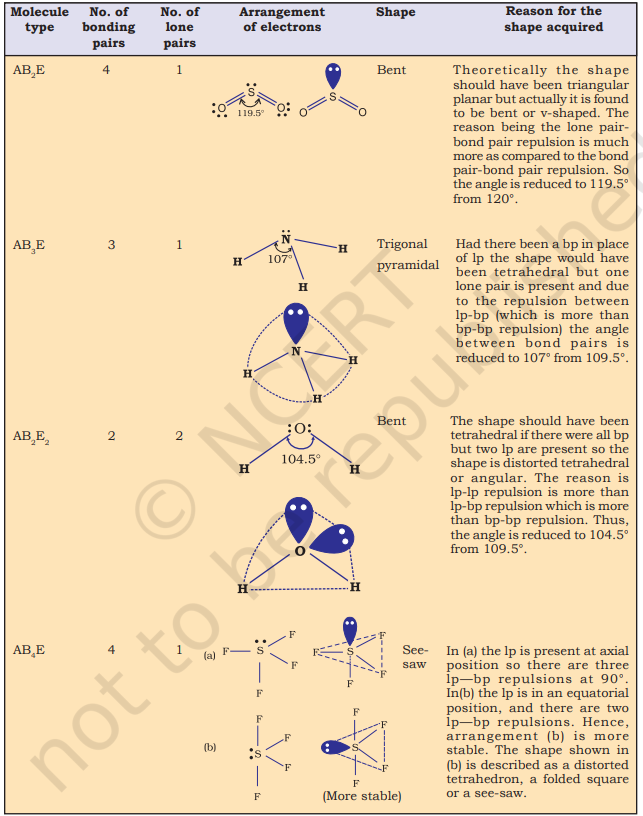
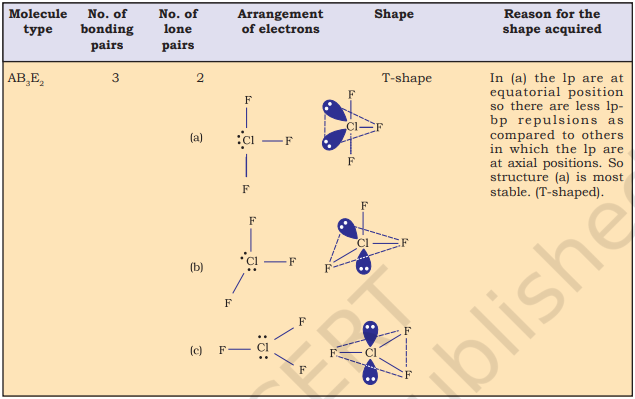
Table 4.6 (page114) shows the arrangement of electron pairs about a central atom A (without any lone pairs) and geometries of some molecules/ions of the type AB. Table 4.7 (page 115) shows shapes of some simple molecules and ions in which the central atom has one or more lone pairs. Table 4.8 (page 116) explains the reasons for the distortions in the geometry of the molecule.
As depicted in Table 4.6, in the compounds of $\mathrm{AB}_2, \mathrm{AB}_3, \mathrm{AB}_4, \mathrm{AB}_5$ and $\mathrm{AB}_6$, the arrangement of electron pairs and the $\mathrm{B}$ atoms around the central atom A are : linear, trigonal planar, tetrahedral, trigonal-bipyramidal and octahedral, respectively. Such arrangement can be seen in the molecules like $\mathrm{BF}_3\left(\mathrm{AB}_3\right), \mathrm{CH}_4\left(\mathrm{AB}_4\right)$ and $\mathrm{PCl}_5\left(\mathrm{AB}_5\right)$ as depicted below by their ball and stick models.
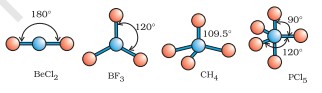
Fig. 4.8 The shapes of molecules in which central atom has no lone pair
The VSEPR Theory is able to predict geometry of a large number of molecules, especially the compounds of $p$-block elements accurately. It is also quite successful in determining the geometry quite-accurately even when the energy difference between possible structures is very small. The theoretical basis of the VSEPR theory regarding the effects of electron pair repulsions on molecular shapes is not clear and continues to be a subject of doubt and discussion.
Table 4.6 Geometry of Molecules in which the Central Atom has No Lone Pair of Electrons
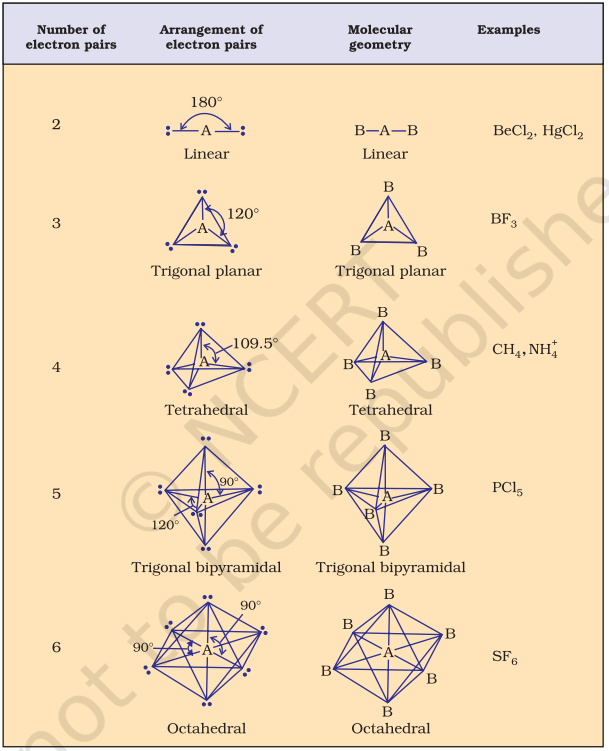
Table 4.7 Shape (geometry) of Some Simple Molecules/Ions with Central Ions having One or More Lone Pairs of Electrons(E)
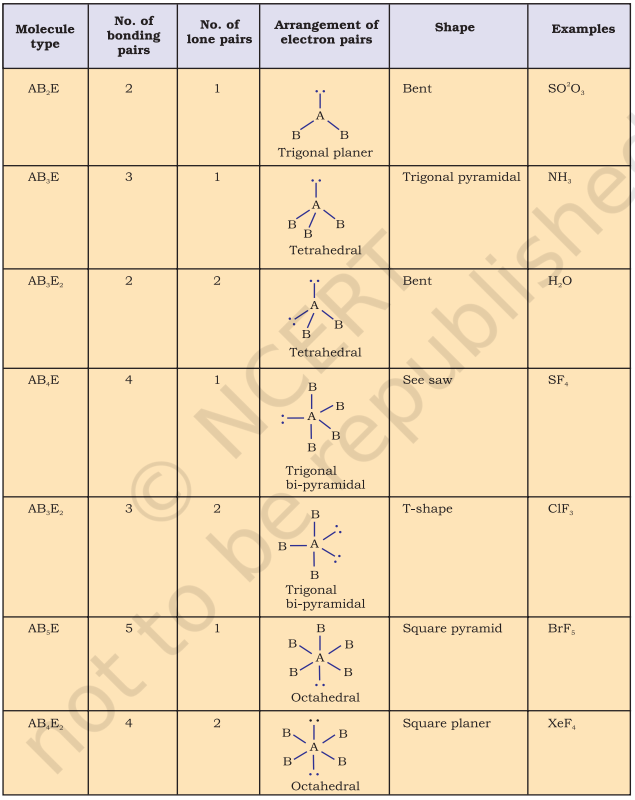
Table 4.8 Shapes of Molecules containing Bond Pair and Lone Pair
4.5 VALENCE BOND THEORY
As we know that Lewis approach helps in writing the structure of molecules but it fails to explain the formation of chemical bond. It also does not give any reason for the difference in bond dissociation enthalpies and bond lengths in molecules like $\mathrm{H}_2(435.8 \mathrm{~kJ}$ $\left.\mathrm{mol}^{-1}, 74 \mathrm{pm}\right)$ and $\mathrm{F}_2\left(155 \mathrm{~kJ} \mathrm{~mol}^{-1}, 144 \mathrm{pm}\right)$, although in both the cases a single covalent bond is formed by the sharing of an electron pair between the respective atoms. It also gives no idea about the shapes of polyatomic molecules.
Similarly the VSEPR theory gives the geometry of simple molecules but theoretically, it does not explain them and also it has limited applications. To overcome these limitations the two important theories based on quantum mechanical principles are introduced. These are valence bond (VB) theory and molecular orbital (MO) theory.
Valence bond theory was introduced by Heitler and London (1927) and developed further by Pauling and others. A discussion of the valence bond theory is based on the knowledge of atomic orbitals, electronic configurations of elements (Units 2), the overlap criteria of atomic orbitals, the hybridization of atomic orbitals and the principles of variation and superposition. A rigorous treatment of the VB theory in terms of these aspects is beyond the scope of this book. Therefore, for the sake of convenience, valence bond theory has been discussed in terms of qualitative and non-mathematical treatment only. To start with, let us consider the formation of hydrogen molecule which is the simplest of all molecules.
Consider two hydrogen atoms A and B approaching each other having nuclei $\mathrm{N}_{\mathrm{A}}$ and $N_B$ and electrons present in them are represented by $e_A$ and $e_B$. When the two atoms are at large distance from each other, there is no interaction between them. As these two atoms approach each other, new attractive and repulsive forces begin to operate.
Attractive forces arise between:
(i) nucleus of one atom and its own electron that is $N_{A}-e_{A}$ and $N_{B}-e_{B}$.
(ii) nucleus of one atom and electron of other atom i.e., $N_{A}-e_{B}, N_{B}-e_{A}$.
Similarly repulsive forces arise between
(i) electrons of two atoms like $e_{A}-e_{B}$,
(ii) nuclei of two atoms $N_{A}-N_{B}$.
Attractive forces tend to bring the two atoms close to each other whereas repulsive forces tend to push them apart (Fig. 4.7).

Fig. 4.7 Forces of attraction and repulsion during the formation of H2 molecule
Experimentally it has been found that the magnitude of new attractive force is more than the new repulsive forces. As a result, two atoms approach each other and potential energy decreases. Ultimately a stage is reached where the net force of attraction balances the force of repulsion and system acquires minimum energy. At this stage two hydrogen atoms are said to be bonded together to form a stable molecule having the bond length of $74 \mathrm{pm}$.
Since the energy gets released when the bond is formed between two hydrogen atoms, the hydrogen molecule is more stable than that of isolated hydrogen atoms. The energy so released is called as bond enthalpy, which is corresponding to minimum in the curve depicted in Fig. 4.8. Conversely, $435.8 \mathrm{~kJ}$ of energy is required to dissociate one mole of $\mathrm{H}_{2}$ molecule.
$\mathrm{H}_{2}(\mathrm{~g})+435.8 \mathrm{~kJ} \mathrm{~mol}^{-1} \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$

Fig. 4.8 The potential energy curve for the formation of H2 molecule as a function of internuclear distance of the H atoms. The minimum in the curve corresponds to the most stable state of $H_2$.
4.5.1 Orbital Overlap Concept
In the formation of hydrogen molecule, there is a minimum energy state when two hydrogen atoms are so near that their atomic orbitals undergo partial interpenetration. This partial merging of atomic orbitals is called overlapping of atomic orbitals which results in the pairing of electrons. The extent of overlap decides the strength of a covalent bond. In general, greater the overlap the stronger is the bond formed between two atoms. Therefore, according to orbital overlap concept, the formation of a covalent bond between two atoms results by pairing of electrons present in the valence shell having opposite spins.
4.5.2 Directional Properties of Bonds
As we have already seen, the covalent bond is formed by overlapping of atomic orbitals. The molecule of hydrogen is formed due to the overlap of $1 s$-orbitals of two $\mathrm{H}$ atoms.
In case of polyatomic molecules like $\mathrm{CH}_4$, $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$, the geometry of the molecules is also important in addition to the bond formation. For example why is it so that $\mathrm{CH}_4$ molecule has tetrahedral shape and $\mathrm{HCH}$ bond angles are $109.5^{\circ}$ ? Why is the shape of $\mathrm{NH}_3$ molecule pyramidal ?
The valence bond theory explains the shape, the formation and directional properties of bonds in polyatomic molecules like $\mathrm{CH}_4$, $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$, etc. in terms of overlap and hybridisation of atomic orbitals.
4.5.3 Overlapping of Atomic Orbitals
When orbitals of two atoms come close to form bond, their overlap may be positive, negative or zero depending upon the sign (phase) and direction of orientation of amplitude of orbital wave function in space (Fig. 4.9). Positive and negative sign on boundary surface diagrams in the Fig. 4.9 show the sign (phase) of orbital wave function and are not related to charge. Orbitals forming bond should have same sign (phase) and orientation in space. This is called positive overlap. Various overlaps of $s$ and $p$ orbitals are depicted in Fig. 4.9.
The criterion of overlap, as the main factor for the formation of covalent bonds applies uniformly to the homonuclear/heteronuclear diatomic molecules and polyatomic molecules. We know that the shapes of $\mathrm{CH}_4, \mathrm{NH}_3$, and $\mathrm{H}_2 \mathrm{O}$ molecules are tetrahedral, pyramidal and bent respectively. It would be therefore interesting to use VB theory to find out if these geometrical shapes can be explained in terms of the orbital overlaps.
Let us first consider the $CH_4$ (methane) molecule. The electronic configuration of carbon in its ground state is $[\mathrm{He}] 2 s^2 2 p^2$ which in the excited state becomes $[\mathrm{He}] 2 s^1 2 p_{\mathrm{x}}^1$ $2 p_{\mathrm{y}}^1$ $2 p_z^1$. The energy required for this excitation is compensated by the release of energy due to overlap between the orbitals of carbon and the hydrogen.
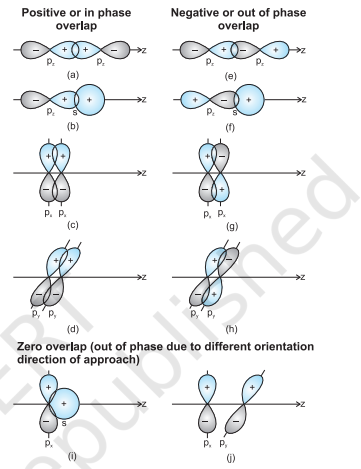
Fig.4.9 Positive, negative and zero overlaps of s and p atomic orbitals
The four atomic orbitals of carbon, each with an unpaired electron can overlap with the $1 \mathrm{~s}$ orbitals of the four $\mathrm{H}$ atoms which are also singly occupied. This will result in the formation of four $\mathrm{C}-\mathrm{H}$ bonds. It will, however, be observed that while the three $\mathrm{p}$ orbitals of carbon are at $90^{\circ}$ to one another, the $\mathrm{HCH}$ angle for these will also be $90^{\circ}$. That is three $\mathrm{C}-\mathrm{H}$ bonds will be oriented at $90^{\circ}$ to one another. The $2 \mathrm{~s}$ orbital of carbon and the $1 \mathrm{~s}$ orbital of $\mathrm{H}$ are spherically symmetrical and they can overlap in any direction. Therefore the direction of the fourth $\mathrm{C}-\mathrm{H}$ bond cannot be ascertained. This description does not fit in with the tetrahedral $\mathrm{HCH}$ angles of $109.5^{\circ}$. Clearly, it follows that simple atomic orbital overlap does not account for the directional characteristics of bonds in $\mathrm{CH}_4$. Using similar procedure and arguments, it can be seen that in the case of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules, the $\mathrm{HNH}$ and $\mathrm{HOH}$ angles should be $90^{\circ}$. This is in disagreement with the actual bond angles of $107^{\circ}$ and $104.5^{\circ}$ in the $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules respectively.
4.5.4 Types of Overlapping and Nature of Covalent Bonds
The covalent bond may be classified into two types depending upon the types of overlapping:
(i) Sigma( $\sigma$ ) bond, and (ii) pi( $\pi$ ) bond
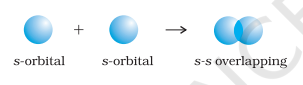
(i) Sigma( $\sigma$ ) bond : This type of covalent bond is formed by the end to end (headon) overlap of bonding orbitals along the internuclear axis. This is called as head on overlap or axial overlap. This can be formed by any one of the following types of combinations of atomic orbitals.
- s-s overlapping : In this case, there is overlap of two half filled s-orbitals along the internuclear axis as shown below :
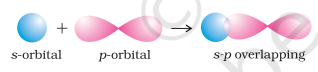
- s-p overlapping: This type of overlap occurs between half filled $s$-orbitals of one atom and half filled $p$-orbitals of another atom.
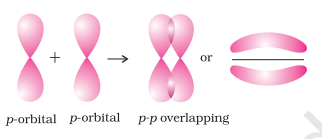
- $\boldsymbol{p}-\boldsymbol{p}$ overlapping : This type of overlap takes place between half filled $p$-orbitals of the two approaching atoms.

(ii) pi( $\pi$ ) bond : In the formation of $\pi$ bond the atomic orbitals overlap in such a way that their axes remain parallel to each other and perpendicular to the internuclear axis. The orbitals formed due to sidewise overlapping consists of two saucer type charged clouds above and below the plane of the participating atoms.
4.5.5 Strength of Sigma and pi Bonds
Basically the strength of a bond depends upon the extent of overlapping. In case of sigma bond, the overlapping of orbitals takes place to a larger extent. Hence, it is stronger as compared to the pi bond where the extent of overlapping occurs to a smaller extent. Further, it is important to note that in the formation of multiple bonds between two atoms of a molecule, pi bond(s) is formed in addition to a sigma bond.
4.6 HYBRIDISATION
In order to explain the characteristic geometrical shapes of polyatomic molecules like $\mathrm{CH}_4, \mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ etc., Pauling introduced the concept of hybridisation. According to him the atomic orbitals combine to form new set of equivalent orbitals known as hybrid orbitals. Unlike pure orbitals, the hybrid orbitals are used in bond formation. The phenomenon is known as hybridisation which can be defined as the process of intermixing of the orbitals of slightly different energies so as to redistribute their energies, resulting in the formation of new set of orbitals of equivalent energies and shape. For example when one $2 s$ and three $2 p$-orbitals of carbon hybridise, there is the formation of four new $s p^{3}$ hybrid orbitals.
Salient features of hybridisation: The main features of hybridisation are as under :
1. The number of hybrid orbitals is equal to the number of the atomic orbitals that get hybridised.
2. The hybridised orbitals are always equivalent in energy and shape.
3. The hybrid orbitals are more effective in forming stable bonds than the pure atomic orbitals.
4. These hybrid orbitals are directed in space in some preferred direction to have minimum repulsion between electron pairs and thus a stable arrangement. Therefore, the type of hybridisation indicates the geometry of the molecules.
Important conditions for hybridisation
(i) The orbitals present in the valence shell of the atom are hybridised.
(ii) The orbitals undergoing hybridisation should have almost equal energy.
(iii) Promotion of electron is not essential condition prior to hybridisation.
(iv) It is not necessary that only half filled orbitals participate in hybridisation. In some cases, even filled orbitals of valence shell take part in hybridisation.
4.6.1 Types of Hybridisation
There are various types of hybridisation involving $s, p$ and $d$ orbitals. The different types of hybridisation are as under:
(I) sp hybridisation: This type of hybridisation involves the mixing of one $s$ and one $p$ orbital resulting in the formation of two equivalent $s p$ hybrid orbitals. The suitable orbitals for $s p$ hybridisation are $s$ and $p_{z}$, if the hybrid orbitals are to lie along the $z$-axis. Each $s p$ hybrid orbitals has $50 %$ s-character and $50 % p$-character. Such a molecule in which the central atom is $s p$-hybridised and linked directly to two other central atoms possesses linear geometry. This type of hybridisation is also known as diagonal hybridisation.
The two $s p$ hybrids point in the opposite direction along the $z$-axis with projecting positive lobes and very small negative lobes, which provides more effective overlapping resulting in the formation of stronger bonds.
Example of molecule having $s p$ hybridisation
$\mathbf{B e C l}_{2}$ : The ground state electronic configuration of Be is $1 s^{2} 2 s^{2}$. In the exited state one of the $2 \mathrm{~s}$-electrons is promoted to vacant $2 p$ orbital to account for its bivalency. One $2 s$ and one $2 p$-orbital gets hybridised to form two $s p$ hybridised orbitals. These two $s p$ hybrid orbitals are oriented in opposite direction forming an angle of $180^{\circ}$. Each of the $s p$ hybridised orbital overlaps with the $2 p$-orbital of chlorine axially and form two Be$\mathrm{Cl}$ sigma bonds. This is shown in Fig. 4.10.
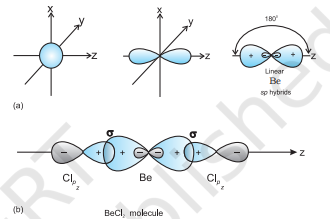
Fig.4.10 (a) Formation of sp hybrids from s and p orbitals; (b) Formation of the linear $BeCl_2$ molecule
(II) $\boldsymbol{s p}^{2}$ hybridisation : In this hybridisation there is involvement of one $s$ and two $p$-orbitals in order to form three equivalent $s p^{2}$ hybridised orbitals. For example, in $\mathrm{BCl} _{3}$ molecule, the ground state electronic configuration of central boron atom is $1 s^{2} 2 s^{2} 2 p^{1}$. In the excited state, one of the $2 s$ electrons is promoted to vacant $2 p$ orbital as a result boron has three unpaired electrons. These three orbitals (one $2 s$ and two $2 p$ ) hybridise to form three $s p^{2}$ hybrid orbitals. The three hybrid orbitals so formed are oriented in a trigonal planar arrangement and overlap with $2 p$ orbitals of chlorine to form three $\mathrm{B}-\mathrm{Cl}$ bonds. Therefore, in $\mathrm{BCl} _{3}$ (Fig. 4.11), the geometry is trigonal planar with $\mathrm{ClBCl}$ bond angle of $120^{\circ}$.
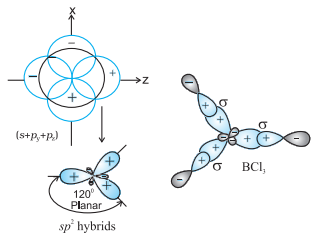
Fig.4.11 Formation of $sp_2$ hybrids and the $BCl_3$ molecule
(III) $\boldsymbol{s p}^{3}$ hybridisation: This type of hybridisation can be explained by taking the example of $\mathrm{CH}_{4}$ molecule in which there is mixing of one s-orbital and three $p$-orbitals of the valence shell to form four $s p^{3}$ hybrid orbital of equivalent energies and shape. There is $25 % s$-character and $75 % p$-character in each $s p^{3}$ hybrid orbital. The four $s p^{3}$ hybrid orbitals so formed are directed towards the four corners of the tetrahedron. The angle between $s p^{3}$ hybrid orbital is $109.5^{\circ}$ as shown in Fig. 4.12.
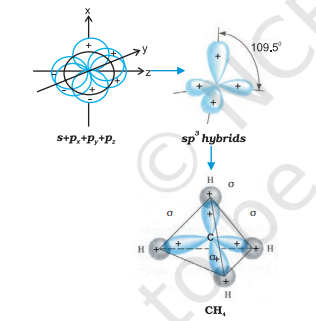
Fig.4.12 Formation of sp3 hybrids by the combination of s, $p_x$, $p_y$ and $p_z$ atomic orbitals of carbon and the formation of $CH_4$ molecule
The structure of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules can also be explained with the help of $s p^{3}$ hybridisation. In $\mathrm{NH}_3$, the valence shell (outer) electronic configuration of nitrogen in the ground state is $2 S^{2} 2 p_x^{1} 2 p_y^{1} 2 p_z^{1}$ having three unpaired electrons in the $s p^{3}$ hybrid orbitals and a lone pair of electrons is present in the fourth one. These three hybrid orbitals overlap with $1 \mathrm{~s}$ orbitals of hydrogen atoms to form three $\mathrm{N}-\mathrm{H}$ sigma bonds. We know that the force of repulsion between a lone pair and a bond pair is more than the force of repulsion between two bond pairs of electrons. The molecule thus gets distorted and the bond angle is reduced to $107^{\circ}$ from $109.5^{\circ}$. The geometry of such a molecule will be pyramidal as shown in Fig. 4.13.
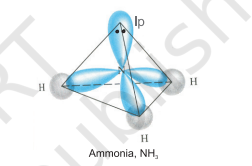
Fig.4.13 Formation of $NH_3$ molecule
In case of $\mathrm{H}_{2} \mathrm{O}$ molecule, the four oxygen orbitals (one $2 s$ and three $2 p$ ) undergo $s p^{3}$ hybridisation forming four $s p^{3}$ hybrid orbitals out of which two contain one electron each and the other two contain a pair of electrons. These four $s p^{3}$ hybrid orbitals acquire a tetrahedral geometry, with two corners occupied by hydrogen atoms while the other two by the lone pairs. The bond angle in this case is reduced to $104.5^{\circ}$ from $109.5^{\circ}$ (Fig. 4.14) and the molecule thus acquires a V-shape or angular geometry.
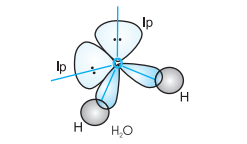
Fig.4.14 Formation of $H_2 O$ molecule
4.6.2 Other Examples of $s p^{3}, s p^{2}$ and $s p$ Hybridisation
sp $^{3}$ Hybridisation in $\mathrm{C}_2 \mathrm{H}_6$ molecule: In ethane molecule both the carbon atoms assume $s p^{3}$ hybrid state. One of the four $s p^{3}$ hybrid orbitals of carbon atom overlaps axially with similar orbitals of other atom to form $s p^{3}-s p^{3}$ sigma bond while the other three hybrid orbitals of each carbon atom are used in forming $s p^{3}-s$ sigma bonds with hydrogen atoms as discussed in section 4.6.1(iii). Therefore in ethane $\mathrm{C}-\mathrm{C}$ bond length is 154 $\mathrm{pm}$ and each $\mathrm{C}-\mathrm{H}$ bond length is $109 \mathrm{pm}$.
$\boldsymbol{s p}^{2}$ Hybridisation in $\mathbf{C}_2 \boldsymbol{H}_4$ : In the formation of ethene molecule, one of the $s p^2$ hybrid orbitals of carbon atom overlaps axially with $s p^2$ hybridised orbital of another carbon atom to form $\mathrm{C}-\mathrm{C}$ sigma bond. While the other two $s p^{2}$ hybrid orbitals of each carbon atom are used for making $s p^2-s$ sigma bond with two hydrogen atoms. The unhybridised orbital ($2 p_x$ or $2 p_y$ ) of one carbon atom overlaps sidewise with the similar orbital of the other carbon atom to form weak $\pi$ bond, which consists of two equal electron clouds distributed above and below the plane of carbon and hydrogen atoms.
Thus, in ethene molecule, the carboncarbon bond consists of one $s p^{2}-s p^{2}$ sigma bond and one pi $(\pi)$ bond between $p$ orbitals which are not used in the hybridisation and are perpendicular to the plane of molecule; the bond length $134 \mathrm{pm}$. The $\mathrm{C}-\mathrm{H}$ bond is $s p^{2}-\mathrm{s}$ sigma with bond length $108 \mathrm{pm}$. The $\mathrm{H}-\mathrm{C}-\mathrm{H}$ bond angle is $117.6^{\circ}$ while the $\mathrm{H}-\mathrm{C}-\mathrm{C}$ angle is $121^{\circ}$. The formation of sigma and pi bonds in ethene is shown in Fig. 4.15.
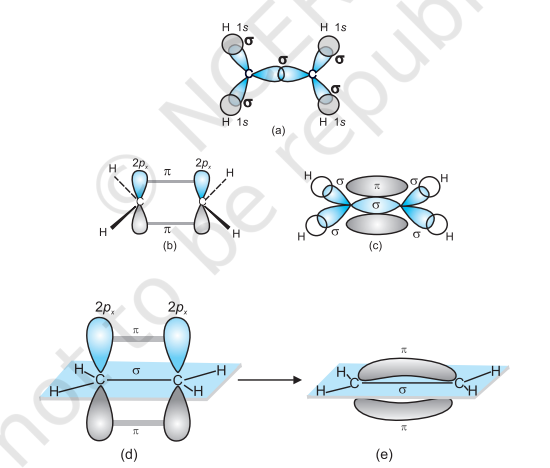
Fig. 4.15 Formation of sigma and pi bonds in ethene
sp Hybridisation in $\mathbf{C}_2 \mathbf{H}_2$ : In the formation of ethyne molecule, both the carbon atoms undergo $s p$-hybridisation having two unhybridised orbital i.e., $2 p_y$ and $2 p_x$.
One $s p$ hybrid orbital of one carbon atom overlaps axially with $s p$ hybrid orbital of the other carbon atom to form $\mathrm{C}-\mathrm{C}$ sigma bond, while the other hybridised orbital of each carbon atom overlaps axially with the half filled $s$ orbital of hydrogen atoms forming $\sigma$ bonds. Each of the two unhybridised $p$ orbitals of both the carbon atoms overlaps sidewise to form two $\pi$ bonds between the carbon atoms. So the triple bond between the two carbon atoms is made up of one sigma and two pi bonds as shown in Fig. 4.16.

Fig.4.16 Formation of sigma and pi bonds in ethyne
4.6.3 Hybridisation of Elements involving d Orbitals
The elements present in the third period contain $d$ orbitals in addition to $s$ and $p$ orbitals. The energy of the $3 d$ orbitals are comparable to the energy of the $3 s$ and $3 p$ orbitals. The energy of $3 d$ orbitals are also comparable to those of $4 s$ and $4 p$ orbitals. As a consequence the hybridisation involving either $3 s, 3 p$ and $3 d$ or $3 d, 4 s$ and $4 p$ is possible. However, since the difference in energies of $3 p$ and $4 s$ orbitals is significant, no hybridisation involving $3 p, 3 d$ and $4 s$ orbitals is possible.
The important hybridisation schemes involving $s, p$ and $d$ orbitals are summarised below:
(i) Formation of $\mathrm{PCl}_{5}\left(\mathrm{sp}^{3} \mathrm{~d}\right.$ hybridisation): The ground state and the excited state outer electronic configurations of phosphorus $(Z=15)$ are represented below.
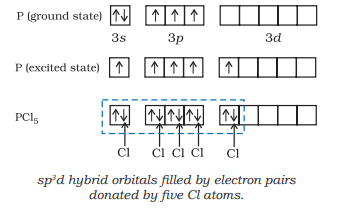
Now the five orbitals (i.e., one $s$, three $p$ and one $d$ orbitals) are available for hybridisation to yield a set of five $s p^{3} d$ hybrid orbitals which are directed towards the five corners of a trigonal bipyramidal as depicted in the Fig. 4.17.
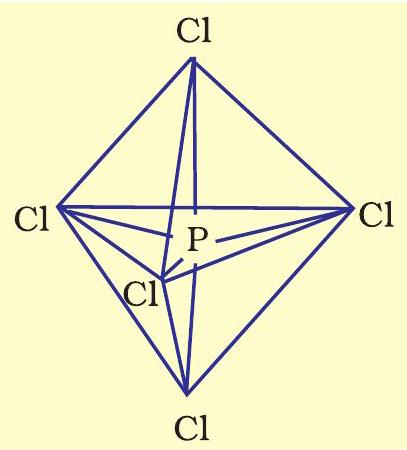
Fig. 4.17 Trigonal bipyramidal geometry of $PCl_5$ molecule
It should be noted that all the bond angles in trigonal bipyramidal geometry are not equivalent. In $\mathrm{PCl}_5$ the five $s p^{3} d$ orbitals of phosphorus overlap with the singly occupied $p$ orbitals of chlorine atoms to form five $\mathrm{P}-\mathrm{Cl}$ sigma bonds. Three $\mathrm{P}-\mathrm{Cl}$ bond lie in one plane and make an angle of $120^{\circ}$ with each other; these bonds are termed as equatorial bonds. The remaining two $\mathrm{P}-\mathrm{Cl}$ bonds-one lying above and the other lying below the equatorial plane, make an angle of $90^{\circ}$ with the plane. These bonds are called axial bonds. As the axial bond pairs suffer more repulsive interaction from the equatorial bond pairs, therefore axial bonds have been found to be slightly longer and hence slightly weaker than the equatorial bonds; which makes $\mathrm{PCl}_5$ molecule more reactive.
(ii) Formation of $\mathbf{S F}_6\left(\mathrm{sp}^{3} d^{2}\right.$ hybridisation): In $\mathrm{SF}_6$ the central sulphur atom has the ground state outer electronic configuration $3 s^{2} 3 p^{4}$. In the exited state the available six orbitals i.e., one s, three $p$ and two $d$ are singly occupied by electrons. These orbitals hybridise to form six new $s p^{3} d^{2}$ hybrid orbitals, which are projected towards the six corners of a regular octahedron in $\mathrm{SF}_6$. These six $s p^{3} d^{2}$ hybrid orbitals overlap with singly occupied orbitals of fluorine atoms to form six $\mathrm{S}-\mathrm{F}$ sigma bonds. Thus $\mathrm{SF}_6$ molecule has a regular octahedral geometry as shown in Fig. 4.18.
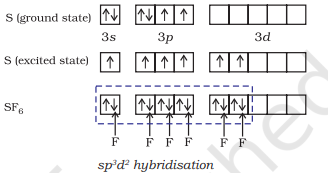
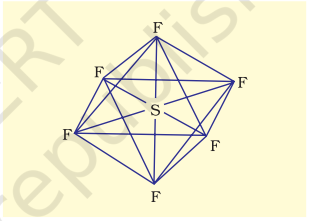
Fig. 4.18 Octahedral geometry of SF6 molecule
4.7 MOLECULAR ORBITAL THEORY
Molecular orbital (MO) theory was developed by F. Hund and R.S. Mulliken in 1932. The salient features of this theory are :
(i) The electrons in a molecule are present in the various molecular orbitals as the electrons of atoms are present in the various atomic orbitals.
(ii) The atomic orbitals of comparable energies and proper symmetry combine to form molecular orbitals.
(iii) While an electron in an atomic orbital is influenced by one nucleus, in a molecular orbital it is influenced by two or more nuclei depending upon the number of atoms in the molecule. Thus, an atomic orbital is monocentric while a molecular orbital is polycentric.
(iv) The number of molecular orbital formed is equal to the number of combining atomic orbitals. When two atomic orbitals combine, two molecular orbitals are formed. One is known as bonding molecular orbital while the other is called antibonding molecular orbital.
(v) The bonding molecular orbital has lower energy and hence greater stability than the corresponding antibonding molecular orbital.
(vi) Just as the electron probability distribution around a nucleus in an atom is given by an atomic orbital, the electron probability distribution around a group of nuclei in a molecule is given by a molecular orbital.
(vii) The molecular orbitals like atomic orbitals are filled in accordance with the aufbau principle obeying the Pauli’s exclusion principle and the Hund’s rule.
4.7.1 Formation of Molecular Orbitals Linear Combination of Atomic Orbitals (LCAO)
According to wave mechanics, the atomic orbitals can be expressed by wave functions ( $\psi$ ’s) which represent the amplitude of the electron waves. These are obtained from the solution of Schrödinger wave equation. However, since it cannot be solved for any system containing more than one electron, molecular orbitals which are one electron wave functions for molecules are difficult to obtain directly from the solution of Schrödinger wave equation. To overcome this problem, an approximate method known as linear combination of atomic orbitals (LCAO) has been adopted.
Let us apply this method to the homonuclear diatomic hydrogen molecule. Consider the hydrogen molecule consisting of two atoms A and B. Each hydrogen atom in the ground state has one electron in $1 \mathrm{~s}$ orbital. The atomic orbitals of these atoms may be represented by the wave functions $\psi_{\mathrm{A}}$ and $\psi_{\mathrm{B}}$. Mathematically, the formation of molecular orbitals may be described by the linear combination of atomic orbitals that can take place by addition and by subtraction of wave functions of individual atomic orbitals as shown below :
$$ \psi_{\mathrm{MO}}=\psi_{\mathrm{A}} \pm \psi_{\mathrm{B}} $$
Therefore, the two molecular orbitals $\sigma$ and $\sigma^{*}$ are formed as :
$$ \begin{aligned} & \sigma=\psi_{\mathrm{A}}+\psi_{\mathrm{B}} \\ & \sigma^{*}=\psi_{\mathrm{A}}-\psi_{\mathrm{B}} \end{aligned} $$
The molecular orbital $\sigma$ formed by the addition of atomic orbitals is called the bonding molecular orbital while the molecular orbital $\sigma^{*}$ formed by the subtraction of atomic orbital is called antibonding molecular orbital as depicted in Fig. 4.19.
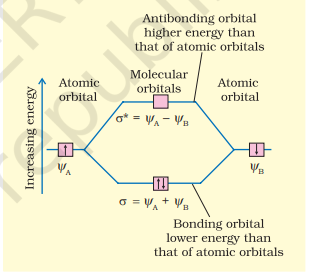
Fig.4.19 Formation of bonding (σ) and antibonding (σ*) molecular orbitals by the linear combination of atomic orbitals ψA and ψB centered on two atoms A and B respectively.
Qualitatively, the formation of molecular orbitals can be understood in terms of the constructive or destructive interference of the electron waves of the combining atoms. In the formation of bonding molecular orbital, the two electron waves of the bonding atoms reinforce each other due to constructive interference while in the formation of antibonding molecular orbital, the electron waves cancel each other due to destructive interference. As a result, the electron density in a bonding molecular orbital is located between the nuclei of the bonded atoms because of which the repulsion between the nuclei is very less while in case of an antibonding molecular orbital, most of the electron density is located away from the space between the nuclei. Infact, there is a nodal plane (on which the electron density is zero) between the nuclei and hence the repulsion between the nuclei is high. Electrons placed in a bonding molecular orbital tend to hold the nuclei together and stabilise a molecule. Therefore, a bonding molecular orbital always possesses lower energy than either of the atomic orbitals that have combined to form it. In contrast, the electrons placed in the antibonding molecular orbital destabilise the molecule. This is because the mutual repulsion of the electrons in this orbital is more than the attraction between the electrons and the nuclei, which causes a net increase in energy.
It may be noted that the energy of the antibonding orbital is raised above the energy of the parent atomic orbitals that have combined and the energy of the bonding orbital has been lowered than the parent orbitals. The total energy of two molecular orbitals, however, remains the same as that of two original atomic orbitals.
4.7.2 Conditions for the Combination of Atomic Orbitals
The linear combination of atomic orbitals to form molecular orbitals takes place only if the following conditions are satisfied:
1. The combining atomic orbitals must have the same or nearly the same energy. This means that $1 \mathrm{~s}$ orbital can combine with another $1 s$ orbital but not with $2 s$ orbital because the energy of $2 s$ orbital is appreciably higher than that of $1 \mathrm{~s}$ orbital. This is not true if the atoms are very different.
2. The combining atomic orbitals must have the same symmetry about the molecular axis. By convention $z$-axis is taken as the molecular axis. It is important to note that atomic orbitals having same or nearly the same energy will not combine if they do not have the same symmetry. For example, $2 p_{z}$ orbital of one atom can combine with $2 p_{z}$ orbital of the other atom but not with the $2 p_{x}$ or $2 p_{y}$ orbitals because of their different symmetries.
3. The combining atomic orbitals must overlap to the maximum extent. Greater the extent of overlap, the greater will be the electron-density between the nuclei of a molecular orbital.
4.7.3 Types of Molecular Orbitals
Molecular orbitals of diatomic molecules are designated as $\sigma$ (sigma), $\pi$ (pi), $\delta$ (delta), etc. In this nomenclature, the sigma $(\sigma)$ molecular orbitals are symmetrical around the bond-axis while pi $(\pi)$ molecular orbitals are not symmetrical. For example, the linear combination of $1 \mathrm{~s}$ orbitals centered on two nuclei produces two molecular orbitals which are symmetrical around the bond-axis. Such molecular orbitals are of the $\sigma$ type and are designated as $\sigma 1 \mathrm{~s}$ and $\sigma^* 1 \mathrm{~s}$ [Fig. 4.20(a), page 124]. If internuclear axis is taken to be in the $\mathrm{z}$ -direction, it can be seen that a linear combination of $2 p_z$ - orbitals of two atoms also produces two sigma molecular orbitals designated as $\boldsymbol{\sigma} \boldsymbol{p}_z$ and $\sigma^{\boldsymbol{*}} \boldsymbol{2}_z$. [Fig. 4.20(b)]
Molecular orbitals obtained from $2 p_{\mathrm{x}}$ and $2 p$ orbitals are not symmetrical around the bond axis because of the presence of positive lobes above and negative lobes below the molecular plane. Such molecular orbitals, are labelled as $\pi$ and $=\pi^{*}$ [Fig. 4.20(c)]. A $\pi$ bonding MO has larger electron density above and below the inter-nuclear axis. The $\pi^{\star}$ antibonding MO has a node between the nuclei.
4.7.4 Energy Level Diagram for Molecular Orbitals
We have seen that $1 \mathrm{~s}$ atomic orbitals on two atoms form two molecular orbitals designated as $\sigma 1 \mathrm{~s}$ and $\sigma^{*} 1 \mathrm{~s}$. In the same manner, the $2 \mathrm{~s}$ and $2 p$ atomic orbitals (eight atomic orbitals on two atoms) give rise to the following eight molecular orbitals:
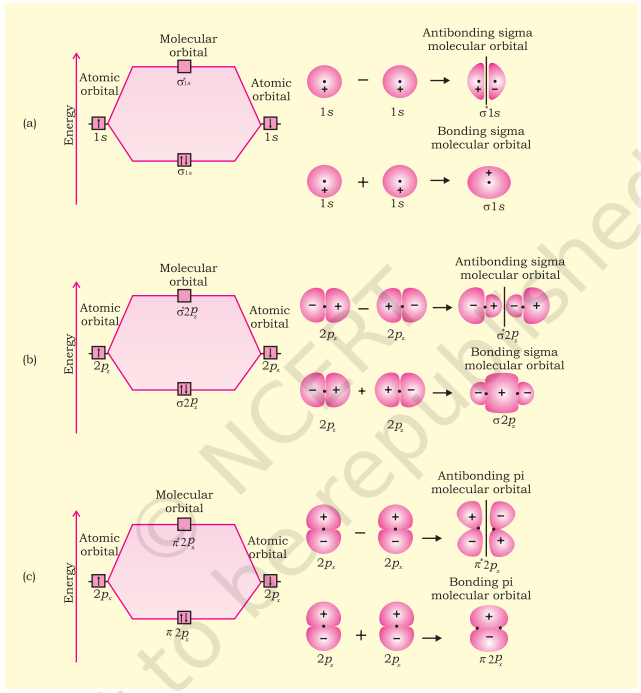
Fig. 4.20 Contours and energies of bonding and antibonding molecular orbitals formed through combinations of (a) 1s atomic orbitals; (b) $2p_z$ atomic orbitals and (c) $2p_x$ atomic orbitals.
$\begin{array}{llllll} \text{Antibonding } & \mathrm{MOs} & \sigma^* 2 s & \sigma^* 2 p_z & \pi^* 2 p_x & \pi^* 2 p_y \\ \text { Bonding } & \mathrm{MOs} & \sigma 2 \mathrm{~s} & \sigma 2 p_{z} & \pi 2 p_{x} & \pi 2 p_{y}\end{array}$
The energy levels of these molecular orbitals have been determined experimentally from spectroscopic data for homonuclear diatomic molecules of second row elements of the periodic table. The increasing order of energies of various molecular orbitals for $\mathrm{O}_2$ and $\mathrm{F}_2$ is given below:
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\sigma 2 p_z < \left(\pi 2 p_x = \pi 2 p_y\right) $
$<\left(\pi^* 2 p_x=\pi^* 2 p_y\right) < \sigma^* 2 p_z$
However, this sequence of energy levels of molecular orbitals is not correct for the remaining molecules $\mathrm{Li}_2, \mathrm{Be}_2, \mathrm{~B}_2, \mathrm{C}_2, \mathrm{~N}_2$. For instance, it has been observed experimentally that for molecules such as $\mathrm{B}_2, \mathrm{C}_2, \mathrm{~N}_2$, etc. the increasing order of energies of various molecular orbitals is
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)$
$<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z$
The important characteristic feature of this order is that the energy of $\boldsymbol{\sigma 2} \boldsymbol{p}_z$ molecular orbital is higher than that of $\pi 2 p_x$ and $\pi 2 p_y$ molecular orbitals.
4.7.5 Electronic Configuration and Molecular Behaviour
The distribution of electrons among various molecular orbitals is called the electronic configuration of the molecule. From the electronic configuration of the molecule, it is possible to get important information about the molecule as discussed below.
Stability of Molecules: If $\mathrm{N}_b$ is the number of electrons occupying bonding orbitals and $\mathrm{N}_a$ the number occupying the antibonding orbitals, then
(i) the molecule is stable if $\mathrm{N}_b$ is greater than $\mathrm{N}_a$, and
(ii) the molecule is unstable if $\mathrm{N}_b$ is less than $\mathrm{N}_a$.
In (i) more bonding orbitals are occupied and so the bonding influence is stronger and a stable molecule results. In (ii) the antibonding influence is stronger and therefore the molecule is unstable.
Bond order
Bond order (b.o.) is defined as one half the difference between the number of electrons present in the bonding and the antibonding orbitals i.e.,
Bond order (b.o.) $=1 / 2\left(\mathrm{~N}_b-\mathrm{N}_a\right)$
The rules discussed above regarding the stability of the molecule can be restated in terms of bond order as follows: A positive bond order (i.e., $\mathrm{N}_b>\mathrm{N}_a$ ) means a stable molecule while a negative (i.e., $\mathrm{N}_b < \mathrm{N}_a$ ) or zero (i.e., $\mathrm{N}_b=\mathrm{N}_a$ ) bond order means an unstable molecule.
Nature of the bond
Integral bond order values of 1,2 or 3 correspond to single, double or triple bonds respectively as studied in the classical concept.
Bond-length
The bond order between two atoms in a molecule may be taken as an approximate measure of the bond length. The bond length decreases as bond order increases.
Magnetic nature
If all the molecular orbitals in a molecule are doubly occupied, the substance is diamagnetic (repelled by magnetic field). However if one or more molecular orbitals are singly occupied it is paramagnetic (attracted by magnetic field), e.g., $\mathrm{O}_{2}$ molecule.
4.8 BONDING IN SOME HOMONUCLEAR DIATOMIC MOLECULES
In this section we shall discuss bonding in some homonuclear diatomic molecules.
1. Hydrogen molecule $\left(\boldsymbol{H}_{2}\right)$ : It is formed by the combination of two hydrogen atoms. Each hydrogen atom has one electron in 1 s orbital. Therefore, in all there are two electrons in hydrogen molecule which are present in $\sigma 1 \mathrm{~s}$ molecular orbital. So electronic configuration of hydrogen molecule is
$$ \mathrm{H}_{2}:(\sigma 1 s)^{2} $$
The bond order of $\mathrm{H}_{2}$ molecule can be calculated as given below:
$$ \text { Bond order }=\frac{\mathrm{N}_b-\mathrm{N}_a}{2}=\frac{2-0}{2}=1 $$
This means that the two hydrogen atoms are bonded together by a single covalent bond. The bond dissociation energy of hydrogen molecule has been found to be $438 \mathrm{~kJ} \mathrm{~mol}^{-1}$ and bond length equal to $74 \mathrm{pm}$. Since no unpaired electron is present in hydrogen molecule, therefore, it is diamagnetic.
2. Helium molecule $\left(\mathbf{H e}_2\right)$ : The electronic configuration of helium atom is $1 s^2$. Each helium atom contains 2 electrons, therefore, in $\mathrm{He}_2$ molecule there would be 4 electrons. These electrons will be accommodated in $\sigma 1 s$ and $\sigma^{*} 1 s$ molecular orbitals leading to electronic configuration:
$\mathrm{He}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$
Bond order of $\mathrm{He}_{2}$ is $1 / 2(2-2)=0$
$\mathrm{He}_{2}$ molecule is therefore unstable and does not exist.
Similarly, it can be shown that $\mathrm{Be}_2$ molecule $(\sigma 1 s)^2\left(\sigma^* 1 s\right)^2(\sigma 2 s)^2\left(\sigma^* 2 s\right)^2$ also does not exist.
3. Lithium molecule $\left(\mathbf{L i}_2\right)$ : The electronic configuration of lithium is $1 s^2, 2 s^1$. There are six electrons in $\mathrm{Li}_2$. The electronic configuration of $\mathrm{Li}_2$ molecule, therefore, is
$$ \operatorname{Li}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2} $$
The above configuration is also written as $\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}$ where $\mathrm{KK}$ represents the closed $K$ shell structure $(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}$.
From the electronic configuration of $\mathrm{Li}_2$ molecule it is clear that there are four electrons present in bonding molecular orbitals and two electrons present in antibonding molecular orbitals. Its bond order, therefore, is $1 / 2$ (42) $=1$. It means that $\mathrm{Li}_2$ molecule is stable and since it has no unpaired electrons it should be diamagnetic. Indeed diamagnetic $\mathrm{Li}_2$ molecules are known to exist in the vapour phase.
4. Carbon molecule $\left(\boldsymbol{C}_2\right)$ : The electronic configuration of carbon is $1 s^{2} 2 s^{2} 2 p^{2}$. There are twelve electrons in $\mathrm{C}_2$. The electronic configuration of $\mathrm{C}_2$ molecule, therefore, is
$\mathrm{C}_2:(\sigma 1 \mathrm{~s})^{2}\left(\sigma^{*} 1 \mathrm{~s}\right)^{2}(\sigma * 2 \mathrm{~s})^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
or $K K(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
The bond order of $\mathrm{C}_2$ is $1 / 2(8-4)=2$ and $\mathrm{C}_2$ should be diamagnetic. Diamagnetic $\mathrm{C}_2$ molecules have indeed been detected in vapour phase. It is important to note that double bond in $\mathrm{C}_2$ consists of both pi bonds because of the presence of four electrons in two pi molecular orbitals. In most of the other molecules a double bond is made up of a sigma bond and a pi bond. In a similar fashion the bonding in $\mathrm{N}_2$ molecule can be discussed.
5. Oxygen molecule $\left(\mathrm{O}_2\right)$ : The electronic configuration of oxygen atom is $1 s^{2} 2 s^{2} 2 p^{4}$. Each oxygen atom has 8 electrons, hence, in $\mathrm{O}_2$ molecule there are 16 electrons. The electronic configuration of $\mathrm{O}_2$ molecule, therefore, is
$\mathrm{O}_{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\sigma 2 \mathrm{p}_z\right)^{2}$
$\left(\pi 2 p_x{ }^{2} \equiv \pi 2 p_y{ }^{2}\right)\left(\pi^{*} 2 p^{1}{ }_x \equiv \pi * 2 p_y{ }^{1}\right)$
or $\mathrm{O}^{2}:\left[\begin{array}{c}\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}\left(\sigma 2 p_S\right)^{2}\left(\sigma 2 p_z\right)^{2} \\ \left(\pi 2 p_x^{2} \equiv \pi 2 p_y^{2}\right),\left(\pi * 2 \mathrm{p}_x^{1} \equiv \pi * 2_y^{1}\right)\end{array}\right]$
From the electronic configuration of $\mathrm{O}_{2}$ molecule it is clear that ten electrons are present in bonding molecular orbitals and six electrons are present in antibonding molecular orbitals. Its bond order, therefore, is
Bond order $=\frac{1}{2}\left[N_{b}-N_{a}\right]=\frac{1}{2}[10-6]=2$
So in oxygen molecule, atoms are held by a double bond. Moreover, it may be noted that it contains two unpaired electrons in $\pi^* 2 p_x$ and $\pi^* 2 p_y$ molecular orbitals, therefore, $\mathrm{O}_2$ molecule should be paramagnetic, a prediction that corresponds to experimental observation. In this way, the theory successfully explains the paramagnetic nature of oxygen.
Similarly, the electronic configurations of other homonuclear diatomic molecules of the second row of the periodic table can be written. In Fig. 4.21 are given the molecular orbital occupancy and molecular properties for $\mathrm{B}_2$ through $\mathrm{Ne}_2$. The sequence of MOs and their electron population are shown. The bond energy, bond length, bond order, magnetic properties and valence electron configuration appear below the orbital diagrams.
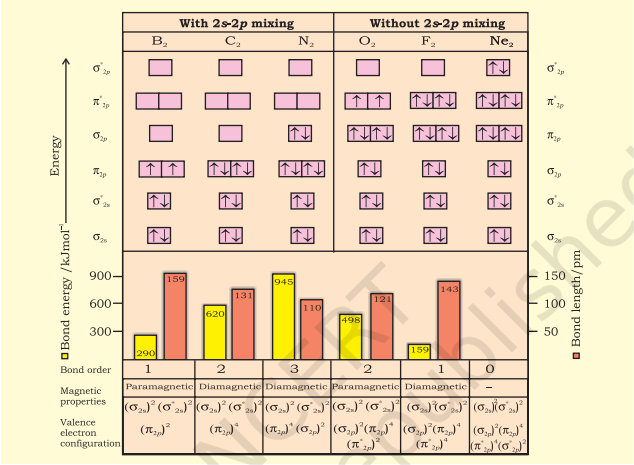
Fig.4.21 MO occupancy and molecular properties for $B_2$ through $Ne_2$.
4.9 HYDROGEN BONDING
Nitrogen, oxygen and fluorine are the highly electronegative elements. When they are attached to a hydrogen atom to form covalent bond, the electrons of the covalent bond are shifted towards the more electronegative atom. This partially positively charged hydrogen atom forms a bond with the other more electronegative atom. This bond is known as hydrogen bond and is weaker than the covalent bond. For example, in HF molecule, the hydrogen bond exists between hydrogen atom of one molecule and fluorine atom of another molecule as depicted below :
$\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}$
Here, hydrogen bond acts as a bridge between two atoms which holds one atom by covalent bond and the other by hydrogen bond. Hydrogen bond is represented by a dotted line ($\text{ - - - }$) while a solid line represents the covalent bond. Thus, hydrogen bond can be defined as the attractive force which binds hydrogen atom of one molecule with the electronegative atom ( $\mathrm{F}, \mathrm{O}$ or $\mathrm{N}$ ) of another molecule.
4.9.1 Cause of Formation of Hydrogen Bond
When hydrogen is bonded to strongly electronegative element ’ $\mathrm{X}$ ‘, the electron pair shared between the two atoms moves far away from hydrogen atom. As a result the hydrogen atom becomes highly electropositive with respect to the other atom ’ $X$ ‘. Since there is displacement of electrons towards $\mathrm{X}$, the hydrogen acquires fractional positive charge $\left(\delta^{+}\right)$while ’ $\mathrm{X}$ ’ attain fractional negative charge $\left(\delta^{-}\right)$. This results in the formation of a polar molecule having electrostatic force of attraction which can be represented as:
$\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}$
The magnitude of $\mathrm{H}$-bonding depends on the physical state of the compound. It is maximum in the solid state and minimum in the gaseous state. Thus, the hydrogen bonds have strong influence on the structure and properties of the compounds.
4.9.2 Types of $H$-Bonds
There are two types of $\mathrm{H}$-bonds
(i) Intermolecular hydrogen bond
(ii) Intramolecular hydrogen bond
(1) Intermolecular hydrogen bond: It is formed between two different molecules of the same or different compounds. For example, $\mathrm{H}$-bond in case of HF molecule, alcohol or water molecules, etc.
(2) Intramolecular hydrogen bond : It is formed when hydrogen atom is in between the two highly electronegative $(\mathrm{F}, \mathrm{O}, \mathrm{N})$ atoms present within the same molecule. For example, in o-nitrophenol the hydrogen is in between the two oxygen atoms.
Fig. 4.22 Intramolecular hydrogen
Summary
Kössel’s first insight into the mechanism of formation of electropositive and electronegative ions related the process to the attainment of noble gas configurations by the respective ions. Electrostatic attraction between ions is the cause for their stability. This gives the concept of electrovalency.
The first description of covalent bonding was provided by Lewis in terms of the sharing of electron pairs between atoms and he related the process to the attainment of noble gas configurations by reacting atoms as a result of sharing of electrons. The Lewis dot symbols show the number of valence electrons of the atoms of a given element and Lewis dot structures show pictorial representations of bonding in molecules.
An ionic compound is pictured as a three-dimensional aggregation of positive and negative ions in an ordered arrangement called the crystal lattice. In a crystalline solid there is a charge balance between the positive and negative ions. The crystal lattice is stabilized by the enthalpy of lattice formation.
While a single covalent bond is formed by sharing of an electron pair between two atoms, multiple bonds result from the sharing of two or three electron pairs. Some bonded atoms have additional pairs of electrons not involved in bonding. These are called lone-pairs of electrons. A Lewis dot structure shows the arrangement of bonded pairs and lone pairs around each atom in a molecule. Important parameters, associated with chemical bonds, like: bond length, bond angle, bond enthalpy, bond order and bond polarity have significant effect on the properties of compounds.
A number of molecules and polyatomic ions cannot be described accurately by a single Lewis structure and a number of descriptions (representations) based on the same skeletal structure are written and these taken together represent the molecule or ion. This is a very important and extremely useful concept called resonance. The contributing structures or canonical forms taken together constitute the resonance hybrid which represents the molecule or ion.
The VSEPR model used for predicting the geometrical shapes of molecules is based on the assumption that electron pairs repel each other and, therefore, tend to remain as far apart as possible. According to this model, molecular geometry is determined by repulsions between lone pairs and lone pairs; lone pairs and bonding pairs and bonding pairs and bonding pairs. The order of these repulsions being : lp-lp $>1 \mathrm{p}-\mathrm{bp}>\mathrm{bp}-\mathrm{bp}$
The valence bond (VB) approach to covalent bonding is basically concerned with the energetics of covalent bond formation about which the Lewis and VSEPR models are silent. Basically the VB theory discusses bond formation in terms of overlap of orbitals. For example the formation of the $\mathrm{H}_{2}$ molecule from two hydrogen atoms involves the overlap of the $1 \mathrm{~s}$ orbitals of the two $\mathrm{H}$ atoms which are singly occupied. It is seen that the potential energy of the system gets lowered as the two $\mathrm{H}$ atoms come near to each other. At the equilibrium inter-nuclear distance (bond distance) the energy touches a minimum. Any attempt to bring the nuclei still closer results in a sudden increase in energy and consequent destabilization of the molecule. Because of orbital overlap the electron density between the nuclei increases which helps in bringing them closer. It is however seen that the actual bond enthalpy and bond length values are not obtained by overlap alone and other variables have to be taken into account.
For explaining the characteristic shapes of polyatomic molecules Pauling introduced the concept of hybridisation of atomic orbitals. $s p, s p^{2}, s p^{3}$ hybridizations of atomic orbitals of $\mathrm{Be}, \mathrm{B}, \mathrm{C}, \mathrm{N}$ and $\mathrm{O}$ are used to explain the formation and geometrical shapes of molecules like $\mathrm{BeCl}_2, \mathrm{BCl}_3, \mathrm{CH}_4, \mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$. They also explain the formation of multiple bonds in molecules like $\mathrm{C}_2 \mathrm{H}_2$ and $\mathrm{C}_2 \mathrm{H}_4$.
The molecular orbital (MO) theory describes bonding in terms of the combination and arrangment of atomic orbitals to form molecular orbitals that are associated with the molecule as a whole. The number of molecular orbitals are always equal to the number of atomic orbitals from which they are formed. Bonding molecular orbitals increase electron density between the nuclei and are lower in energy than the individual atomic orbitals. Antibonding molecular orbitals have a region of zero electron density between the nuclei and have more energy than the individual atomic orbitals.
The electronic configuration of the molecules is written by filling electrons in the molecular orbitals in the order of increasing energy levels. As in the case of atoms, the Pauli exclusion principle and Hund’s rule are applicable for the filling of molecular orbitals. Molecules are said to be stable if the number of elctrons in bonding molecular orbitals is greater than that in antibonding molecular orbitals.
Hydrogen bond is formed when a hydrogen atom finds itself between two highly electronegative atoms such as F, O and N. It may be intermolecular (existing between two or more molecules of the same or different substances) or intramolecular (present within the same molecule). Hydrogen bonds have a powerful effect on the structure and properties of many compounds.
Exercise
4.1 Explain the formation of a chemical bond.
Show Answer
Answer A chemical bond is defined as an attractive force that holds the constituents (atoms, ions etc.) together in a chemical species.
Various theories have been suggested for the formation of chemical bonds such as the electronic theory, valence shell electron pair repulsion theory, valence bond theory, and molecular orbital theory.
A chemical bond formation is attributed to the tendency of a system to attain stability. It was observed that the inertness of noble gases was because of their fully filled outermost orbitals. Hence, it was postulated that the elements having incomplete outermost shells are unstable (reactive). Atoms, therefore, combine with each other and complete their respective octets or duplets to attain the stable configuration of the nearest noble gases. This combination can occur either by sharing of electrons or by transferring one or more electrons from one atom to another. The chemical bond formed as a result of sharing of electrons between atoms is called a covalent bond. An ionic bond is formed as a result of the transference of electrons from one atom to another.
4.2 Write Lewis dot symbols for atoms of the following elements : Mg, Na, B, O, N, Br.
Show Answer
Answer
Mg: There are two valence electrons in Mg atom. Hence, the Lewis dot symbol for Mg is: $\ddot{M} g$
Na: There is only one valence electron in an atom of sodium. Hence, the Lewis dot structure is: Na*
B: There are 3 valence electrons in Boron atom. Hence, the Lewis dot structure is: ${ }^{B} \cdot$
O.: There are six valence electrons in an atom of oxygen. Hence, the Lewis dot structure is: $: \ddot{0}$ :
$\underline{N}$ : There are five valence electrons in an atom of nitrogen. Hence, the Lewis dot structure is: $: \ddot{N}^{*}$
Br: There are seven valence electrons in bromine. Hence, the Lewis dot structure is: $: \ddot{Br}$ :
4.3 Write Lewis symbols for the following atoms and ions: $\mathrm{S}$ and $\mathrm{S}^{2-} ; \mathrm{Al}$ and $\mathrm{Al}^{3+} ; \mathrm{H}$ and $\mathrm{H}^{-}$
Show Answer
Answer
(i) $S$ and $S^{2}$
The number of valence electrons in sulphur is 6 .
The Lewis dot symbol of sulphur ( $S$ ) is $: \ddot{s}$ :
The dinegative charge infers that there will be two electrons more in addition to the six valence electrons. Hence, the Lewis dot symbol of $S^{2 \cdot}$ is
(ii) $Al$ and $Al^{3+}$
The number of valence electrons in aluminium is 3 .
The Lewis dot symbol of aluminium (Al) is $\ddot{Al}$.
The tripositive charge on a species infers that it has donated its three electrons. Hence, the Lewis dot symbol is $[Al]^{3+}$.
(iii) $H$ and $H$
The number of valence electrons in hydrogen is 1.
The Lewis dot symbol of hydrogen $(H)$ is $H$ :
The uninegative charge infers that there will be one electron more in addition to the one valence electron. Hence, the Lewis dot symbol is $[\ddot{H}]^{-}$.
4.4 Draw the Lewis structures for the following molecules and ions :
$\mathrm{H}_2 \mathrm{~S}, \mathrm{SiCl}_4, \mathrm{BeF}_2, \mathrm{CO}_3^{2-}$, $\mathrm{HCOOH}$
Show Answer
Answer $H_2 S$
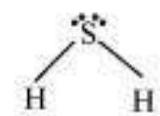
$SiCl_4$
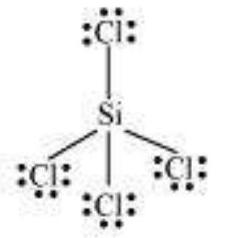
$BeF_2$
$ \ddot{:} F-Be-\ddot{F} $
$CO_3^{2-}$
4.5 Define octet rule. Write its significance and limitations.
Show Answer
Answer
The octet rule or the electronic theory of chemical bonding was developed by Kossel and Lewis. According to this rule, atoms can combine either by transfer of valence electrons from one atom to another or by sharing their valence electrons in order to attain the nearest noble gas configuration by having an octet in their valence shell.
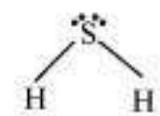
The octet rule successfully explained the formation of chemical bonds depending upon the nature of the element.
Limitations of the octet theory:
The following are the limitations of the octet rule:
(a) The rule failed to predict the shape and relative stability of molecules.
(b) It is based upon the inert nature of noble gases. However, some noble gases like xenon and krypton form compounds such as $XeF_2, KrF_2$ etc.
(c) The octet rule cannot be applied to the elements in and beyond the third period of the periodic table. The elements present in these periods have more than eight valence electrons around the central atom. For example: $PF_5, SF_6$, etc.
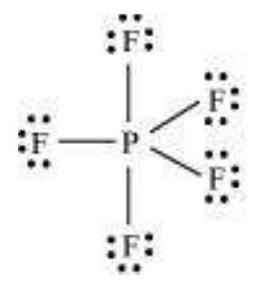
(d) The octet rule is not satisfied for all atoms in a molecule having an odd number of electrons. For example, NO and $NO_2$ do not satisfy the octet rule.
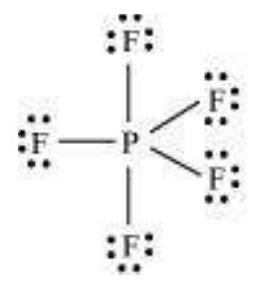
(e) This rule cannot be applied to those compounds in which the number of electrons surrounding the central atom is less than eight. For example, $LiCl, BeH_2, AlCl_3$ etc. do not obey the octet rule. $Li: Cl$ $Cl: . Al: Cl$ ci $H: Be: H$
4.6 Write the favourable factors for the formation of ionic bond.
Show Answer
Answer
An ionic bond is formed by the transfer of one or more electrons from one atom to another. Hence, the formation of ionic bonds depends upon the ease with which neutral atoms can lose or gain electrons. Bond formation also depends upon the lattice energy of the compound formed.
Hence, favourable factors for ionic bond formation are as follows:
(i) Low ionization enthalpy of metal atom.
(ii) High electron gain enthalpy $(\Delta _{e g} H)$ of a non-metal atom.
(iii) High lattice energy of the compound formed.
4.7 Discuss the shape of the following molecules using the VSEPR model:
$\mathrm{BeCl}_2, \mathrm{BCl}_3, \mathrm{SiCl}_4, \mathrm{AsF}_5, \mathrm{H}_2 \mathrm{~S}, \mathrm{PH}_3$
Show Answer
Answer
$\underline{BeCl_2}$
$Cl: Be: Cl$
The central atom has no lone pair and there are two bond pairs. i.e., $BeCl_2$ is of the type $AB_2$. Hence, it has a linear shape.
$BCl_3$
$\stackrel{Cl}{: B}: Cl$
The central atom has no lone pair and there are three bond pairs. Hence, it is of the type $AB_3$. Hence, it is trigonal planar.
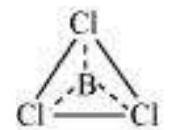
$\underline{SiCl_4}$
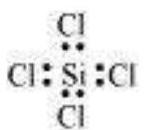
The central atom has no lone pair and there are four bond pairs. Hence, the shape of $SiCl_4$ is tetrahedral being the $AB_4$ type molecule.
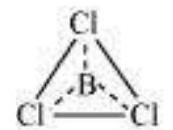
The central atom has no lone pair and there are five bond pairs. Hence, $AsF_5$ is of the type $AB_5$. Therefore, the shape istrigonal bipyramidal.
$H_2 S$ :
н: $\ddot{s}: H$
The central atom has one lone pair and there are two bond pairs. Hence, $H_2 S$ is of the type $AB_2 E$. The shape is Bent.
$PH_3:$
$H: \underset{H}{\ddot{P}}: H$
The central atom has one lone pair and there are three bond pairs. Hence, $PH_3$ is of the $AB_3 E$ type. Therefore, the shape is trigonal pyramidal.
4.8 Although geometries of $\mathrm{NH}_3$ and $\mathrm{H}_2 \mathrm{O}$ molecules are distorted tetrahedral, bond angle in water is less than that of ammonia. Discuss.
Show Answer
Answer
The molecular geometry of $NH_3$ and $H_2 O$ can be shown as:

The central atom $(N)$ in $NH_3$ has one lone pair and there are three bond pairs. In $H_2 O$, there are two lone pairs and two bond pairs.
The two lone pairs present in the oxygen atom of $H_2 O$ molecule repels the two bond pairs. This repulsion is stronger than the repulsion between the lone pair and the three bond pairs on the nitrogen atom.
Since the repulsions on the bond pairs in $H_2 O$ molecule are greater than that in $NH_3$, the bond angle in water is less than that of ammonia.
4.9 How do you express the bond strength in terms of bond order ?
Show Answer
Answer
Bond strength represents the extent of bonding between two atoms forming a molecule. The larger the bond energy, the stronger is the bond and the greater is the bond order.
4.10 Define the bond length.
Show Answer
Answer
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule.
Bond lengths are expressed in terms of Angstrom $(10^{-10} m)$ or picometer
$(10^{-12} m)$ and are measured by spectroscopic X-ray diffractions and electron-diffraction techniques.
In an ionic compound, the bond length is the sum of the ionic radii of the constituting atoms $(d=r _{+}+r _{\text{. }}.$. In a covalent compound, it is the sum of their covalent radii $(d=r_A+r_B)$.

4.11 Explain the important aspects of resonance with reference to the $\mathrm{CO}_{3}^{2-}$ ion.
Show Answer
Answer
According to experimental findings, all carbon to oxygen bonds in $CO_3^{2-}$ are equivalent. Hence, it is inadequate to represent $CO_3^{2-}$ ion by a single Lewis structure having two single bonds and one double bond.
Therefore, carbonate ion is described as a resonance hybrid of the following structures:
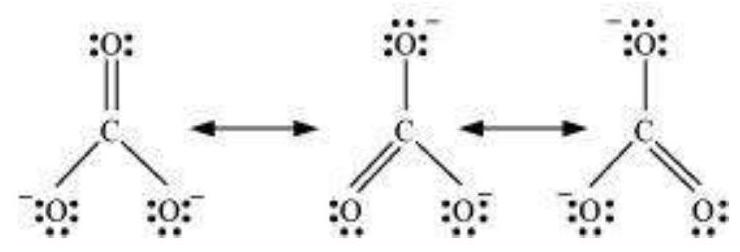
4.12 $ \mathrm{H}_3 \mathrm{PO}_3$ can be represented by structures 1 and 2 shown below. Can these two structures be taken as the canonical forms of the resonance hybrid representing $\mathrm{H}_3 \mathrm{PO}_3$ ? If not, give reasons for the same.

Show Answer
Answer
The given structures cannot be taken as the canonical forms of the resonance hybrid of $H_3 PO_3$ because the positions of the atoms have changed.
4.13 Write the resonance structures for $\mathrm{SO}_3, \mathrm{NO}_2$ and $\mathrm{NO}_3^{-}$.
Show Answer
Answer
The resonance structures are:
(a) $SO_3$ :
(b) $NO_2$ :
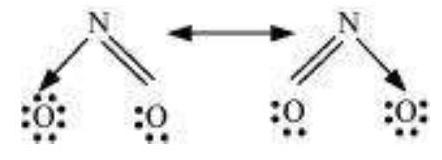
(c) $NO_3^{-}$:
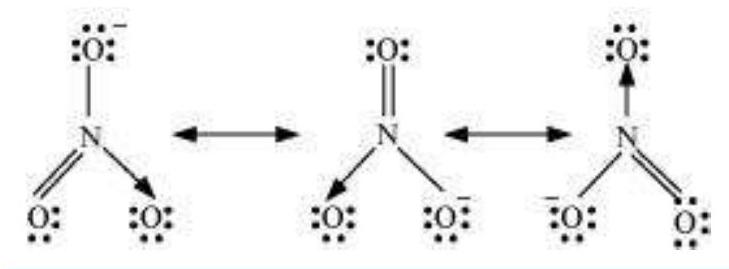
4.14 Use Lewis symbols to show electron transfer between the following atoms to form cations and anions : (a) $\mathrm{K}$ and $\mathrm{S}$ (b) $\mathrm{Ca}$ and $\mathrm{O}$ (c) $\mathrm{Al}$ and $\mathrm{N}$.
Show Answer
Answer
(a) $K$ and $S$ :
The electronic configurations of $K$ and $S$ are as follows:
K: 2, 8, 8, 1
S: $2,8,6$
K$\cdot$
$ \text{ : } $
Sulphur (S) requires 2 more electrons to complete its octet. Potassium (K) requires one electron more than the nearest noble gas i.e., Argon. Hence, the electron transfer can be shown as:
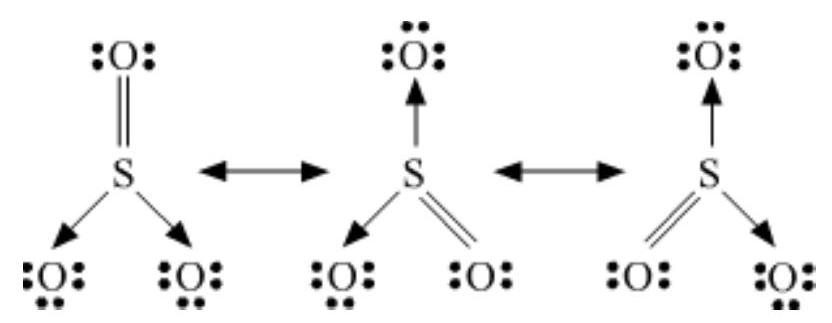
(b) Ca and O:
The electronic configurations of $Ca$ and $O$ are as follows:
Ca: $2,8,8,2$
O: 2,6
Oxygen requires two electrons more to complete its octet, whereas calcium has two electrons more than the nearest noble gas i.e., Argon. Hence, the electron transfer takes place as:

(c) Al and $N$ :
The electronic configurations of $Al$ and $N$ are as follows:
Al: 2, 8, 3
$N: 2,5$
Nitrogen is three electrons short of the nearest noble gas (Neon), whereas aluminium has three electrons more than Neon. Hence, the electron transference can be shown as:

4.15 Although both $\mathrm{CO}_2$ and $\mathrm{H}_2 \mathrm{O}$ are triatomic molecules, the shape of $\mathrm{H}_2 \mathrm{O}$ molecule is bent while that of $\mathrm{CO}_2$ is linear. Explain this on the basis of dipole moment.
Show Answer
Answer
According to experimental results, the dipole moment of carbon dioxide is zero. This is possible only if the molecule is linear so that the dipole moments of $C$-O bonds are equal and opposite to nullify each other.
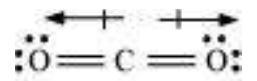
Resultant $\mu=0$ D
$H_2 O$, on the other hand, has a dipole moment value of $1.84 D$ (though it is a triatomic molecule as $CO_2$ ). The value of the dipole moment suggests that the structure of $H_2 O$ molecule is bent where the dipole moment of $O-H$ bonds are unequal.

4.16 Write the significance/applications of dipole moment.
Show Answer
Answer
In heteronuclear molecules, polarization arises due to a difference in the electronegativities of the constituents of atoms. As a result, one end of the molecule acquires a positive charge while the other end becomes negative. Hence, a molecule is said to possess a dipole.
The product of the magnitude of the charge and the distance between the centres of positive-negative charges is called the dipole moment $ \mu $ of the molecule. It is a vector quantity and is represented by an \to with its tail at the positive centre and head pointing towards a negative centre.
Dipole moment $(\mu)=$ charge $(Q) \times$ distance of separation $(r)$
The SI unit of a dipole moment is ’esu'.
1 esu $=3.335 \times 10^{-30} cm$
Dipole moment is the measure of the polarity of a bond. It is used to differentiate between polar and non-polar bonds since all non-polar molecules (e.g. $H_2, O_2$ ) have zero dipole moments. It is also helpful in calculating the percentage ionic character of a molecule.
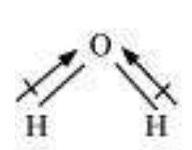
$ \begin{gathered} \stackrel{+}{+}=C=O \\ \mu=0 \end{gathered} $
$ \mu=1.84 D $
4.17 Define electronegativity. How does it differ from electron gain enthalpy?
Show Answer
Answer
Electronegativity is the ability of an atom in a chemical compound to attract a bond pair of electrons towards itself.
Electronegativity of any given element is not constant. It varies according to the element to which it is bound. It is not a measurable quantity. It is only a relative number.
On the other hand, electron gain enthalpy is the enthalpy change that takes place when an electron is added to a neutral gaseous atom to form an anion. It can be negative or positive depending upon whether the electron is added or removed. An element has a constant value of the electron gain enthalpy that can be measured experimentally.
4.18 Explain with the help of suitable example polar covalent bond.
Show Answer
Answer
When two dissimilar atoms having different electronegativities combine to form a covalent bond, the bond pair of electrons is not shared equally. The bond pair shifts towards the nucleus of the atom having greater electronegativity. As a result, electron distribution gets distorted and the electron cloud is displaced towards the electronegative atom.
As a result, the electronegative atom becomes slightly negatively charged while the other atom becomes slightly positively charged. Thus, opposite poles are developed in the molecule and this type of a bond is called a polar covalent bond.
$HCl$, for example, contains a polar covalent bond. Chlorine atom is more electronegative than hydrogen atom. Hence, the bond pair lies towards chlorine and therefore, it acquires a partial negative charge.
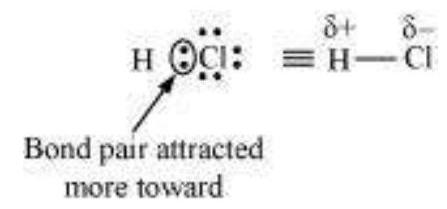
4.19 Arrange the bonds in order of increasing ionic character in the molecules: $\mathrm{LiF}, \mathrm{K}_2 \mathrm{O}$, $\mathrm{N}_2, \mathrm{SO}_2$ and $\mathrm{ClF}_3$.
Show Answer
Answer
The ionic character in a molecule is dependent upon the electronegativity difference between the constituting atoms. The greater the difference, the greater will be the ionic character of the molecule.
On this basis, the order of increasing ionic character in the given molecules is
$N_2<SO_2<ClF_3<K_2 O<LiF$.
4.20 The skeletal structure of $\mathrm{CH}_{3} \mathrm{COOH}$ as shown below is correct, but some of the bonds are shown incorrectly. Write the correct Lewis structure for acetic acid.

Show Answer
Answer
The correct Lewis structure for acetic acid is as follows:
4.21 Apart from tetrahedral geometry, another possible geometry for $\mathrm{CH_4}$ is square planar with the four $\mathrm{H}$ atoms at the corners of the square and the $\mathrm{C}$ atom at its centre. Explain why $\mathrm{CH_4}$ is not square planar?
Show Answer
Answer
Electronic configuration of carbon atom:
$ _6 C: 1 s^{2} 2 s^{2} 2 p^{2}$
In the excited state, the orbital picture of carbon can be represented as:
Hence, carbon atom undergoes $s p^{3}$ hybridization in $CH_4$ molecule and takes a tetrahedral shape.
For a square planar shape, the hybridization of the central atom has to be $d s p^{2}$. However, an atom of carbon does not have $d$-orbitalsto undergo $d s p^{2}$ hybridization. Hence, the structure of $CH_4$ cannot be square planar.
Moreover, with a bond angle of $90^{\circ}$ in square planar, the stability of $CH_4$ will be very less because of the repulsion existing between the bond pairs. Hence, VSEPR theory also supports a tetrahedral structure for $CH_4$.
4.22 Explain why $\mathrm{BeH_2}$ molecule has a zero dipole moment although the $\mathrm{Be}-\mathrm{H}$ bonds are polar.
Show Answer
Answer
The Lewis structure for $BeH_2$ is as follows:
$H: Be: H$
There is no lone pair at the central atom (Be) and there are two bond pairs. Hence, $BeH_2$ is of the type $AB_2$. It has a linear structure.
$H \xrightarrow{\longrightarrow} \xrightarrow{+} H$
Dipole moments of each $H$-Be bond are equal and are in opposite directions. Therefore, they nullify each other. Hence, $BeH_2$ molecule has zero dipole moment.
4.23 Which out of $\mathrm{NH_3}$ and $\mathrm{NF_3}$ has higher dipole moment and why ?
Show Answer
Answer
In both molecules i.e., $NH_3$ and $NF_3$, the central atom $(N)$ has a lone pair electron and there are three bond pairs. Hence, both molecules have a pyramidal shape. Since fluorine is more electronegative than hydrogen, it is expected that the net dipole moment of $NF_3$ is greater than $NH_3$. However, the net dipole moment of $NH_3(1.46 D)$ is greater than that of $NF_3(0.24 D)$.
This can be explained on the basis of the directions of the dipole moments of each individual bond in $NF_3$ and $NH_3$. These directions can be shown as:
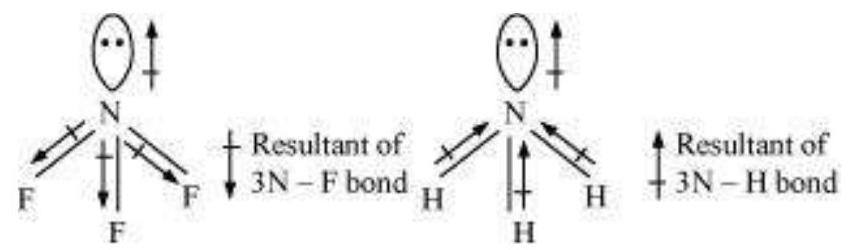
Thus, the resultant moment of the $N-H$ bonds add up to the bond moment of the lone pair (the two being in the same direction), whereas that of the three $N-F$ bonds partly cancels the moment of the lone pair.
Hence, the net dipole moment of $NF_3$ is less than that of $NH_3$.
4.24 What is meant by hybridisation of atomic orbitals? Describe the shapes of $s p, s p^{2}$, $s p^{3}$ hybrid orbitals.
Show Answer
Answer
Hybridization is defined as an intermixing of a set of atomic orbitals of slightly different energies, thereby forming a new set of orbitals having equivalent energies and shapes.
For example, one $2 s$-orbital hybridizes with two $2 p$-orbitals of carbon to form three new $s p^{2}$ hybrid orbitals.
These hybrid orbitals have minimum repulsion between their electron pairs and thus, are more stable. Hybridization helps indicate the geometry of the molecule.
Shape of $s p$ hybrid orbitals: $s p$ hybrid orbitals have a linear shape. They are formed by the intermixing of $s$ and porbitals as:
$s$-orbital
$p_z$-orbital
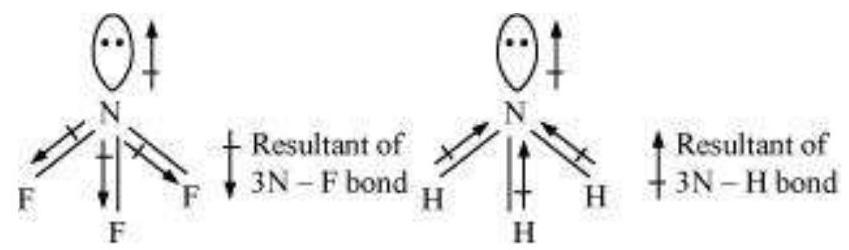
$s p$-hybrids
Shape of $s p^{2}$ hybrid orbitals: $s p^{2}$ hybrid orbitals are formed as a result of the intermixing of one s-orbital and two $2 p$-orbitals. The hybrid orbitals are oriented in a trigonal planar arrangement as:
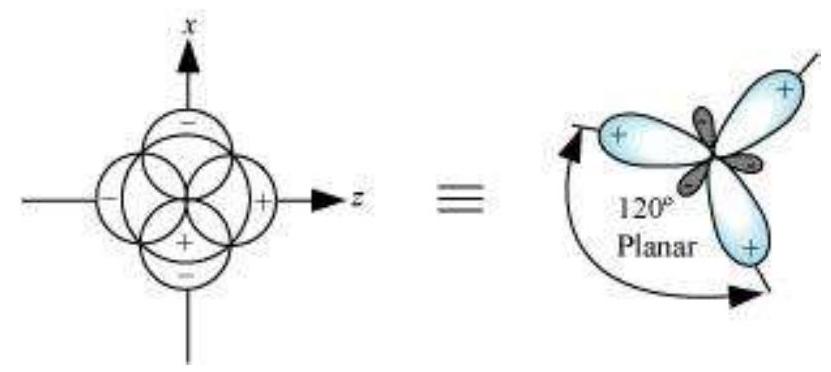
Shape of $s p^{3}$ hybrid orbitals:
Four $s p^{3}$ hybrid orbitals are formed by intermixing one s-orbital with three $p$-orbitals. The four $s p^{3}$ hybrid orbitals are arranged in the form of a tetrahedron as:
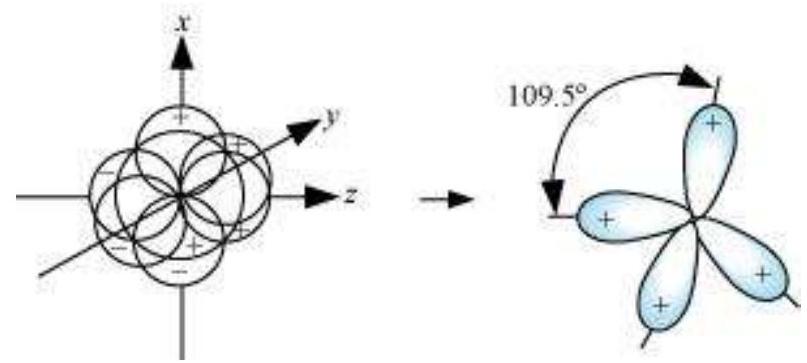
4.25 Describe the change in hybridisation (if any) of the Al atom in the following reaction.
$\mathrm{AlCl_3}+\mathrm{Cl}^{-} \rightarrow \mathrm{AlCl_4}^{-}$
Show Answer
Answer
The valence orbital picture of aluminium in the ground state can be represented as:
$\uparrow$
The orbital picture of aluminium in the excited state can be represented as:
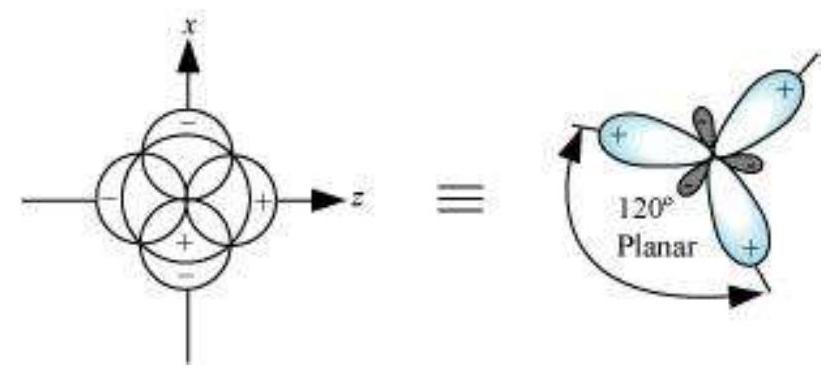
| $\uparrow$ | $\uparrow$ |
|---|
3s $\quad 3 p_x 3 p_y 3 p_z$
Hence, it undergoes $s p^{2}$ hybridization to give a trigonal planar arrangement (in $AlCl_3$ ).
To form $AlCl_4^{-}$, the empty $3 p_z$ orbital also gets involved and the hybridization changes from $s p^{2}$ to $s p^{3}$. As a result, the shape gets changed to tetrahedral.
4.26 Is there any change in the hybridisation of $\mathrm{B}$ and $\mathrm{N}$ atoms as a result of the following reaction?
$\mathrm{BF_3}+\mathrm{NH_3} \rightarrow \mathrm{F_3} \mathrm{~B} \cdot \mathrm{NH_3}$
Show Answer
Answer
Boron atom in $BF_3$ is $s p^{2}$ hybridized. The orbital picture of boron in the excited state can be shown as:
$ \underset{2s}{\boxed{\uparrow}} \quad\quad\quad \underset{2p_x}{\boxed{\uparrow}} \underset{2p_y}{\boxed{\uparrow}}\underset{2p_z}{\Large \boxed{ }}$
Nitrogen atom in $NH_3$ is $s p^{3}$ hybridized. The orbital picture of nitrogen can be represented as:
$ \underset{2s}{\boxed{\uparrow}} \quad\quad\quad \underset{2p_x}{\boxed{\uparrow}} \underset{2p_y}{\boxed{\uparrow}}\underset{2p_z}{\Large \boxed{ }}$
After the reaction has occurred, an adduct $F_3 BA \phi^{\prime \prime}{ }^{\prime \prime}{ }^{\prime} NH_3$ is formed as hybridization of ‘B’ changes to $s p^{3}$. However, the hybridization of ’ $N$ ’ remains intact.
4.27 Draw diagrams showing the formation of a double bond and a triple bond between carbon atoms in $\mathrm{C_2} \mathrm{H_4}$ and $\mathrm{C_2} \mathrm{H_2}$ molecules.
Show Answer
Answer
$C_2 H_4$ :
The electronic configuration of $C$-atom in the excited state is:
$ _6 C=1 s^{2} 2 s^{1} 2 p_x^{1} 2 p_y^{1} 2 p_z^{1}$
In the formation of an ethane molecule $(C_2 H_4)$, one $s p^{2}$ hybrid orbital of carbon overlaps a $s p^{2}$ hybridized orbital of another carbon atom, thereby forming a $C-C$ sigma bond.
The remaining two $s p^{2}$ orbitals of each carbon atom form a $s p^{2}-s$ sigma bond with two hydrogen atoms. The unhybridized orbital of one carbon atom undergoes sidewise overlap with the orbital of a similar kind present on another carbon atom to form a weak $\pi$-bond.
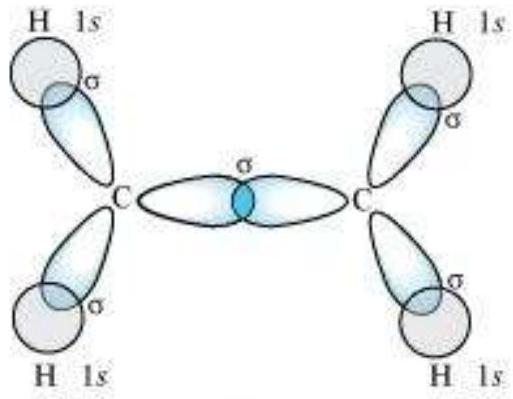
(a)
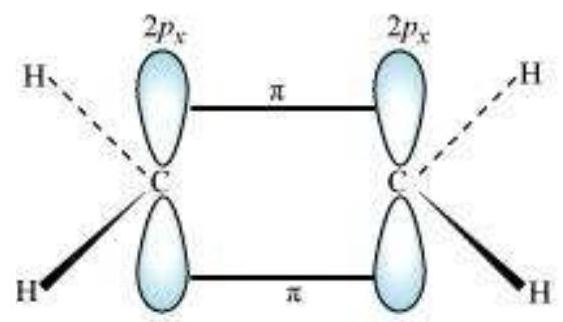
(b)
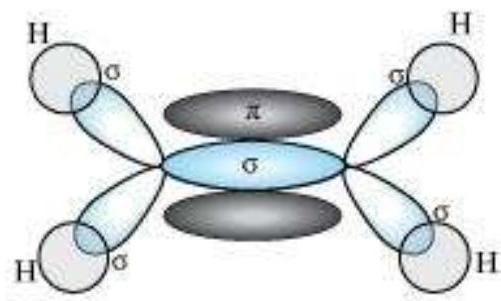
(c)
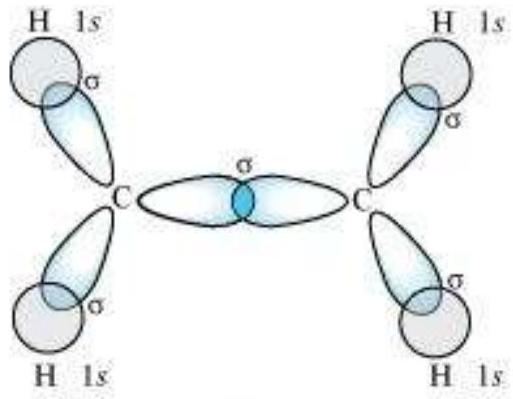
(d)
$\Large C_2 H_2$ :
In the formation of $C_2 H_2$ molecule, each C-atom is $s p$ hybridized with two $2 p$-orbitals in an unhybridized state.
One $s p$ orbital of each carbon atom overlaps with the other along the internuclear axis forming a C- $C$ sigma bond. The second $s p$ orbital of each C-atom overlaps a half-filled $1 s$-orbital to form a $ \sigma $ bond.
The two unhybridized $2 p$-orbitals of the first carbon undergo sidewise overlap with the $2 p$ orbital of another carbon atom, thereby forming two pi ( $\pi$ ) bonds between carbon atoms. Hence, the triple bond between two carbon atoms is made up of one sigma and two $\pi$-bonds.
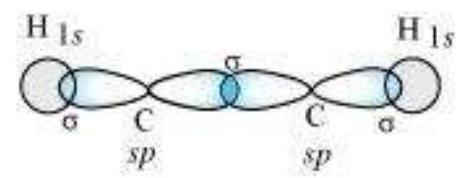
(a)
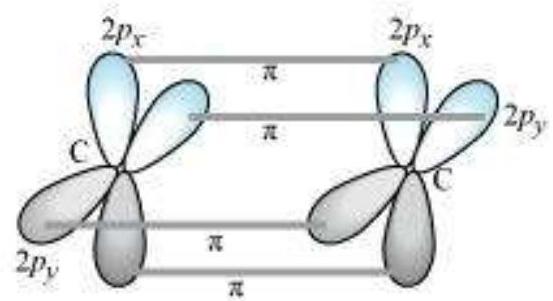
(b)
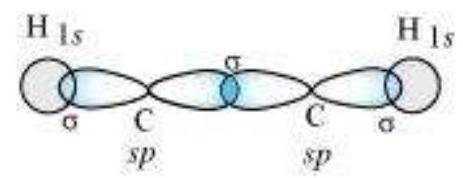
4.28 What is the total number of sigma and pi bonds in the following molecules?
(a) $\mathrm{C_2} \mathrm{H_2}$ (b) $\mathrm{C_2} \mathrm{H_4}$
Show Answer
Answer
A single bond is a result of the axial overlap of bonding orbitals. Hence, it contributes a sigma bond. A multiple bond (double or triple bond) is always formed as a result of the sidewise overlap of orbitals. A pi-bond is always present in it. A triple bond is a combination of two pi-bonds and one sigma bond.
Structure of $C_2 H_2$ can be represented as:
$H-\frac{\sigma}{\frac{\pi}{\sigma}} C \stackrel{\sigma}{-} H$
Hence, there are three sigma and two pi-bonds in $C_2 H_2$.
The structure of $C_2 H_4$ can be represented as:
Hence, there are five sigma bonds and one pi-bond in $C_2 H_4$.
4.29 Considering $x$-axis as the internuclear axis which out of the following will not form a sigma bond and why? (a) $1 \mathrm{~s}$ and $1 \mathrm{~s}$ (b) $1 \mathrm{~s}$ and $2 p_{\mathrm{x}}$; (c) $2 p_{\mathrm{y}}$ and $2 p_{\mathrm{y}}$ (d) $1 s$ and $2 s$.
Show Answer
Answer
$2 p_y$ and $2 p_y$ orbitals will not a form a sigma bond. Taking $x$-axis as the internuclear axis, $2 p_y$ and $2 p_y$ orbitals will undergo lateral overlapping, thereby forming a pi ( $\pi$ ) bond.
4.30 Which hybrid orbitals are used by carbon atoms in the following molecules? $\mathrm{CH_3}-\mathrm{CH_3}$; (b) $\mathrm{CH_3}-\mathrm{CH}=\mathrm{CH_2}$; (c) $\mathrm{CH_3}-\mathrm{CH_2}-\mathrm{OH}$; (d) $\mathrm{CH_3}-\mathrm{CHO}$ (e) $\mathrm{CH_3} \mathrm{COOH}$
Show Answer
Answer
(a)
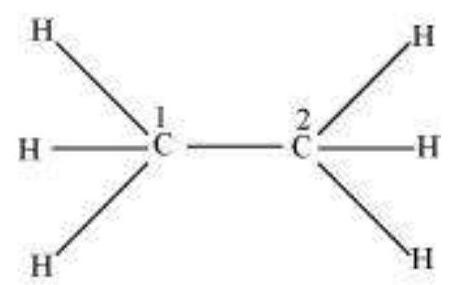
Both $C_1$ and $C_2$ are $s p^{3}$ hybridized.
(b)
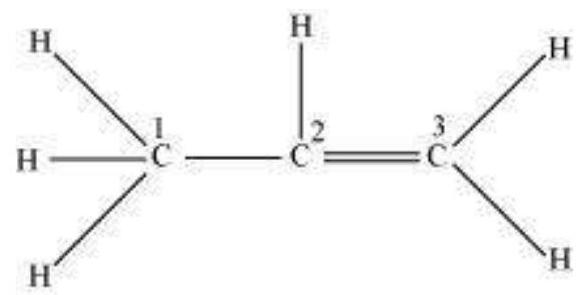
$C_1$ is $s p^{3}$ hybridized, while $C_2$ and $C_3$ are $s p^{2}$ hybridized.
(c)

Both $C_1$ and $C_2$ are $s p^{3}$ hybridized.
(d)
$C_1$ is $s p^{3}$ hybridized and $C_2$ is $s p^{2}$ hybridized.
(e)
 >
>
$C_1$ is $s p^{3}$ hybridized and $C_2$ is $s p^{2}$ hybridized.
4.31 What do you understand by bond pairs and lone pairs of electrons? Illustrate by giving one exmaple of each type.
Show Answer
Answer
When two atoms combine by sharing their one or more valence electrons, a covalent bond is formed between them.
The shared pairs of electrons present between the bonded atoms are called bond pairs. All valence electrons may not participate in bonding. The electron pairs that do not participate in bonding are called lone pairs of electrons.
For example, in $C_2 H_6$ (ethane), there are seven bond pairs but no lone pair present.
$\underset{\Large\mathrm{H}}{\Large\mathrm{C}}$
In $H_2 O$, there are two bond pairs and two lone pairs on the central atom (oxygen).
4.32 Distinguish between a sigma and a pi bond.
Show Answer
Answer
The following are the differences between sigma and pi-bonds:
| Sigma ( $ \sigma $) Bond | Pi $(\pi)$ Bond |
|---|---|
| (a) It is formed by the end to end overlap of orbitals. | It is formed by the lateral overlap of orbitals. |
| (b) The orbitals involved in the overlapping are $s -s, s- $p$, or $p - $p$. |
These bonds are formed by the overlap of $p - p$ orbitals only. |
| (c) It is a strong bond. | It is weak bond. |
| (d) The electron cloud is symmetrical about the line joining the two nuclei. |
The electron cloud is not symmetrical. |
| (e) It consists of one electron cloud, which is symmetrical about the internuclear axis. |
There are two electron clouds lying above and below the plane of the atomic nuclei. |
| (f) Free rotation about $\sigma $ bonds is possible. | Rotation is restricted in case of pi-bonds. |
4.33 Explain the formation of $\mathrm{H_2}$ molecule on the basis of valence bond theory.
Show Answer
Answer
Let us assume that two hydrogen atoms ( $A$ and $B$ ) with nuclei $(N_A.$ and $.N_B)$ and electrons $(e_A.$ and $.e_B)$ are taken to undergo a reaction to form a hydrogen molecule.
When $A$ and $B$ are at a large distance, there is no interaction between them. As they begin to approach each other, the attractive and repulsive forces start operating.
Attractive force arises between:
(a) Nucleus of one atom and its own electron i.e., $N_A-e_A$ and $N_B-e_B$.
(b) Nucleus of one atom and electron of another atom i.e., $N_A-e_B$ and $N_B-e_A$
Repulsive force arises between:
(a) Electrons of two atoms i.e., $e_A-e_B$
(b) Nuclei of two atoms i.e., $N_A-N_B$.
The force of attraction brings the two atoms together, whereas the force of repulsion tends to push them apart.
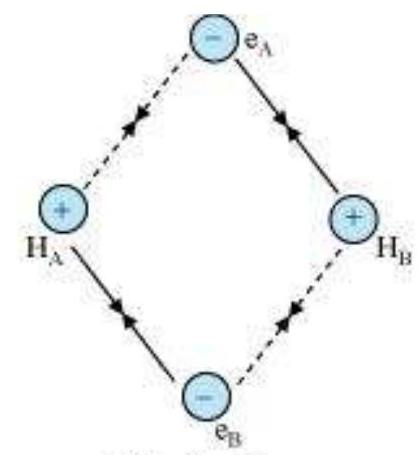
Attractive Forces
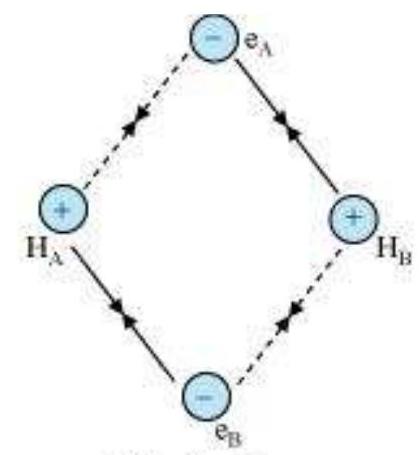
Repulsive Forces
The magnitude of the attractive forces is more than that of the repulsive forces. Hence, the two atoms approach each other. As a result, the potential energy decreases. Finally, a state is reached when the attractive forces balance the repulsive forces and the system acquires minimum energy. This leads to the formation of a dihydrogen molecule.
4.34 Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.
Show Answer
Answer
The given conditions should be satisfied by atomic orbitals to form molecular orbitals:
(a) The combining atomic orbitals must have the same or nearly the same energy. This means that in a homonuclear molecule, the 1s-atomic orbital of an atom can combine with the $1 s$-atomic orbital of another atom, and not with the 2s-orbital.
(b) The combining atomic orbitals must have proper orientations to ensure that the overlap is maximum.
(c) The extent of overlapping should be large.
4.35 Use molecular orbital theory to explain why the $\mathrm{Be_2}$ molecule does not exist.
Show Answer
Answer
The electronic configuration of Beryllium is $1 s^{2} 2 s^{2}$.
The molecular orbital electronic configuration for $Be_2$ molecule can be written as:
$\begin{matrix} \sigma_1^{2} & \sigma _{1 s}^{* 2} & \sigma_2^{2} & \sigma _{2 s}^{* 2}\end{matrix} $
Hence, the bond order for $Be_2$ is $\frac{1}{2}(N_b-N_a)$.
Where,
$N_b=$ Number of electrons in bonding orbitals
$N_a=$ Number of electrons in anti-bonding orbitals
$\therefore$ Bond order of $Be_2=\frac{1}{2}(4-4)=0$
A negative or zero bond order means that the molecule is unstable. Hence, $Be_2$ molecule does not exist.
4.36 Compare the relative stability of the following species and indicate their magnetic properties;
$\mathrm{O_2}, \mathrm{O}_2^{+}, \mathrm{O}_2^{-}$(superoxide), $\mathrm{O}_2^{2-}$ (peroxide)
Show Answer
Answer
There are 16 electrons in a molecule of dioxygen, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:
$ [\sigma - (1s)]^2 [\sigma^*(is)]^2 [\sigma (2s)]^2[\sigma (1p_z)]^2[\pi (2p_x)]_2[\pi (2p_y)]^2 [\pi(2p_x)]^1 [\pi (2p_y)]^1 $ Since the $1 s$ orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_b$ and the number of anti-bonding orbitals $=4=N _{\text{a }}$.
Bond order $=\frac{1}{2}(N_b-N_a)$
$=\frac{1}{2}(8-4)$
$=2$
Similarly, the electronic configuration of $O_2^{+}$can be written as:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi (2 p_x)]^{1}$
$N_b=8$
$N_a=3$
Bond order of $O_2^{+}=\frac{1}{2}(8-3)$ $=2.5$
Electronic configuration of $O_2^{-}$ion will be:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{1}$
$N_b=8$
$N_a=5$
Bond order of $O_2^{-}=\frac{1}{2}(8-5)$
$=1.5$
Electronic configuration of $O_2^{2-}$ ion will be:
$KK[\sigma(2 s)]^{2}[\sigma(2 s)]^{2}[\sigma(2 p_z)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}[\pi(2 p_x)]^{2}[\pi(2 p_y)]^{2}$
$N_b=8$
$N_a=6$
Bond order of $O_2^{2-}=\frac{1}{2}(8-6)$
$=1$
Bond dissociation energy is directly proportional to bond order. Thus, the higher the bond order, the greater will be the stability. On this basis, the order of stability is $O_2^{+}>O_2>O_2^{-}>O_2^{2-}$.
4.37 Write the significance of a plus and a minus sign shown in representing the orbitals.
Show Answer
Answer
Molecular orbitals are represented by wave functions. A plus sign in an orbital indicates a positive wave function while a minus sign in an orbital represents a negative wave function.
4.38 Describe the hybridisation in case of $\mathrm{PCl_5}$. Why are the axial bonds longer as compared to equatorial bonds?
Show Answer
Answer
The ground state and excited state outer electronic configurations of phosphorus $(Z=15)$ are:
Ground state:
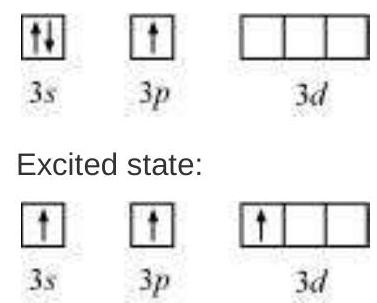
Phosphorus atom is $s p^{3} d$ hybridized in the excited state. These orbitals are filled by the electron pairs donated by five $Cl$ atoms as:
$PCl_5$
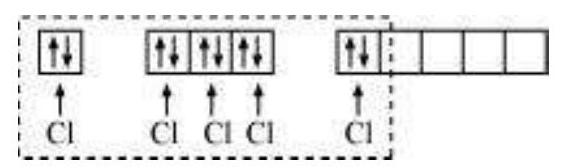
The five $s p^{3} d$ hybrid orbitals are directed towards the five corners of the trigonal bipyramidals. Hence, the geometry of $PCl_5$ can be represented as:
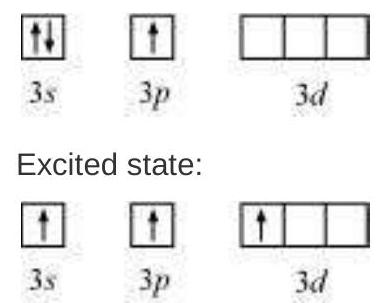
There are five $P-Cl$ sigma bonds in $PCl_5$. Three $P-Cl$ bonds lie in one plane and make an angle of $120^{\circ}$ with each other. These bonds are called equatorial bonds.
The remaining two $P-Cl$ bonds lie above and below the equatorial plane and make an angle of $90^{\circ}$ with the plane. These bonds are called axial bonds.
As the axial bond pairs suffer more repulsion from the equatorial bond pairs, axial bonds are slightly longer than equatorial bonds.
4.39 Define hydrogen bond. Is it weaker or stronger than the van der Waals forces?
Show Answer
Answer
A hydrogen bond is defined as an attractive force acting between the hydrogen attached to an electronegative atom of one molecule and an electronegative atom of a different molecule (may be of the same kind).
Due to a difference between electronegativities, the bond pair between hydrogen and the electronegative atom gets drifted far away from the hydrogen atom. As a result, a hydrogen atom becomes electropositive with respect to the other atom and acquires a positive charge. $4^{\delta}-X^{\delta-} \ldots \ldots . . H^{\delta+}-X^{\delta-} \ldots \ldots . . H^{\delta+}-X^{\delta-}$
The magnitude of $H$-bonding is maximum in the solid state and minimum in the gaseous state.
There are two types of $H$-bonds:
(i) Intermolecular $H$-bond e.g., $HF, H_2 O$ etc.
(ii) Intramolecular H-bond e.g., o-nitrophenol
Hydrogen bonds are stronger than Van der Walls forces since hydrogen bonds are regarded as an extreme form of dipole-dipole interaction.
4.40 What is meant by the term bond order? Calculate the bond order of : $\mathrm{N_2}, \mathrm{O_2}, \mathrm{O_2}^{+}$ and $\mathrm{O_2}^{-}$.
Show Answer
Answer
Bond order is defined as one half of the difference between the number of electrons present in the bonding and antibonding orbitals of a molecule.
If $N_a$ is equal to the number of electrons in an anti-bonding orbital, then $N_b$ is equal to the number of electrons in a bonding orbital.
Bond order $=\frac{1}{2}(N_b-N_a)$
If $N_b>N_a$, then the molecule is said be stable. However, if $N_b \leq N_a$, then the molecule is considered to be unstable.
Bond order of $N_2$ can be calculated from its electronic configuration as:
$\sigma(1s)^2 \sigma*(1s)2 \sigma(2s)^2 \sigma*(2s)2 \pi(2p_x)^2 \pi(2p_y)^2 \sigma(2p_z)^2$
Number of bonding electrons, $N_b=10$
Number of anti-bonding electrons, $N_a=4$
Bond order of nitrogen molecule $=\frac{1}{2}(10-4)$
$=3$
There are 16 electrons in a dioxygen molecule, 8 from each oxygen atom. The electronic configuration of oxygen molecule can be written as:
$ [ \sigma(1s)^2 \sigma*(1s)2 \sigma(2s)^2 \sigma*(2s)2 \sigma(1p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)1 \pi*(2p_y)1 ] $
Since the $1 s$ orbital of each oxygen atom is not involved in boding, the number of bonding electrons $=8=N_b$ and the number of anti-bonding electrons $=4=N _{\text{a }}$.
Bond order $=\frac{1}{2}(N_b-N_a)$
$=\frac{1}{2}(8-4)$
$=2$
Hence, the bond order of oxygen molecule is 2 .
Similarly, the electronic configuration of $O_2^{+}$can be written as:
$[ \sigma(2s)^2 \sigma*(2s)2 \sigma(2p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)1 ]$
$N_b=8$
$N_a=3$
Bond order of $O_2^{+}=\frac{1}{2}(8-3)$
$=2.5$
Thus, the bond order of $O_2^{+}$is 2.5.
The electronic configuration of $O_2^{-}$ion will be:
$ [ \sigma(2s)^2 \sigma*(2s)2 \sigma(2p_z)^2 \pi(2p_x)^2 \pi(2p_y)^2 \pi*(2p_x)2 \pi*(2p_y)1 ] $
$N_b=8$
$N_a=5$
Bond order of $O_2^{-}=\frac{1}{2}(8-5)$
$=1.5$
Thus, the bond order of $O_2^{-}$ion is 1.5.
“वैज्ञानिक निरंतर नए यौगिकों की खोज कर रहे हैं, उनके तथ्यों को क्रम में व्यवस्थित कर रहे हैं, विद्यमान जानकारी के आधार पर उनकी व्याख्या की कोशिश कर रहे हैं, नए तथ्यों की व्याख्या करने के लिए प्रचलित धारणाओं को संशोधित कर रहे हैं या नए सिद्धांतों को विकसित कर रहे हैं।”
द्रव्य एक या विभिन्न प्रकार के तत्त्वों से मिलकर बना होता है। सामान्य स्थितियों में उत्कृष्ट गैसों के अलावा कोई अन्य तत्त्व एक स्वतंत्र परमाणु के रूप में विद्यमान नहीं होता हैं। परमाणुओं के समूह विशिष्ट गुणों वाली स्पीशीज़ के रूप में विद्यमान होते हैं। परमाणुओं के ऐसे समूह को ‘अणु’ कहते हैं। प्रत्यक्ष रूप में कोई बल अणुओं के घटक परमाणुओं को आपस में पकड़े रहता है। विभिन्न रासायनिक स्पीशीज़ में उनके अनेक घटकों (परमाणुओं, आयनों इत्यादि) को संलग्न रखनेवाले आकर्षण बल को ‘रासायनिक आबंध’ कहते हैं। चूँकि रासायनिक यौगिक विभिन्न तत्त्वों के परमाणुओं की भिन्न-भिन्न विधिओं से संयुक्त होने के परिणामस्वरूप बनते हैं, अतः इससे कई प्रश्न उत्पन्न होते हैं। परमाणु संयुक्त क्यों होते हैं? केवल कुछ संयोजन ही संभव क्यों हैं? क्यों कुछ परमाणु संयुक्त होते हैं, जबकि कुछ अन्य ऐसा नहीं होते हैं? अणुओं की निश्चित आकृतियाँ क्यों होती हैं? इन सभी प्रश्नों के उत्तर देने के लिए समय-समय पर विभिन्न सिद्धांत सामने आए हैं। ये हैं कॉसेल-लूइस सिद्धांत, संयोजकता कक्ष इलेक्ट्रॉन युग्म प्रतिकर्षण (वी.एस.ई.पी.आर) सिद्धांत, संयोजकता आबंध सिद्धांत तथा आण्विक कक्षक सिद्धांत। संयोजकता के विभिन्न सिद्धांतों का विकास तथा रासायनिक आबंधों की प्रकृति की व्याख्या का सीधा संबंध वास्तव में परमाणु-संरचना तत्त्वों के इलेक्ट्रॉनिक विन्यास तथा आवर्त सारणी को समझने से रहा है। प्रत्येक निकाय अधिक स्थायी होने का प्रयास करता है। यह आबंधन स्थायित्व पाने के लिए ऊर्जा को कम करने का प्राकृतिक तरीका है।
4.1 रासायनिक आबंधन की कॉसेल-लूइस अवधारणा
इलेक्ट्रॉनों द्वारा रासायनिक आबंधों के बनने की व्याख्या के लिए कई प्रयास किए गए, लेकिन सन् 1916 में कॉसेल और लुइस स्वतंत्र रूप से संतोषजनक व्याख्या देने में सफल हुए। उन्होंने सर्वप्रथम संयोजकता (Valence) की तर्क संगत व्याख्या की। यह व्याख्या उत्कृष्ट गैसों की अक्रियता पर आधारित थी।
लूइस परमाणुओं को एक धन आवेशित अष्टि (आंतरिक इलेक्ट्रॉन एवं नाभिकयुक्त) तथा बाह्य कक्षकों के रूप में निरूपित किया। बाह्य कक्षकों में अधिकतम आठ इलेक्ट्रॉन समाहित हो सकते हैं। उसने यह भी माना कि ये आठों इलेक्ट्रॉन घन के आठों कोनों पर उपस्थित होते हैं, जो केंद्रीय अष्टि को चारों तरफ से घेरे रहते हैं। इस प्रकार सोडियम के बाह्य कक्ष में उपस्थित एकल इलेक्ट्रॉन घन के एक कोने पर स्थित रहता है, जबकि उत्कृष्ट गैसों में घन के आठों कोनों पर एक-एक इलेक्ट्रॉन उपस्थित रहते हैं। इलेक्ट्रॉनों का यह अष्टक एक विशेष स्थायी विन्यास निरूपित करता है। लूइस ने यह अभिगृहीत दिया कि परमाणु परस्पर रासायनिक आबंध द्वारा संयुक्त होकर अपने स्थायी अष्टक को प्राप्त करते हैं। उदाहरण के लिए- सोडियम एवं क्लोरीन में सोडियम अपना एक इलेक्ट्रॉन क्लोरीन को सरलतापूर्वक देकर अपना स्थायी अष्टक प्राप्त करता है तथा क्लोरीन एक इलेक्ट्रॉन प्राप्त कर अपना स्थायी अष्टक निर्मित करता है, अर्थात् सोडियम आयन $\left(\mathrm{Na}^{+}\right)$ एवं क्लोराइड आयन (Cl) बनते हैं। अन्य उदाहरणों (जैसे$\mathrm{Cl} _{2}, \mathrm{H} _{2}, \mathrm{~F} _{2}$, इत्यादि) में परमाणुओं में आबंध परस्पर इलेक्ट्रॉनों की सहभाजन द्वारा निर्मित होते हैं। इस प्रक्रिया द्वारा इन अणुओं के परमाणु एक बाह्य स्थायी अष्टक अवस्था प्राप्त करते हैं।
लूइस प्रतीक : किसी अणु के बनने में परमाणुओं के केवल बाह्य कोश इलेक्ट्रॉन रासायनिक संयोजन में हिस्सा लेते हैं। ये इनके संयोजकता इलेकट्रॉन (Valence Electron) कहलाते हैं। आंतरिक कोश इलेक्ट्रॉन (Inner Shell Electron) अच्छी प्रकार से सुरक्षित होते हैं तथा सामान्यतः संयोजन प्रक्रिया में सम्मिलित नहीं होते हैं। एक अमेरिकी रसायनज्ञ जी.एन. लूइस ने परमाणु में संयोजकता इलेक्ट्रॉनों को निरूपित करने के लिए सरल संकेतनों को प्रस्तावित किया, जिन्हें लूइस प्रतीक (Lewis Symbol) कहा जाता है। उदाहरणार्थ- दूसरे आवर्त के तत्त्वों के ‘लूइस प्रतीक’ इस प्रकार हैं-
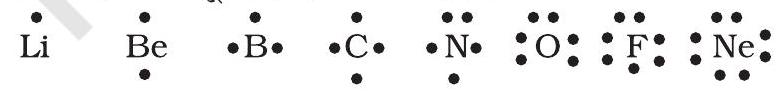
लूइस प्रतीकों का महत्त्व : प्रतीक के चारों ओर उपस्थित बिंदुओं की संख्या परमाणु के संयोजकता इलेक्ट्रॉनों की संख्या को दर्शाती है। यह संख्या तत्त्व की सामान्य अथवा समूह संयोजकता के परिकलन में सहायता देती है। तत्त्व की समूह संयोजकता या तो लूइस प्रतीक में उपस्थित बिंदुओं की संख्या के बराबर होती है या 8 में से बिंदुओं अथवा संयोजकता इलेक्ट्रॉनों की संख्या को घटाकर इसे परिकलित किया जा सकता है।
रासायनिक आबंधन के संबंध में कॉसेल ने निम्नलिखित तथ्यों की ओर ध्यान आकर्षित किया-
- आवर्त सारणी में उच्च विद्युत्-ऋणात्मकता वाले हैलोजेन तथा उच्च विद्युत्-धनात्मकता वाले क्षार धातु एक दूसरे से उत्कृष्ट गैसों द्वारा पृथक् रखे गए हैं।
- हैलोजेन परमाणुओं से ऋणायन तथा क्षार से धनायन का निर्माण संबंधित परमाणुओं द्वारा क्रमशः एक इलेक्ट्रॉन ग्रहण करने तथा एक इलेक्ट्रॉन मुक्त होने के फलस्वरूप होता है।
- इस प्रकार निर्मित ऋणायन तथा धनायन उत्कृष्ट गैस के स्थायी इलेक्ट्रॉनिक विन्यास को प्राप्त करते हैं। उत्कृष्ट गैसों में बाह्यतम कोश का आठ इलेक्ट्रॉनों वाला (अष्टक) विन्यास $n s^{2} n p^{6}$, विशेष रूप से स्थायी होता है। हीलियम इसका अपवाद है, जिसके बाह्यतम कोश में केवल दो इलेक्ट्रॉन (डयूप्लेट) होते हैं।
- ऋणायन तथा धनायन स्थिर वैद्युत आकर्षण द्वारा स्थायित्व ग्रहण करते हैं।
उदाहरणार्थ- उपर्युक्त सिद्धांत के अनुसार, सोडियम तथा क्लोरीन से $\mathrm{NaCl}$ का बनना निम्नलिखित रूप में दर्शाया जा सकता है-
| $\mathrm{Na}$ | $\rightarrow$ | $\mathrm{Na}^{+}+\mathrm{e}^{-}$ |
| $[\mathrm{Ne}] 3 \mathrm{~s}^{1}$ | $[\mathrm{Ne}]$ | |
| $\mathrm{Cl}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{Cl}^{-}$ |
| $[\mathrm{Ne}] 3 s^{2} 3 p^{5}$ | $[\mathrm{Ne}] 3 s^{2} 3 p^{6}$ or $[\mathrm{Ar}]$ | |
| $\mathrm{Na}^{+}+\mathrm{Cl}^{-}$ | $\rightarrow$ | $\mathrm{NaCl}$ or $\mathrm{Na}^{+} \mathrm{Cl}^{-}$ |
$\mathrm{CaF} _{2}$ का बनना इस प्रकार दर्शाया जा सकता है-
| $\mathrm{Ca}$ | $\rightarrow$ | $\mathrm{Ca}^{2+}+2 \mathrm{e}^{-}$ |
| $[\mathrm{Ar}] 4 s^{2}$ | $[\mathrm{Ar}]$ | |
| $\mathrm{F}+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{F}^{-}$ |
| $[\mathrm{He}] 2 s^{2} 2 p^{5}$ | $[\mathrm{He}] 2 s^{2} 2 p^{6}$ or $[\mathrm{Ne}]$ | |
| $\mathrm{Ca}^{2+}+2 \mathrm{~F}^{-}$ | $\rightarrow$ | $\mathrm{CaF}_2$ or $\mathrm{Ca}^{2+}\left(\mathrm{F}^{-}\right)_2$ |
धनायन तथा ऋणायन के बीच आकर्षण के फलस्वरूप निर्मित आबंध को ‘वैद्युत् संयोजक आबंध’ (Electrovalent Bond) का नाम दिया गया। इस प्रकार वैद्युत संयोजकता (Electrovalency) आयन पर उपस्थित आवेश की इकाइयों की संख्या के बराबर होती है। अतः कैल्सियम की धनात्मक वैद्युत संयोजकता दो हैं, जबकि क्लोरीन की ऋणात्मक संयोजकता एक है।
इलेक्ट्रॉन स्थानांतरण द्वारा आयन का बनना तथा आयनिक क्रिस्टलीय यौगिकों के बनने के बारे में आधुनिक संकल्पनाएँ कॉसेल की अभिगृहीतों (Postulates) पर आधारित हैं। आयनिक यौगिकों के व्यवहार को समझने तथा उनको क्रमबद्ध करने में कॉसेल के विचारों से उल्लेखनीय सहायता मिली। साथ ही साथ उन्होंने इस तथ्य को भी स्वीकार किया है कि अनेक यौगिक उनकी अवधारणाओं के अनुरूप नहीं थे।
4.1.1 अष्टक् नियम (Octet Rule)
सन् 1916 में कॉसेल तथा लूइस ने परमाणुओं के बीच रासायनिक संयोजन के एक महत्त्वपूर्ण सिद्धांत को विकसित किया। इसे ‘रासायनिक आबंधन का इलेक्ट्रॉनिकी सिद्धांत’ कहा जाता है। इस सिद्धांत के अनुसार, परमाणुओं का संयोजन संयोजक इलेक्ट्रॉनों के एक परमाणु से दूसरे परमाणु पर स्थानांतरण के द्वारा अथवा संयोजक इलेक्ट्रॉनों के सहभाजन (Sharing) के द्वारा होता है। इस प्रक्रिया में परमाणु अपने संयोजकता कोश में अष्टक प्राप्त करते हैं। इसे ‘अष्टक नियम’ कहते हैं।
4.1.2 सहसंयोजी आबंध
सन् 1919 में लैंगम्यूर ने लूइस अभिगृहीतिओं में संशोधन किया। उन्होंने स्थिर घनीय अष्टक की आवधारणा का परित्याग किया तथा ‘सहसंयोजक आबंध’ (Covalent Bond) का प्रयोग किया। लूइस-लैंगम्यूर के सिद्धांत को क्लोरीन अणु $\left(\mathrm{Cl} _{2}\right)$ बनने के उदाहरण से समझा जा सकता है। क्लोरीन परमाणु का इलेक्ट्रॉनिक विन्यास $[\mathrm{Ne}] 3 s^{2} 3 p^{5}$ है, अर्थात् क्लोरीन परमाणु में ऑर्गन के विन्यास को प्राप्त करने के लिए एक इलेक्ट्रॉन की कमी है। $\mathrm{Cl} _{2}$ अणु के बनने को दो क्लोरीन परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के सहभाजन के रूप में समझा जा सकता है। इस प्रक्रिया में दोनों क्लोरीन परमाणु सहभाजित इलेक्ट्रॉन युग्म में एक-एक इलेक्ट्रॉन का योगदान करते हैं तथा इनके बाहय कोश करीबी उत्कृष्ट गैस, अर्थात् ऑर्गन का अष्टक विन्यास प्राप्त कर लेते हैं।

दो क्लोरीन परमाणुओं के बीच सहसंयोजी आबंध
यहाँ बिंदु इलेक्ट्रॉनों को निरूपित करते हैं। ये संरचनाएँ ‘लूइस बिंदु संरचनाएँ’ कहलाती हैं।
अन्य अणुओं के लिए भी लूइस बिंदु संरचनाएँ लिखी जा सकती हैं, जिनमें संयुक्त होने वाले परमाणु समान अथवा भिन्न हो सकते हैं। इसके लिए मुख्य नियम निम्नलिखित हैं-
- प्रत्येक आबंध का निर्माण परमाणुओं के मध्य एक इलेक्ट्रॉन युग्म के सहभाजन के फलस्वरूप होता है।
- संयुक्त होने वाला प्रत्येक परमाणु सहभाजित युग्म में एक-एक इलेक्ट्रॉन का योगदान देता है।
- इलेक्ट्रॉनों के सहभाजन के फलस्वरूप संयुक्त होने वाले परमाणु अपने बाहय कोश में उत्कृष्ट गैस विन्यास प्राप्त कर लेते हैं।
- इस प्रकार, जल तथा कार्बन टेट्राक्लोराइड के अणुओं में आबंधों के निर्माण को हम इस प्रकार निरूपित कर सकते हैं-

एक इलेक्ट्रॉन युग्म द्वारा संयुग्मित दो परमाणु एकल सहसंयोजी आबंध (Single Covalent Bond) द्वारा आबंधित कहलाते हैं। कई यौगिकों में परमाणुओं के बीच बहु- आबंध (Multiple Bonds) उपस्थित होते हैं। बहु-आबधों का निर्माण दो परमाणुओं के मध्य एक से अधिक इलेक्ट्रॉन युग्मों के सहभाजन के फलस्वरूप होता है। दो परमाणुओं के मध्य यदि दो इलेक्ट्रॉन युग्मों का सहभाजन होता है, तो उनके बीच का सहसंयोजी आबंध ‘द्वि-आबंध’ (Double Bond) कहलाता है। उदाहरणार्थ- कार्बन डाइ- ऑक्साइड अणु में कार्बन तथा ऑक्सीजन परमाणुओं के मध्य दो द्वि-आबंध उपस्थित होते हैं। इसी प्रकार एथीन (Ethene) के अणु में दो कार्बन परमाणु एक द्वि-आबंध द्वारा बंधित होते हैं।

$\mathrm{C} _{2} \mathrm{H} _{4}$ अणु
जब संयोजी परमाणुओं के मध्य तीन इलेक्ट्रॉन युग्मों का सहभाजन होता है, जैसा $\mathbf{N} _{2}$ अणु के दो नाइट्रोजन परमाणुओं के मध्य या एथाइन में दो कार्बन परमाणुओं के मध्य है, तब उनके मध्य एक त्रि-आबंध बनता है।

4.1.3 सरल अणुओं का लूइस निरूपण ( लूइस संरचाएँ )
लूइस बिंदु संरचनाओं द्वारा सहभाजित इलेक्ट्रॉन युग्मों तथा अष्टक नियम के अनुसार अणुओं एवं आयनों में आबंधन का चित्रण किया जाता है। यद्यपि यह चित्रण अणु में आबंधन तथा उसकी प्रकृति को पूर्ण रूप से स्पष्ट नहीं करता, परंतु इसके आधार पर अणु के विरचन (Formation) तथा उसके गुणों को पर्याप्त सीमा तक समझने में सहायता मिलती है। अतः अणुओं की लूइस बिंदु संरचनाएँ अत्यंत उपयोगी होती हैं। इन्हें निम्नलिखित पदों के आधार पर लिखा जा सकता है।
- लूइस संरचना लिखने के लिए आवश्यक कुल इलेक्ट्रॉनों की संख्या संयुग्मित होने वाले परमाणुओं के संयोजकताइलेक्ट्रॉनों के योग द्वारा प्राप्त की जाती है। उदाहरणार्थ$\mathrm{CH} _{4}$ अणु में कुल आठ संयोजकता इलेक्ट्रॉन (4 कार्बन परमाणु से तथा 4 हाइड्रोजन के चार परमाणुओं से) उपलब्ध होते हैं।
- संयोजकता इलेक्ट्रॉनों की कुल संख्या में ऋणायनों के लिए प्रति ऋणावेश एक इलेक्ट्रॉन जोड़ दिया जाता है, जबकि धनायनों के लिए प्रति धनावेश एक इलेक्ट्रॉन घटा दिया जाता है। उदाहरणार्थ- $\mathrm{CO} _{3}^{2-}$ आयन के लिए कार्बन तथा ऑक्सीजन के संयोजकता-इलेक्ट्रॉनों के योग में दो इलेक्ट्रॉन जोड़ दिए जाते हैं $\mathrm{CO} _{3}^{2-}$ आयन पर उपस्थित दो ऋणावेश यह दर्शाते हैं कि इस आयन में उदासीन परमाणुओं द्वारा दिए गए संयोजी इलेक्ट्रॉनों से दो इलेक्ट्रॉन अधिक हैं। $\mathrm{NH} _{4}^{+}$आयन पर उपस्थित +1 आवेश एक इलेक्ट्रॉन की हानि को दर्शाता है। अत: $\mathrm{NH} _{4}^{+}$आयन के लिए उदासीन परमाणुओं द्वारा दिए गए संयोजी इलेक्ट्रॉनों में से एक इलेक्ट्रॉन घटाया जाता है।
- संयुक्त होने वाले परमाणुओं के रासायनिक प्रतीकों तथा अणु की आधारभूत संरचना (Skeletal Structure), अर्थात कौन से परमाणु किन परमाणुओं के साथ आबंधित हैं- इस बात का ज्ञान होने पर परमाणुओं के बीच सभी इलेक्ट्रॉनों का वितरण आबंधित सहभाजी इलेक्ट्रॉन युग्मों के रूप में तथा संपूर्ण आबंधों की संख्या के अनुपात में सरल हो जाता है।
- सामान्यतः अणु में न्यूनतम विद्युत् ऋणात्मकता वाला परमाणु केंद्रीय परमाणु का स्थान पाता है। हाइड्रोजन तथा फ्लुओरीन के परमाणु साधारणतया अंतस्थ स्थान (Terminal Position) पाते हैं। जैसे $\mathrm{NF} _{3}$ तथा $\mathrm{CO} _{3}^{2-}$ में क्रमशः नाइट्रोजन तथा कार्बन केंद्रीय परमाणु के रूप में लिखे जाएँगे।
- एकल आबंधों के लिए सहभाजित इलेक्ट्रॉन युग्म लिखने के पश्चात् शेष इलेक्ट्रॉन युग्मों का उपयोग या तो बहुआबंधन के लिए किया जाता है या वे एकाकी इलेक्ट्रॉन युग्मों के रूप में रहते हैं। आधारभूत आवश्यकता यह है कि प्रत्येक आबंधित परमाणु में इलेक्ट्रॉनों का ऑक्टेट (अष्टक) पूरा हो जाए।
कुछ अणुओं तथा आयनों की लूइस बिंदु संरचनाओं को सारणी 4.1 में दिया गया है।
सारणी 4.1 कुछ अणुओं तथा आयनों की लुइस संरचनाएँ

उदाहरण 4.1
$\mathrm{CO}$ के अणु की लूइस बिंदु संरचना लिखें।
हल
पद 1 : कार्बन तथा ऑक्सीजन परमाणुओं के संयोजी इलेक्ट्रॉनों की कुल संख्या की गणना : कार्बन तथा ऑक्सीजन परमाणुओं के बाहय (संयोजकता) कोश के विन्यास क्रमशः $2 s^{2} 2 p^{2}$ तथा $2 s^{2} 2 p^{4}$ हैं। अतः उपलब्ध संयोजकता इलेक्ट्रॉनों की संख्या $=4+6=10$
पद 2: $\mathrm{CO}$ की आधारभूत संरचना : $\mathrm{CO}$
पद 3: $C$ तथा $O$ के बीच एक एकल आबंध बनाएँ (अर्थात् एक सहभाजित इलेक्ट्रॉन युग्म लिखें) ऑक्सीजन के परमाणु पर अष्टक पूर्ण करें। बचे हुए दो इलेक्ट्रॉन, $\mathrm{C}$ पर एकाकी इलेक्ट्रॉन युग्म के रूप में दर्शाएँ
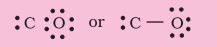
परंतु इस संरचना में कार्बन का अष्टक पूर्ण नहीं होता है। इसलिए $\mathrm{C}$ तथा $\mathrm{O}$ के नीच बहु-आबंध की आवश्यकता होती है। इन परमाणुओं के मध्य त्रि-आबंध लिखने पर दोनों परमाणुओं के लिए अष्टक नियम का पालन हो जाता है।
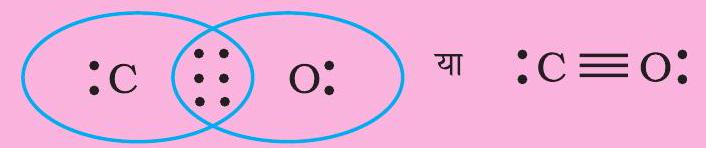
उदाहरण 4.2
नाइट्राइट आयन, $\mathrm{NO} _{2}^{-}$के लिए ’ लूइस संरचना’ लिखें। हल
हल
पद 1 : नाइट्रोजन तथा ऑक्सीजन परमाणुओं के संयोजकता इलेक्ट्रॉनों की संख्या-
$$ \begin{aligned} & \mathrm{N}\left(2 s^{2} 2 p^{3}\right), \mathrm{O}\left(2 s^{2} 2 p^{4}\right) \\ & 5+(2 \times 6)+ = 17 \text { इलेक्ट्रॉन } \end{aligned} $$
इकाई ऋणावेश के लिए एक इलेक्ट्रॉन जमा करने पर इलेक्ट्रॉनों की कुल संख्या = 17+1=18
पद 2: $\mathrm{NO} _{2}^{-}$आयन की आधारमूत संरचना को हम इस प्रकार लिख सकते हैं- $\mathrm{O} \quad \mathrm{N} \quad \mathrm{O}$
पद 3: नाइट्रोजन तथा प्रत्येक ऑक्सीजन के बीच एक एक आबंध बनाने (अर्थात् एक सहभाजित इलेक्ट्रॉन युग्म लिखने ) तथा ऑक्सीजन के परमाणुओं के अष्टक पूर्ण करने पर नाइट्रोजन पर उपस्थित दो इलेक्ट्रॉन एक एकाकी इलेक्ट्रॉन युग्म बनाते हैं।

चूँकि इस प्रकार नाइट्रोजन परमाणु पर अष्टक पूर्ण नहीं होता है। इसलिए $N$ तथा $O$ के बीच बहु-आबंध की आवश्यकता होती है। नाइट्रोजन तथा ऑक्सीजन के किसी एक परमाणु के बीच एक द्वि-आबंध बनाने पर हमें निम्नलिखित लूइस बिंदु संरचना प्राप्त होती है-

4.1.4 फॉर्मल आवेश
लूइस बिंदु संरचनाएँ सामान्यतः अणुओं की वास्तविक आकृति नहीं दर्शाती हैं। बहु-परमाणुक आयनों में संपूर्ण आवेश किसी विशेष परमाणु पर उपस्थित न होकर पूरे आयन पर स्थित होता है। हालाँकि प्रत्येक परमाणु पर फॉर्मल आवेश दर्शाया जा सकता है। बहुपरमाणुक अणु या आयन के किसी परमाणु पर उपस्थित फॉर्मल आवेश दर्शाया जा सकता है। बहुपरमाणुक अणु या आयन के किसी परमाणु पर उपस्थित फॉर्मल आवेश को उसके विगलित (Isolated) स्थिति (अर्थात् मुक्त परमाणु अवस्था) में संयोजकता इलेक्ट्रॉनों की कुल संख्या तथा लूइस संरचना में परमाणु को प्रदत्त इलेक्ट्रॉनों की संख्या के अंतर के रूप में परिभाषित किया जा सकता है। इसे इस प्रकार अभिव्यक्त किया जाता है-

फॉर्मल आवेश का परिकलन इस अवधारणा पर आधारित है कि अणु अथवा आयन में संबंधित परमाणु पर प्रत्येक सहभाजित युग्म में से एक इलेक्ट्रॉन तथा एकाकी युग्म के दोनों इलेक्ट्रॉन उपस्थित रहते हैं।
आइए, ओज़ोन $\left(\mathrm{O} _{3}\right)$ के अणु को लें। $\mathrm{O} _{3}$ की लूइस संरचना को इस प्रकार लिखा जा सकता है-

ऑक्सीजन के परमाणुओं को 1,2 तथा 3 द्वारा चिह्नित किया गया है-
- 1 द्वारा चिह्नित केंद्रीय $\mathrm{O}$ परमाणु पर फॉर्मल आवेश $=6-2-\frac{1}{2}(6)=1$
- 2 द्वारा चिह्नित अंतस्थ $\mathrm{O}$ परमाणु पर फॉर्मल आवेश $=6-4-\frac{1}{2}(4)=0$
- 3 द्वारा चिह्नित अंतस्थ $\mathrm{O}$ परमाणु पर फॉर्मल आवेश $=6-6-\frac{1}{2}(2)=-1$
अतः $\mathrm{O} _{3}$ के अणु को फॉर्मल आवेश के साथ इस प्रकार दर्शाया जाता है-

यहाँ पर ध्यान देने योग्य बात यह है कि फॉर्मल आवेश, अणु में वास्तविक आवेश पृथकन प्रकट नहीं करते हैं। लूइससंरचना में परमाणुओं पर आवेश को दर्शाने से अणु में संयोजकता इलेक्ट्रॉनों को लेखा-जोखा रखने में सहायता मिलती है। फॉर्मल आवेश की सहायता से किसी स्पीशीज़ की कई संभव लूइस संरचनाओं में से निम्नतम ऊर्जा की संरचना का चयन करने में सहायता मिलती है। साधारणतः न्यूनतम ऊर्जा वाली संरचना वह होती है, जिसके परमाणुओं पर न्यूनतम फॉर्मल आवेश हो। फॉर्मल आवेश का सिद्धांत आबंधन की शुद्ध सहसंयोजी प्रकृति पर आधारित है, जिसमें आबंधित परमाणुओं के मध्य इलेक्ट्रॉनों का सहभाजन समान रूप से होता है।
4.1.5 अष्टक नियम की सीमाएँ
यद्यपि अष्टक नियम अत्यंत उपयोगी है, परंतु यह सदैव लागू नहीं किया जा सकता है। यह मुख्य रूप से आवर्त सारणी के द्वितीय आवर्त के तत्त्वों पर लागू होता है तथा अधिकांश कार्बनिक यौगिकों की संरचनाओं को समझने में उपयोगी होता है। अष्टक नियम के तीन प्रमुख अपवाद हैं-
केंद्रीय परमाणु का अपूर्ण अष्टक
कुछ यौगिकों में केंद्रीय परमाणु के चारों ओर उपस्थित इलेक्ट्रॉनों की संख्या आठ से कम होती है। यह मुख्यतः उन तत्त्वों के यौगिकों में होता है, जिनमें संयोजकता इलेक्ट्रॉनों की संख्या चार से कम होती है। उदाहरण के लिए- $\mathrm{LiCl}, \mathrm{BeH} _{2}$ तथा $\mathrm{BCl} _{3}$ लेते हैं।
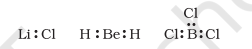
यहाँ पर $\mathrm{Li}, \mathrm{Be}$ तथा $\mathrm{B}$ के संयोजकता इलेक्ट्रॉनों की संख्या क्रमशः 1,2 तथा 3 है। इस प्रकार के अन्य यौगिक $\mathrm{AlCl} _{3}$ तथा $\mathrm{BF} _{3}$ हैं।
विषम इलेक्ट्रॉन (Odd-Electron) अणु
उन अणुओं जिनमें इलेक्ट्रॉनों की कुल संख्या विषम (Odd) होती है (जैसे-नाइट्रिक ऑक्साइड, $\mathrm{NO}$ तथा नाइट्रोजन डाइऑक्साइड, $\mathrm{NO} _{2}$ ), में सभी परमाणु अष्टक नियम का पालन नहीं कर पाते।
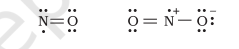
प्रसारित (Expanded) अष्टक
आवर्त सारणी के तीसरे तथा इसके आगे के आवर्तों के तत्त्वों में आबंधन के लिए $3 s$ तथा $3 p$ कक्षकों के अतिरिक्त $3 d$ कक्षक भी उपलब्ध होते हैं। इन तत्त्वों के अनेक यौगिकों में केंद्रीय परमाणु के चारों ओर आठ से अधिक इलेक्ट्रॉन होते हैं। इसे प्रसारित अष्टक (Expanded Octet) कहते हैं। स्पष्ट है कि इन यौगिकों पर अष्टक नियम लागू नहीं होता है।
ऐसे यौगिकों के कुछ उदाहरण हैं- $\mathrm{PF} _{5}, \mathrm{SF} _{6}, \mathrm{H} _{2} \mathrm{SO} _{4}$ तथा कई उपसहसंयोजी यौगिक।

रोचक तथ्य यह है कि सल्फर परमाणु ऐसे अनेक यौगिक भी बनाता है, जिनमें अष्टक नियम का पालन होता है। उदाहरणार्थ- सल्फर डाइक्लोराइड में $\mathrm{S}$ परमाणु के चारों ओर इलेक्ट्रॉनों का अष्टक उपस्थित होता है।
अष्टक नियम की कुछ अन्य कमियाँ
- यह स्पष्ट है कि अष्टक नियम उत्कृष्ट गैसों की रासायनिक अक्रियता पर आधारित है, परंतु कुछ उत्कृष्ट गैसें (जैसे- ज़ीनॉन तथा क्रिप्टॉन) ऑक्सीजन तथा फ्लुओरीन से भी संयोजित होती हैं तथा कई यौगिक बनाती हैं। जैसे- $\mathrm{XeF} _{2}, \mathrm{KrF} _{2}, \mathrm{XeOF} _{2}$ इत्यादि।
- अष्टक सिद्धांत अणु की आकृति स्पष्ट नहीं करता है।
- यह अणु की ऊर्जा, अर्थात् उसके सापेक्ष स्थायित्व के बारे में कुछ भी संकेत नहीं देता है।
4.2 आयनिक या वैद्युत् संयोजी आबंध
आयनिक आबंध विरचन की कॉसेल तथा लूइस अवधारणा से यह निष्कर्ष निकलता है कि इस आबंध का विरचन मुख्य रूप से निम्नलिखित तथ्यों निर्भर करेगा-
- उदासीन परमाणु से संबंधित धनायनों एवं ऋणायनों के बनने की सरलता तथा
- धनायनों एवं ऋणायनों की ठोस में व्यवस्थित होने की विधि, अर्थात् क्रिस्टलीय यौगिक का जालक (Lattice) निर्मित होने की विधि।
धनायन का बनना आयनीकरण, अर्थात् उदासीन परमाणु में से एक या एक से अधिक इलेक्ट्रॉनों के निष्कासन द्वारा संपन्न होता है। इसी प्रकार उदासीन परमाणु द्वारा इलेक्ट्रॉन ग्रहण करने से ऋणायन प्राप्त होता है।
| $\mathrm{M}(\mathrm{g}) $ | $\rightarrow$ | $\mathrm{M}^{+}(\mathrm{g})+\mathrm{e}^{-} ;$ | |
| आयनन एंथैल्पी | |||
| $\mathrm{X}(\mathrm{g})+\mathrm{e}^{-}$ | $\rightarrow$ | $\mathrm{X}^{-}(\mathrm{g}) ;$ | |
| इलेक्ट्रॉन लब्धि एंथैल्पी | |||
| $\mathrm{M}^{+}(\mathrm{g})+\mathrm{X}^{-}(\mathrm{g}) \rightarrow$ | $\mathrm{MX}(\mathrm{s})$ |
इलेक्ट्रॉन लब्धि एंथैल्पी, $\Delta_{\mathrm{eg}} H$, गैस प्रावस्था में परमाणु द्वारा एक इलेक्ट्रॉन ग्रहण करने के फलस्वरूप होने वाला एंथैल्पी परिवर्तन है (एकक 3)। इलेक्ट्रॉन लब्धि प्रकिया ऊष्माशोषी अथवा उष्माक्षेपी हो सकती है। दूसरी ओर आयनन सदैव ऊष्माशोषी ही होता है। इलेक्ट्रॉन-लब्धि के फलस्वरूप होने वाले ऊर्जा-परिवर्तन का ऋणात्मक मान इलेक्ट्रॉन बंधुता (Electron Affinity) होता है।
यह स्पष्ट है कि आयनिक आबंध निम्न आयनन एंथैल्पी तथा अपेक्षाकृत निम्न इलेक्ट्रॉन लब्धि एंथैल्पी वाले तत्त्वों के बीच अधिक सरलता से बनते हैं।
अधिकांश आयनिक यौगिकों के धनायन धात्विक तत्त्वों से तथा ऋणायन अधात्विक तत्त्वों से निर्मित होते हैं। दो अधात्विक तत्त्वों से बनने वाला अमोनियम आयन एक अपवाद है। यह अनेक यौगिकों में धनायन के रूप में होता है।
आयनिक यौगिकों के क्रिस्टल में धनायन तथा ऋणायन त्रिविमीय रूप में नियमित रूप से व्यवस्थित रहते हैं। ये आयन कूलामी अन्योन्य (Coulombic Interaction) बलों द्वारा परस्पर जुड़े रहते हैं। आयनों के आकार उनके नियचन (Packing) क्रम तथा अन्य कारणों के आधार पर ये यौगिक विभिन्न क्रिस्टलीय संरचनाओं में क्रिस्टलित होते हैं। उदाहरण के लिए-सोडियम क्लोराइड, $\mathrm{NaCl}$ (खनिज नमक) की क्रिस्टल संरचना नीचे दर्शाई गई है।
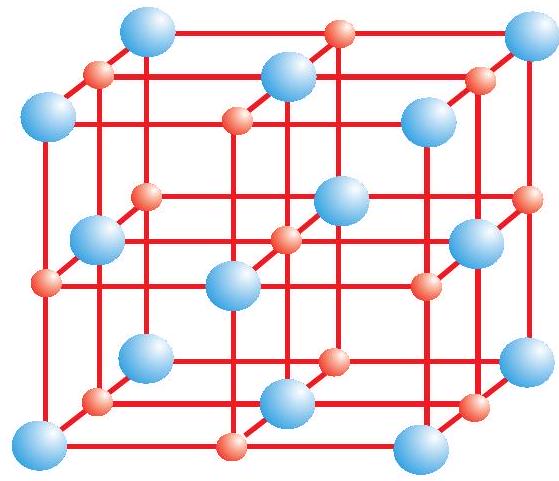
खनिज नमक संरचना
आयनिक ठोस के लिए इलेक्ट्रॉन लब्धि एंथैल्पी तथा आयनन एंथैल्पी का योग धनात्मक हो सकता है। ऐसे में क्रिस्टल संरचना का स्थायित्व उसके जालक के बनने में उत्पन्न मुक्त ऊर्जा के कारण होता है। उदाहरण के लिए$\mathrm{Na}$ धातु से $\mathrm{Na}^{+}$आयन के बनने की आयनन ऊर्जा 495.8 $\mathrm{kJ} \mathrm{mol}^{-1}$ है, जबकि $\mathrm{Cl}(\mathrm{g})$ से $\mathrm{Cl}^{-}(\mathrm{g})$ बनने की इलेक्ट्रॉन लब्धि एन्थैल्पी केवल $-348.7 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। इन दोनों का मान $147.1 \mathrm{~kJ}$ होता है। यह परिमाण (Value) सोडियम क्लोराइड के विरचन जालक एन्थैल्पी के मान $(-788 \mathrm{~J})$ की अपेक्षा अधिक प्रतिपूरित होती है। इसी प्रकार संपूर्ण प्रक्रमों से प्राप्त होने वाली ऊर्जा शोषित ऊर्जा से कहीं अधिक होती है। अतः किसी आयनिक यौगिक के स्थायित्व का गुणात्मक मान उस यौगिक के विरचन जालक एन्थैल्पी के ऊपर निर्भर करती है, न कि गैसीय अवस्था में उस आयनिक स्पीशीज़ द्वारा ऑक्टेट प्राप्ति पर।
चूँकि आयनिक यौगिकों के विरचन में जालक एन्थैल्पी महत्त्वपूर्ण भूमिका निभाती है; अतः आइए, हम इस विषय में कुछ और जानकारी प्राप्त करें।
4.2.1 जालक एन्थैल्पी (जालक ऊर्जा)
किसी आयनिक ठोस के एक मोल यौगिक को गैसीय अवस्था में संघटक आयनों में पृथक करने के लिए आवश्यक ऊर्जा को उस यौगिक की ‘जालक एन्थैल्पी’ कहते है। उदाहरण के लिए- $\mathrm{NaCl}$ की जालक एन्थैल्पी $788 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। इसका अर्थ यह है कि एक मोल ठोस $\mathrm{NaCl}$ को एक मोल $\mathrm{Na}^{+}(\mathrm{g})$ तथा एक मोल $\mathrm{Cl}^{-}(\mathrm{g})$ में अनंत दूरी तक पृथक् करने के लिए $788 \mathrm{~kJ}$ ऊर्जा की आवश्यकता होती है।
इस प्रक्रिया में विपरीत आवेश वाले आयनों में आकर्षक बल तथा समान आवेश वाले आयनों में प्रतिकर्षण बल-दोनों भाग लेते हैं। चूँकि ठोस क्रिस्टल त्रिविभीय होता है, अत: केवल आकर्षण तथा प्रतिकर्षण बलों की अन्योन्य क्रिया से ही जालक एन्थैल्पी का परिकलन करना संभव नहीं है। क्रिस्टल ज्यामिति से संबंधित कारकों को भी इसमें सम्मिलित करना आवश्यक है।
4.3 आबंध प्राचल
4.3.1 आबंध लंबाई
किसी अणु में आबंधित परमाणुओं के नाभिकों के बीच साम्यावस्था दूरी ‘आबंध लंबाई’ कहलाती है। आबंध लंबाई स्पेक्ट्रमी, एक्स-किरण विवर्तन तथा इलेक्ट्रॉन विवर्तन (Elec- tron Diffraction) विधियों की सहायता से ज्ञात की जाती है। इन तकनीकों का अध्ययन आप उच्च कक्षाओं में करेंगे। आबंधित युग्म का प्रत्येक परमाणु आबंध-लंबाई में योगदान देता है (चित्र 4.1)। सहसंयोजी आबंध में प्रत्येक परमाणु का योगदान उस परमाणु की ‘सहसंयोजी त्रिज्या’ कहलाती है।
आबंधित अवस्था में किसी परमाणु के क्रोड, जो संलग्न परमाणु के क्रोड के संपर्क में होता है, की त्रिज्या उसकी सहसंयोजी त्रिज्या मानी जाती है। सहसंयोजी त्रिज्या एक ही अणु में आबंधित दो समरूप परमाणुओं के बीच की दूरी का आधा भाग होती है।
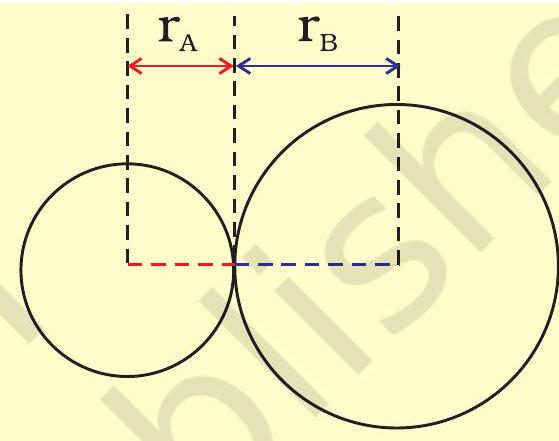
चित्र 4.1: सहसंयोजी अणु $A B$ में आबंध लंबाई $R=r_{A}+r_{B}$, जहाँ $R$ आबंध लंबाई है तथा $r_{A}$ व $r_{B}$ क्रमशः $A$ व $B$ परमाणुओं की सहसंयोजी त्रिज्याएँ हैं।
वांडरवाल त्रिज्या अनाबंधित अवस्था में संयोजी कोश सहित परमाणु का समग्र आकार निरूपित करती है। वांडरवाल त्रिज्या ठोस अवस्था में विभिन्न अणुओं के दो समरूप परमाणुओं के बीच की दूरी का आधा भाग होती है। क्लोरीन अणु के लिए सहसंयोजी तथा वांडर वाल त्रिज्याओं को चित्र 4.2 में दर्शाया गया है।
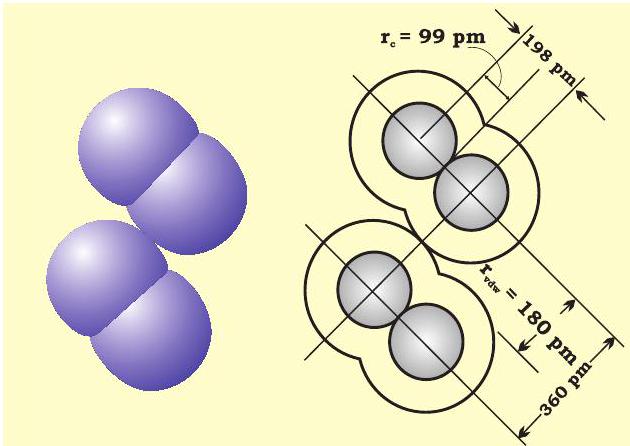
चित्र 4.2: क्लोरीन के अणु हेतु सहसंयोजी एवं वांडरवाल त्रिज्याएं। अंदर के वृत्त क्लोरीन के परमाणु का आकार इंगित करते हैं। ( $r_{\text {vdw }}$ एवं $r_{c}$ क्रमशः वांडरवाल और सहसंयोजी त्रिज्याएं दर्शाते हैं)।
कुछ एकल, द्वि तथा त्रि आबंधों की औसत लंबाइयाँ सारणी 4.2 में दी गई हैं; कुछ सामान्य अणुओं की आबंध लंबाइयाँ सारणी 4.3 में दी गई हैं,
जबकि कुछ सामान्य तत्त्वों की सहसंयोजी त्रिज्याएँ सारणी 4.4 में क्रमबद्ध की गई हैं।
4.3.2 आबंध-कोण
किसी अणु के केंद्रीय परमाणु के आसपास उपस्थित आबंधन इलेक्ट्रॉन युग्म को धारण करने वाले ऑर्बिटलों के बीच बनने वाले कोण को ‘आबंध कोण’ कहते हैं। आबंध कोण को डिग्री के रूप में व्यक्त किया जाता है तथा प्रायोगिक तौर पर स्पेक्ट्रमी विधियों द्वारा ज्ञात किया जाता है। आबंध कोण अणु के केंद्रीय परमाणु के आसपास ऑर्बिटलों के वितरण की जानकारी देता है। अतः इससे हमें अणु/जटिल आयन की आकृति को ज्ञात करने में सहायता मिलती है। जैसे-जल के अणु में $\mathrm{H}-\mathrm{O}-\mathrm{H}$ आबंध कोण को इस प्रकार निरूपित किया जाता है।

4.3.3 आबंध एन्थैल्पी
गैसीय स्थिति में दो परमाणुओं के बीच विशिष्ट आबंधों के एक मोल को तोड़ने के लिए आवश्यक ऊर्जा को ‘आबंध एन्थैल्पी’ कहते हैं। आबंध एन्थैल्पी का मात्रक $\mathrm{kJ} \mathrm{mol}^{-1}$ होता है। उदाहरणार्थ- हाइड्रोजन के अणु में $\mathrm{H}-\mathrm{H}$ आबंध की आबंध एन्थैल्पी $435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ होती है, अर्थात्
$\mathrm{H}_2 (\mathrm{~g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$;
$\Delta_{\mathrm{a}} H^\ominus =435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$
इसी प्रकार, बहुआबंधन वाले परमाणुओं (जैसे- $\mathrm{O} _{2}$ तथा $\mathrm{N} _{2}$ ) के लिए आबंध एन्थैल्पी होगी-
$\mathrm{O} _{2}(\mathrm{O}=\mathrm{O})(\mathrm{g}) \rightarrow \mathrm{O}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=498 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
$\mathrm{N} _{2}(\mathrm{~N} \equiv \mathrm{N})(\mathrm{g}) \rightarrow \mathrm{N}(\mathrm{g})+\mathrm{N}(\mathrm{g}) ;$
$$ \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=946.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
यह तथ्य महत्त्वपूर्ण है कि यदि आबंध विघटन एन्थैल्पी अधिक है, तो आबंध अधिक प्रबल होगा। $\mathrm{HCl}$ जैसे एक विषम नाभिकीय द्विपरमाणुक अणु के लिए
$$ \mathrm{HCl}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{Cl}(\mathrm{g}) ; \Delta_{\mathrm{a}} \mathrm{H}^{\ominus}=431.0 \mathrm{~kJ} \mathrm{~mol}^{-1} $$
बहुपरमाणुक अणुओं में आबंध-सामर्थ्य का निर्धरण अधिक जटिल होता है। उदाहरणार्थ- $\mathrm{H} _{2} \mathrm{O}$ अणु में दो $\mathrm{O}-\mathrm{H}$ आबंधों के विच्छेदन हेतु आवश्यक ऊर्जा समान नहीं है।
सारणी 4.2 कुछ एकल, द्वि तथा त्रि आबंधों की औसत लंबाइयाँ
| आबंध का प्रकार | सहसंयोजी आबंध लंबाई $\mathbf{( p m})$ |
|---|---|
| $\mathrm{O}-\mathrm{H}$ | 96 |
| $\mathrm{C}-\mathrm{H}$ | 107 |
| $\mathrm{~N}-\mathrm{O}$ | 136 |
| $\mathrm{C}-\mathrm{O}$ | 143 |
| $\mathrm{C}-\mathrm{N}$ | 143 |
| $\mathrm{C}-\mathrm{C}$ | 154 |
| $\mathrm{C}=\mathrm{O}$ | 121 |
| $\mathrm{~N}=\mathrm{O}$ | 122 |
| $\mathrm{C}=\mathrm{C}$ | 133 |
| $\mathrm{C}=\mathrm{N}$ | 138 |
| $\mathrm{C} \equiv \mathrm{N}$ | 116 |
| $\mathrm{C} \equiv \mathrm{C}$ | 120 |
सारणी 4.3 कुछ सामान्य अणुओं की आबंध लंबाइयाँ
| अणु | आबंध लंबाई (pm) |
|---|---|
| $\mathrm{H}_{2}(\mathrm{H}-\mathrm{H})$ | 74 |
| $\mathrm{~F}_{2}(\mathrm{~F}-\mathrm{F})$ | 144 |
| $\mathrm{Cl}_{2}(\mathrm{Cl}-\mathrm{Cl})$ | 199 |
| $\mathrm{Br}_{2}(\mathrm{Br}-\mathrm{Br})$ | 228 |
| $\mathrm{I}_{2}(\mathrm{I}-\mathrm{I})$ | 267 |
| $\mathrm{~N}_{2}(\mathrm{~N} \equiv \mathrm{N})$ | 109 |
| $\mathrm{O}_{2}(\mathrm{O}=\mathrm{O})$ | 121 |
| $\mathrm{HF}(\mathrm{H}-\mathrm{F})$ | 92 |
| $\mathrm{HCl}(\mathrm{H}-\mathrm{Cl})$ | 127 |
| $\mathrm{HBr}(\mathrm{H}-\mathrm{Br})$ | 141 |
| $\mathrm{HI}(\mathrm{H}-\mathrm{I})$ | 160 |
सारणी 4.4 सह संयोजी त्रिज्याएँ $\mathbf{r} _{\text {cov }} /(p m)$
| $\mathrm{H}$ | 37 | ||||||
|---|---|---|---|---|---|---|---|
| $\mathrm{C}$ | $77(1)$ | $\mathrm{N}$ | $74(1)$ | $\mathrm{O}$ | $66(1)$ | $\mathrm{F}$ | 64 |
| $67(2)$ | $65(2)$ | $57(2)$ | $\mathrm{Cl}$ | 99 | |||
| $60(3)$ | $55(3)$ | ||||||
| $\mathrm{P}$ | 110 | $\mathrm{~S}$ | $104(1)$ | $\mathrm{Br}$ | 114 | ||
| $95(2)$ | |||||||
| $\mathrm{As}$ | 121 | $\mathrm{Se}$ | 104 | $\mathrm{I}$ | 133 | ||
| $\mathrm{Sb}$ | 141 | $\mathrm{Te}$ | 137 |
- दिए गए मान एकल आबंधों के लिए हैं। अन्य प्रकार के आबंधों को कोष्ठक में दर्शाया गया है। (आवर्ती प्रवृत्ति के लिए एकक 3 भी देखें)
$\mathrm{H}_2 \mathrm{O}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{OH}(\mathrm{g}) ; \Delta_a H_1^\ominus=502 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$\mathrm{OH}(\mathrm{g}) \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{O}(\mathrm{g}) ; \Delta_{\mathrm{a}} H_{2}^{\ominus}=427 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$\Delta \mathrm{H}^{\ominus}$ मानों में अंतर यह दर्शाता है कि परिवर्तित रासायनिक परिस्थिति के कारण द्वितीय $\mathrm{O}-\mathrm{H}$ आबंध में कुछ परिवर्तन आता है। यही कारण है कि $\mathrm{O}-\mathrm{H}$ आबंध की एंथैल्पी विभिन्न अणुओं (जैसे- $\mathrm{C} _{2} \mathrm{H} _{5} \mathrm{OH}$ ऐथेनॉल) तथा जल में भिन्न होती है। इसीलिए बहुपरमाणुक अणुओं में माध्य अथवा औसत आबंध ऊर्जा नामक पद का प्रयोग किया जाता है। इसे प्राप्त करने के लिए कुल आबंध वियोजन एंथैल्पी के मान को विच्छेदित आबंधों की संख्या द्वारा विभाजित किया जाता है।
आबंध की औसत आबंध एंथैल्पी $ = \frac{502+427}{2}$
$$=464.5 \mathrm{~kJ} \mathrm{~mol}^{-1}$$
4.3.4 आबंध कोटि
सहसंयोजी आबंध की लूइस व्याख्या के अनुसार किसी अणु में दो परमाणुओं के मध्य आबंधों की संख्या आबंध कोटि (Bond Order) कहलाती है। उदाहरण के लिए- $\mathrm{H} _{2}$ (जिसमें एक सहभाजित इलेक्ट्रॉन युग्म है), $\mathrm{O} _{2}$ (जिसमें दो सहभाजित इलेक्ट्रॉन युग्म होते हैं) तथा $\mathrm{N} _{2}$ (जिसमें तीन सहभाजित इलेक्ट्रॉन युग्म होते हैं) में आबंध कोटि क्रमशः 1 , 2 तथा 3 है। इसी प्रकार $\mathrm{CO}$ में, जहाँ पर कार्बन तथा ऑक्सीजन के बीच तीन सहभाजित युग्म हैं, आबंध कोटि 3 है। $\mathrm{N} _{2}$ की आबंध कोटि 3 है तथा इसका $\Delta _{\mathrm{a}} \mathrm{H}^{\ominus}$ मान 946 $\mathrm{kJ} \mathrm{mol}^{-1}$ है, जो किसी द्वि-परमाणवीय अणु के लिए सर्वाधिक है।
समइलेक्ट्रॉनी अणुओं तथा आयनों में आबंध कोटि समान होती है। उदाहरण के लिए- $\mathrm{F} _{2}$ तथा $\mathrm{O} _{2}^{2-}$ में आबंध कोटि 1 है।
इसी प्रकार $\mathrm{N} _{2}, \mathrm{CO}$ तथा $\mathrm{NO}^{+}$की आबंध कोटि 3 है। अणुओं के स्थायित्व को समझने के लिए एक उपयोगी सामान्य सहसंबंध यह है कि आबंध-कोटि बढ़ने पर आबंध एंथैल्पी बढ़ती है, जबकि आबंध लंबाई घटती है।
4.3.5 अनुनाद संरचनाएँ
प्रायोगिक निर्धारित प्राचलों (Parameters) के संदर्भ में किसी अणु के निरूपण के लिए एक लूइस-संरचना कई बार पर्याप्त नहीं होती है। उदाहरणार्थ- ओज़ोन अणु को निम्नलिखित संरचनाओं (I व II) द्वारा समान रूप से निरूपित किया जा सकता है-

चित्र 4.3 $\mathrm{O} _{3}$ अणु की अनुनाद संरचनाएँ
[संरचना I व II दो विहित (Canonical) रूप दर्शाते हैं, जबकि संरचना III अनुनाद संकर (Resonance Hybrid) रूप दर्शाती हैं]
दोनों ही संरचनाओं में एक $\mathrm{O}-\mathrm{O}$ एकल आबंध तथा एक $\mathrm{O}=\mathrm{O}$ द्विआबंध उपस्थित हैं। $\mathrm{O}-\mathrm{O}$ एकल तथा द्विआबंधों की सामान्य आबंध लंबाइयाँ क्रमशः $148 \mathrm{pm}$ तथा $121 \mathrm{pm}$ है। प्रयोग द्वारा ज्ञात होता है कि $\mathrm{O} _{3}$ अणु में दोनों $\mathrm{O}-\mathrm{O}$ आबंधों की लंबाई एक समान $128 \mathrm{pm}$ होती है। अत: $\mathrm{O} _{3}$ के अणु में ऑक्सीजन-ऑक्सीजन आबंध, एकल तथा द्विआबंधों का मध्यवर्ती है। अतः उपर्युक्त लूइस संरचनाओं I तथा II में से कोई भी एक संरचना $\mathrm{O} _{3}$ अणु को निरूपित नहीं कर सकती।
$\mathrm{O} _{3}$ जैसे अणुओं की वास्तविक संरचना को स्पष्ट करने के लिए अनुनाद संकल्पना (Resonance Concept) को प्रस्तावित किया गया। इस कल्पना के अनुसार जब किसी अणु को केवल एक लूइस संरचना द्वारा निरूपित नहीं किया जा सके, तो समान ऊर्जा, नाभिकों की समान स्थितियों तथा समान आबंधी एवं अनाबंधी इलेक्ट्रॉन युग्मों वाली कई संरचनाएँ विहित (Canonical) संरचनाओं के रूप में लिखी जाती हैं। इन विहित संरचनाओं का अनुनाद संकर (Resonance Hybrid) अणु की वास्तविक स्थिति को निरूपित करता है। अतः $\mathrm{O} _{3}$ की उपर्युक्त दो संरचनाएँ (I व II) उसकी विहित संरचनाएँ हैं तथा उनका संकरित रूप ( संरचना III) उसकी वास्तविक संरचना को निरूपित करता है।
अनुनाद को दो सिरों वाले तीर द्वारा दर्शाया जाता है। कार्बोनेट आयन तथा कार्बन डाइऑक्साइड अणु अनुनाद संरचना के दो अन्य उदाहरण हैं।
उदाहरण 4.3
$\mathrm{CO} _{3}^{2-}$ आयन की संरचना की व्याख्या अनुनाद द्वारा कीजिए।
हल
कार्बन तथा ऑक्सीजन परमाणुओं के मध्य दो एकल आबंध तथा एक द्वि-आबंध वाली लूइस-संरचना कार्बोनेट आयन की वास्तविक संरचना को निरूपित करने के लिए अपर्याप्त है, क्योंकि इसके अनुसार तीन कार्बनऑक्सीजन आबंधों की लंबाई भिन्न होनी चाहिए। परंतु प्रायोगिक परिणामों के अनुसार कार्बोनेट आयन के तीनों कार्बन-ऑक्सीजन आबंधों की लंबाई समान होती है। अतः कार्बोनेट आयन की वास्तविक संरचना को निम्नलिखित तीन विहित संरचनाओं (I, II, तथा III) के अनुनाद संकर के रूप में दर्शाया जा सकता है-
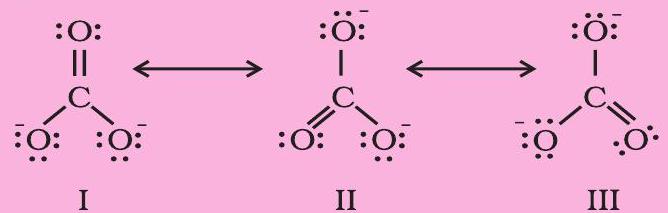
चित्र 4.4 $\mathrm{CO} _{3}^{2-}$ के अणु की संरचना I, II ओर III तीन विहित संरचनाएँ
उदाहरण 4.4
$\mathrm{CO} _{2}$ अणु की संरचना की व्याख्या करें।
हल
$\mathrm{CO} _{2}$ के अणु में कार्बन-ऑक्सीजन आबंध की लंबाई का प्रायोगिक मान $115 \mathrm{pm}$ है। सामान्य कार्बनऑक्सीजन द्वि-आबंध $(\mathrm{C}=\mathrm{O})$ तथा कार्बन-ऑक्सीजन त्रिआबंध $(\mathrm{C} \equiv \mathrm{O})$ की लंबाइयाँ क्रमशः $121 \mathrm{pm}$ तथा $110 \mathrm{pm}$ हैं। $\mathrm{CO} _{2}$ में कार्बन-ऑक्सीजन आबंध की लंबाई $(115 \mathrm{pm}),(\mathrm{C}=\mathrm{O})$ तथा $(\mathrm{C} \equiv \mathrm{O})$ की सामान्य लंबाइयों के बीच होती है। इससे यह स्पष्ट होता है कि $\mathrm{CO} _{2}$ अणु की वास्तविक संरचना को केवल एक लूइस संरचना के आधार पर प्रदर्शित नहीं किया जा सकता। अतः यह आवश्यक हो जाता है कि इसके लिए एक से अधिक लूइस संरचनाएँ लिखी जाएँ तथा $\mathrm{CO} _{2}$ की संरचना को इन विहित संरचनाओं (I, II तथा III) के संकर के रूप में प्रदर्शित किया जाए।

चित्र 4.5 $\mathrm{CO} _{2}$ अणु में अनुनाद संरचनाएँ I, II, तथा III तीन विहित संरचनाओं को दर्शाते हैं।
सामान्य रूप से यह कहा जा सकता है कि
- अनुनाद अणु को स्थायित्व प्रदान करता है, क्योंकि अनुनाद संकर की ऊर्जा किसी भी विहित संरचना की ऊर्जा से कम होती है।
- अनुनाद के कारण आबंधों के लक्षण औसत मान प्राप्त करते हैं।
इस प्रकार $\mathrm{O} _{3}$ अणु में अनुनाद संकर रूप III की ऊर्जा, केनानिकल रूप I तथा II की ऊर्जा के मान से भी कम होती है।
अनुनाद संकल्पना से संबंधित कई भ्राँतिया हैं, जिनका निवारण आवश्यक है। आपको स्मरण रहे कि-
- वास्तव में विहित संरचनाओं का कोई अस्तित्त्व नहीं होता है।
- ऐसा नहीं होता कि अणु कुछ समय के लिए किसी विहित संरचना के रूप में उपस्थित रहता है, जबकि अन्य समय किसी दूसरी विहित संरचना को अपनाता है।
- विहित संरचनाओं में चलावयवों (कीटो तथा इनॉल) के मध्य पाए जाने वाले साम्य जैसा कोई साम्य नहीं होता है।
- वास्तविक रूप में अणु की केवल एक संरचना होती है, जो विहित संरचनाओं की अनुनाद संकर होती है। उसे केवल एक लूइस संरचना द्वारा प्रदर्शित नहीं किया जा सकता है।
4.3.6 आबंध-ध्रुवणता
किसी आबंध का सौ प्रतिशत आयनिक या सहसंयोजी होना एक आदर्श स्थिति है। परंतु वास्तव में कोई भी आबंध या यौगिक पूर्ण रूप से सहसंयोजी या आयनिक नहीं होता है। यहाँ तक कि दो हाइड्रोजन परमाणुओं के बीच बनने वाले सहसंयोजी आबंध की प्रकृति भी आंशिक रूप से आयनिक होती है।
जब सह संयोजी आबंध दो समान परमाणुओं के बीच, ( जैसे- $\mathrm{H} _{2}, \mathrm{O} _{2}, \mathrm{Cl} _{2}, \mathrm{~N} _{2}$ तथा $\mathrm{F} _{2}$ ) बनता है, तब संयोजी इलेक्ट्रॉन युग्म दोनों परमाणुओं द्वारा समान रूप से आकर्षित होता है। इसके परिणामस्वरूप इलेक्ट्रॉन युग्म दो समान नाभिकों के ठीक मध्य में उपस्थित होता है। इस प्रकार प्राप्त आबंध ‘अध्रुवीय सहसंयोजी आबंध’ कहलाता है। इसके विपरित $\mathrm{HF}$ जैसे विषम परमाणुक अणु में दो परमाणुओं के बीच संयोजित इलेक्ट्रॉन युग्म फ्लुओरीन की ओर विस्थापित हो जाता है, क्योंकि फ्लुओरीन की विद्युत् ऋणात्मकता हाइड्रोजन की अपेक्षा अधिक होती है। इस प्रकार निर्मित $\mathrm{H}-\mathrm{F}$ आबंध एक ध्रुवीय सहसंयोजक आबंध है।
ध्रुवण के कारण ऐसे अणु में द्विध्रुव आघूर्ण (Dipole Moment) उत्पन्न हो जाता है। द्विध्रुव को आवेश के मान तथा धनात्मक और ॠणात्मक आवेशों के बीच की दूरी के गुणनफल के रूप में परिभाषित किया जाता है। इसे सामान्यत: ग्रीक शब्द ’ $\mu$ ’ द्वारा दर्शाया जाता है। इसे निम्नलिखित समीकरण द्वारा व्यक्त किया जाता है-
द्विध्रुव आघूर्ण $(\mu)=$ आवेश $(Q) \times$ आवेश पृथक्करण की दूरी $(\mathrm{r})$
द्विध्रुव आघूर्ण को सामान्यतः डिबाए (Debye) मात्रक (D) के रूप में व्यक्त किया जाता है।
$$ 1 \mathrm{D}=3.33564 \times 10^{-30} \mathrm{C} \mathrm{m} $$
जहाँ पर $\mathrm{C}$ कुलॉम तथा $\mathrm{m}$ मीटर है।
इसके अलावा द्विध्रुव आघूर्ण एक सदिश राशि है। परंपरा के अनुसार इसे एक छोटे तीर द्वारा दर्शाया जाता है, जिसका पुच्छल सिरा ऋणात्मक केंद्र पर स्थित होता है तथा अग्र सिरा घनात्मक केंद्र की ओर उन्मुख रहता है। परंतु रसायन में द्विध्रुव आघूर्ण की उपस्थिति अणु की लूइस संरचना के उपर क्रॉस तीर $(\longmapsto)$ द्वारा दर्शाई जाती है। तीर का क्रॉस अणु के घनात्मक सिरे पर और शीर्ष ऋणात्मक सिरे पर होता है। उदाहरण के लिए- $\mathrm{HF}$ में द्विध्रुव आघूर्ण को इस प्रकार दर्शाया जा सकता है-
$$ \stackrel{+}{\mathrm{H} \longrightarrow \ddot{*}}: $$
यह तीर अणु में इलेक्ट्रॉन घनत्व के बदलाव की दिशा बतलाता है। ध्यान दीजिए की क्रॉस तीर की दिशा द्विध्रुव आघूर्ण के सदिश की पारम्परिक दिशा के विपरीत है।
डच रसायनज्ञ पीटर डिबाए को सन् 1936 में उनके $X$-किरणों के विवर्तन तथा द्विध्रुव आघूर्ण से संबंधित उनके कार्य के लिए नोबेल पुरस्कार दिया गया। उनको सम्मानित करने के लिए द्विध्रुव आघूर्ण के मान को डिबाए मात्रक में दिया जाता है।

बहुपरमाणुक अणुओं में द्विध्रुव आघूर्ण केवल आबंधों के अपने द्विध्रुव, जिन्हें ‘आबंध आघूर्ण’ कहा जाता है, पर ही निर्भर नहीं करता, अपितु यह विभिन्न आबंधों की स्थानिक व्यवस्था पर भी निर्भर करता है। ऐसे में द्विध्रुव अणु के विभिन्न आबंधों के द्विध्रुव आघूर्ण अणु के विभिन्न आबंधों के द्विध्रुव आघूर्णो का सदिश-योग (Vector sum) होता है। उदाहरण के लिए- जल के अणु, जिसकी आकृति बंकित होती है, के दो $\mathrm{O}-\mathrm{H}$ आबंध $104.5^{\circ}$ के कोण पर होते हैं। इस अणु में कुल द्विध्रुव आघूर्ण का मान $6.17 \times 10^{-30} \mathrm{Cm}$ [ID = $3.33564 \times$ $10^{-30} \mathrm{Cm}$ होता है, जो दो $\mathrm{O}-\mathrm{H}$ आबंधों के द्विध्रुवों के आघूर्णों के सदिश-योग से प्राप्त होता है।

कुल द्विध्रुव आघूर्ण, $\mu=1.85 \mathrm{D}$
$=1.85 \times 3.33564 \times 10^{-30} \mathrm{C} \mathrm{m}=6.17 \times 10^{-30} \mathrm{C} \mathrm{m}$
$\mathrm{BeF} _{2}$ के लिए द्विध्रुव आघूर्ण का मान शून्य होता है। ऐसा इसलिए होता है कि इस अणु में दो समान आबंध द्विध्रुव विपरीत दिशा में होते हैं तथा एक दूसरे के प्रभाव को समाप्त (Cancel) कर देते हैं।

$\mathrm{BF} _{3}$ जैसे चतुष्क परमाणुवीक अणु में द्विध्रुव आघूर्ण शून्य होता है, यद्यपि इस अणु मे $\mathrm{B}-\mathrm{F}$ आबंध $120^{\circ}$ के कोण पर होते हैं इस अणु में दो आबंध-आघूर्णों के समान तथा विपरीत दिशा में होता है। इसके फलस्वरूप तीनों आबंध-आघूर्णों का कुल सदिश-योग शून्य के बराबर होता है।

$\mathrm{BF} _{3}$ अणु (क) आबंध द्विध्रुव का निरूपण (ख) परिणामी द्विध्रुव आघूर्ण का निरूपण
आइए, $\mathrm{NH} _{3}$ तथा $\mathrm{NF} _{3}$ के अणुओं का एक रोचक उदाहरण लें। दोनों अणुओं की पिरामिडीय आकृति होती है, जिनसे नाइट्रोजन के परमाणु पर एक एकाकी इलेक्ट्रॉन युग्म उपस्थित होता है। हालाँकि फ्लुओरीन, विद्युत् ऋणात्मकता नाइट्रोजन की अपेक्षा अधिक होती है, परंतु $\mathrm{NH} _{3}$ का परिणामी द्विध्रुव आघूर्ण $\left(4.9 \times 10^{-30} \mathrm{Cm}\right) \mathrm{NF} _{3}$ के द्विध्रुव आघूर्ण $\left(0.80 \times 10^{-30} \mathrm{Cm}\right)$ की अपेक्षा अधिक होता है। ऐसा इसलिए है कि $\mathrm{NH} _{3}$ में नाइट्रोजन परमाणु पर उपस्थित एकाकी इलेक्ट्रॉन युग्म का कक्षक द्विध्रुव आघूर्ण तीन $\mathrm{N}-\mathrm{F}$ आबंधों के द्विध्रुव-आघूर्णों के परिणामी द्विध्रुव-आघूर्ण की विपरीत दिशा में होता है। कक्षक द्विध्रूव आघूर्ण एकाकी इलेक्ट्रॉन युग्म के कारण $\mathrm{N}-\mathrm{F}$ आबंध-आघूर्णों के परिणामी द्विध्रुव-आघूर्ण के प्रभाव को कम करता है। इसके फलस्वरूप $\mathrm{NF} _{3}$ के अणु का द्विध्रुव आघूर्ण कम होता है।

कुछ अणुओं के द्विध्रुव आघूर्णों को सारणी 4.5 में दिया गया है।
जिस प्रकार सहसंयोजी आबंध में आंशिक आयनिक लक्षण होता है, उसी प्रकार आयनिक आबंध में भी आंशिक सहसंयोजी लक्षण होता है। आयनिक आबंधों के आंशिक सहसंयोजी लक्षण की विवेचना फाजान्स (Fajans) ने निम्नलिखित नियमों के अनुसार की-
- धनायन के आकार के घटने तथा ऋणायन के आकार के बढ़ने पर आयनिक आबंध के सहसंयोजी लक्षण में वृद्धि होती है।
- धनायन तथा ऋणायन पर आवेश की मात्रा बढ़ने से आयनिक आबंध के सहसंयोजी लक्षण में वृद्धि होती है।
- समान आकार तथा आवेश के धनायनों में से उस धनायन की ध्रुवण-क्षमता अपेक्षाकृत अधिक होती है, जिसका इलेक्ट्रॉनिक विन्यास क्षार तथा क्षारीय मृदा धातुओं के धनायनों के उत्कृष्ट गैस विन्यास $n s^{2} n p^{6}$ की अपेक्षा संक्रमण धातुओं के अनुरूप $(\mathrm{n}-1) d^{\mathrm{n}} n s^{\mathrm{o}}$ होता है।
धनायन, ॠणायन के इलेक्ट्रॉनीय आवेश को आकर्षित कर उसे ध्रुवित करता है। फलतः उनके मध्य आवेश की मात्रा बढ़ती है। यह प्रक्रिया सहसंयोजी आबंध निर्माण के अनुरूप है, जिसमें दो नाभिकों के मध्य इलेक्ट्रॉनीय आवेश घनत्व में वृद्धि होती है। धनायन की ध्रुवण-क्षमता, ॠणायन की ध्रुवता तथा ॠणायन के ध्रुवण की मात्रा इत्यादि वे कारक हैं, जो सम्मिलित रूप से किसी आयनिक आबंध की सहसंयोजकता के प्रतिशत को निर्धारित करते हैं।
4.4 संयोजकता कोश इलेक्ट्रॉन युग्म प्रतिकर्षण सिद्धांत
जैसा पहले बताया गया है, लूइस अवधारणा अणुओं की आकृति की व्याख्या में असमर्थ है। वी. एस. ई. पी. आर. सिद्धांत सहसंयोजी आकृति को समझने के लिए एक सरल कार्यविधि उपलब्ध कराता है। यह विधि सर्वप्रथम सन् 1940 में सिजविक तथा पॉवेल (Sidgwick and Powell) ने परमाणुओं के संयोजकता कोश में उपस्थित इलेक्ट्रॉन युग्मों के बीच प्रतिकर्षण अन्योग्य क्रियाओं के आधार पर प्रतिपादित की थी। इस विधि को नाइहोम तथा गिलेस्पी (Nyholm and Gillespie) ने सन् 1957 में और अधिक विकसित तथा संशोधित किया।
सारणी 4.5 कुछ चयनित अणुओं के द्विध्रुव-आघूर्ण
| अणु का प्रकार (AB) | उदाहरण | द्विध्रुव-आघूर्ण | आकृति |
|---|---|---|---|
| $\mathrm{(AB)}$ | $\mathrm{HF}$ | 1.78 | रैखिक |
| $\mathrm{HCl}$ | 1.07 | रैखिक | |
| $\mathrm{HBr}$ | 0.79 | रैखिक | |
| $\mathrm{HI}$ | 0.38 | रैखिक | |
| $\mathrm{H} _{2}$ | 0 | रैखिक | |
| $\left(\mathbf{A B} _{\mathbf{2}}\right)$ | $\mathrm{H} _{2} \mathrm{O}$ | ||
| $\mathrm{H} _{2} \mathrm{~S}$ | 1.85 | मुड़ा | |
| $\mathrm{CO} _{2}$ | 0.95 | मुड़ा | |
| $\mathrm{NH} _{3}$ | 0 | रैखिक | |
| $\left(\mathbf{A B} _{3}\right)$ | $\mathrm{NF} _{3}$ | 1.47 | त्रिसमनतताक्ष-पिरामिड पिरामिड |
| $\mathrm{BF} _{3}$ | 0.23 | त्रिसमनताक्ष-समतल | |
| $\mathrm{CH} _{4}$ | 0 | चतुष्फलकीय | |
| $\left(\mathbf{A B} _{3}\right)$ | $\mathrm{CHCl} _{3}$ | चतुष्फलकीय | |
| $\mathrm{CCl} _{4}$ | 1.04 | चतुष्फलकीय |
वी. एस. ई. पी. आर. सिद्धांत की मूलभूत धारणाएँ हैं-
- अणु की आकृति, केंद्रीय परमाणु के आसपास उपस्थित संयोजीकोश इलेक्ट्रॉन युग्मों (संयोजित अथवा असंयोजित) की संख्या पर निर्भर करती है।
- केंद्रीय परमाणु के संयोजकता कोश में उपस्थित इलेक्ट्रॉन युग्म एक-दूसरे को प्रतिकर्षित करते हैं, क्योंकि उनके इलेक्ट्रॉन अभ्र (Electron Cloud) पर ऋणात्मक आवेश होता है।
- ये इलेक्ट्रॉन युग्म त्रिविम में उन स्थितियों में अवस्थित होने का प्रयत्न करते हैं, जिसके फलस्वरूप उनमें प्रतिकर्षण कम से कम हो। इस स्थिति में उनके मध्य अधिकतम दूरी होती है।
- संयोजकता-कोश को एक गोले के रूप में माना जाता है तथा इलेक्ट्रॉन युग्म गोलीय (Spherical) सतह पर एक दूसरे से अधिकतम दूरी पर स्थित होते हैं।
- बहुआबंध को एक एकल इलेक्ट्रॉन युग्म के रूप में तथा इस बहुआबंध के दो या तीन इलेक्ट्रॉन युग्मों को एकल सुपर युग्म समझा जाता है।
- यदि अणु को दो या अधिक अनुनाद संरचनाओं द्वारा दर्शाया जा सके, तो इस स्थिति में वी. एस. ई. पी. आर मॉडल ऐसी प्रत्येक संरचना पर लाग होता है।
इलेक्ट्रॉन युग्मों के बीच प्रतिकर्षण अन्योन्य क्रियाएँ निम्नलिखित क्रम में घटती हैं-
एकाकी युग्म (lp) - एकाकी युग्म (lp) > एकाकी युग्म (lp) - आबंधी युग्म (bp) > आबंधी युग्म (bp) - आबंधी युग्म (bp)
नाईहोम तथा गिलेस्पी ने इलेक्ट्रॉनों के एकाकी युग्मों तथा आबंधी युग्मों के महत्त्वपूर्ण अंतरों की व्याख्या करते हुए वी. एस. ई. पी. आर. मॉडल में सुधार किया। एकाकी इलेक्ट्रॉन युग्म केंद्रीय परमाणु पर स्थानगत (Localised) होते हैं, जबकि प्रत्येक आबंधी युग्म दो परमणुओं के बीच सहभाजित होता है। अतः किसी अणु में आबंधी इलेक्ट्रॉन युग्म की अपेक्षा एकाकी युग्म अधिक स्थान घेरते हैं। इसके फलस्वरूप एकाकी इलेक्ट्रॉन युग्मों के बीच एकाकी युग्म-आबंधी युग्म तथा आबंधी युग्मआबंधी युग्म की अपेक्षा अधिक प्रतिकषर्ण होता है। इन प्रतिकर्षणप्रभावों के कारण अणु की संभावित आकृति में भिन्नता होती है तथा अणु के आबंध कोणों में भी अंतर आ जाता है।
वी. एस. ई. पी. आर. मॉडल की सहायता से अणुओं की ज्यामितीय आकृतियों का पूर्वानुमान लगाने के लिए अणुओं को दो श्रेणियों में बाँटा जाता है- (i) वे अणु, जिनके केंद्रीय परमाणु पर कोई भी एकाकी युग्म उपस्थित नहीं होता है। (ii) वे अणु, जिनके केंद्रीय परमाणु पर एक या एक से अधिक एकाकी युग्म उपस्थित होते हैं।
सारणी 4.6 में एकाकी युग्मरहित केंद्रीय परमाणु $\mathrm{A}$ के चारों ओर इलेक्ट्रॉन युग्मों की व्यवस्था तथा $\mathrm{AB}$ प्रकार के कुछ अणुओं अथवा आयनों की ज्यामितियाँ दर्शाई गई हैं। सारणी 4.7 में कुछ उन सरल अणुओं तथा आयनों की ज्यामिति दी गई है, जिनके केंद्रीय परमाणु पर एक या एक से अधिक एकाकी युग्म उपस्थित होते हैं। सारणी 4.8 अणुओं की ज्यामिति में विरूपण (Distortion) की व्याख्या करती है।
जैसा सारणी 4.6 में दर्शाया गया है, $\mathrm{AB} _{2}, \mathrm{AB} _{3}, \mathrm{AB} _{4}$, $\mathrm{AB} _{5}$, तथा $\mathrm{AB} _{6}$ प्रकार के यौगिकों के अणुओं में केंद्रीय परमाणु $\mathrm{A}$ की चारों ओर इलेक्ट्रॉन युग्मों तथा $\mathrm{B}$ परमाणुओं की व्यवस्था क्रमशः इस प्रकार है- रैखिक, त्रिकोणीय समतल, चतुष्फलकीय, त्रिफलकीय-द्विपिरामिडी तथा अष्टफलकीय। इस प्रकार की ज्यामितियाँ $\mathrm{BF} _{3}\left(\mathrm{AB} _{3}\right), \mathrm{CH} _{4}\left(\mathrm{AB} _{4}\right)$ तथा $\mathrm{PCl} _{5}\left(\mathrm{AB} _{5}\right)$ अणुओं द्वारा दर्शाई जाती हैं। इन अणुओं की ज्यामितियों को गेंद-डंडी (Ball-stick) मॉडलों द्वारा नीचे प्रदर्शित किया गया है-
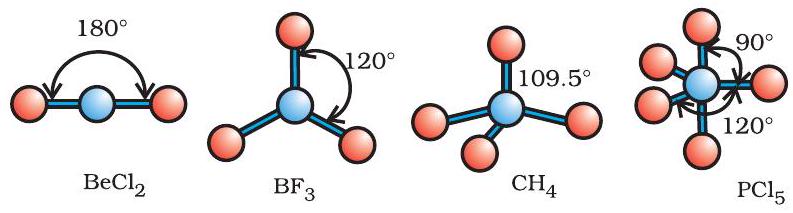
चित्र 4.8 बिना एकाकी युग्म वाले केंद्रीय परमाणु युक्त अणुओं की आकृतियाँ
वी. एस. ई. पी. आर. मॉडल की सहायता से अनेक अणुओं, विशेष रूप से $p$-ब्लाक के तत्त्वों द्वारा निर्मित यौगिकों की ज्यामितियों का पूर्वानुमान सही रूप से लगाया जा सकता है। यहाँ तक कि संभावित संरचनाओं में ऊर्जा का अंतर कम होने पर भी इसके द्वारा वास्तविक संरचना का पूर्वानुमान सफलतापूर्वक लगाया जा सकता है। आण्विक ज्यामिति पर ‘इलेक्ट्रॉन युग्म’ प्रतिकर्षण के प्रभाव के विषय में वी. एस. ई. पी. आर. मॉडल का सैद्धांतिक आधार स्पष्ट नहीं है। इस विषय में अभी भी शंकाएँ उठाई जाती हैं फलतः यह विवेचन का विषय बना हुआ है।
सारणी 4.6 एकाकी युग्मरहित केंद्रित परमाणु युक्त अणुओं की ज्यामिति
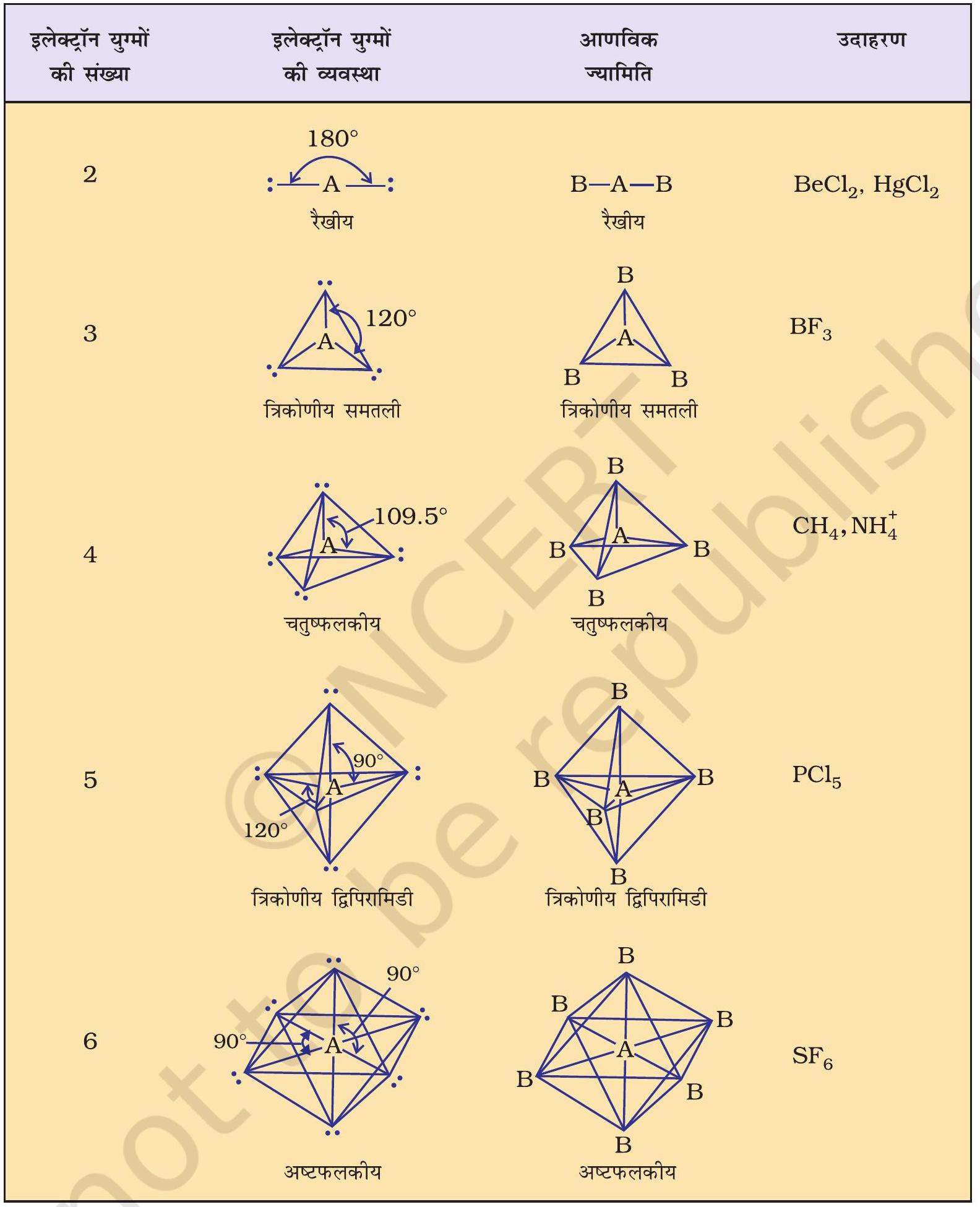
सारणी 4.7 कुछ सरल अणुओं/आयनों की आकृतियाँ (ज्यामिति), जिनके केंद्रीय परमाणु पर एक या एक से अधिक एकाकी इलेक्ट्रॉन युग्म उपस्थित हैं।
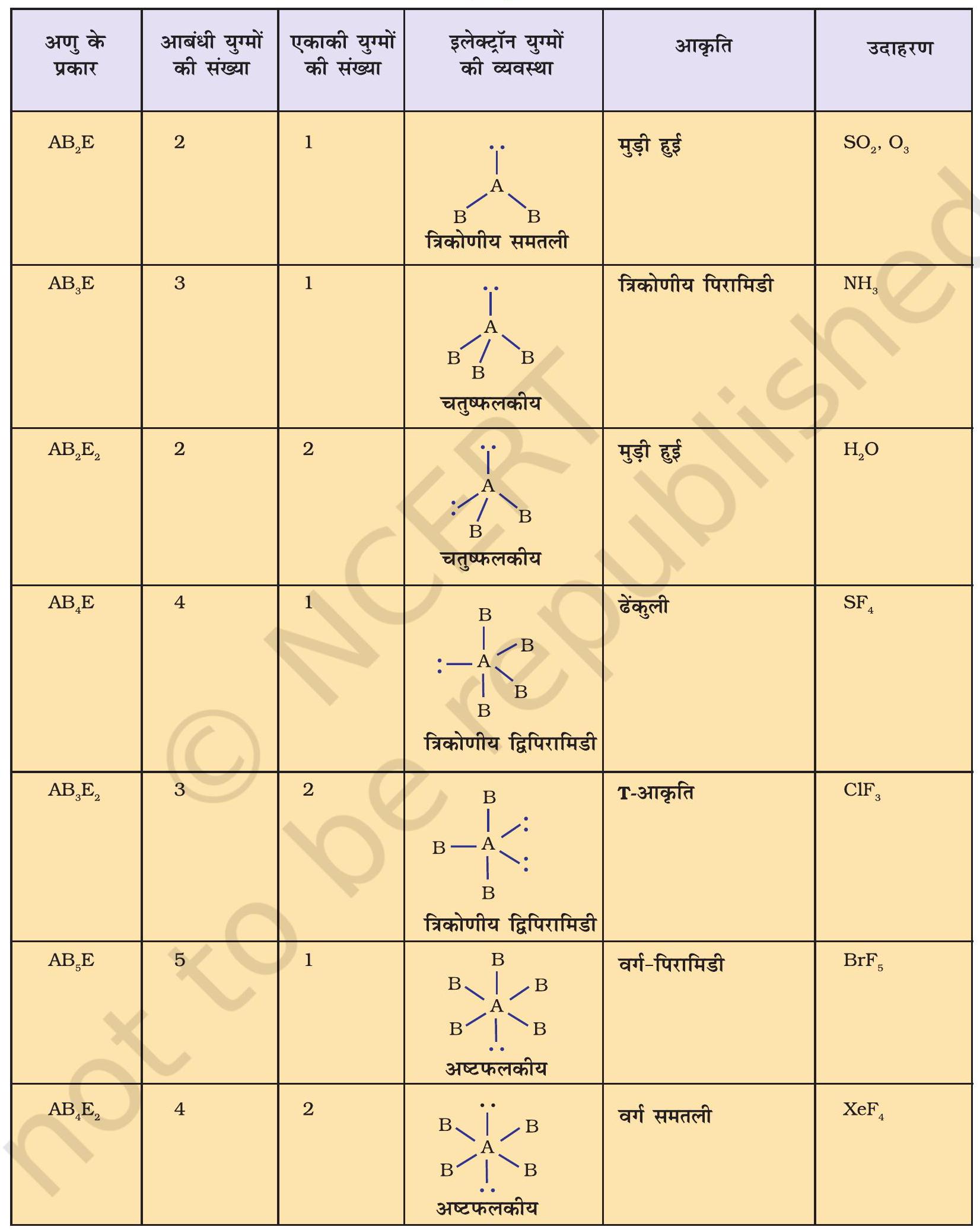
सारणी 4.8 आबंधी-युग्म तथा एकाकी युग्म वाले कुछ अणुओं की आकृति
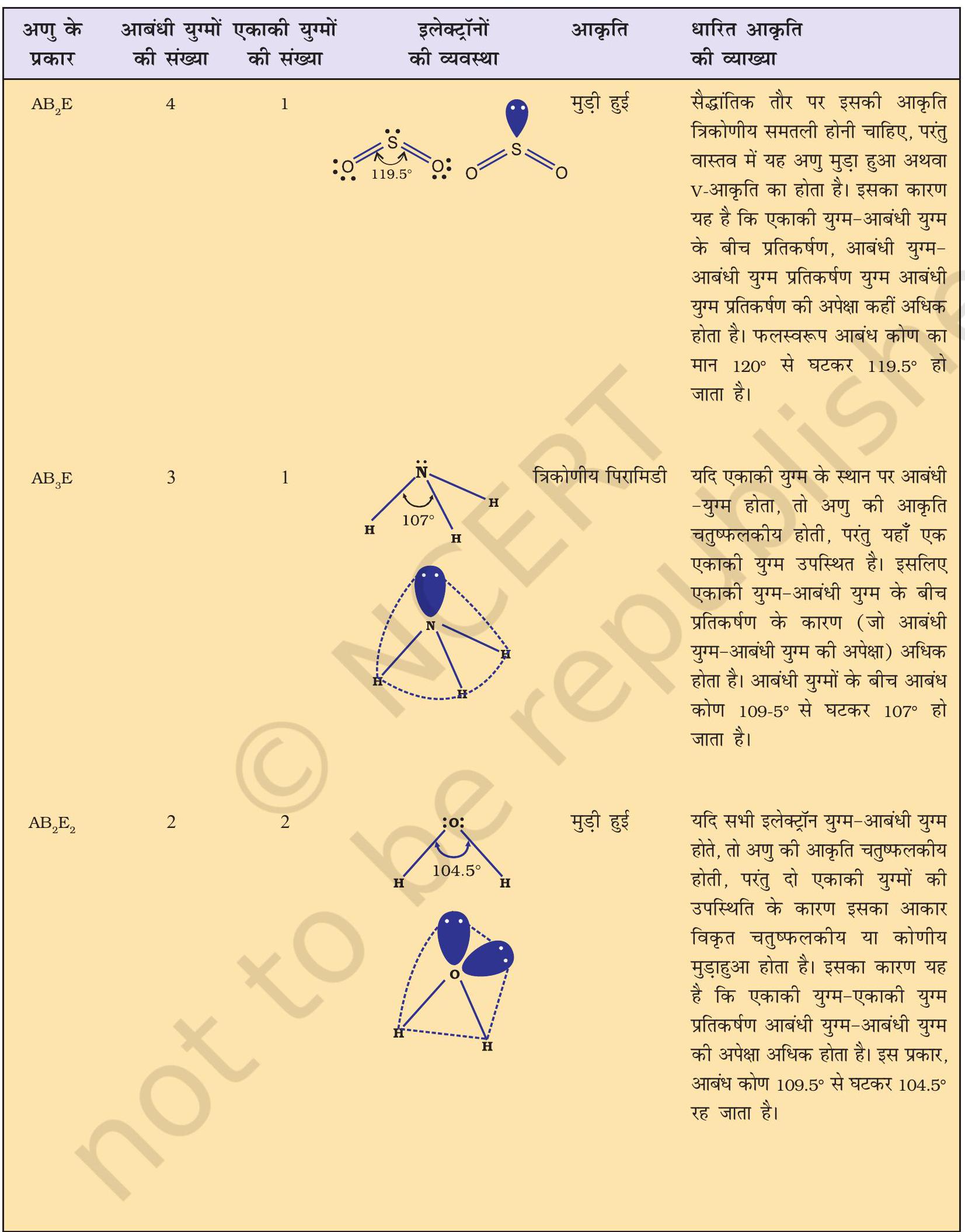
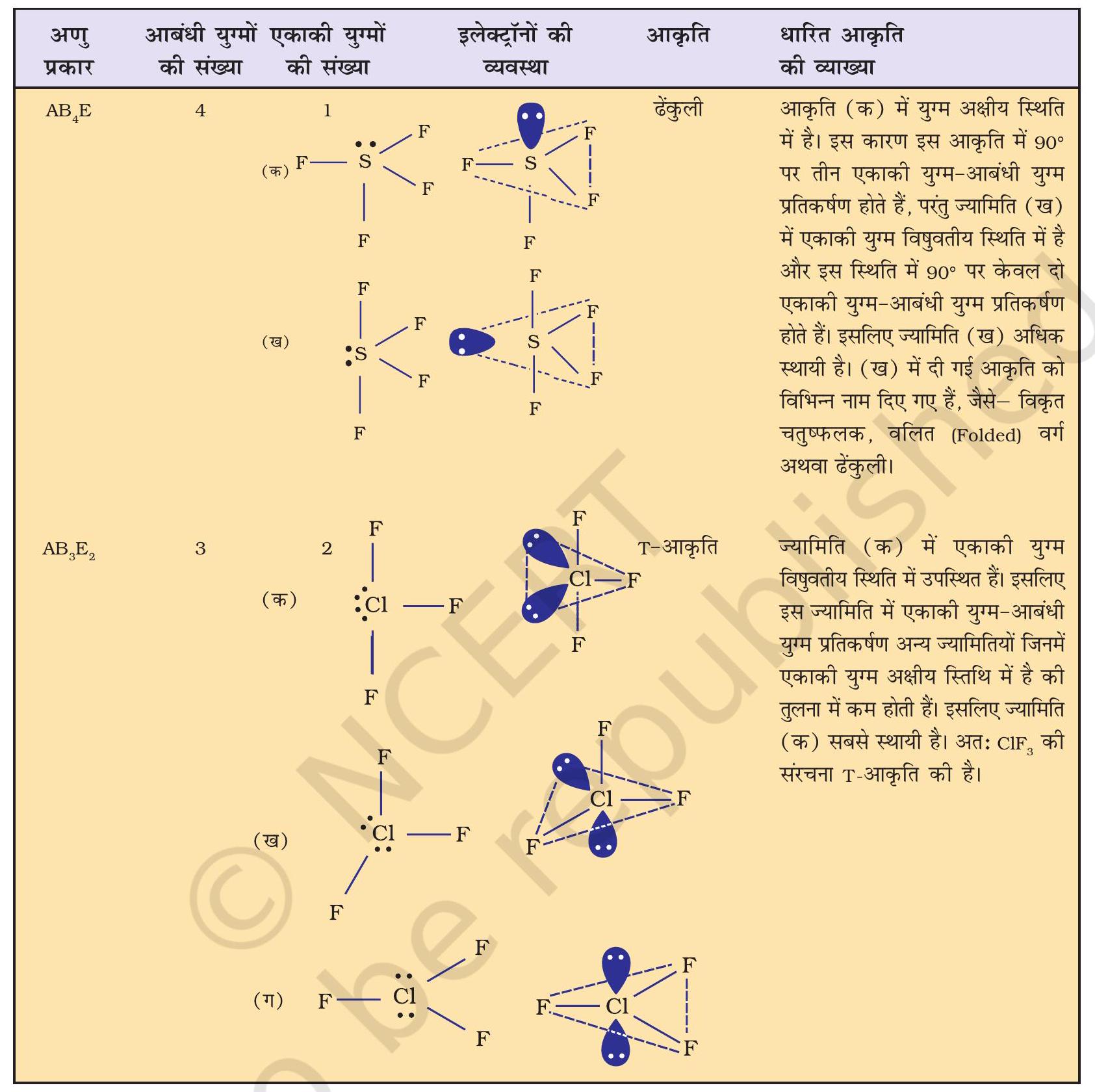
4.5 संयोजकता आबंध सिद्धांत
जैसा आप जानते हैं लूइस अवधारणा से अणुओं की संरचनाओं को लिखने में सहायता मिलती है, परंतु रासायनिक आबंध बनने की व्याख्या करने में यह असमर्थ है। उक्त अवधारणा यह भी स्पष्ट नहीं करती कि अणुओं की आबंध वियोजन ऊर्जाएँ (Bond Dissociation Energies) तथा आबंध लंबाइयाँ जैसे - $\mathrm{H} _{2}\left(435.8 \mathrm{~kJ} \mathrm{~mol}^{-1}, 74 \mathrm{pm}\right)$ और $\mathrm{F} _{2}(150.6 \mathrm{~kJ}$ $\left.\mathrm{mol}^{-1}, 144 \mathrm{pm}\right)$ भिन्न क्यों हैं, जबकि दोनों ही अणुओं में संबंधित परमाणुओं के बीच एक इलेक्ट्रॉन युग्म के सहभाजन के फलस्वरूप एकल सहसंयोजी आबंध बनता है। यह मॉडल बहुपरमाणुक अणुओं की आकृतियों की विभिन्नता पर भी प्रकाश नहीं डालता।
इसी प्रकार वी. एस. ई. पी. आर. सिद्धांत सरल अणुओं की आकृति के बारे में जानकारी देता है, परंतु यह उनकी व्याख्या नहीं कर सकता था। इसका उपयोग भी सीमित है। इन कमियों को दूर करने के लिए दो महत्त्वपूर्ण सिद्धांतों का प्रतिपादन किया गया है, जो क्वांटम यांत्रिकी (Quantum Mechanical) सिद्धांत पर आधारित हैं। ये सिद्धांत हैसंयोजकता आबंध सिद्धांत तथा अणु-कक्षक सिद्धांत (Molecular Orbital Theory)।
संयोजकता आबंध सिद्धांत को सर्वप्रथम हाइटलर तथा लंडन (Heitler and London) ने सन् 1927 में प्रस्तुत किया था, जिसका विकास पॉलिंग (Pauling) तथा अन्य वैज्ञानिकों ने बाद में किया। इस सिद्धांत का विवेचन परमाणु कक्षकों, तत्त्वों के इलेक्ट्रॉनिक विन्यासों (इकाई 2), परमाणु कक्षकों के अतिव्यापन और संकरण तथा विचरण (Variation) एवं अध्यारोपण (Superposition) के सिद्धांतों के ज्ञान पर आधारित है। इन सभी पहलुओं के परिपेक्ष्य में संयोजकता आबंध सिद्धांत का गूढ़ विवेचन इस पुस्तक की विषय-वस्तु से बाहर है। अत: इस सिद्धांत का वर्णन केवल गुणात्मक दृष्टि से तथा गणित का उपयोग किए बिना ही किया जाएगा। आइए, प्रारंभ में सरलतम अणु, $\left(\mathrm{H} _{2}\right)$ के विरचन पर विचार करते हैं।
मान लीजिए कि हाइड्रोजन के दो परमाणु $\mathrm{A}$ व $\mathrm{B}$, जिनके नाभिक क्रमशः $N_{A}$ व $N_{B}$ हैं तथा उनमें उपस्थित इलेक्ट्रॉनों को $\mathrm{e} _{\mathrm{A}}$ और $\mathrm{e} _{\mathrm{B}}$ द्वारा दर्शाया गया है, एक दूसरे की ओर बढ़ते हैं। जब ये दो परमाणु एक दूसरे से अत्यधिक दूरी पर होते हैं, तब उनके बीच कोई अन्योन्य क्रिया नहीं होती। ज्यों-ज्यों दोनों परमाणु एक-दूसरे के पास आते जाते हैं, त्यों-त्यों उनके बीच आकर्षण तथा प्रतिकर्षण बल उत्पन्न होते जाते हैं।
आकर्षण बल निम्नलिखित में उत्पन्न होते हैं-
(i) एक परमाणु के नाभिक तथा उसके इलेक्ट्रॉनों के बीच $\mathrm{N} _{\mathrm{A}}-\mathrm{e} _{\mathrm{A}}, \mathrm{N} _{\mathrm{B}}-\mathrm{e} _{\mathrm{B}}$
(ii) एक परमाणु के नाभिक तथा दूसरे परमाणु के इलेक्ट्रॉनों के बीच $\mathrm{N} _{\mathrm{A}}-\mathrm{e} _{\mathrm{B}}, \mathrm{N} _{\mathrm{B}}-\mathrm{e} _{\mathrm{A}}$
इसी प्रकार प्रतिकर्षण बल निम्नलिखित में उत्पन्न होते हैं-
(i) दो परमाणुओं के इलेक्ट्रॉनों के बीच $e_{A}-e_{B}$ तथा
(ii) दो परमाणुओं के नाभिकों के बीच $\mathrm{N} _{\mathrm{A}}-\mathrm{N} _{\mathrm{B}}$ ।
आकर्षण बल दोनों परमाणुओं को एक-दूसरे के पास लाते हैं, जबकि प्रतिकर्षण बल उन्हें दूर करने का प्रयास करते हैं (चित्र 4.7)।

चित्र 4.7 $\mathrm{H} _{2}$ अणु के विरचन में आकर्षण तथा प्रतिकर्षण बल
प्रायोगिक तौर पर यह पाया गया है कि नए आकर्षण बलों का मान नए प्रतिकर्षण बलों के मान से अधिक होता है। इसके परिणाम- स्वरूप दोनों परमाणु एक-दूसरे के करीब आते हैं तथा उनकी स्थितिज ऊर्जा कम हो जाती है। अंततः ऐसी स्थिति है, नेट आकर्षण बल तथा प्रतिकर्षण बल के बराबर हो जाता है और निकाय की ऊर्जा न्यून स्तर पर पहुँच जाती है। इस अवस्था में हाइड्रोजन के परमाणु ‘आबंधित’ कहलाते हैं और एक स्थायी अणु बनाते हैं, जिसकी आबंध लंबाई $74 \mathrm{pm}$ होती है।
चूँकि हाइड्रोजन के दो परमाणुओं के बीच आबंध बनने पर ऊर्जा मुक्त होती है, इसलिए हाइड्रोजन अणु दो पृथक् परमाणुओं की अपेक्षा अधिक स्थायी होता है। इस प्रकार मुक्त ऊर्जा ‘आबंध एंथैल्पी’ कहलाती है। यह चित्र 4.8 में दिए गए आरेख में न्यूनतम के संगत होती है। विलोमतः $\mathrm{H} _{2}$ के एक मोल अणुओं के वियोजन के लिए $435.8 \mathrm{~kJ}$ ऊर्जा की आवश्यकता होती है।
$\mathrm{H} _{2}(\mathrm{~g})+435.8 \mathrm{~kJ} \mathrm{~mol}^{-1} \rightarrow \mathrm{H}(\mathrm{g})+\mathrm{H}(\mathrm{g})$
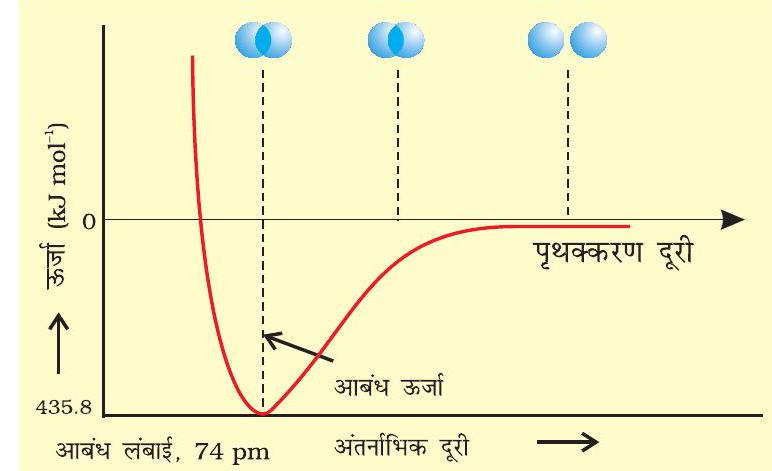
चित्र 4.8: $\mathrm{H} _{2}$ अणु के विरचन के लिए $\mathrm{H}$ परमाणुओं के बीच अंतरानाभिक दूरी की सापेक्ष स्थितिज ऊर्जा का आरेख, आरेख में न्यूनतम ऊर्जा स्थिति $\mathrm{H} _{2}$ की सर्वाधिक स्थायी अवस्था दर्शाती है।
4.5.1 कक्षक अतिव्यापन अवधारणा
हाइड्रोजन अणु के विरचन में इस अवस्था में न्यूनतम ऊर्जा अवस्था प्राप्त होती है। इस अवस्था में दो परमाणु इतने करीब हो जाते हैं कि उनके परमाणु-कक्षक आंशिक रूप से अंतरभेदन ‘परमाणु-कक्षक अतिव्यापन’ कहलाता है। इसके परिणामस्वरूप इलेक्ट्रॉन संयुग्मित होते हैं। अतिव्यापन की सीमा सहसंयोजी आबंध की प्रबलता को निर्धारित करती है। सामान्यतः अधिक अतिव्यापन दो परमाणुओं के बीच प्रबल आबंध बनाने से संबंधित है। इस प्रकार, कक्षक अतिव्यापन अवधारणा के अनुसार दो परमाणुओं के बीच सहसंयोजी आबंध का बनना संयोजकता कक्ष में उपस्थित विपरीत चक्रण (Spin) वाले इलेक्ट्रॉनों के संयुग्मन के परिणामस्वरूप होता है।
4.5.2 आबंधों के दिशात्मक गुणधर्म
जैसा आप जानते हैं, सहसंयोजी आबंध परमाणु कक्षकों के अतिव्यापन से बनते हैं। उदाहरण के लिए- हाइड्रोजन का अणु बनने में इसके दो परमाणुओं के संयोजन में उनके $1 \mathrm{~s}$ कक्षकों का अतिव्यापन होता है।
$\mathrm{CH} _{4}, \mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ जैसे बहुपरमाणुक अणुओं में आबंध बनने के साथ-साथ अणु की ज्यामिति भी महत्त्वपूर्ण होती है। उदाहरण के लिए- $\mathrm{CH} _{4}$ के अणु की आकृति चतुष्फलकीय क्यों होती है और $\mathrm{HCH}$ आबंध कोण का मान $109^{\circ} 28^{\prime}$ क्यों होता है? अथवा $\mathrm{NH} _{3}$ अणु की आकृति पिरामिडी क्यों होती है?
‘संयोजकता आबंध सिद्धांत’ के आधार पर $\mathrm{CH} _{4}, \mathrm{NH} _{3}$ $\mathrm{H} _{2} \mathrm{O}$ आदि बहुपरमाणुक अणुओं की आकृति, उनमें आबंध विरचन तथा उनके दिशात्मक गुणों को परमाणु कक्षकों के संकरण तथा अतिव्यापन की सहायता से स्पष्ट किया जा सकता है।
4.5.3 परमाणु कक्षकों का अतिव्यापन
जब दो परमाणु आबंध विचरण के लिए पास आते हैं, तब उनके कक्षकों का अतिव्यापन धनात्मक, ॠणात्मक या शून्य हो सकता है। यह ऑर्बिटल तरंग फलन के आयाम (amplitude) की दिक्स्थान (स्पेस) में दिशा और चिह्न (फ़ेज़) पर निर्भर करता है (चित्र 4.9)। सीमा- सतह आरेखों पर दर्शाए गए धनात्मक और ऋणात्मक चिह्न तरंग फलन का चि्न (फ़ेज़) बतलाते हैं। इनका आवेश से कोई संबंध नहीं होता। आबंध बनाने के लिए ऑर्बिटलों का चिह्न (फ़ेज़) और अभिविन्यास एक समान होना चाहिए। इसे धनात्मक अतिव्यापन कहते हैं। $s$ तथा $p$ परमाणु कक्षकों के धनात्मक, ऋणात्मक या शून्य अतिव्यापन की विभिन्न अवस्थाएँ, चित्र 4.9 में दर्शाई गई हैं।
सहसंयोजी आबंध के विरचन के मुख्य कारक के रूप में अतिव्यापन की कसौटी समनाभिकीय विषमनाभिकीय द्विपरमाणुक अणुओं तथा बहुपरमाणुक अणुओं पर समान रूप से लागू होता है। हम जानते हैं कि $\mathrm{CH} _{4}, \mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ अणुओं की आकृति क्रमशः चतुष्फलकीय, पिरामिडी तथा मुड़ी हुई होती है। अतः संयोजकता आबंध सिद्धांत का उपयोग करके यह जानना रोचक होगा कि क्या इन ज्यामितीय आकृतियों को कक्षक-अतिव्यापन के आधार पर स्पष्ट किया जा सकता है।
आइए, सर्वप्रथम हम मेथेन $\left(\mathrm{CH} _{4}\right)$ के अणु पर विचार करते हैं। तलस्थ अवस्था (Ground State) में कार्बन का इलेक्ट्रॉन विन्यास [He] $2 s^{2} 2 p^{2}$ है, जो उत्तेजित अवस्था में [He] $2 s^{1} 2 p _{\mathrm{x}}{ }^{1} 2 p _{\mathrm{y}}{ }^{1} 2 p _{\mathrm{z}}{ }^{1}$ हो जाता है। इसके उत्तेजन के लिए आवश्यक ऊर्जा की पूर्ति संकरित कक्षकों तथा हाइड्रोजन के बीच अतिव्यापन के फलस्वरूप मुक्त अतिरिक्त ऊर्जा से होती है।

चित्र 4.9 $\mathrm{~s}$ तथा $p$ परमाणु कक्षकों के धनात्मक, ॠणात्मक तथा शून्य अतिव्यापन
कार्बन के चार परमाणु कक्षक, जिनमें से प्रत्येक में एक अयुग्मित इलेक्ट्रॉन उपस्थित होता है, चार हाइड्रोजन परमाणुओं के एक-एक इलेक्ट्रॉनयुक्त $1 \mathrm{~s}$ कक्षकों के साथ अतिव्यापन कर सकते हैं। परंतु इस प्रकार निर्मित चार $\mathrm{C}-\mathrm{H}$ आबंध समरूप नहीं होंगे। कार्बन के तीन $2 p$ कक्षकों के मध्य $90^{\circ}$ का कोण होने के कारण इन कक्षकों द्वारा निर्मित आबंधों के बीच $\mathrm{HCH}$ कोण का मान भी $90^{\circ}$ होगा, अर्थात् तीन $\mathrm{C}-\mathrm{H}$ आबंध एक-दूसरे के साथ $90^{\circ}$ का कोण बनाएंगे। कार्बन का $2 s$ कक्षक तथा $\mathrm{H}$ का $1 \mathrm{~s}$ कक्षक गोलीय सममित का होने के कारण किसी भी दिशा में अतिव्यापन कर सकता है। अतः चौथे $\mathrm{C}-\mathrm{H}$ आबंध की दिशा अनिश्चित होगी। यह निरूपण $\mathrm{CH} _{4}$ की वास्तविक आकृति से मेल नहीं खाता है, जिसमें चारों $\mathrm{HCH}$ कोण चतुष्फलकीय होते हैं तथा प्रत्येक का मान $109.5^{\circ}$ होता है। इससे स्पष्ट होता है कि केवल कक्षकों के अतिव्यापन के आधार पर $\mathrm{CH} _{4}$ के आबंधों के दिशात्मक गुणों को स्पष्ट नहीं किया जा सकता है। इन्हीं तर्कों के आधार पर $\mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ अणुओं में $\mathrm{HNH}$ तथा $\mathrm{HOH}$ कोणों के मान $90^{\circ}$ होने चाहिए, जो वास्तविक तथ्यों के अनुरूप नहीं है। $\mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ में वास्तविक आबंध कोण क्रमशः $107^{\circ}$ तथा $104.5^{\circ}$ होते हैं।
4.5.4 अतिव्यापन के प्रकार तथा सहसंयोजी आबंध की प्रकृति
कक्षकों के अतिव्यापन के प्रकार के आधार पर सहसंयोजी आबंध के दो प्रकार होते हैं-
(i) सिग्म ( $\sigma)$ आबंध तथा (ii) पाई ( $\pi$ ) आबंध
(i) सिग्मा ( $\sigma$ ) आबंध - इस प्रकार का सहसंयोजी आबंध, आबंधी कक्षकों के अंतर्नाभिकीय अक्ष पर सिरेवार (Head on) अतिव्यापन या अक्षीय (axial) अतिव्यापन कहते हैं। इस प्रकार का आबंध, परमाणु कक्षकों के निम्नलिखित में से किसी एक प्रकार के संयोजन द्वारा प्राप्त किए जा सकते हैं-
- s-s अतिव्यापन- इस प्रकार के संयोजन में दो अर्ध-भृत (Half Filled) $s$-कक्षक अंतर्नाभिकीय अक्ष पर अतिव्यापन करते हैं, जैसा नीचे दिखाया गया है-

- $\boldsymbol{s}$ - $\boldsymbol{p}$ अतिव्यापन- इस प्रकार का अतिव्यापन एक परमाणु की अर्ध-भृत $s$-कक्षक तथा दूसरे परमाणु का अर्ध-भृत $p$-कक्षक के बीच होता है।

- $\boldsymbol{p}-\boldsymbol{p}$ अतिव्यापन- इस प्रकार का अतिव्यापन दो परमाणुओं के अर्ध-भृत $p$-कक्षकों के बीच होता है।

(ii) पाई $(\pi$ आबंध $)$ - पाई आबंध के बनने के आण्विक कक्षक इस प्रकार अतिव्यापन करते हैं कि उनके अक्ष एक दूसरे के समांतर तथा अंतर्नाभिकीय कक्ष से लंबवत होते हैं। इस प्रकार पार्श्व अतिव्यापन के फलस्वरूप निर्मित कक्षक में परमाणुओं के तल के ऊपर तथा नीचे दो प्लेटनुमा आवेशित अभ्र होते हैं।

4.5.5 सिग्मा तथा पाई आबंधों की प्रबलता
मूलतः आबंध की प्रबलता अतिव्यापन की सीमा पर निर्भर करती है। सिग्मा आबंध में कक्षकों का अतिव्यापन अधिक होता है। इसलिए सिग्मा आबंध, पाई आबंध (जिसमें कम अतिव्यापन होता है) की तुलना में अधिक प्रबल होता है। इसके अलावा यह जानना भी महत्त्वपूर्ण है कि दो परमाणुओं के बीच पाई आबंध कभी अकेला नहीं पाया जाता है। यह सदैव सिग्मा आबंध के साथ ही होता है। यह सदैव उन अणुओं में पाया जाता है, जिनमें द्विआबंध या त्रिआबंध उपस्थित होते हैं।
4.6 संकरण
$\mathrm{CH} _{4}, \mathrm{NH} _{3}, \mathrm{H} _{2} \mathrm{O}$ जैसे बहुपरमाणुक अणुओं की विशिष्ट ज्यामितीय आकृतियों को स्पष्ट करने के लिए पॉलिंग ने परमाणु कक्षकों के संकरण का सिद्धांत प्रस्तावित किया। पॉलिंग के अनुसार परमाणु कक्षक संयोजित होकर समतुल्य कक्षकों का समूह बनाते हैं। इन कक्षकों को संकर कक्षक कहते हैं। आबंध विरचन में परमाणु शुद्ध कक्षकों के स्थान पर संकरित कक्षकों का प्रयोग करते हैं। इस परिघटना को हम संकरण कहते हैं। लगभग समान ऊर्जा वाले कक्षकों के आपस में मिलकर ऊर्जा के पुनर्वितरण द्वारा समान ऊर्जा तथा आकार वाले कक्षकों को बनाने की प्रक्रिया को संकरण कहते हैं। उदाहरण के लिएकार्बन का एक $2 s$ कक्षक तथा तीन $2 p$ कक्षक संकरण द्वारा चार नए $s p^{3}$ संकर कक्षक बनाते हैं।
संकरण के महत्त्वपूर्ण लक्षण- संकरण के मुख्य लक्षण इस प्रकार हैं-
1. संकर कक्षकों की संख्या संकरण की प्रक्रिया में भाग लेने वाले कक्षकों की संख्या के बराबर होती है।
2. संकर कक्षक सदैव समान ऊर्जा तथा आकार के होते हैं।
3. संकर कक्षक स्थायी आबंध बनाने में शुद्ध कक्षकों की अपेक्षा अधिक सक्षम होते हैं।
4. संकर कक्षक स्थायी व्यवस्था पाने के लिए त्रिविम में विशिष्ट दिशाओं में निर्देशित होते हैं। इसलिए संकरण का प्रकार अणु की ज्यामिति दर्शाता है।
संकरण की मुख्य परिस्थितियाँ
(i) परमाणु के संयोजकता कक्ष के कक्षक संकरित होते हैं।
(ii) संकरित होने वाले कक्षकों की ऊर्जा लगभग समान होनी चाहिए।
(iii) संकरण के लिए इलेक्ट्रॉन का उत्तेजन आवश्यक नहीं है।
(iv) यह आवश्यक नहीं है कि केवल अर्ध-भृत कक्षक ही संकरण में भाग लें। कभी-कभी संयोजकता कक्ष के पूर्ण-भृत तथा खाली कक्षक भी संकरित हो सकते हैं।
4.6.1 संकरण के प्रकार
$s, p$ तथा $d$ कक्षकों के संकरण निम्नलिखित प्रकार के होते हैं-
(I) $\boldsymbol{s p}$ संकरण इस प्रकार के संकरण में एक $s$ तथा एक $p$ कक्षक संकरित होकर दो समान $s p$ संकर कक्षकों का निर्माण करते हैं। $z$-अक्ष पर संकरण कक्षकों को पाने हेतु, $s p$ संकरण के लिए $s$ तथा $p_{z}$ कक्षक उपयुक्त होते हैं। प्रत्येक $s p$ संकर कक्षक में $50 % s$-लक्षण तथा $50 % p$-लक्षण होता है। यदि किसी अणु में केंद्रीय परमाणु के संयोजकता कक्ष के कक्षक $s p$ संकरित होते हैं तथा दो परमाणुओं से आबंध बनाते हैं, तो अणु की रैखिक ज्यामिति होती है। इस प्रकार के संकरण को ‘विकर्ण संकरण’ भी कहते हैं।
$s p$ संकर कक्षकों के दो उभरे हुए धन लोब (पालि) तथा अत्यंत छोटे ऋण लोब विपरीत दिशाओं में $z$-अक्ष की ओर दृष्ट होते हैं। इसके कारण प्रभावी अतिव्यापन होता है, जिसके फलस्वरूप प्रबलतर आबंध निर्मित होते हैं।
sp संकरण वाले अणुओं के उदाहरण
$\mathbf{B e C l} _{2}$ - तलस्थ अवस्था में $\mathrm{Be}$ का इलेक्ट्रॉनी विन्यास $1 s^{2}$ $2 s^{2}$ होता है। उत्तेजित अवस्था में एक $2 s$ इलेक्ट्रॉन रिक्त $2 p$ कक्षक में $\mathrm{Be}$ की द्वि-संयोजकता के कारण प्रोन्नत (Promote) हो जाता है। एक $2 s$ कक्षक तथा एक $2 p$ कक्षक संकरित होकर दो $s p$ संकर कक्षक बनाते हैं। ये $180^{\circ}$ का कोण बनाते हैं। प्रत्येक $s p$ संकर कक्षक क्लोरीन के $2 p$ कक्षक से अक्षीय अतिव्यापन द्वारा दो $\mathrm{Be}-\mathrm{Cl}$ सिग्मा आबंध बनाते हैं। इसे चित्र 4.10 में दर्शाया गया है।
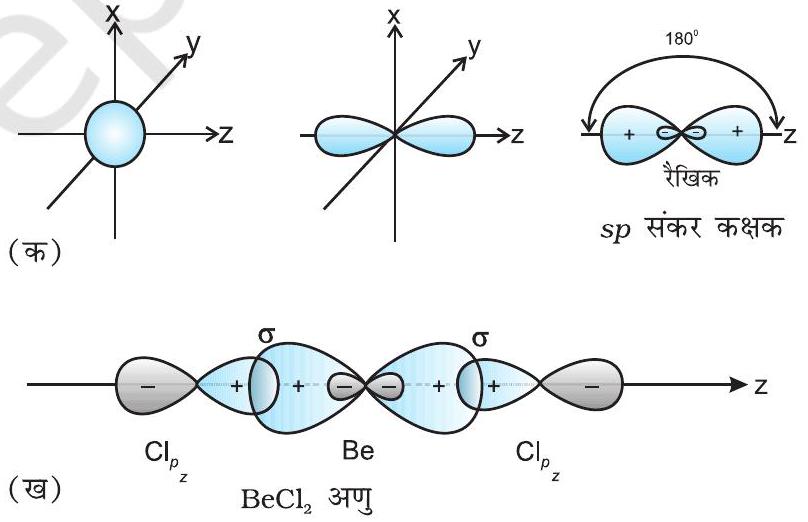
चित्र 4.10 (क) $s$ तथा $p$ कक्षकों द्वारा $s p$ संकर कक्षकों का निर्माण (ख) $\mathrm{BeCl} _{2}$ रैखिक अणु का विरचन
(II) $s^{2}$ संकरण- संकरण के इस प्रकार में एक $s$ कक्षक तथा दो $p$ कक्षक संकरित होकर तीन समान $s p^{2}$ संकर कक्षकों का निर्माण करते हैं। उदाहरण के लिए- $\mathrm{BCl} _{3}$ के अणु में केंद्रीय बोरॉन परमाणु की तलस्थ अवस्था विन्यास $1 \mathrm{~s}^{2}$ $2 s^{2} 2 p^{1}$ होता है। उत्तेजित अवस्था में एक $2 s$ इलेक्ट्रॉन रिक्त $2 p$ कक्षक में प्रोन्नत हो जाता है, जिसके परिणामस्वरूप बोरॉन में तीन अयुग्मित इलेक्ट्रॉन उपस्थित होते हैं। तीन (एक $2 s$ तथा दो $2 p$ ) कक्षक संकरित होकर तीन $s p^{2}$ संकर कक्षक बनाते हैं। तीन संकर कक्षक त्रिकोणीय समतली व्यवस्था में होते हैं तथा क्लोरीन परमाणुओं के $2 p$ कक्षकों से अतिव्यापन द्वारा तीन $\mathrm{B}-\mathrm{Cl}$ आबंध बनाते हैं। इसलिए $\mathrm{BCl} _{3}$ (चित्र 4.11) अणु की त्रिकोणीय समतली ज्यामिति होती है, जिसमें $\mathrm{Cl}-\mathrm{B}-\mathrm{Cl}$ आबंध कोण $120^{\circ}$ का होता है।
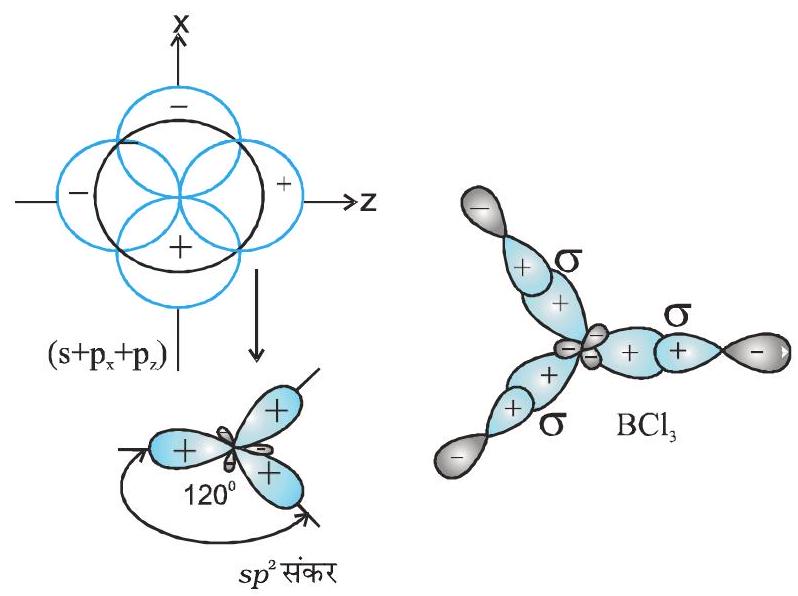
चित्र 4.11 $\mathrm{sp}^{2}$ संकर कक्षकों तथा $\mathrm{BCl} _{3}$ अणु का निर्माण
(III) $s p^{3}$ संकरण- इस प्रकार के संकरण की व्याख्या $\mathrm{CH} _{4}$ अणु के उदाहरण द्वारा की जा सकती है। इसमें सहसंयोजी कक्ष के एक $s$ कक्षक तथा $p$ कक्षकों के संकरण से चार $s p^{3}$ संकर कक्षक बनते हैं। ये कक्षक समान ऊर्जा तथा आकार के होते हैं। प्रत्येक $s p^{3}$ कक्षक में $25 % s$-लक्षण तथा $75 %$ $p$-लक्षण होता है। $s p^{3}$ संकरण द्वारा प्राप्त चार $s p^{3}$ संकर कक्षक चतुषफलक के चार कोनों की ओर होते हैं। जैसा चित्र 4.12 में दर्शाया गया है, $s p^{3}$ संकर कक्षकों के बीच कोण का मान $109.5^{\circ}$ होता है।
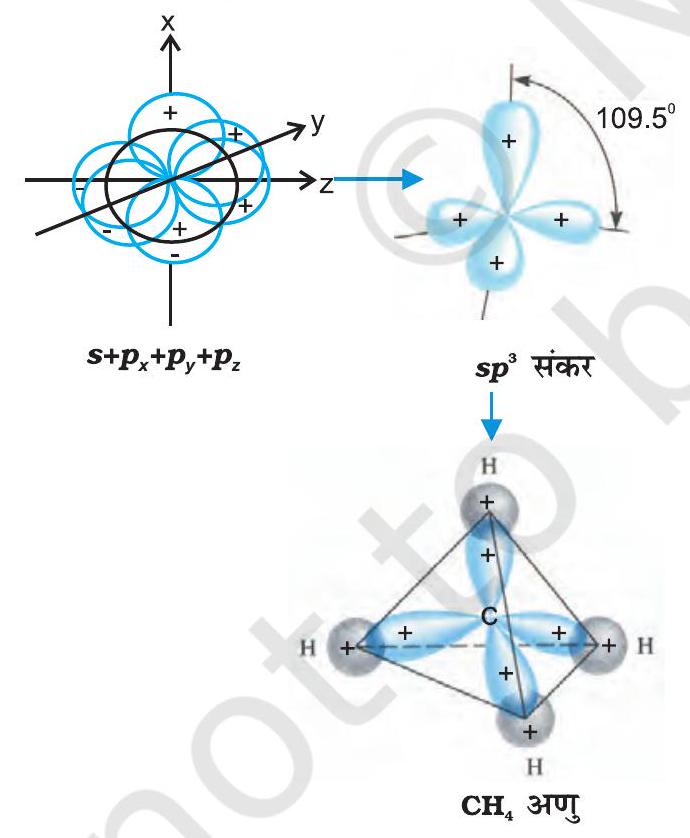
चित्र 4.12 कार्बन के $s, p_{x}, p_{y}$ और $p _{z}$ परमाणु कक्षकों के सम्मिश्रण से $s p^{3}$ संकर कक्षकों का निर्माण तथा $\mathrm{CH} _{4}$ का विरचन।
$\mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ की संरचनाओं की व्याख्या भी $s p^{3}$ संकरण द्वारा की जा सकती है। $\mathrm{NH} _{3}$ में नाइट्रोजन परमाणु का तलरूप अवस्था इलेक्ट्रॉनी विन्यास $2 \mathrm{~s}^{2} 2 p _{x}^{1} 2 p _{y}^{1} 2 p _{z}^{1}$ होता है। $s p^{3}$ संकर कक्षकों में तीन $s p^{3}$ संकर कक्षकों में अयुग्मित इलेक्ट्रॉन होता है, जबकि चौथे $s p^{3}$ संकर में एक एकांकी इलेक्ट्रॉन युग्म होता है। नाइट्रोजन के तीन $s p^{3}$ संकर कक्षक तीन हाइड्रोजन परमाणुओं के $1 s$ कक्षकों के साथ अतिव्यापन द्वारा तीन $\mathrm{N}-\mathrm{H}$ आबंध निर्मित करते हैं। हम जानते हैं कि एकांकी युग्म तथा आबंधी युग्म के बीच आबंधी युग्म की अपेक्षा प्रतिकर्षण आबंधी युग्म अधिक होता है। इसके परिणाम स्वरूप $\mathrm{NH} _{3}$ के अणु में आबंध कोण $109.5^{\circ}$ से घटकर $107^{\circ}$ हो जाता है। ऐसे अणु की ज्यामिति विकृत होकर पिरामिडी हो जाती है, जैसा चित्र 4.13 में दर्शाया गया है।
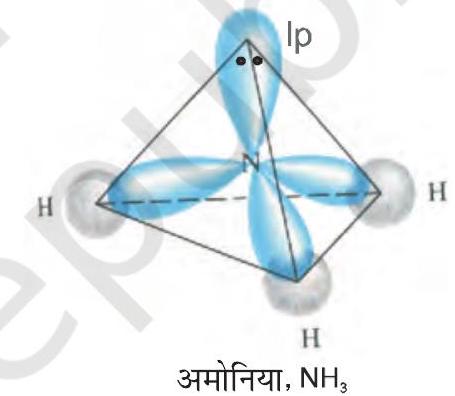
चित्र 4.13 $\mathrm{NH} _{3}$ अणु का बनना
जल के अणु में ऑक्सीजन परमाणु के चार संयोजकता कक्ष, कक्षक (एक $2 s$ तथा तीन $2 p) s p^{3}$ संकरण द्वारा चार $s p^{3}$ संकर कक्षक बनाते हैं। इनमें से दो संकर कक्षकों में एक-एक युग्म होता है। ये चार $s p^{3}$ संकर कक्षक चतुष्टफलकीय ज्यामिति प्राप्त करते हैं, जिसमें दो कोनों पर हाइड्रोजन परमाणु आबंधित होते हैं तथा अन्य दो कोनों पर एकांकी इलेक्ट्रॉन युग्म उपस्थित होते हैं। इस अणु में आबंध कोण $109.5^{\circ}$ से घटकर $104.5^{\circ}$ हो जाता है (चित्र 4.14) तथा अणु $V$-आकृति अथवा कोणीय ज्यामिति ग्रहण करता है।

चित्र 4.14 $\mathrm{H} _{2} \mathrm{O}$ अणु का बनना
4.6.2 $s p^{3}, s p^{2}$ तथा $s p$ संकरण के अन्य उदाहरण
$\mathrm{C} _{2} \mathrm{H} _{6}$ अणु में $\mathrm{sp}^{3}$ संकरण- इथेन के अणु में कार्बन के दोनों कार्बन $s p^{3}$ संकरित होते हैं। कार्बन परमाणु के चार $s p^{3}$ संकर कक्षकों में परमाणु से एक, अन्य कार्बन परमाणु के एक $s p^{3}$ संकर कक्षक से अक्षीय अतिव्यापन द्वारा $s p^{3}-s p^{3}$ सिग्मा आबंध बनाते हैं, जबकि प्रत्येक कार्बन परमाणु के अन्य तीन $s p^{3}$ संकर कक्षक हाइड्रोजन परमाणुओं के $1 s$ कक्षकों के साथ $s p^{3}-s$ सिग्मा आबंध बनाते हैं। इसके परिणामस्वरूप इथेन में $\mathrm{C}-\mathrm{C}$ आबंध लंबाई $154 \mathrm{pm}$ और $\mathrm{C}-\mathrm{H}$ आबंध लंबाई $109 \mathrm{pm}$ होती है।
$\mathrm{C} _{2} \mathrm{H} _{4}$ में $\boldsymbol{s p}^{2}$ संकरण- एथीन अणु के बनने में कार्बन परमाणु का एक $s p^{2}$ संकर कक्षक से अक्षीय अतिव्यापन द्वारा $\mathrm{C}-\mathrm{C}$ सिग्मा आबंध बनाता है, जबकि प्रत्येक कार्बन परमाणु के अन्य दो $s p^{2}$ संकर कक्षक हाइड्रोजन परमाणुओं के साथ $s p^{2}-s$ सिग्मा आबंध बनाते हैं। एक कार्बन परमाणु का असंकरित कक्षक $2 p _{x}$ अथवा $2 p _{y}$ दूसरे कार्बन परमाणु के समान कक्षक के साथ पार्श्व (Sidewise) अतिव्यापन द्वारा दुर्बल $\pi$ आबंध बनाता है जिसमें कार्बन तथा हाइड्रोजन परमाणुओं के तल के ऊपर तथा नीचे समान इलेक्ट्रॉन अभ्र होता है।
इस प्रकार एथीन अणु में $\mathrm{C}-\mathrm{C}$ के मध्य एक $s p^{2}-s p^{2}$ संकरित कक्षकों में सिग्मा $(\sigma)$ आबंध तथा एक पाई $(\pi)$ आबंध (जिसकी लंबाई $134 \mathrm{pm}$ होती है, जो $p$-कक्षकों के मध्य होता है) संकरण में प्रयोग नही होते एवं अणु के तल के लंबवत होते हैं। $\mathrm{C}-\mathrm{H}$ आबंध में $\left(\mathrm{sp}^{2}-\mathrm{s}\right)$ सिग्मा $(\sigma)$ आबंध की लंबाई $108 \mathrm{pm}$ होती है एवं $\mathrm{H}-\mathrm{C}-\mathrm{H}$ एवं $\mathrm{H}-\mathrm{C}-\mathrm{C}$ आबंध कोण क्रमशः $117.6^{\circ} 121^{\circ}$ होता है। एथीन अणु में सिग्मा $(\sigma)$ एवं पाई $(\pi)$ आबंधों का बनना चित्र 4.15 में दर्शाया गया है।

चित्र 4.15 एथीन में सिग्मा तथा $\pi$-आबंधों का बनना
$\mathrm{C} _{2} \mathrm{H} _{2}$ में $s p$ संकरण- इथाइन अणु के बनने में दोनों कार्बन परमाणु $s p$ संकरण दर्शाते हैं। उनपर दो-दो असंकरित $\left(2 p _{y}\right.$ तथा $2 p _{x}$ ) कक्षक होते हैं।
एक कार्बन परमाणु का $s p$ संकर कक्षक दूसरे कार्बन परमाणु के $s p$ संकर कक्षक से अक्षीय अतिव्यापन द्वारा $\mathrm{C}-\mathrm{C}$ सिग्मा आबंध बनाता है। बचे हुए संकर कक्षक हाइड्रोजन के अर्ध-भृत $1 \mathrm{~s}$ कक्षकों से अक्षीय अतिव्यापन द्वारा सिग्मा आबंध बनाते हैं। दोनों कार्बन परमाणुओं पर उपस्थित दो-दो असंकरित कक्षक पार्श्व अतिव्यापन द्वारा दो पाई-आबंध बनाते हैं। इस प्रकार इथाइन में दो कार्बन परमाणुओं के बीच उपस्थित त्रि-आबंध, एक सिग्मा तथा दो पाई आबंधों से बना होता है, जैसा चित्र 4.16 में दर्शाया गया है।

चित्र 4.16 एथाइन में सिग्मा तथा पाई-आबंधों का बनना
4.6.3 $d$-कक्षकों वाले तत्त्वों में संकरण
तृतीय आवर्त तत्त्वों में $s$ तथा $p$ कक्षकों के साथ-साथ $d$ कक्षक भी उपस्थित होते हैं। इन $d$ कक्षकों की ऊर्जा $3 s 3 p$ एवं $4 s, 4 p$ कक्षकों की ऊर्जा के समतुल्य होती है। $3 p$ ओर $4 s$ कक्षकों की ऊर्जा में अधिक अंतर होने के कारण $3 p, 3 d$ एवं $4 s$ कक्षकों का संकरण संभव नहीं है।
$s, p$ तथा $d$ कक्षकों के संकरण के मुख्य प्रकारों को यहाँ नीचे सारांश में दिया गया है-

(i) $\mathrm{PCl} _{5}$ का बनना ( $s p^{3} d$ संकरण )- फॉस्फोरस परमाणु $(Z=15)$ की तलस्थ अवस्था इलेक्ट्रॉनी विन्यास को नीचे दर्शाया गया है। फॉस्फोरस की आबंध निर्माण परिस्थितियों में $3 s$ कक्षक से एक इलेक्ट्रॉन अयुग्मित होकर रिक्त $3 d _{z}^{2}$ कक्षक में प्रोन्नत हो जाता है। इस प्रकार फॉस्फोरस की उत्तेजित अवस्था के विन्यास को इस प्रकार दर्शाया जा सकता है-

इस प्रकार पाँच कक्षक (एक $s$, तीन $p$ तथा एक $d$ कक्षक) संकरण के लिए उपलब्ध होते हैं। इनके संकरण द्वारा पाँच $s p^{3} d$ संकर कक्षक प्राप्त होते हैं, जो त्रिकोणीय द्वि-पिरामिड के पाँच कोनों की ओर उन्मुख होते हैं, जैसा चित्र 4.17 में दर्शाया गया है।

चित्र 4.17 $\mathrm{PCl} _{5}$ अणु की त्रिकोणीय द्वि-पिरामिडी ज्यामिति
यहाँ यह ध्यान देने योग्य बात है कि त्रिकोणीय द्विपिरामिडी ज्यामिति में सभी आबंध कोण बराबर नहीं होते हैं। $\mathrm{PCl} _{5}$ में फॉस्फोरस के पाँच $s p^{3} d$ संकर कक्षक क्लोरीन परमाणुओं के अर्ध-भृत कक्षकों से अतिव्यापन द्वारा पाँच $\mathrm{P}-\mathrm{Cl}$ सिग्माआबंध बनाते हैं। इनमें से तीन $\mathrm{P}-\mathrm{Cl}$ आबंध एक तल में होते हैं तथा परस्पर $120^{\circ}$ का कोण बनाते हैं। इन्हें ‘विषुवतीय आबंध, (Equatorial) कहते हैं। अन्य दो $\mathrm{P}-\mathrm{Cl}$ आबंध क्रमशः विषुवतीय तल के ऊपर और नीचे होते हैं तथा तल से $90^{\circ}$ का कोण बनाते हैं। इन्हें अक्षीय आबंध (Axial) कहते हैं। चूँकि अक्षीय आबंध इलेक्ट्रॉन युग्मों में विषुवतीय आबधी-युग्मों से अधिक प्रतिकर्षण अन्योन्यक्रियाएँ होती हैं, अतः ये आबंध विषुवतीय आबंधों से लंबाई में कुछ अधिक तथा प्रबलता में कुछ कम होते हैं। इसके परिणामस्वरूप $\mathrm{PCl} _{5}$ अत्यधिक क्रियाशील होता है।
(ii) $\mathrm{SF} _{6}$ का बनना ( $s p^{3} d^{2}$ संकरण )- $\mathrm{SF} _{6}$ में केंद्रीय सल्फर परमाणु की तलस्थ अवस्था इलेक्ट्रॉन विन्यास $3 s^{2} 3 p^{4}$ है। उत्तेजित अवस्था में उपलब्ध छः कक्षक, अर्थात् एक $s$, तीन $p$ तथा $d$ कक्षक अर्ध-भृत होते हैं। ये संकरण द्वारा छः $s p^{3} d^{2}$ संकर बनाते हैं, जो एक समअष्टफलक के छः कोणों की ओर प्रक्षिप्त होते हैं। ये संकर कक्षक फ्लुओरीन परमाणुओं के अर्ध-भृत कक्षकों से अतिव्यापन द्वारा छ: $\mathrm{S}-\mathrm{F}$ सिग्मा आबंध बनाते हैं। इस प्रकार $\mathrm{SF} _{6}$ अणु की एक समअष्टफलकीय ज्यामिति होती है, जैसा चित्र 4.18 में दर्शाया गया है।

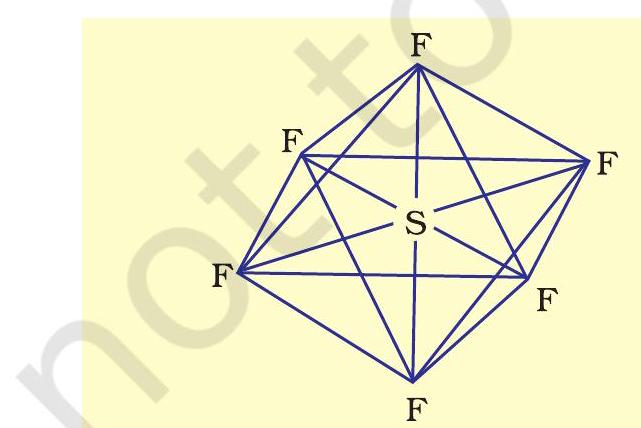
चित्र 4.18 $\mathrm{SF} _{6}$ अणु की अष्टफलकीय ज्यामिति
4.7 आण्विक कक्षक सिद्धांत
आण्विक कक्षक सिद्धांत एफ. हुंड तथा आर. एस. मुलिकन द्वारा सन् 1932 में विकसित किया गया। इस सिद्धांत के मुख्य लक्षण निम्नलिखित हैं-
(i) जिस प्रकार परमाणु में इलेक्ट्रॉन विभिन्न परमाणु कक्षकों में उपस्थित रहते हैं, उसी प्रकार अणु में इलेक्ट्रॉन विभिन्न आण्विक कक्षकों में उपस्थित रहते हैं।
(ii) आण्विक कक्षक तुल्य ऊर्जाओं एवं उपयुक्त सममिति परमाणु कक्षकों के संयोग से बनते हैं।
(iii) परमाणु कक्षक में कोई इलेक्ट्रॉन केवल एक ही नाभिक के प्रभाव में रहता है, जबकि आण्विक कक्षक में उपस्थित इलेक्ट्रॉन दो या दो से अधिक नाभिकों द्वारा प्रभावित होता है। यह संख्या अणु में परमाणुओं की संख्या पर निर्भर करती है। इस प्रकार परमाणु कक्षक एकलकेंद्रीय होता है, जबकि आण्विक कक्षक बहुकेंद्रीय होता है।
(iv) बने हुए आण्विक कक्षकों की संख्या संयोग करने वाले परमाणु कक्षकों की संख्या के बराबर होती है। जब दो परमाणु कक्षकों को मिलाया जाता है, तो दो आण्विक कक्षक प्राप्त होते हैं। इनमें से एक ‘आबंधन आण्विक कक्षक’ और दूसरा प्रतिआबंधन आण्विक कक्षक कहाजाता है।
(v) आबंधन आण्विक कक्षक की ऊर्जा कम होती है। अत: उसका स्थायित्व संगत प्रतिआबंधन आण्विक कक्षक से अधिक होता है।
(vi) जिस प्रकार किसी परमाणु के नाभिक के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण परमाणु कक्षक द्वारा दिया जाता है, उसी प्रकार किसी अणु में नाभिकों के समूह के चारों ओर इलेक्ट्रॉन प्रायिकता वितरण आण्विक कक्षक द्वारा दिया जाता है।
(vii) परमाणु कक्षकों की भाँति आण्विक कक्षकों को भी पाउली सिद्धांत तथा हुंड के नियम का पालन करते हुए ऑफबाऊ नियम के अनुसार भरा जाता है।
4.7.1 आण्विक कक्षकों का निर्माण : परमाणु-कक्षकों का रैखिक संयोग
जैसा आप जानते हैं, तरंग यांत्रिकी के अनुसार परमाणु कक्षक को एक तरंग फलन $(\psi)$ के रूप में दर्शाया जा सकता है। यह फलन इलेक्ट्रॉन तरंग के आयाम (Amplitude) को दर्शाता है तथा इसे श्रोडिंगर समीकरण के हल द्वारा प्राप्त किया जाता है, परंतु एक से अधिक इलेक्ट्रॉन वाले निकाय के लिए श्रोडिंगर समीकरण का हल नहीं किया जा सकता। इसलिए आण्विक कक्षक, जो अणुओं के लिए एक इलेक्ट्रॉन तरंग फलन है, को श्रोडिंगर समीकरण के हल से सीधे प्राप्त करना कठिन है। इस कठिनाई का निराकरण एक सन्निकट (Approximation) विधि के सहारे किया जाता है। इस विधि को ‘परमाणु कक्षकों का रैखिक संयोग’ (Linear Combination of Atomic Orbitals, LCAO) कहते हैं।
आइए, हम एक समनाभिकीय द्वि-परमाणुक अणु, $\mathrm{H} _{2}$ पर इस विधि का अनुप्रयोग करें। मान लें कि हाइड्रोजन अणु दो हाइड्रोजन परमाणुओं $\mathrm{A}$ तथा $\mathrm{B}$ से बना है। दोनों परमाणु एक समान ही हैं, केवल सुविधा के लिए उन्हें $\mathrm{A}$ तथा $\mathrm{B}$ से चिह्नित किया गया है। प्रत्येक हाइड्रोजन परमाणु की मूल अवस्था में उसके $1 s$ कक्षक में एक इलेक्ट्रॉन होता है। इन परमाणु कक्षकों को हम तरंग फलनों $\psi _{\mathrm{A}}$ तथा $\psi _{\mathrm{B}}$ द्वारा प्रदर्शित कर सकते हैं। गणितीय रूप से आण्विक कक्षकों को परमाणु कक्षकों के रैखिक संयोग व्यक्तिगत परमाणु कक्षकों के तरंग फलनों $\psi _{\mathrm{A}}$ तथा $\psi _{\mathrm{B}}$ के योग या अंतर द्वारा किया जाता है, जैसा नीचे दर्शाया गया है।
$$ \psi_{\mathrm{MO}}=\psi_{\mathrm{A}} \pm \psi_{\mathrm{B}} $$
इस प्रकार दो आण्विक कक्षक $\sigma$ तथा $\sigma^{*}$ प्राप्त होते हैं।
$$ \begin{aligned} & \sigma=\psi_{\mathrm{A}}+\psi_{\mathrm{B}} \\ & \sigma^{*}=\psi_{\mathrm{A}}-\psi_{\mathrm{B}} \end{aligned} $$
परमाणु कक्षकों के योग से बनने वाले आण्विक कक्षक $\sigma$ को आबंधन आण्विक कक्षक तथा परमाणु कक्षकों के अंतर से बनने वाले आण्विक कक्षक, $\sigma^{*}$, को ‘प्रतिआबंधन आण्विक कक्षक’ कहते हैं (चित्र 4.19)।
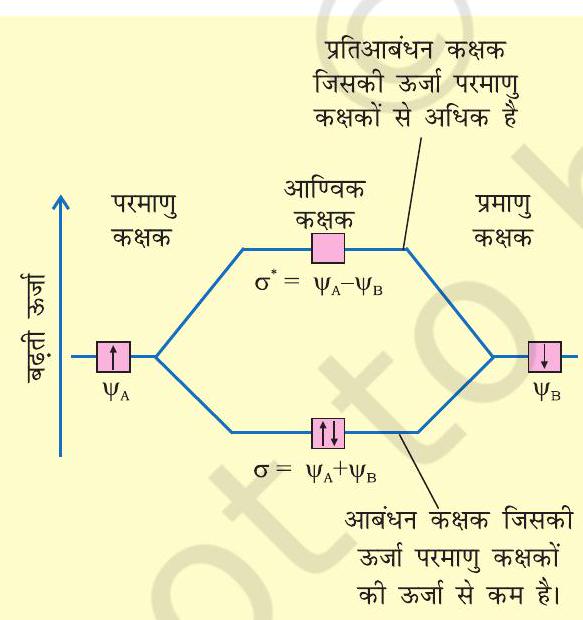
चित्र 4.19 दो परमाणु क्रमशः $A$ तथा $B$ पर केंद्रित परमाणु कक्षकों $\psi_{A}$ तथा $\psi_{B}$ के रैखिक संयोग से आबंधन $(\sigma)$ तथा प्रतिआबंधन $\left(\sigma^{*}\right)$ आण्विक कक्षकों का निर्माण।
गुणात्मक तौर पर आण्विक कक्षकों का बनना संयोग करने वाले परमाणुओं के इलेक्ट्रॉन तरंगों के रचनात्मक (Constructive) तथा विनाशी (Destructive) व्यतिकरण (Interference) के रूप में समझा जा सकता है। आबंधन आण्विक कक्षक के निर्माण में आबंधी परमाणुओं की दो इलेक्ट्रॉन तरंगें एक दूसरे को प्रबलित करती हैं, अर्थात् इनमें रचनात्मक व्यतिकरण होता है। दूसरी ओर प्रतिआबंधन आण्विक कक्षक के निर्माण में ये इलेक्ट्रॉन तरंगें एक-दूसरे को निरस्त करती हैं, अर्थात् इनमें विनाशी व्यतिकरण होता है। इनके परिणामस्वरूप आबंधन आण्विक कक्षक में अधिकांश इलेक्ट्रॉन घनत्व आबंधित परमाणुओं के बीच अवस्थित होता है। नाभिकों के बीच प्रतिकर्षण बहुत कम होता है, जबकि प्रतिआबंधी आण्विक कक्षक में अधिकांश इलेक्ट्रॉन घनत्व दोनों नाभिकों के बीच के क्षेत्र से दूर अवस्थित होता है। वास्तव में दोनों नाभिकों के मध्य एक निस्पंद तल (Nodal Plane) होता हैं, जहाँ पर इलेक्ट्रॉन घनत्व शून्य होता है। अत: नाभिकों के बीच उच्च प्रतिकर्षण होता है। आबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉन नाभिकों को परस्पर बांधे रखने की प्रवृत्ति रखते हैं। अतः ये अणु को स्थायित्व प्रदान करते हैं। इस प्रकार एक आबंधन आण्विक कक्षक उन परमाणु कक्षकों से सदैव कम ऊर्जा रखता है, जिनके संयोग से वह बनता है। इसके विपरीत प्रतिआबंधन आण्विक कक्षक में इलेक्ट्रॉन अणु को अस्थायी कर देते हैं। इलेक्ट्रॉनों एवं नाभिकों के बीच आकर्षण इस कक्षक में इलेक्ट्रॉनों के बीच परस्पर प्रतिकर्षण से कम होता है और इससे ऊर्जा में सकल वृद्धि होती है।
यहाँ ध्यान देने योग्य बात यह है कि प्रतिआबंधन कक्षक की ऊर्जा संयोग करने वाले परमाणु कक्षकों की ऊर्जा से उतनी मात्रा में अधिक हो जाती है, जितनी मात्रा में आबंधन आण्विक कक्षक की ऊर्जा कम होती है। इस प्रकार दोनों आण्विक कक्षकों की कुल ऊर्जा वही रहती है, जो दो मूल परमाणु-कक्षकों की होती है।
4.7.2 परमाणु कक्षकों के संयोग की शर्तें
परमाणु कक्षकों के रैखिक संयोग से आण्विक कक्षकों के निर्माण के लिए निम्नलिखित शर्तें अनिवार्य हैं-
1. संयोग करने वाले परमाणु कक्षकों की ऊर्जा समान या लगभग समान होनी चाहिए। इसका तात्पर्य यह है कि एक $1 s$ कक्षक दूसरे $1 \mathrm{~s}$ कक्षक से संयोग कर सकता है परंतु $2 \mathrm{~s}$ कक्षक से नहीं, क्योंकि $2 \mathrm{~s}$ कक्षक की ऊर्जा $1 \mathrm{~s}$ कक्षक की(क) ऊर्जा से कहीं अधिक होती है। यह सत्य नहीं है यदि परमाणु $\mathrm{Z}$-अक्ष को आण्विक अक्ष मानते हैं। यहाँ यह तथ्य महत्त्वपूर्ण है भिन्न प्रकार के हैं। कि समान या लगभग समान ऊर्जा वाले परमाणु कक्षक केवल
2. संयोग करने वाले परमाणु कक्षकों की आण्विक अक्ष तभी संयोग करेंगे, जब उनकी सममिति समान है, अन्यथा: के परितः समान सममिति होनी चाहिए। परिपाटी के अनुसार नहीं। उदाहरणार्थ- $2 p_{z}$ परमाणु-कक्षक दूसरे परमाणु के $2 p_{z}$ कक्षक से संयोग करेगा, परंतु $2 p_{x}$ या $2 p_{y}$ कक्षकों से नहीं, क्योंकि उनकी सममितियाँ समान नहीं हैं।
3. संयोग करने वाले परमाणु कक्षकों को अधिकतम अतिव्यापन करना चाहिए। जितना अधिक अतिव्यापन होगा, आण्विक कक्षकों के नाभिकों के बीच इलेक्ट्रॉन घनत्व उतना ही अधिक होगा।
4.7.3 आण्विक कक्षकों के प्रकार
द्वि-परमाणुक अणुओं के आण्विक कक्षकों को $\sigma$ (सिग्मा), $\pi$ (पाई), $\delta$ (डेल्टा) आदि द्वारा नामित किया जाता है। इस नामकरण में सिग्मा आण्विक कक्षक आबंध अक्ष के परितः सममित होते हैं, जबकि $\pi$ आण्विक कक्षक सममित नहीं होते। उदाहरण के लिए- दो नाभिकों पर केंद्रित $1 \mathrm{~s}$ कक्षकों का रैखिक संयोग दो आण्विक कक्षकों को उत्पन्न करता है। जो आबंध अक्ष के परितः सममित होते हैं। इन्हें $\sigma _{1 s}$ तथा $\sigma _{1 s^{\ast}}$ आण्विक कक्षक कहते है [(चित्र 4.20(अ))]। यदि अंतरनाभिकीय अक्ष को $z$-दिशा में लिया जाए, तो यह देखा जा सकता है कि दो परमाणुओं के $2 p _{z}$ कक्षकों के रैखिक संयोग से भी दो सिग्मा आण्विक कक्षक उत्पन्न होंगे। इन्हें $\sigma 2 p _{z}$ तथा $\sigma^{\ast} 2 p _{z}$ से निरूपित करते हैं [चित्र 4.20 ख]।
$2 p _{x}$ तथा $2 p _{y}$ कक्षकों के अतिव्यापन से मिलने वाले आण्विक कक्षक आबंध कक्ष के परितः सममित नहीं होते। ऐसा आण्विक तल के ऊपर धनात्मक लोब तथा आण्विक तल के नीचे ऋणात्मक लोब होने के कारण होता है। ऐसे आण्विक कक्षकों को $\pi$ और $\pi \ast$ द्वारा चिह्नित करते हैं [चित्र 4.20 ग]। आबंधन आण्विक कक्षक में अंतरानाभिक अक्ष के ऊपर एवं नीचे अधिकतम इलेक्ट्रॉन घनत्व रहता है, परंतु प्रतिबंधन आण्विक कक्षक $\pi \ast$ में नाभिकों के मध्य एक नोड़ होता है।
4.7.4 आण्विक कक्षकों का ऊर्जा-स्तर आरेख
हमने देखा कि दो परमाणुओं पर उपस्थित $1 \mathrm{~s}$ परमाणु कक्षक संयोग द्वारा दो आण्विक कक्षकों का निर्माण करते हैं, जिन्हें $\sigma 1 s$ तथा $\sigma^{\ast} 1 s$ नामित किया जाता है। इसी प्रकार दो परमाणुओं के आठ परमाणु कक्षक $(2 s$ तथा $2 p$ ) रैखिक संयोग द्वारा निम्नलिखित आठ आण्विक कक्षकों का निर्माण करते हैं-

चित्र 4.20 (क) $1 s$ परमाणु कक्षकों (ख) $2 p_{z}$ परमाणु कक्षकों तथा (ग) $2 p_{x}$ परमाणु कक्षकों के संयोगों से बने आबंधन एवं प्रतिआबंधन आण्विक कक्षकों की रूपरेखा तथा उनकी ऊर्जाएँ
$\begin{array}{llllll} \text{प्रतिआबंधी आण्विक कक्षक } & \mathrm{MOs} & \sigma^* 2 s & \sigma^* 2 p_z & \pi^* 2 p_x & \pi^* 2 p_y \\ \text { आबंधी आण्विक कक्षक } & \mathrm{MOs} & \sigma 2 \mathrm{~s} & \sigma 2 p_{z} & \pi 2 p_{x} & \pi 2 p_{y}\end{array}$
इन आण्विक कक्षकों के ऊर्जा-स्तर प्रायोगिक तौर पर स्पेक्ट्रमी विधि द्वारा प्राप्त किए जाते हैं। द्वितीय आवर्त के तत्त्वों के समनाभिकीय द्विपरमाणुक अणुओं $\left(\mathrm{O} _{2}, \mathrm{~F} _{2}\right)$ के आण्विक कक्षकों की ऊर्जा का बढ़ता क्रम इस प्रकार है-
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\sigma 2 p_z < \left(\pi 2 p_x = \pi 2 p_y\right) $
$<\left(\pi^* 2 p_x=\pi^* 2 p_y\right) < \sigma^* 2 p_z$
द्वितीय आवर्त के शेष अणुओं (जैसे- $\mathrm{Li} _{2}, \mathrm{Be} _{2}, \mathrm{~B} _{2}$, $\mathrm{C} _{2}, \mathrm{~N} _{2}$ ) के द्विपरमाणुक अणुओं के लिए आण्विक कक्षकों की ऊर्जा का क्रम ऊपर दिए गए क्रम से भिन्न होता है। उदाहरण के लिए- $\mathrm{B} _{2}, \mathrm{C} _{2}, \mathrm{~N} _{2}$ आदि द्विपरमाणुक अणुओं के आण्विक कक्षकों का प्रायोगिक तौर पर निर्धारित ऊर्जा-क्रम इस प्रकार है-
$\sigma 1 s<\sigma^* 1 s<\sigma 2 s<\sigma^* 2 s<\left(\pi 2 p_x=\pi 2 p_y\right)$
$<\sigma 2 p_z<\left(\pi^* 2 p_x=\pi^* 2 p_y\right)<\sigma^* 2 p_z$
आणिवक कक्षकों की ऊर्जा के क्रमों में महत्त्वपूर्ण अंतर यह है कि $\sigma 2 p_{z}$ कक्षक की ऊर्जा $\pi 2 p_{x}$ तथा $\pi 2 p_{y}$ आण्विक कक्षकों से अधिक होती है।
4.7.5 इलेक्ट्रॉनी विन्यास तथा आणिवक व्यवहार
विभिन्न आण्विक कक्षकों में इलेक्ट्रॉनों का वितरण ‘इलेक्ट्रॉनिक विन्यास’ कहलाता है। इलेक्ट्रॉनों को कक्षकों की ऊर्जा के बढ़ते हुए क्रम में भरा जाता है।अणु के इलेक्ट्रॉनिक विन्यास से अणु के बारे में महत्त्वपूर्ण सूचना प्राप्त हो सकती है, जैसा आगे विवेचित है।
अणुओं का स्थायित्व : यदि आबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या $\mathrm{N} _{b}$ तथा प्रतिआबंधन कक्षकों में संख्या $\mathrm{N} _{a}$ हो, तो
(i) अणु स्थायी होगा, यदि $\mathrm{N} _{b}>\mathrm{N} _{a}$ हो
(ii) अणु अस्थायी होगा, यदि $\mathrm{N} _{a}>\mathrm{N} _{b}$ हो
(i) में आबंधन इलेक्ट्रॉनों की संख्या अधिक होने के कारण आबंधी प्रभाव प्रबलतम होता है, जिससे एक स्थायी अणु प्राप्त होता है। दूसरी ओर (ii) में प्रति-आबंधन प्रभाव प्रबल होता है, जिसके परिणामस्वरूप अणु अस्थायी होता है।
आबंध कोटि (Bond Order):
आबंध कोटि को आबंधी आण्विक कक्षकों एवं प्रतिआबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या के अंतर के आधे के रूप में परिभाषित किया जाता है-
$\text { आबंध कोटि }=\frac{1}{2}\left(N_{b}-N_{a}\right)$
आबंध कोटि किसी अणु में उपस्थित सहसंयोजी आबंधों की संख्या बताती है। यदि $\mathrm{N} _{\mathrm{b}}>\mathrm{N} _{\mathrm{a}}$ हो, तो आबंध कोटि धनात्मक होगी तथा अणु स्थायी होगा और यदि आबंध कोटि ॠणात्मक $\left(\mathrm{N} _{b}<\mathrm{N} _{a}\right)$ या शून्य $\left(\mathrm{N} _{b}=\mathrm{N} _{a}\right)$ हो, तो अणु अस्थायी होगा।
आबंध की प्रकृति
जैसा बताया गया है, आबंध-कोटि किसी अणु में उपस्थित सहसंयोजी आबंधों की संख्या बताती है। उदाहरणार्थ- यदि आबंध कोटि 1,2 या 3 हो, तो उसमें क्रमशः एकल, द्वि अथवा त्रि आबंध होंगे।
आबंध-लंबाई
सामान्यतः किसी अणु में दो परमाणुओं के बीच आबंध कोटि आबंध लंबाई का एक सन्निकट माप होता हैं। आबंध लंबाई आबंध-कोटि के व्युत्क्रमानुपी होती है। जैसे-जैसे आबंध कोटि बढ़ती है, वैसे-वैसे आबंध लंबाई घटती जाती है।
चुंबकीय स्वभाव
यदि किसी अणु के सभी आण्विक कक्षक द्वि-पूरित युग्मित हों, तो पदार्थ प्रतिचुंबकीय (Diamagnetic) होता है। ऐसे अणु चुंबकीय क्षेत्र में प्रतिकर्षित होते हैं, परंतु यदि किसी अणु के एक या अधिक आण्विक कक्षकों में अयुग्मित इलेक्ट्रॉन हों, तो वह अणु अनुचुंबकीय (Paramagnetic) होता है। ऐसे अणु चुंबकीय क्षेत्र में आकर्षित होते हैं।
4.8 समनाभिकीय द्विपरमाणुक अणुओं में आबंधन
इस खंड में हम कुछ समनाभिकीय अणुओं में आबंधन की चर्चा करेंगे।
$1.$ हाइड्रोजन अणु $\left(\mathrm{H} _{2}\right)$ : यह हाइड्रोजन के दो परमाणुओं के संयोजन से बनता है। प्रत्येक हाइड्रोजन के $1 \mathrm{~s}$ कक्षक में एक इलेक्ट्रॉन होता है। अतः हाइड्रोजन के अणु में कुल दो इलेक्ट्रॉन होंगे, जो $\sigma 1 \mathrm{~s}$ आण्विक कक्षक में उपस्थित होंगे। हाइड्रोजन अणु का इलेक्ट्रॉनिक विन्यास होगा।
$$ \mathrm{H} _{2}:(\sigma 1 s)^{2} $$
हाइड्रोजन अणु की आबंध कोटि को इस प्रकार परिकलित किया जा सकता है।
$$\text {आबंध कोटि} =\frac{N_{b}-N_{a}}{2}=\frac{2-0}{2}=1$$
इसका अर्थ यह है कि हाइड्रोजन अणु में हाइड्रोजन के दो परमाणु एक-दूसरे से एकल सहसंयोजी आबंध द्वारा आबंधित होते हैं। हाइड्रोजन अणु की वियोजन ऊर्जा $438 \mathrm{~kJ} \mathrm{~mol}^{-1}$ पाई गई है तथा आबंध लंबाई का प्रायोगिक मान $74 \mathrm{pm}$ है। चूँकि हाइड्रोजन अणु में कोई अयुग्मित इलेक्ट्रॉन नहीं है, इसलिए यह प्रतिचुंबकीय है।
2. हीलियम अणु $\left(\mathrm{He} _{2}\right)$ : हीलियम परमाणु का इलेक्ट्रॉनिक विन्यास $1 \mathrm{~s}^{2}$ है। प्रत्येक हीलियम परमाणु में दो इलेक्ट्रॉन होते हैं, अर्थात् $\mathrm{He} _{2}$ अणु में कुल चार इलेक्ट्रॉन होंगे। ये इलेक्ट्रॉन $\sigma 1 \mathrm{~s}$ तथा $\sigma 1 \mathrm{~s}$ आण्विक कक्षकों में भरे जाएँगे तथा $\mathrm{He} _{2}$ का इलेक्ट्रॉनिक विन्यास होगा।
$\mathrm{He} _{2}:(\sigma 1 s)^{2}(\sigma * 1 s)^{2}$ तथा
$\mathrm{He} _{2}$ की आबंध कोटि $=\frac{1}{2}(2-2)=0$
चूँकि $\mathrm{He} _{2}$ के लिए आबंध कोटि शून्य है, अतः यह अणु अस्थायी होगा तथा इसका अस्तित्व नहीं होगा!
इसी प्रकार यह दर्शाया जा सकता है कि $\mathrm{Be} _{2}$ अणु $\left[(\sigma 1 s)^{2}(\sigma * 1 s)^{2}\right.$ $\left.(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\right]$ भी नहीं बनेगा।
3. लीथियम अणु $\left(\mathrm{Li} _{2}\right)$ : लीथियम का इलेक्ट्रॉनिक विन्यास $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{1}$ है। लीथियम के प्रत्येक परमाणु में तीन इलेक्ट्रॉनिक होंगे। इसलिए $\mathrm{Li} _{2}$ अणु का इलेक्ट्रॉनिक विन्यास होगा-
$$ \mathrm{Li} _{2}:(\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}(\sigma 2 s)^{2} $$
इस विन्यास को $\mathrm{KK}(\sigma 2 s)^{2}$ द्वारा भी प्रदार्शित किया जाता है, जहाँ $\mathrm{KK}$, पूर्ण $\mathrm{K}$ कोश रचना $\left((\sigma 1 s)^{2}\left(\sigma^{*} 1 s\right)^{2}\right)$ दर्शाता है।
$\mathrm{Li} _{2}$ अणु के इलेक्ट्रॉनिक विन्यास से स्पष्ट है कि इसमें चार इलेक्ट्रॉन आबंधी आण्विक कक्षकों में तथा दो इलेक्ट्रॉन प्रतिआबंधी आण्विक कक्षक में उपस्थित हैं। अतः इसकी आबंध काटी $=\frac{1}{2}(4-2)=1$ होगी। इसका अभिप्राय यह है कि $\mathrm{Li} _{2}$ अणु स्थायी है। चूँकि इसमें कोई अयुग्मित इलेक्ट्रॉन नही है, इसलिए यह प्रतिचुंबकीय होगा। वास्तव में यह पाया गया है कि वाष्प प्रावस्था में $\mathrm{Li} _{2}$ अणुओं का अस्तित्व होता है, जो प्रतिचुंबकीय होते हैं।
4. कार्बन अणु $\left(\mathrm{C} _{2}\right)$ : कार्बन का इलेक्ट्रॉनिक विन्यास $1 s^{2} 2 s^{2} 2 p^{2}$ है। $\left(\mathrm{C} _{2}\right)$ के अणु में कुल 12 इलेक्ट्रॉन होंगे। तथा इसका इलेक्ट्रॉनिक विन्यास होगा।
$\mathrm{C}_2:(\sigma 1 \mathrm{~s})^{2}\left(\sigma^{*} 1 \mathrm{~s}\right)^{2}(\sigma * 2 \mathrm{~s})^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
अथवा $K K(\sigma 2 s)^{2}(\sigma * 2 s)^{2}\left(\pi 2 \mathrm{p}_x^{2}=\pi 2 \mathrm{p}_y^{2}\right)$
$\mathrm{C} _{2}$ की आबंध कोटि $=\frac{1}{2}(8-2)=2$ तथा $\mathrm{C} _{2}$ को प्रतिचुंबकीय होना चाहिए! वस्तुतः वाष्प अवस्था में $\mathrm{C} _{2}$ प्रतिचुंबकीय है $\mathrm{C} _{2}$ के अणुओं में दोनों आबंध पाई-आबंध होते है, क्योंकि दो $\pi$.आबंधन आण्विक कक्षकों में चार इलेक्ट्रॉन उपस्थित होते हैं। अधिकांश अन्य अणुओं में द्वि-आबंध, एक सिग्मा तथा एक पाई आबंध से बना होता है। समान रूप से $\mathrm{N} _{2}$ अणु में आबंधन को समझाया जा सकता है।
5. ऑक्सीजन अणु $\left(\mathrm{O} _{2}\right)$ : ऑक्सीजन परमाणु का इलेक्ट्रॉनिक विन्यास $1 \mathrm{~s}^{2} 2 \mathrm{~s}^{2} 2 \mathrm{p}^{4}$ है। चूँकि प्रत्येक ऑक्सीजन परमाणु में 8 इलेक्ट्रॉन होते हैं, ऑक्सीजन अणु में कुल 16 इलेक्ट्रॉन होंगे। $\mathrm{O} _{2}$ अणु का इलेक्ट्रॉनिक विन्यास होगा-
$\mathrm{O} _{2}:(\sigma 1 s)^{2}\left(\sigma^{\ast} 1 s\right)^{2}(\sigma 2 s)^{2}\left(\sigma^{\ast} 2 s\right)^{2}\left(\sigma 2 p _{z}\right)^{2}$
$\left(\pi 2 p_{x}{ }^{2} \equiv \pi 2 p_{y}{ }^{2}\right)\left(\pi * 2 p_{x}{ }^{1} \equiv \pi * 2 p_{y}{ }^{1}\right)$
अथवा $\mathrm{O}^{2}:\left[\begin{array}{c}\mathrm{KK}(\sigma 2 \mathrm{~s})^{2}\left(\sigma 2 p_S\right)^{2}\left(\sigma 2 p_z\right)^{2} \\ \left(\pi 2 p_x^{2} \equiv \pi 2 p_y^{2}\right),\left(\pi * 2 \mathrm{p}_x^{1} \equiv \pi * 2_y^{1}\right)\end{array}\right]$
$\mathrm{O} _{2}$ के इलेक्ट्रॉनिक विन्यास से यह स्पष्ट है कि इसमें 10 इलेक्ट्रॉन आबंधन आण्विक कक्षकों में तथा 6 इलेक्ट्रॉन प्रतिआबंधन आण्विक कक्षकों में उपस्थित होते हैं। अतः इसकी आबंध-कोटि होगी-
$\text { आबंध-कोटि }=\frac{1}{2}(\mathrm{Nb}-\mathrm{Na})=\frac{1}{2}[10-6]=2$
इसलिए $\mathrm{O} _{2}$ के अणु में ऑक्सीजन परमाणु एक द्वि-आबंध द्वारा जुड़े होते हैं। इसके ऑक्सीजन अणु के $\pi^{\ast} 2 p _{x}$ तथा $\pi^{\ast} 2 p _{y}$ आण्विक कक्षकों में एक-एक अयुग्मित इलेक्ट्रॉन उपस्थित होते हैं। इसके अनुसार, ऑक्सीजन अणु को अनुचुंबकीय होना चाहिए। ऐसा प्रायोगिक तौर पर पाया भी गया है। इस प्रकार आण्विक कक्षक सिद्धांत ऑक्सीजन के अनुचुंबकीय व्यवहार की व्याख्या करने में समर्थ है।
इसी प्रकार आवर्त सारणी के द्वितीय आवर्त के अन्य समनाभिकीय द्विपरमाणुक अणुओं के इलेक्ट्रॉनिक विन्यास लिखे जाकते हैं। $\mathrm{B} _{2}$ से $\mathrm{Ne} _{2}$ तक के अणुओं के लिए आण्विक कक्षक विन्यास तथा आण्विक गुण चित्र 4.21 में दिए गए हैं। आण्विक कक्षकों का क्रम तथा उनमें इलेक्ट्रॉनों की संख्या दर्शाई गई है। आबंध-ऊर्जा, आबंध-कोटि, चुंबकीय गुण तथा संयोजी इलेक्ट्रॉन विन्यास कक्षक आरेखों के नीचे प्रदार्शित हैं।
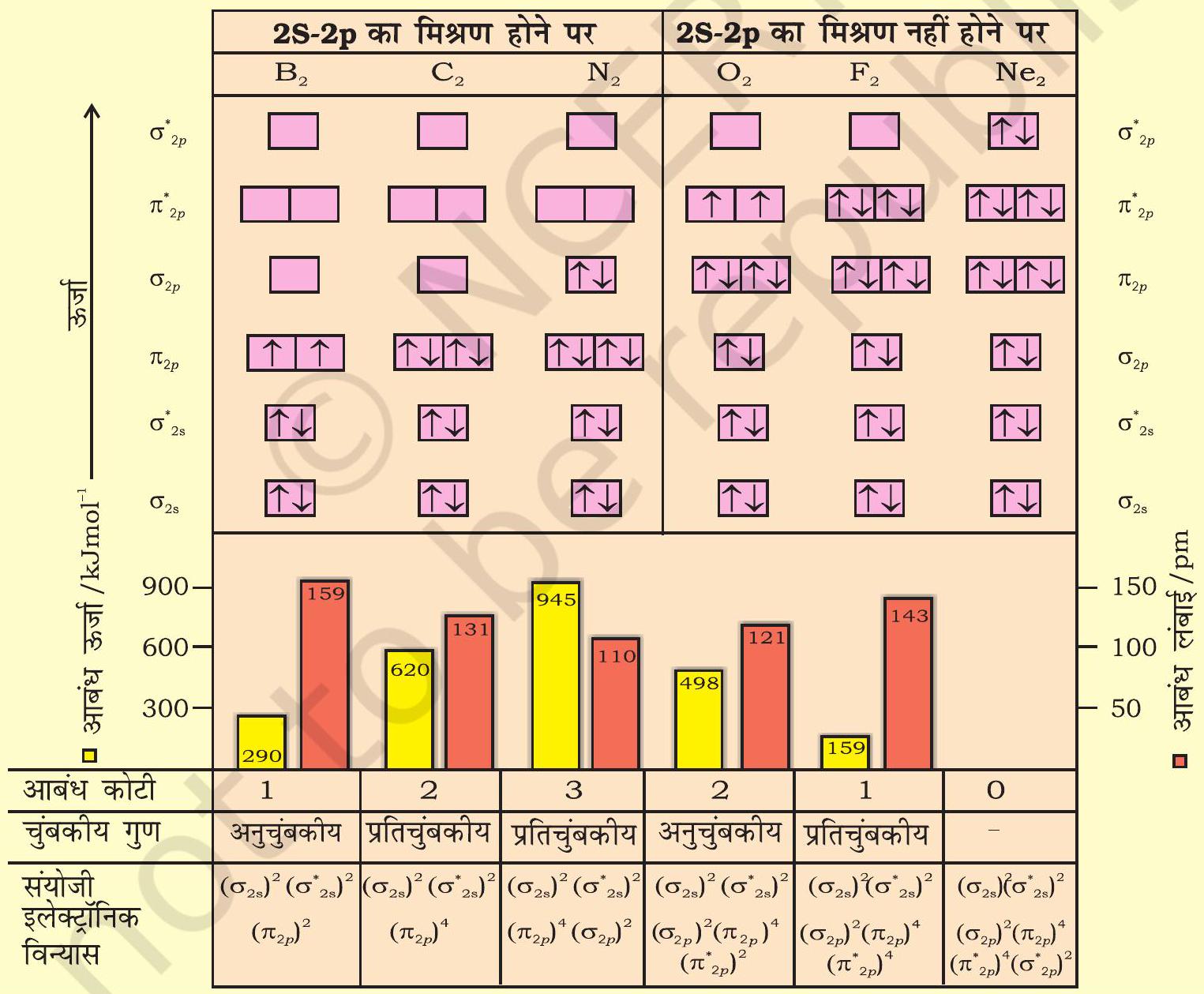
चित्र 4.21 $\mathrm{~B} _{2}$ से $\mathrm{Ne} _{2}$ तक के लिए आण्विक कक्षक तथा आण्विक गुण
4.9 हाइड्रोजन आबंधन
नाइट्रोजन, ऑक्सीजन तथा फ्लुओरीन-ये तीन अत्यधिक विद्युत् ॠणात्मक तत्त्व जब परमाणु सहसंयोजक आबंध द्वारा हाइड्रोजन परमाणु से जुड़े होते हैं, तब सहसंयोजी आबंध के इलेक्ट्रॉन अधिक विद्युत् ॠणात्मक तत्त्व की ओर स्थानांतरित हो जाते हैं। फलस्वरूप प्राप्त आंशिक धनावेशित हाइड्रोजन परमाणु किसी दूसरे विद्युत् ऋणात्मक परमाणु के साथ एक नया आबंध बनाता है। इस आबंध को ‘हाइड्रोजन आबंध’ कहते हैं। यह आबंध सहसंयोजी आबंध से दुर्वल होता है। उदाहरणार्थ- $\mathrm{HF}$ में एक अणु के हाइड्रोजन परमाणु तथा दूसरे अणु के फ्लुओरीन परमाणु के बीच हाइड्रोजन आबंध बनता है। इसे इस प्रकार दर्शाया जा सकता है-
$\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{F}^{\delta-}$
यहाँ पर हाइड्रोजन आबंध दो परमाणुओं के बीच एक सेतु का कार्य करता है, जो एक परमाणु को सहसंयोजक आबंध तथा दूसरे को हाइड्रोजन आबंध द्वारा जोड़कर रखता है। हाइड्रोजन आबंध को डॉटेड रेखा (……) द्वारा दर्शाते हैं, जबकि सहसंयोजन आबंध को ठोस रेखा (-) द्वारा दर्शाते हैं। इस प्रकार हाइड्रोजन आबंध को उस आकर्षण बल के रूप में परिभाषित किया जा सकता है, जो एक अणु के हाइड्रोजन परमाणु को दूसरे अणु के विद्युत् ॠणात्मक परमाणु $(\mathbf{F}, \mathbf{O}$ या $\mathbf{N})$ से बांधता है।
4.9.1 हाइड्रोजन आबंध बनने का कारण
जब हाइड्रोजन परमाणु किसी प्रबल विद्युत् ऋणात्मक तत्त्व ’ $\mathrm{X}$ ’ से आबंधित होता है, तो सहभाजित इलेक्ट्रॉन युग्म हाइड्रोजन परमाणु से दूर हो जाता है। परिणामस्वरूप हाइड्रोजन परमाणु दूसरे परमाणुओं ’ $\mathrm{X}$ ’ के सापेक्ष अत्यधिक विद्युत् धनात्मक हो जाता है। चूँकि इलेक्ट्रॉन ’ $\mathrm{X}$ ’ परमाणु की ओर स्थानांतरित हो जाते हैं, इसलिए हाइड्रोजन परमाणु आंशिक धनात्मक आवेश $(\delta+)$ ग्रहण करता है, जबकि $\mathrm{X}$ परमाणु पर आंशिक ऋणात्मक आवेश $(\delta-)$ आ जाता है। इससे एक द्विध्रुवी अणु प्राप्त होता है, जिसके बीच स्थिर वैद्युत बल होता है। इसे इस प्रकार दर्शाया जा सकता है-
$\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}\text{ - - - }\mathrm{H}^{\delta+}-\mathrm{X}^{\delta-}$
हाइड्रोजन आबंध का परिमाण यौगिक की भौतिक अवस्था पर निर्भर करता है। ठोस अवस्था में यह अधिकतम होता है तथा गैसीय अवस्था में न्यूनतम। इस तरह से हाइड्रोजन आबंध यौगिकों की संरचना तथा गुणधर्मों को प्रबलता से प्रभावित करते हैं।
4.9.2 हाइड्रोजन आबंधों के प्रकार
हाइड्रोजन आबंध दो प्रकार के होते हैं-
(i) अंतर-अणुक हाइड्रोजन आबंध
(ii) अंतरा-अणुक हाइड्रोजन आबंध
(1) अंतर-अणुक हाइड्रोजन आबंध- ये आबंध समान अथवा विभिन्न यौगिकों के दो अलग-अलग अणुओं के बीच बनते हैं। उदाहरणार्थ- $\mathrm{HF}$ अणु, एल्कोहॉल या जल के अणुओं के बीच हाइड्रोजन आबंध।
(2) अंतरा-अणुक हाइड्रोजन आबंध- ये आबंध एक ही अणु में उपस्थित हाइड्रोजन परमाणु तथा अधिक विद्युत् ॠणात्मक परमाणु ( $\mathrm{F}, \mathrm{O}, \mathrm{N})$ के बीच बनता है। उदाहरणार्थ- $\mathrm{O}$-नाइट्रो फिनॉल में हाइड्रोजन, जो ऑक्सीजन के मध्य रहता है।
चित्र 4.22 $o$-नाइट्रोफ़ीनॉल अणु में अंतर-अणुक हाइड्रोजन आबंध
सारांश
इलेक्ट्रो धनायनों तथा इलेक्ट्रो ऋणायनों के विरचन की क्रियाविधि को सर्वप्रथम कॉसेल ने संबंधित आयन द्वारा उत्कृष्ट गैस विन्यास की प्राप्ति के साथ संबंधित किया। आयनों के बीच वैद्युत आकर्षण के कारण स्थायित्व उत्पन्न होता है, जो वैद्युत संयोजकता का आधार है।
लूइस ने सर्वप्रथम सहसंयोजी आबंधन की व्याख्या परमाणुओं द्वारा इलेक्ट्रॉन युग्म के सहभाजन के रूप में की। इस प्रक्रिया द्वारा संबंधित परमाणु उत्कृष्ट गैस विन्यास प्राप्त करते हैं। लूइस बिंदु चिह्न किसी तत्त्व के परमाणु के संयोजकता इलेक्ट्रॉनों को दर्शाते हैं तथा लूइस बिंदु संरचनाएँ अणुओं में आबंधन का चित्रण करती हैं।
आयनिक यौगिक धनायनों तथा ऋणायनों की निश्चित क्रम में त्रिविमीय व्यवस्था होती है, जिसे ‘क्रिस्टल जालक’ कहा जाता है। क्रिस्टलीय गैसों में धनायन एवं ऋणायन के मध्य आवेश संतुलित होता है। क्रिस्टल जालक का जालक विरचन एंथैल्पी द्वारा स्थिरीकरण होता है।
दो परमाणुओं के बीच एकल सहसंयोजी आबंध का विरचन एक-एक इलेक्ट्रॉन युग्म के सहभाजन द्वारा होता है, जबकि दो या तीन इलेक्ट्रॉन युग्मों के सहभाजन के फलस्वरूप बहु आबंध निर्मित होते हैं। कुछ आबंधी परमाणुओं पर ऐसे इलेक्ट्रॉन युग्म उपस्थित होते हैं, जो आबंधन में भाग नहीं लेते। ये ‘इलेक्ट्रॉनों के एकाकी युग्म’ कहलाते हैं। लूइस बिंदु संरचना अणु में प्रत्येक परमाणु पर आबंधी युग्मों तथा एकाकी युग्मों को दर्शाती है। रासायनिक आबंधों के कुछ प्रमुख प्राचल, जैसे-आबंध एंथैल्पी, आबंध कोटि विद्युत् ऋणात्मक्ता तथा आबंध ध्रुवणता यौगिकों के गुणों को प्रभावित करते हैं।
बहुत से अणुओं तथा बहुपरमाणुक आयनों को मात्र एक लूइस संरचना द्वारा प्रदर्शित नहीं किया जा सकता है। ऐसी स्पीशीज़ के लिए अनेक संरचनाएँ लिखी जाती हैं, जिनके ढाँचे की संरचना समान होती है। ये सभी संरचनाएँ सम्मिलित रूप में अणु या आयन की वास्तविक संरचना प्रदर्शित करती हैं। यह एक महत्त्वपूर्ण तथा अति उपयोगी अवधारणा है, जिसे ‘अनुनाद’ कहा जाता है। योगदान देने वाली विहित संरचनाओं का अनुनाद संकर अणु या आयन की वास्तविक संरचना प्रदर्शित करता है।
वी. एस. ई. पी. आर. मॉडल का उपयोग अणुओं की ज्यामितीय आकृतियों के पूर्वानुमान के लिए किया जाता है। यह मॉडल इस कल्पना पर आधारित है कि अणु में इलेक्ट्रॉन युग्म एक-दूसरे को प्रतिकर्षित करते हैं। इस मॉडल के अनुसार, आण्विक ज्यामिति एकाकी युग्म-एकाकी युग्म, एकाकी युग्म-आबंधी युग्म तथा आबंधी युग्म-आबंधी युग्म प्रतिकर्षणों पर निर्भर करती हैं। इन प्रतिकर्षण बलों का क्रम इस प्रकार है- $1 \mathrm{p}-\mathrm{lp}>\mathrm{lp}-\mathrm{bp}>\mathrm{bp}-\mathrm{bp}$
सहसंयोजी आबंधन का सहसंयोजकता आबंध सिद्धांत सहसंयोजी आबंध बनने के ऊर्जा-विज्ञान पर आधारित है, जिसपर लूइस तथा वी. एस. ई. पी. आर. मॉडल प्रकाश नहीं डालते। मूलतः VB सिद्धांत कक्षकों के अतिव्यापन पर आधारित है। उदाहरणस्वरूप $-\mathrm{H} _{2}$ अणु का विरचन दो हाइड्रोजन परमाणुओं के एक इलेक्ट्रॉन वाले $1 s$ कक्षकों के अतिव्यापन के फलस्वरूप होता है। दो हाइड्रोजन परमाणु जैसे-जैसे निकट आते हैं, वैसे-वैसे निकाय की स्थितिज ऊर्जा कम होती जाती है। साम्य अंतर्नाभिकीय दूरी (आबंध लंबाई) पर निकाय की ऊर्जा न्यूनतम होती है। नाभिकों को और समीप लाने पर निकाय की ऊर्जा तेजी से बढ़ती है, अर्थात् अणु का स्थायित्व कम हो जाता है। कक्षक अतिव्यापन के कारण दोनों नाभिकों के बीच इलेक्ट्रॉन घनत्व बढ़ जाता है, जिसके कारण नाभिक आपस में पास-पास आ जाते हैं। परंतु यह पाया गया है कि केवल अतिव्यापन के आधार पर आबंध एंथैल्पी तथा आबंध लंबाइयों के वास्तविक मान प्राप्त नहीं होते हैं। इसके लिए कुछ अन्य कारकों पर भी विचार करना आवश्यक है।
बहुपरमाणुक अणुओं की विशिष्ट आकृतियों को स्पष्ट करने के लिए पॉलिंग ने परमाणु कक्षकों के संकरण की अवधारणा को प्रस्तुत किया। $\mathrm{Be}, \mathrm{B}, \mathrm{C}, \mathrm{N}$ तथा $\mathrm{O}$ के परमाणु कक्षकों के $s p, s p^{2}, s p^{3}$ संकरों के आधार पर $\mathrm{BeCl} _{2}, \mathrm{BCl} _{3}$, $\mathrm{CH} _{4}, \mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ आदि अणुओं का विरचन तथा उनकी ज्यामितीय आकृतियाँ स्पष्ट की जा सकती हैं। इसके आधार पर $\mathrm{C} _{2} \mathrm{H} _{2}$ तथा $\mathrm{C} _{2} \mathrm{H} _{4}$ आदि अणुओं में बहु-आबंधों का निर्भाण भी स्पष्ट किया जा सकता है।
आण्विक कक्षक सिद्धांत परमाणु कक्षकों के संयोग एवं व्यवस्था से संपूर्ण अणु से संबद्ध आण्विक कक्षकों के बनने के रूप में आबंधन का वर्णन करता है। आण्विक कक्षकों की संख्या संयोग करनेवाले परमाणु कक्षकों की संख्या के बराबर होती है। आबंधी आण्विक कक्षक नाभिकों के मध्य इलेक्ट्रॉन घनत्व बढ़ा देते हैं तथा इनकी ऊर्जा व्यक्तिगत परमाणु कक्षकों की ऊर्जा से कम होती है। प्रतिआबंधी आण्विक कक्षक में नाभिकों के मध्य शून्य इलेक्ट्रॉन घनत्व होता है। इन कक्षकों की ऊर्जा व्याक्तिगत परमाणु कक्षकों की अपेक्षा उच्च होती है।
अणुओं का इलेक्ट्रॉन विन्यास आण्विक कक्षकों में इलेक्ट्रॉनों को ऊर्जा के बढ़ते क्रम में भरते हुए लिखा जाता है। परमाणुओं की तरह यहाँ भी पॉउली अपवर्जन नियम तथा हुंड के नियम लागू होते हैं। यदि अणु के आबंधी आण्विक कक्षकों में इलेक्ट्रॉनों की संख्या प्रति-आबंधी आण्विक कक्षकों में उपस्थित इलेक्ट्रॉनों की संख्या से अधिक होती है, तो अणु स्थायी होता है।
जब एक हाइड्रोजन परमाणु दो अत्यंत विद्युत् ऋणात्मक परमाणुओं $(\mathrm{F}, \mathrm{N}, \mathrm{O})$ के बीच होता है, तो उसमें हाइड्रोजन आबंध बनाता है। यह अंतर-अणुक (समान या भिन्न अणुओं के अलग-अलग अणुओं के बीच) या अंतरा-अणुक (एक अणु में ही) प्रकार का हो सकता है। हाइड्रोजन आबंध कई यौगिकों की संरचनाओं तथा गुणधर्मों पर प्रबलकारी प्रभाव डालते हैं।
अभ्यास
4.1 रासायनिक आबंध के बनने की व्याख्या कीजिए।
Show Answer
Answer
/#missing
4.2 निम्नलिखित तत्त्वों के परमाणुओं के लूइस बिंदु प्रतीक लिखिए $\mathrm{Mg}, \mathrm{Na}, \mathrm{B}, \mathrm{O}, \mathrm{N}, \mathrm{Br}$.
Show Answer
Answer
/#missing
4.3 निम्नलिखित परमाणुओं तथा आयनों के लूइस बिंदु प्रतीक लिखिए। $\mathrm{S}$ और $\mathrm{S}^{2-}, \mathrm{Al}$ तथा $\mathrm{Al}^{3+}, \mathrm{H}$ और $\mathrm{H}^{-}$
Show Answer
Answer
/#missing
4.4 निम्नलिखित अणुओं तथा आयनों की लूइस संरचनाएँ लिखिए-
$\mathrm{H} _{2} \mathrm{~S}, \mathrm{SiCl} _{4}, \mathrm{BeF} _{2}, \mathrm{CO} _{3}^{2-}, \mathrm{HCOOH}$
Show Answer
Answer
/#missing
4.5 अष्टक नियम को परिभाषित कीजिए तथा इस नियम के महत्त्व और सीमाओं को लिखिए।
Show Answer
Answer
/#missing
4.6 आयनिक आबंध बनाने के लिए अनुकूल कारकों को लिखिए।
Show Answer
Answer
/#missing
4.7 निम्नलिखित अणुओं की आकृति की व्याख्या वी. एस. ई. पी. आर. सिद्धांत के अनुरूप कीजिए
$\mathrm{BeCl} _{2}, \mathrm{BCl} _{3}, \mathrm{SiCl} _{4}, \mathrm{AsF} _{5}, \mathrm{H} _{2} \mathrm{~S}, \mathrm{PH} _{3}$
Show Answer
Answer
/#missing
4.8 यद्यपि $\mathrm{NH} _{3}$ तथा $\mathrm{H} _{2} \mathrm{O}$ दोनों अणुओं की ज्यामिति विकृत चतुष्फलकीय होती है, तथापि जल में आबंध कोण अमोनिया की अपेक्षा कम होता है। विवेचना कीजिए।
Show Answer
Answer
/#missing
4.9 आबंध प्रबलता को आबंध-कोटि के रूप में आप किस प्रकार व्यक्त करेंगे?
Show Answer
Answer
/#missing
4.10 आबंध लंबाई की परिभाषा दीजिए।
Show Answer
Answer
/#missing
4.11 $\mathrm{CO} _{3}^{2-}$ आयन के संदर्भ में अनुनाद के विभिन्न पहलुओं को स्पष्ट कीजिए।
Show Answer
Answer
/#missing
4.12 नीचे दी गई संरचनाओं (1 तथा 2) द्वारा $\mathrm{H} _{3} \mathrm{PO} _{3}$ को प्रदर्शित किया जा सकता है। क्या ये दो संरचनाएँ $\mathrm{H} _{3} \mathrm{PO} _{3}$ के अनुनाद संकर के विहित (केनॉनीकल) रूप माने जा सकते है? यदि नहीं, तो उसका कारण बताइए।

Show Answer
Answer
/#missing
4.13 $\mathrm{SO} _{3}, \mathrm{NO} _{2}$ तथा $\mathrm{NO} _{3}^{-}$की अनुनाद-संरचनाएँ लिखिए।
Show Answer
Answer
/#missing
4.14 निम्नलिखित परमाणुओं से इलेक्ट्रॉन स्थानांतरण द्वारा धनायनों तथा ऋणायनों में विरचन को लूइस बिंदु-प्रतीकों की सहायता से दर्शाइए- (क) $\mathrm{K}$ तथा $\mathrm{S}$ (ख) $\mathrm{Ca}$ तथा $\mathrm{O}$ (ग) $\mathrm{Al}$ तथा $\mathrm{N}$
Show Answer
Answer
/#missing
4.15 हालाँकि $\mathrm{CO} _{2}$ तथा $\mathrm{H} _{2} \mathrm{O}$ दोनों त्रिपरमाणुक अणु हैं, परंतु $\mathrm{H} _{2} \mathrm{O}$ अणु की आकृति बंकित होती है, जबकि $\mathrm{CO} _{2}$ की रैखिक आकृति होती है। द्विध्रुव आघूर्ण के आधार पर इसकी व्याख्या कीजिए।
Show Answer
Answer
/#missing
4.16 द्विघ्रुव आधूर्ण के महत्त्वपूर्ण अनुप्रयोग बताएँ।
Show Answer
Answer
/#missing
4.17 विद्युत-ऋणात्मकता को परिभाषित कीजिए। यह इलेक्ट्रॉन बंधुता से किस प्रकार भिन्न है?
Show Answer
Answer
/#missing
4.18 ध्रूवीय सहसंयोजी आबंध से आप क्या समझते हैं? उदाहरणसहित व्याख्या कीजिए।
Show Answer
Answer
/#missing
4.19 निम्नलिखित अणुओं को आबंधों की बढ़ती आयनिक प्रकृति के क्रम में लिखिए- $\mathrm{LiF}, \mathrm{K} _{2} \mathrm{O}, \mathrm{N} _{2}, \mathrm{SO} _{2}$, तथा $\mathrm{ClF} _{3}$
Show Answer
Answer
/#missing
4.20 $\mathrm{CH} _{3} \mathrm{COOH}$ की नीचे दी गई ढाँचा-संरचना सही है, परंतु कुछ आबंध त्रुटिपूर्ण दर्शाए गए है। ऐसिटिक अम्ल की सही लूइस-संरचना लिखिए-

Show Answer
Answer
/#missing
4.21 चतुष्फलकीय ज्यामिति के अलावा $\mathrm{CH} _{4}$ अणु की एक और संभव ज्यामिति वर्ग-समतली है, जिसमें हाइड्रोजन के चार परमाणु एक वर्ग के चार कोनों पर होते है। व्याख्या कीजिए कि $\mathrm{CH} _{4}$ की अणु वर्ग-समतली नहीं होता है।
Show Answer
Answer
/#missing
4.22 यद्यपि $\mathrm{Be}-\mathrm{H}$ आबंध ध्रुवीय है, तथापि $\mathrm{BeH} _{2}$ अणु का द्विध्रुव आघूर्ण शून्य है। स्पष्ट कीजिए।
Show Answer
Answer
/#missing
4.23 $\mathrm{NH} _{3}$ तथा $\mathrm{NF} _{3}$ में किस अणु का द्विध्रुव-आघूर्ण अधिक है और क्यों?
Show Answer
Answer
/#missing
4.24 परमाणु-कक्षकों के संकरण से आप क्या समझते हैं। $s p, s p^{2}$ तथा $s p^{3}$ संकर कक्षकों की आकृति का वर्णन कीजिए।
Show Answer
Answer
/#missing
4.25 निम्नलिखित अभिक्रिया में $\mathrm{Al}$ परमाणु की संकरण अवस्था में परिवर्तन (यदि होता है, तो) को समझाइए-
$\mathrm{AlCl} _{3}+\mathrm{Cl}^{-} \rightarrow \mathrm{AlCl} _{4}^{-}$
Show Answer
Answer
/#missing
4.26 क्या निम्नलिखित अभिक्रिया के फलस्वरूप $\mathrm{B}$ तथा $\mathrm{N}$ परमाणुओं की संकरण-अवस्था में परिवर्तन होता है?
$\mathrm{BF} _{3}+\mathrm{NH} _{3} \rightarrow \mathrm{F} _{3} \mathrm{~B} . \mathrm{NH} _{3}$
Show Answer
Answer
/#missing
4.27 $\mathrm{C} _{2} \mathrm{H} _{4}$ तथा $\mathrm{C} _{2} \mathrm{H} _{2}$ अणुओं में कार्बन परमाणुओं के बीच क्रमशः द्वि-आबंध तथा त्रि-आबंध के निर्माण को चित्र द्वारा स्पष्ट कीजिए।
Show Answer
Answer
/#missing
4.28 निम्नलिखित अणुओं में सिग्मा $(\sigma)$ तथा पाई $(\pi)$ आबंधों की कुल संख्या कितनी है?
(क) $\mathrm{C} _{2} \mathrm{H} _{2}$ (ख) $\mathrm{C} _{2} \mathrm{H} _{4}$
Show Answer
Answer
/#missing
4.29 $\mathrm{x}$-अक्ष को अंतर्नाभिकीय अक्ष मानते हुए बताइए कि निम्नलिखित में कौन से कक्षक सिग्मा $(\sigma)$ आबंध नहीं बनाएँगे और क्यों? (क) $1 s$ तथा $1 s$ (ख) $1 s$ तथा $2 p_{\mathrm{x}}$ (ग) $2 p_{\mathrm{y}}$ तथा $2 p_{\mathrm{y}}$ (ल) $1 s$ तथा $2 s$
Show Answer
Answer
/#missing
4.30 निम्नलिखित अणुओं में कार्बन परमाणु कौन से संकर कक्षक प्रयुक्त करते हैं? (क) $\mathrm{CH} _{3}-\mathrm{CH} _{3}$ (ख) $\mathrm{CH} _{3}-\mathrm{CH}=\mathrm{CH} _{2}$ (ग) $\mathrm{CH} _{3}-\mathrm{CH} _{2}-\mathrm{OH}$ (घ) $\mathrm{CH} _{3} \mathrm{CHO}$ (ड़) $\mathrm{CH} _{3} \mathrm{COOH}$
Show Answer
Answer
/#missing
4.31 इलेक्ट्रॉनों के आबंधी युग्म तथा एकांकी युग्म से आप क्या समझते हैं? प्रत्येक के एक उदाहरण द्वारा स्पष्ट कीजिए।
Show Answer
Answer
/#missing
4.32 सिग्मा तथा पाई आबंध में अंतर स्पष्ट कीजिए।
Show Answer
Answer
/#missing
4.33 संयोजकता आबंध सिद्धांत के आधार पर $\mathrm{H} _{2}$ अणु के विरचन की व्याख्या कीजिए।
Show Answer
Answer
/#missing
4.34 परमाणु कक्षकों के रैखिक संयोग से आण्विक कक्षक बनने के लिए आवश्यक शर्तों कों लिखें।
Show Answer
Answer
/#missing
4.35 आण्विक कक्षक सिद्धांत के आधार पर समझाइए कि $\mathrm{Be} _{2}$ अणु का अस्तित्व क्यों नहीं होता।
Show Answer
Answer
/#missing
4.36 निम्नलिखित स्पीशीज़ के आपेक्षिक स्थायित्व की तुलना कीजिए तथा उनके चुंबकीय गुण इंगित कीजिए-
$\mathrm{O} _{2}, \mathrm{O} _{2}^{+}, \mathrm{O} _{2}^{-}$(सुपर ऑक्साइड) तथा $\mathrm{O} _{2}^{2-}$ (परऑक्साइड)
Show Answer
Answer
/#missing
4.37 कक्षकों के निरूपण में उपयुक्त धन $(+)$ तथा ऋणा (-) चिह्नों का क्या महत्त्व होता है?
Show Answer
Answer
/#missing
4.38 $\mathrm{PCl} _{5}$ अणु में संकरण का वर्णन कीजिए। इसमें अक्षीय आबंध विषुवतीय आबंधों की अपेक्षा अधिक लंबे क्यों होते हैं?
Show Answer
Answer
/#missing
4.39 हाइड्रोजन आबंध की परिभाषा दीजिए। यह वान्डरवाल्स बलों की अपेक्षा प्रबल होते है या दुर्बल?
Show Answer
Answer
/#missing
4.40 ‘आबंध कोटि’ से आप क्या समझते हैं? निम्नलिखित में आबंध-कोटि का परिकलन कीजिए- $ \mathrm{N} _{2}, \mathrm{O} _{2}, \mathrm{O} _{2}^{+} \text {तथा } \mathrm{O} _{2}^{-} $
Show Answer
Answer
/#missing










