Chapter-11 Electricity
Electricity has an important place in modern society. It is a controllable and convenient form of energy for a variety of uses in homes, schools, hospitals, industries and so on. What constitutes electricity? How does it flow in an electric circuit? What are the factors that control or regulate the current through an electric circuit? In this Chapter, we shall attempt to answer such questions. We shall also discuss the heating effect of electric current and its applications.
11.1 ELECTRIC CURRENT AND CIRCUIT
We are familiar with air current and water current. We know that flowing water constitute water current in rivers. Similarly, if the electric charge flows through a conductor (for example, through a metallic wire), we say that there is an electric current in the conductor. In a torch, we know that the cells (or a battery, when placed in proper order) provide flow of charges or an electric current through the torch bulb to glow. We have also seen that the torch gives light only when its switch is on. What does a switch do? A switch makes a conducting link between the cell and the bulb. A continuous and closed path of an electric current is called an electric circuit. Now, if the circuit is broken anywhere (or the switch of the torch is turned off), the current stops flowing and the bulb does not glow.
How do we express electric current? Electric current is expressed by the amount of charge flowing through a particular area in unit time. In other words, it is the rate of flow of electric charges. In circuits using metallic wires, electrons constitute the flow of charges. However, electrons were not known at the time when the phenomenon of electricity was first observed. So, electric current was considered to be the flow of positive charges and the direction of flow of positive charges was taken to be the direction of electric current. Conventionally, in an electric circuit the direction of electric current is taken as opposite to the direction of the flow of electrons, which are negative charges.

Figure 11.1 A schematic diagram of an electric circuit comprising - cell, electric bulb, ammeter and plug key
If a net charge $Q$, flows across any cross-section of a conductor in time $t$, then the current $I$, through the cross-section is
$$ \begin{equation*} I=\dfrac{Q}{t} \tag{11.1} \end{equation*} $$
The SI unit of electric charge is coulomb (C), which is equivalent to the charge contained in nearly $6 \times 10^{18}$ electrons. (We know that an electron possesses a negative charge of $1.6 \times 10^{-19} C$.) The electric current is expressed by a unit called ampere (A), named after the French scientist, Andre-Marie Ampere (1775-1836). One ampere is constituted by the flow of one coulomb of charge per second, that is, $1 A=1 C / 1 s$. Small quantities of current are expressed in milliampere $(1 mA=10^{-3} A)$ or in microampere $(1 \mu A=10^{-6} A)$. An instrument called ammeter measures electric current in a circuit. It is always connected in series in a circuit through which the current is to be measured. Figure 11.1 shows the schematic diagram of a typical electric circuit comprising a cell, an electric bulb, an ammeter and a plug key. Note that the electric current flows in the circuit from the positive terminal of the cell to the negative terminal of the cell through the bulb and ammeter.
Example 11.1
A current of $0.5 A$ is drawn by a filament of an electric bulb for 10 minutes. Find the amount of electric charge that flows through the circuit.
Solution
We are given, $I=0.5 A ; t=10 min=600 s$.
From Eq. (11.1), we have
$$ \begin{aligned} Q & =I t \\ & =0.5 A \times 600 s \\ & =300 C \end{aligned} $$
QUESTIONS
1. What does an electric circuit mean?
Show Answer
Answer
A continuous and closed path of an electric current is called an electric circuit. An electric circuit consists of electric devices, source of electricity and wires that are connected with the help of a switch.
2. Define the unit of current.
Show Answer
Answer
The unit of electric current is ampere (A). $1 A$ is defined as the flow of $1 C$ of charge through a wire in $1 s$.
3. Calculate the number of electrons constituting one coulomb of charge.
Show Answer
Answer
One electron possesses a charge of $1.6 \times 10^{-19} C$, i.e., $1.6 \times 10^{-19} C$ of charge is contained in 1 electron.
$\therefore 1 C$ of charge is contained in $1 / 1.6 \times 10^{-19}=6.25 \times 10^{18}=6 \times 10^{18}$
Therefore, $6 \times 10^{18}$ electrons constitute one coulomb of charge.
11.2 ELECTRIC POTENTIAL AND POTENTIAL DIFFERENCE
What makes the electric charge to flow? Let us consider the analogy of flow of water. Charges do not flow in a copper wire by themselves, just as water in a perfectly horizontal tube does not flow. If one end of the tube is connected to a tank of water kept at a higher level, such that there is a pressure difference between the two ends of the tube, water flows out of the other end of the tube. For flow of charges in a conducting metallic wire, the gravity, of course, has no role to play; the electrons move only if there is a difference of electric pressure - called the potential difference along the conductor. This difference of potential may be produced by a battery, consisting of one or more electric cells. The chemical action within a cell generates the potential difference across the terminals of the cell, even when no current is drawn from it. When the cell is connected to a conducting circuit element, the potential difference sets the charges in motion in the conductor and produces an electric current. In order to maintain the current in a given electric circuit, the cell has to expend its chemical energy stored in it.
We define the electric potential difference between two points in an electric circuit carrying some current as the work done to move a unit charge from one point to the other -
Potential difference $(V)$ between two points $=$ Work done $(W) /$ Charge $(Q)$
$$ \begin{equation*} V=W / Q \tag{11.2} \end{equation*} $$
The SI unit of electric potential difference is volt $(V)$, named after Alessandro Volta (1745-1827), an Italian physicist. One volt is the potential difference between two points in a current carrying conductor when 1 joule of work is done to move a charge of 1 coulomb from one point to the other.
$$ \text{ Therefore, 1 volt } =\dfrac{1 \text{ joule }}{1 \text{ coulomb }}$$
$$ \begin{equation*} 1 \mathrm{~V}=1 \mathrm{JC}^{-1} \tag{11.3} \end{equation*} $$
The potential difference is measured by means of an instrument called the voltmeter. The voltmeter is always connected in parallel across the points between which the potential difference is to be measured.
Example 11.2
How much work is done in moving a charge of $2 C$ across two points having a potential difference $12 V$ ?
Solution
The amount of charge $Q$, that flows between two points at potential difference $V(=12 V)$ is $2 C$. Thus, the amount of work $W$, done in moving the charge [from Eq. (11.2)] is
$$ \begin{matrix} W & = V Q \\ & = 12 V \times 2 C \\ & = 24 J . \end{matrix} $$
QUESTIONS
1. Name a device that helps to maintain a potential difference across a conductor.
Show Answer
Answer
Any source of electricity like battery, cell, power supply, etc. helps to maintain a potential difference across a conductor.
2. What is meant by saying that the potential difference between two points is $1 V$ ?
Show Answer
Answer
If $1 J$ of work is required to move a charge of amount $1 C$ from one point to another, then it is said that the potential difference between the two points is $1 V$.
3. How much energy is given to each coulomb of charge passing through a $6 V$ battery?
Show Answer
Answer
The energy given to each coulomb of charge is equal to the amount of work which is done in moving it.
Now we know that,
Potential difference $=$ Work Done/Charge
$\therefore$ Work done $=$ Potential difference $\times$ charge
Where, Charge $=1 C$ and Potential difference $=6 V$
$\therefore$ Work done $=6 \times 1$
$=6$ Joule.
11.3 CIRCUIT DIAGRAM
We know that an electric circuit, as shown in Fig. 11.1, comprises a cell (or a battery), a plug key, electrical component(s), and connecting wires. It is often convenient to draw a schematic diagram, in which different components of the circuit are represented by the symbols conveniently used. Conventional symbols used to represent some of the most commonly used electrical components are given in Table 11.1.
Table 11.1 Symbols of some commonly used components in circuit diagrams


11.4 OHM’S LAW
Is there a relationship between the potential difference across a conductor and the current through it? Let us explore with an Activity.
Activity 11.1
- Set up a circuit as shown in Fig. 11.2, consisting of a nichrome wire XY of length, say $0.5 m$, an ammeter, a voltmeter and four cells of $1.5 V$ each. (Nichrome is an alloy of nickel, chromium, manganese, and iron metals.)
- First use only one cell as the source in the circuit. Note the reading in the ammeter $I$, for the current and reading of the voltmeter $V$ for the potential difference across the nichrome wire $XY$ in the circuit. Tabulate them in the Table given.

Figure 11.2 Electric circuit for studying Ohm’s law
- Next connect two cells in the circuit and note the respective readings of the ammeter and voltmeter for the values of current through the nichrome wire and potential difference across the nichrome wire.
- Repeat the above steps using three cells and then four cells in the circuit separately.
- Calculate the ratio of $V$ to $I$ for each pair of potential difference $V$ and current $I$.
| S. No. | Number of cells used in the circuit (ampere) | Current through the nichrome wire, $I$ wire, $V$ (volt) | Potential difference across the nichrome | $V / I$ (volt/ampere) |
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 2 | |||
| 3 | 3 | |||
| 4 | 4 |
- Plot a graph between $V$ and $I$, and observe the nature of the graph.

Figure 11.3 $V-I$ graph for a nichrome wire. A straight line plot shows that as the current through a wire increases, the potential difference across the wire increases linearly - this is Ohm’s law.
In this Activity, you will find that approximately the same value for $V / I$ is obtained in each case. Thus the $V-I$ graph is a straight line that passes through the origin of the graph, as shown in Fig. 11.3. Thus, $V / I$ is a constant ratio.
In 1827, a German physicist Georg Simon Ohm (1787-1854) found out the relationship between the current $I$, flowing in a metallic wire and the potential difference across its terminals. The potential difference, $V$, across the ends of a given metallic wire in an electric circuit is directly proportional to the current flowing through it, provided its temperature remains the same. This is called Ohm’s law. In other words -
$ \begin{equation*} V \propto I \tag{11.4} \end{equation*} $
or $\hspace{40 px} V/I = $ constant
$ \hspace{70 px} = R $
or
$ \begin{equation*} \hspace{50 px} V = IR \tag{11.5} \end{equation*} $
In Eq. (11.4), $R$ is a constant for the given metallic wire at a given temperature and is called its resistance. It is the property of a conductor to resist the flow of charges through it. Its SI unit is ohm, represented by the Greek letter $\Omega$. According to Ohm’s law,
$ \begin{equation*} R=V / I \tag{11.6} \end{equation*} $
If the potential difference across the two ends of a conductor is $1 V$ and the current through it is $1 A$, then the resistance $R$, of the conductor is $1 \Omega$. That is,
$1 ohm=\dfrac{1 \text{ volt }}{1 \text{ ampere }}$
Also from Eq. (11.5) we get
$ \begin{equation*} I=V / R \tag{11.7} \end{equation*} $
It is obvious from Eq. (11.7) that the current through a resistor is inversely proportional to its resistance. If the resistance is doubled the current gets halved. In many practical cases it is necessary to increase or decrease the current in an electric circuit. A component used to regulate current without changing the voltage source is called variable resistance. In an electric circuit, a device called rheostat is often used to change the resistance in the circuit. We will now study about electrical resistance of a conductor with the help of following Activity.
Activity 11.2
- Take a nichrome wire, a torch bulb, a $10 W$ bulb and an ammeter ( 0 - 5 A range), a plug key and some connecting wires.
- Set up the circuit by connecting four dry cells of $1.5 V$ each in series with the ammeter leaving a gap XY in the circuit, as shown in Fig. 11.4.

Figure 11.4
- Complete the circuit by connecting the nichrome wire in the gap XY. Plug the key. Note down the ammeter reading. Take out the key from the plug. [Note: Always take out the key from the plug after measuring the current through the circuit.]
- Replace the nichrome wire with the torch bulb in the circuit and find the current through it by measuring the reading of the ammeter.
- Now repeat the above step with the $10 W$ bulb in the gap XY.
- Are the ammeter readings different for different components connected in the gap XY? What do the above observations indicate?
- You may repeat this Activity by keeping any material component in the gap. Observe the ammeter readings in each case. Analyse the observations.
In this Activity we observe that the current is different for different components. Why do they differ? Certain components offer an easy path for the flow of electric current while the others resist the flow. We know that motion of electrons in an electric circuit constitutes an electric current. The electrons, however, are not completely free to move within a conductor. They are restrained by the attraction of the atoms among which they move. Thus, motion of electrons through a conductor is retarded by its resistance. A component of a given size that offers a low resistance is a good conductor. A conductor having some appreciable resistance is called a resistor. A component of identical size that offers a higher resistance is a poor conductor. An insulator of the same size offers even higher resistance.
11.5 FACTORS ON WHICH THE RESISTANCE OF A CONDUCTOR DEPENDS
Activity 11.3
- Complete an electric circuit consisting of a cell, an ammeter, a nichrome wire of length $l$ [say, marked (1)] and a plug key, as shown in Fig. 11.5.

Figure 11.5 Electric circuit to study the factors on which the resistance of conducting wires depends
- Now, plug the key. Note the current in the ammeter.
- Replace the nichrome wire by another nichrome wire of same thickness but twice the length, that is $2 l$ [marked (2) in the Fig. 11.5].
- Note the ammeter reading.
- Now replace the wire by a thicker nichrome wire, of the same length $l$ [marked (3)]. A thicker wire has a larger cross-sectional area. Again note down the current through the circuit.
- Instead of taking a nichrome wire, connect a copper wire [marked (4) in Fig. 11.5] in the circuit. Let the wire be of the same length and same area of cross-section as that of the first nichrome wire [marked (1)]. Note the value of the current.
- Notice the difference in the current in all cases.
- Does the current depend on the length of the conductor?
- Does the current depend on the area of cross-section of the wire used?
It is observed that the ammeter reading decreases to one-half when the length of the wire is doubled. The ammeter reading is increased when a thicker wire of the same material and of the same length is used in the circuit. A change in ammeter reading is observed when a wire of different material of the same length and the same area of cross-section is used. On applying Ohm’s law [Eqs. (11.5) - (11.7)], we observe that the resistance of the conductor depends (i) on its length, (ii) on its area of cross-section, and (iii) on the nature of its material. Precise measurements have shown that resistance of a uniform metallic conductor is directly proportional to its length $(l)$ and inversely proportional to the area of cross-section $(A)$. That is,
$$ \begin{equation*} R \propto l \tag{11.8} \end{equation*} $$
and
$$ \begin{equation*} \mathrm{R} \propto 1 / \mathrm{A} \tag{11.9} \end{equation*} $$
Combining Eqs. (11.8) and (11.9) we get
$$ \begin{aligned} R & \propto \dfrac{l}{A} \\ \text{ or, } \quad R & =\rho \dfrac{l}{A} \qquad \qquad (11.10) \end{aligned} $$
where $\rho$ (rho) is a constant of proportionality and is called the electrical resistivity of the material of the conductor. The SI unit of resistivity is $\Omega m$. It is a characteristic property of the material. The metals and alloys have very low resistivity in the range of $10^{-8} \Omega m$ to $10^{-6} \Omega m$. They are good conductors of electricity. Insulators like rubber and glass have resistivity of the order of $10^{12}$ to $10^{17} \Omega m$. Both the resistance and resistivity of a material vary with temperature.
Table 11.2 reveals that the resistivity of an alloy is generally higher than that of its constituent metals. Alloys do not oxidise (burn) readily at high temperatures. For this reason, they are commonly used in electrical heating devices, like electric iron, toasters etc. Tungsten is used almost exclusively for filaments of electric bulbs, whereas copper and aluminium are generally used for electrical transmission lines.
Table 11.2 Electrical resistivity* of some substances at $20^{\circ} C$
| Material | Resistivity $(\boldsymbol{{}\Omega} \mathbf{~ m})$ | |
|---|---|---|
| Conductors | Silver | $1.60 \times 10^{-8}$ |
| Copper | $1.62 \times 10^{-8}$ | |
| Aluminium | $2.63 \times 10^{-8}$ | |
| Tungsten | $5.20 \times 10^{-8}$ | |
| Nickel | $6.84 \times 10^{-8}$ | |
| Iron | $10.0 \times 10^{-8}$ | |
| Chromium | $12.9 \times 10^{-8}$ | |
| Mercury | $94.0 \times 10^{-8}$ | |
| Manganese | $1.84 \times 10^{-6}$ | |
| Alloys | Constantan | $49 \times 10^{-6}$ |
| (alloy of Cu and Ni) | ||
| Manganin | $44 \times 10^{-6}$ | |
| (alloy of Cu, Mn and Ni) | ||
| Nichrome | $100 \times 10^{-6}$ | |
| (alloy of Ni, Cr, Mn and Fe) | ||
| Insulators | Glass | $10^{10}-10^{14}$ |
| Hard rubber | $10^{13}-10^{16}$ | |
| Ebonite | $10^{15}-10^{17}$ | |
| Diamond | $10^{12}-10^{13}$ | |
| Paper (Dry) | $10^{12}$ |
- You need not memorise these values. You can use these values for solving numerical problems.
Example 11.3
(a) How much current will an electric bulb draw from a $220 V$ source, if the resistance of the bulb filament is $1200 \Omega$ ? (b) How much current will an electric heater coil draw from a $220 V$ source, if the resistance of the heater coil is $100 \Omega$ ?
Solution
(a) We are given $V=220 V ; R=1200 \Omega$.
From Eq. (12.6), we have the current $I=220 V / 1200 \Omega=0.18 A$.
(b) We are given, $V=220 V, R=100 \Omega$.
From Eq. (11.6), we have the current $I=220 V / 100 \Omega=2.2 A$.
Note the difference of current drawn by an electric bulb and electric heater from the same $220 V$ source!
Example 11.4
The potential difference between the terminals of an electric heater is $60 V$ when it draws a current of $4 A$ from the source. What current will the heater draw if the potential difference is increased to $120 V$ ? Solution
Solution
We are given, potential difference $V=60 V$, current $I=4$ A.
According to Ohm’s law, $R=\dfrac{V}{I}=\dfrac{60 V}{4 A}=15 \Omega$.
When the potential difference is increased to $120 V$ the current is given by
current $=\dfrac{V}{R}=\dfrac{120 V}{15 \Omega}=8 A$.
The current through the heater becomes $8 A$.
Example 11.5
Resistance of a metal wire of length $1 m$ is $26 \Omega$ at $20^{\circ} C$. If the diameter of the wire is $0.3 mm$, what will be the resistivity of the metal at that temperature? Using Table 11.2, predict the material of the wire.
Solution
We are given the resistance $R$ of the wire $=26 \Omega$, the diameter $d=0.3 mm=3 \times 10^{-4} m$, and the length $l$ of the wire $=1 m$.
Therefore, from Eq. (11.10), the resistivity of the given metallic wire is
$\rho=(R A / l)=(R \pi d^{2} / 4 l)$
Substitution of values in this gives
$\rho=1.84 \times 10^{-6} \Omega m$
The resistivity of the metal at $20^{\circ} C$ is $1.84 \times 10^{-6} \Omega m$. From Table 11.2, we see that this is the resistivity of manganese.
Example 11.6
A wire of given material having length $l$ and area of cross-section $A$ has a resistance of $4 \Omega$. What would be the resistance of another wire of the same material having length $l / 2$ and area of cross-section $2 A$ ?
Solution
For first wire
$ R_1=\rho \dfrac{l}{A}=4 \Omega $
Now for second wire
$R_2=\rho \dfrac{l / 2}{2 A}=\dfrac{1}{4} \rho \dfrac{l}{A}$
$R_2=\dfrac{1}{4} \quad R_1$
$R_2=1 \Omega$
The resistance of the new wire is $1 \Omega$.
QUESTIONS
1. On what factors does the resistance of a conductor depend?
Show Answer
Answer
The resistance of a conductor depends upon the following factors:
$\rightarrow$ Length of the conductor
$\rightarrow$ Cross-sectional area of the conductor
$\rightarrow$ Material of the conductor
$\rightarrow$ Temperature of the conductor
2. Will current flow more easily through a thick wire or a thin wire of the same material, when connected to the same source? Why?
Show Answer
Answer
The current will flow more easily through thick wire. It is because the resistance of a conductor is inversely proportional to its area of cross - section. If thicker the wire, less is resistance and hence more easily the current flows.
3. Let the resistance of an electrical component remains constant while the potential difference across the two ends of the component decreases to half of its former value. What change will occur in the current through it?
Show Answer
Answer
According to Ohm’s law
$V=I R$ $\Rightarrow I=V / R \ldots$
Now Potential difference is decreased to half
$\therefore$ New potential difference $V^{\prime}=V / 2$
Resistance remains constant
So the new current $I^{\prime}=V^{\prime} / R$
$=(V / 2) / R$
$=(1 / 2)(V / R)$
$=(1 / 2) I=I / 2$
Therefore, the amount of current flowing through the electrical component is reduced by half.
4. Why are coils of electric toasters and electric irons made of an alloy rather than a pure metal?
Show Answer
Answer
The resistivity of an alloy is higher than the pure metal. Moreover, at high temperatures, the alloys do not melt readily. Hence, the coils of heating appliances such as electric toasters and electric irons are made of an alloy rather than a pure metal.
5. Use the data in Table 11.2 to answer the following –
(a) Which among iron and mercury is a better conductor?
(b) Which material is the best conductor?
Show Answer
Answer
Table 12.2 Electrical resistivity of some substances at $20^{\circ} C$
| - | Material | Resistivity $(\Omega m)$ |
|---|---|---|
| Conductors | Silver | $1.60 \times 10^{-8}$ |
| Copper | $1.62 \times 10^{-8}$ | |
| Aluminium | $2.63 \times 10^{-8}$ | |
| Tungsten | $5.20 \times 10^{-8}$ | |
| Nickel | $6.84 \times 10^{-8}$ | |
| Iron | $10.0 \times 10^{-8}$ | |
| Chromium | $12.9 \times 10^{-8}$ | |
| Mercury | $1.84 \times 10^{-6}$ | |
| Manganese | $49 \times 10^{-6}$ | |
| Constantan (alloy of Cu and Ni) |
||
| Alloys | Manganin (alloy of Cu, Mn and Ni) |
$44 \times 10^{-6}$ |
| :— | :— | :— |
| Nichrome (alloy of Ni, Cr, Mn and Fe) |
$100 \times 10^{-6}$ | |
| Glass | $10^{10}-10^{14}$ | |
| Insulators | Hard rubber | $10^{13}-10^{16}$ |
| Ebonite | $10^{15}-10^{17}$ | |
| Diamond | $10^{12}-10^{13}$ | |
| Paper (dry) | $10^{12}$ |
(a) Resistivity of iron $=10.0 \times 10^{-8} \Omega$
Resistivity of mercury $=94.0 \times 10^{-8} \Omega$
Resistivity of mercury is more than that of iron. This implies that iron is a better conductor than mercury.
(b) It can be observed from Table 12.2 that the resistivity of silver is the lowest among the listed materials. Hence, it is the best conductor.
11.6 RESISTANCE OF A SYSTEM OF RESISTORS
In preceding sections, we learnt about some simple electric circuits. We have noticed how the current through a conductor depends upon its resistance and the potential difference across its ends. In various electrical gadgets, we often use resistors in various combinations. We now therefore intend to see how Ohm’s law can be applied to combinations of resistors.
There are two methods of joining the resistors together. Figure 11.6 shows an electric circuit in which three resistors having resistances $R_1$, $R_2$ and $R_3$, respectively, are joined end to end. Here the resistors are said to be connected in series.

Figure 11.6 Resistors in series
Figure 11.7 shows a combination of resistors in which three resistors are connected together between points $X$ and $Y$. Here, the resistors are said to be connected in parallel.

Figure 11.7 Resistors in parallel
11.6.1 Resistors in Series
What happens to the value of current when a number of resistors are connected in series in a circuit? What would be their equivalent resistance? Let us try to understand these with the help of the following activities.
Activity 11.4
- Join three resistors of different values in series. Connect them with a battery, an ammeter and a plug key, as shown in Fig. 11.6. You may use the resistors of values like $1 \Omega, 2 \Omega, 3 \Omega$ etc., and a battery of $6 V$ for performing this Activity.
- Plug the key. Note the ammeter reading.
- Change the position of ammeter to anywhere in between the resistors. Note the ammeter reading each time.
- Do you find any change in the value of current through the ammeter?
You will observe that the value of the current in the ammeter is the same, independent of its position in the electric circuit. It means that in a series combination of resistors the current is the same in every part of the circuit or the same current through each resistor.
Activity 11.5
- In Activity 11.4, insert a voltmeter across the ends $X$ and $Y$ of the series combination of three resistors, as shown in Fig. 11.6.
- Plug the key in the circuit and note the voltmeter reading. It gives the potential difference across the series combination of resistors. Let it be $V$. Now measure the potential difference across the two terminals of the battery. Compare the two values.
- Take out the plug key and disconnect the voltmeter. Now insert the voltmeter across the ends $X$ and $P$ of the first resistor, as shown in Fig. 11.8.
- Plug the key and measure the potential difference across the first resistor. Let it be $V_1$.
- Similarly, measure the potential difference across the other two resistors, separately. Let these values be $V_2$ and $V_3$, respectively.
- Deduce a relationship between $V, V_1, V_2$ and $V_3$.

Figure 11.8
You will observe that the potential difference $V$ is equal to the sum of potential differences $V_1, V_2$, and $V_3$. That is the total potential difference across a combination of resistors in series is equal to the sum of potential difference across the individual resistors. That is,
$$ \begin{equation*} V=V _{1}+V _{2}+V _{3} \tag{11.11} \end{equation*} $$
In the electric circuit shown in Fig. 11.8 , let $I$ be the current through the circuit. The current through each resistor is also $I$. It is possible to replace the three resistors joined in series by an equivalent single resistor of resistance $R$, such that the potential difference $V$ across it, and the current I through the circuit remains the same. Applying the Ohm’s law to the entire circuit, we have
$$ \begin{equation*} V=I R \tag{11.12} \end{equation*} $$
On applying Ohm’s law to the three resistors separately, we further have
$$ \begin{align*} & V _{1}=I R _{1} \tag{11.13a} \\ & V _{2}=I R _{2} \tag{11.13b} \\ \text {and} & V _{3}=I R _{3} \tag{11.13c} \end{align*} $$
From Eq. (11.11),
$$ I R=I R _{1}+I R _{2}+I R _{3} $$
or
$$ \begin{equation*} R s=R _{1}+R _{2}+R _{3} \tag{11.14} \end{equation*} $$
We can conclude that when several resistors are joined in series, the resistance of the combination $R_s$ equals the sum of their individual resistances, $R_1, R_2, R_3$, and is thus greater than any individual resistance.
Example 11.7
An electric lamp, whose resistance is $20 \Omega$, and a conductor of $4 \Omega$ resistance are connected to a $6 V$ battery (Fig. 11.9). Calculate (a) the total resistance of the circuit, (b) the current through the circuit, and (c) the potential difference across the electric lamp and conductor.

Figure 11.9 An electric lamp connected in series with a resistor of $4 \Omega$ to a $6 V$ battery
Solution
The resistance of electric lamp, $R_1=20 \Omega$,
The resistance of the conductor connected in series, $R_2=4 \Omega$.
Then the total resistance in the circuit
$R=R_1+R_2$
$R_s=20 \Omega+4 \Omega=24 \Omega$.
The total potential difference across the two terminals of the battery $V=6 V$.
Now by Ohm’s law, the current through the circuit is given by
$$ \begin{aligned} I & =V / R_s \\ & =6 V / 24 \Omega \\ & =0.25 A . \end{aligned} $$
Applying Ohm’s law to the electric lamp and conductor separately, we get potential difference across the electric lamp,
$V_1=20 \Omega \times 0.25 A$
$=5 V$
and,
that across the conductor, $V_2=4 \Omega \times 0.25 A = 1 V$.
Suppose that we like to replace the series combination of electric lamp and conductor by a single and equivalent resistor. Its resistance must be such that a potential difference of $6 V$ across the battery terminals will cause a current of $0.25 A$ in the circuit. The resistance $R$ of this equivalent resistor would be
$$ \begin{aligned} R & =V / I \\ & =6 V / 0.25 A \\ & =24 \Omega . \end{aligned} $$
This is the total resistance of the series circuit; it is equal to the sum of the two resistances.
QUESTIONS
1. Draw a schematic diagram of a circuit consisting of a battery of three cells of $2 V$ each, a $5 \Omega$ resistor, an $8 \Omega$ resistor, and a $12 \Omega$ resistor, and a plug key, all connected in series.
Show Answer
Answer
Three cells of potential $2 V$, each connected in series therefore the potential difference of the battery will be $2 V+2 V+2 V=6 V$. The following circuit diagram shows three resistors of resistances $5 \Omega, 8 \Omega$ and $12 \Omega$ respectively connected in series and a battery of potential $6 V$ and a plug key which is closed means the current is flowing in the circuit.

2. Redraw the circuit of Question 1, putting in an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the $12 \Omega$ resistor. What would be the readings in the ammeter and the voltmeter?
Show Answer
Answer
An ammeter should be connected in the circuit in series with the resistors. To measure the potential difference across the resistor it should be connected in parallel, as shown in the following figure.

The resistances are connected in series.
Ohm’s law can be used to obtain the readings of ammeter and voltmeter. According to Ohm’s law,
$V=I R$,
Where,
Potential difference, $V=6 V$
Current flowing through the circuit/resistors $=I$
Resistance of the circuit, $R=5+8+12=25 \Omega$
$I=V / R=6 / 25=0.24 A$
Potential difference across $12 \Omega$ resistor $=V_1$
Current flowing through the $12 \Omega$ resistor, $I=0.24 A$
Therefore, using Ohm’s law, we obtain
$V_1=I R=0.24 \times 12=2.88 V$
Therefore, the reading of the ammeter will be $0.24 A$.
The reading of the voltmeter will be $2.88 V$.
11.6.2 Resistors in Parallel
Now, let us consider the arrangement of three resistors joined in parallel with a combination of cells (or a battery), as shown in Fig.11.7.

Figure 11.10
Activity 11.6
- Make a parallel combination, XY, of three resistors having resistances $R_1, R_2$, and $R_3$, respectively. Connect it with a battery, a plug key and an ammeter, as shown in Fig. 11.10. Also connect a voltmeter in parallel with the combination of resistors.
- Plug the key and note the ammeter reading. Let the current be $I$. Also take the voltmeter reading. It gives the potential difference $V$, across the combination. The potential difference across each resistor is also $V$. This can be checked by connecting the voltmeter across each individual resistor (see Fig. 11.11).
- Take out the plug from the key. Remove the ammeter and voltmeter from the circuit. Insert the ammeter in series with the resistor $R_1$, as shown in Fig. 11.11. Note the ammeter reading, $I_1$.

Figure 11.11
- Similarly, measure the currents through $R_2$ and $R_3$. Let these be $I_2$ and $I_3$, respectively. What is the relationship between $I, I_1, I_2$ and $I_3$ ?
It is observed that the total current $I$, is equal to the sum of the separate currents through each branch of the combination.
$I=I_1+I_2+I_3$
Let $R_p$ be the equivalent resistance of the parallel combination of resistors. By applying Ohm’s law to the parallel combination of resistors, we have
$I=V / R_p$
On applying Ohm’s law to each resistor, we have
$I_1=V / R_1 ; \quad I_2=V / R_2 ;$ and $I_3=V / R_3$
From Eqs. (11.15) to (11.17), we have
$ V / R_p=V / R_1+V / R_2+V / R_3 $
or
$ \begin{equation*} 1 / R _{p}=1 / R _{1}+1 / R _{2}+1 / R _{3} \tag{11.18} \end{equation*} $
Thus, we may conclude that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances.
Example 11.8
In the circuit diagram given in Fig. 11.10, suppose the resistors $R_1$, $R_2$ and $R_3$ have the values $5 \Omega, 10 \Omega, 30 \Omega$, respectively, which have been connected to a battery of $12 V$. Calculate (a) the current through each resistor, (b) the total current in the circuit, and (c) the total circuit resistance.
Solution
$R_1=5 \Omega, R_2=10 \Omega$, and $R_3=30 \Omega$.
Potential difference across the battery, $V=12 V$.
This is also the potential difference across each of the individual resistor; therefore, to calculate the current in the resistors, we use Ohm’s law.
The current $I_1$, through $R_1=\quad V / R_1$
$ I_1=12 V / 5 \Omega=2.4 A . $
The current $I_2$, through $R_2=V / R_2$
$ I_2=12 V / 10 \Omega=1.2 A . $
The current $I_3$, through $R_3=V / R_3$
$ I_3=12 V / 30 \Omega=0.4 A . $
The total current in the circuit,
$ \begin{aligned} I & =I_1+I_2+I_3 \\ & =(2.4+1.2+0.4) A \\ & =4 A \end{aligned} $
The total resistance $R_p$, is given by [Eq. (11.18)]
$\dfrac{1}{R_p}=\dfrac{1}{5}+\dfrac{1}{10}+\dfrac{1}{30}=\dfrac{1}{3}$
Thus, $R_p=3 \Omega$.
Example 11.9
If in Fig. 11.12, $R_1=10 \Omega, R_2=40 \Omega, R_3=30 \Omega, R_4=20 \Omega, R_5=60 \Omega$, and a $12 V$ battery is connected to the arrangement. Calculate (a) the total resistance in the circuit, and (b) the total current flowing in the circuit.
Solution
Suppose we replace the parallel resistors $R_1$ and $R_2$ by an equivalent resistor of resistance, $R^{\prime}$. Similarly we replace the parallel resistors $R_3, R_4$ and $R_5$ by an equivalent single resistor of resistance $R^{\prime \prime}$. Then using Eq. (11.18), we have $1 / R^{\prime}=1 / 10+1 / 40=5 / 40$; that is $R^{\prime}=8 \Omega$.
Similarly, $\quad 1 / R^{\prime \prime}=1 / 30+1 / 20+1 / 60=6 / 60 ;$
that is, $R^{\prime \prime}=10 \Omega$.
Thus, the total resistance, $R=R^{\prime}+R^{\prime \prime}=18 \Omega$.
To calculate the current, we use Ohm’s law, and get $I=V / R=12 V / 18 \Omega=0.67 A$.
We have seen that in a series circuit the current is constant throughout the electric circuit. Thus it is obviously impracticable to connect an electric bulb and an electric heater in series, because they need currents of widely different values to operate properly (see Example 11 .3). Another major disadvantage of a series circuit is that when one component fails the circuit is broken and none of the components works. If you have used ‘fairy lights’ to decorate buildings on festivals, on marriage celebrations etc., you might have seen the electrician spending lot of time in trouble-locating and replacing the ‘dead’ bulb - each has to be tested to find which has fused or gone. On the other hand, a parallel circuit divides the current through the electrical gadgets. The total resistance in a parallel circuit is decreased as per Eq. (11.18). This is helpful particularly when each gadget has different resistance and requires different current to operate properly.

Figure 11.12 An electric circuit showing the combination of series and parallel resistors
QUESTIONS
1. Judge the equivalent resistance when the following are connected in parallel - (a) $1 \Omega$ and $10^{6} \Omega$, (b) $1 \Omega$ and $10^{3} \Omega$, and $10^{6} \Omega$.
Show Answer
Answer
(a) When $1 \Omega$ and $10^{6} \Omega$ are connected in parallel:
Let $R$ be the equivalent resistance.
$ \begin{aligned} & \therefore \dfrac{1}{R}=\dfrac{1}{1}+\dfrac{1}{10^{6}} \\ & R=\dfrac{10^{6}}{1+10^{6}} \approx \dfrac{10^{6}}{10^{6}}=1 \Omega \end{aligned} $
Therefore, equivalent resistance $\approx 1 \Omega$
(b) When $1 \Omega, 103 \Omega$ and $106 \Omega$ are connected in parallel:
Let $R$ be the equivalent resistance.
$ \begin{aligned} & \dfrac{1}{R}=\dfrac{1}{1}+\dfrac{1}{10^{3}}+\dfrac{1}{10^{6}} \dfrac{10^{6}+10^{3}+1}{10^{6}} \\ & R=\dfrac{1000000}{1001001}=0.999 \Omega \end{aligned} $
Therefore, equivalent resistance $=0.999 \Omega$
2. An electric lamp of $100 \Omega$, a toaster of resistance $50 \Omega$, and a water filter of resistance $500 \Omega$ are connected in parallel to a $220 V$ source. What is the resistance of an electric iron connected to the same source that takes as much current as all three appliances, and what is the current through it?
Show Answer
Answer
Resistance of electric lamp, $R_1=100 \Omega$
Resistance of toaster, $R_2=50 \Omega$
Resistance of water filter, $R_3=500 \Omega$
Potential difference of the source, $V=220 V$
These are connected in parallel, as shown in the following figure. $R_1=100 \Omega$
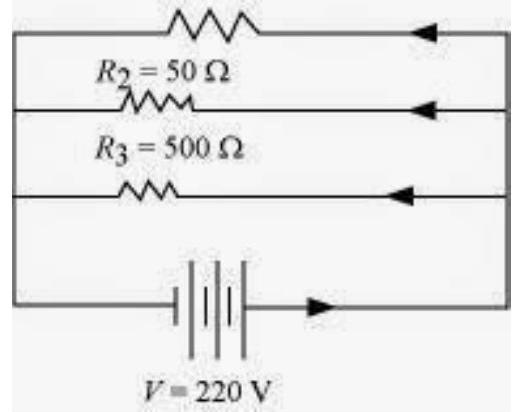
Let $R$ be the equivalent resistance of the circuit. $\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{100}+\dfrac{1}{50}+\dfrac{1}{500}$
According to Ohm’s law,
$V=I R$
$I=\dfrac{V}{R}$
Where,
Current flowing through the circuit $=I$
$I=\dfrac{220}{\dfrac{500}{16}}=\dfrac{220 / 16}{50}=7.04 A$
7.04 A of current is drawn by all the three given appliances.
Therefore, current drawn by an electric iron connected to the same source of potential $220 V=7.04 A$
Let $R^{\prime}$ be the resistance of the electric iron. According to Ohm’s law,
$V=I R^{\prime}$
$R^{\prime}=\dfrac{V}{I}=\dfrac{220}{7.04}=31.25 \Omega$
Therefore, the resistance of the electric iron is $31.25 \Omega$ and the current flowing through it is $7.04 A$.
3. What are the advantages of connecting electrical devices in parallel with the battery instead of connecting them in series?
Show Answer
Answer
There is no division of voltage among the appliances when connected in parallel. The potential difference across each appliance is equal to the supplied voltage.
The total effective resistance of the circuit can be reduced by connecting electrical appliances in parallel.
4. How can three resistors of resistances $2 \Omega, 3 \Omega$, and $6 \Omega$ be connected to give a total resistance of (a) $4 \Omega$, (b) $1 \Omega$ ?
Show Answer
Answer
There are three resistors of resistances $2 \Omega, 3 \Omega$, and $6 \Omega$ respectively.
(a) The following circuit diagram shows the connection of the three resistors.
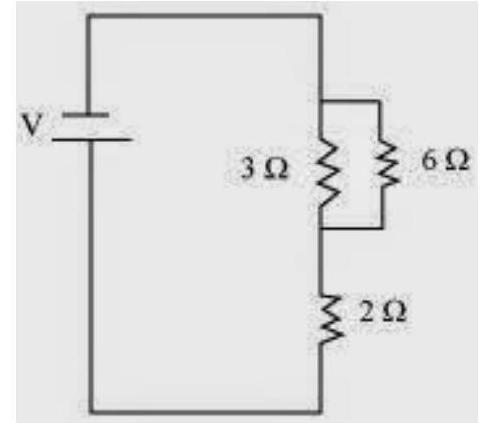
Here, $6 \Omega$ and $3 \Omega$ resistors are connected in parallel.
Therefore, their equivalent resistance will be given by
$ \dfrac{1}{\dfrac{1}{6}+\dfrac{1}{3}}=\dfrac{6 \times 3}{6+3}=2 \Omega $
This equivalent resistor of resistance $2 \Omega$ is connected to a $2 \Omega$ resistor in series.
Therefore, the equivalent resistance of the circuit $=2 \Omega+2 \Omega=4 \Omega$
Hence the total resistance of the circuit is $4 \Omega$.
(b) The following circuit diagram shows the connection of the three resistors.
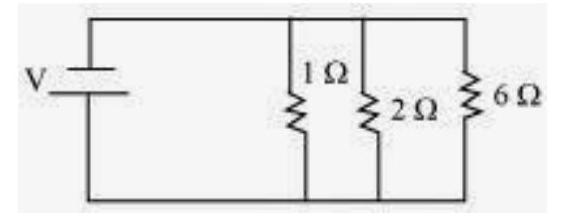
All the resistors are connected in series. Therefore, their equivalent resistance will be given as
$ \dfrac{1}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}}=\dfrac{1}{\dfrac{3+2+1}{6}}=\dfrac{6}{6}=1 \Omega $
Therefore, the total resistance of the circuit is $1 \Omega$.
5. What is (a) the highest, (b) the lowest total resistance that can be secured by combinations of four coils of resistance $4 \Omega, 8 \Omega, 12 \Omega, 24 \Omega$ ?
Show Answer
Answer
There are four coils of resistances $4 \Omega, 8 \Omega, 12 \Omega$ and $24 \Omega$ respectively.
(a) If these coils are connected in series, then the equivalent resistance will be the highest, given by the sum $4+8+12+24=48 \Omega$
(b) If these coils are connected in parallel, then the equivalent resistance will be the lowest, given by
$ \dfrac{1}{\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{12}+\dfrac{1}{24}}=\dfrac{1}{\dfrac{6+3+2+1}{24}}=\dfrac{24}{12}=2 \Omega $
Therefore, $2 \Omega$ is the lowest total resistance.
11.7 HEATING EFFECT OF ELECTRIC CURRENT
We know that a battery or a cell is a source of electrical energy. The chemical reaction within the cell generates the potential difference between its two terminals that sets the electrons in motion to flow the current through a resistor or a system of resistors connected to the battery. We have also seen, in Section 11.2, that to maintain the current, the source has to keep expending its energy. Where does this energy go? A part of the source energy in maintaining the current may be consumed into useful work (like in rotating the blades of an electric fan). Rest of the source energy may be expended in heat to raise the temperature of gadget. We often observe this in our everyday life. For example, an electric fan becomes warm if used continuously for longer time etc. On the other hand, if the electric circuit is purely resistive, that is, a configuration of resistors only connected to a battery; the source energy continually gets dissipated entirely in the form of heat. This is known as the heating effect of electric current. This effect is utilised in devices such as electric heater, electric iron etc.
Consider a current $I$ flowing through a resistor of resistance $R$. Let the potential difference across it be $V$ (Fig. 11.13). Let $t$ be the time during which a charge $Q$ flows across. The work done in moving the charge $Q$ through a potential difference $V$ is $V Q$. Therefore, the source must supply energy equal to $V Q$ in time $t$. Hence the power input to the circuit by the source is
$ \begin{equation*} P=V \dfrac{Q}{t}=V I \tag{11.19} \end{equation*} $
Or the energy supplied to the circuit by the source in time $t$ is $P \times t$, that is, VIt. What happens to this energy expended by the source? This energy gets dissipated in the resistor as heat. Thus for a steady current $I$, the amount of heat $H$ produced in time $t$ is
$ \begin{equation*} H=V I t \tag{11.20} \end{equation*} $
Applying Ohm’s law [Eq. (11.5)], we get
$ \begin{equation*} H=I^{2} R t \tag{11.21} \end{equation*} $
This is known as Joule’s law of heating. The law implies that heat produced in a resistor is (i) directly proportional to the square of current for a given resistance, (ii) directly proportional to resistance for a given current, and (iii) directly proportional to the time for which the current flows through the resistor. In practical situations, when an electric appliance is connected to a known voltage source, Eq. (11.21) is used after calculating the current through it, using the relation $I=V / R$.

Figure 11.13 A steady current in a purely resistive electric circuit
Example 11.10
An electric iron consumes energy at a rate of $840 W$ when heating is at the maximum rate and $360 W$ when the heating is at the minimum. The voltage is $220 V$. What are the current and the resistance in each case?
Solution
From Eq. (11.19), we know that the power input is
$P=V I$
Thus the current $I=P / V$
(a) When heating is at the maximum rate,
$I=840 W / 220 V=3.82 A$;
and the resistance of the electric iron is
$R=V / I=220 V / 3.82 A=57.60 \Omega$.
(b) When heating is at the minimum rate,
$I=360 W / 220 V=1.64 A$;
and the resistance of the electric iron is
$R=V / I=220 V / 1.64 A=134.15 \Omega$.
Example 11.11
$100 J$ of heat is produced each second in a $4 \Omega$ resistance. Find the potential difference across the resistor.
Solution
$H=100 J, R=4 \Omega, t=1 s, V=$ ?
From Eq. (11.21) we have the current through the resistor as
$I=\sqrt{ }(\mathrm{H} / \mathrm{Rt})$
$=\quad \sqrt{ }[100 \mathrm{~J} /(4 \Omega \times 1 \mathrm{~s})]$
$=\quad 5 \mathrm{~A}$
Thus the potential difference across the resistor, $V$ [from Eq. (11.5)] is
$ \begin{aligned} V & =I R \\ & =5 A \times 4 \Omega \\ & =20 V . \end{aligned} $
QUESTIONS
1. Why does the cord of an electric heater not glow while the heating element does?
Show Answer
Answer
The heating element of the heater is made up of alloy which has very high resistance so when current flows through the heating element, it becomes too hot and glows red. But the resistance of cord which is usually of copper or aluminium is very law so it does not glow.
2. Compute the heat generated while transferring 96000 coulomb of charge in one hour through a potential difference of $50 V$.
Show Answer
Answer
Given Charge, $Q=96000 C$
Time, $t=1 hr=60 \times 60=3600 s$
Potential difference, $V=50$ volts
Now we know that $H=$ VIt
So we have to calculate / first
As $l=Q / t$
$\therefore I=96000 / 3600=80 / 3 A$
$ H=50 \times \dfrac{80}{3} \times 60 \times 60=4.8 \times 10^{6} J $
Therefore, the heat generated is $4.8 \times 10^{6} J$.
3. An electric iron of resistance $20 \Omega$ takes a current of $5 A$. Calculate the heat developed in $30 s$.
Show Answer
Answer
The amount of heat $(H)$ produced is given by the joule’s law of heating as $H=Vlt$ Where, Current, $I=5 A$
Time, $t=30 s$
Voltage, $V=$ Current $\times$ Resistance $=5 \times 20=100 V$
$H=100 \times 5 \times 30=1.5 \times 10^{4} J$.
Therefore, the amount of heat developed in the electric iron is $1.5 \times 10^{4} J$.
11.7.1 Practical Applications of Heating Effect of Electric Current
The generation of heat in a conductor is an inevitable consequence of electric current. In many cases, it is undesirable as it converts useful electrical energy into heat. In electric circuits, the unavoidable heating can increase the temperature of the components and alter their properties. However, heating effect of electric current has many useful applications. The electric laundry iron, electric toaster, electric oven, electric kettle and electric heater are some of the familiar devices based on Joule’s heating.
The electric heating is also used to produce light, as in an electric bulb. Here, the filament must retain as much of the heat generated as is possible, so that it gets very hot and emits light. It must not melt at such high temperature. A strong metal with high melting point such as tungsten (melting point $3380^{\circ} C$ ) is used for making bulb filaments. The filament should be thermally isolated as much as possible, using insulating support, etc. The bulbs are usually filled with chemically inactive nitrogen and argon gases to prolong the life of filament. Most of the power consumed by the filament appears as heat, but a small part of it is in the form of light radiated.
Another common application of Joule’s heating is the fuse used in electric circuits. It protects circuits and appliances by stopping the flow of any unduly high electric current. The fuse is placed in series with the device. It consists of a piece of wire made of a metal or an alloy of appropriate melting point, for example aluminium, copper, iron, lead etc. If a current larger than the specified value flows through the circuit, the temperature of the fuse wire increases. This melts the fuse wire and breaks the circuit. The fuse wire is usually encased in a cartridge of porcelain or similar material with metal ends. The fuses used for domestic purposes are rated as $1 A, 2 A, 3 A, 5 A, 10 A$, etc. For an electric iron which consumes $1 kW$ electric power when operated at $220 V$, a current of (1000/220) A, that is, $4.54 A$ will flow in the circuit. In this case, a $5 A$ fuse must be used.
11.8 ELECTRIC POWER
You have studied in your earlier Class that the rate of doing work is power. This is also the rate of consumption of energy.
Equation (11.21) gives the rate at which electric energy is dissipated or consumed in an electric circuit. This is also termed as electric power. The power $P$ is given by
$ \begin{aligned} & P=V I \\ \text{ Or } & P=I^{2} R=V^{2} / R \end{aligned} $
The SI unit of electric power is watt (W). It is the power consumed by a device that carries $1 A$ of current when operated at a potential difference of $1 V$. Thus,
$ 1 W=1 \text{ volt } \times 1 \text{ ampere }=1 V A $
The unit ‘watt’ is very small. Therefore, in actual practice we use a much larger unit called ‘kilowatt’. It is equal to 1000 watts. Since electrical energy is the product of power and time, the unit of electric energy is, therefore, watt hour (W h). One watt hour is the energy consumed when 1 watt of power is used for 1 hour. The commercial unit of electric energy is kilowatt hour (kW h), commonly known as ‘unit’.
$1 kWh=1000$ watt $\times 3600$ second
$=3.6 \times 10^{6}$ watt second
$=3.6 \times 10^{6}$ joule $(J)$
More to know!
Many people think that electron are consumed in a electric circuit. This is wrong! We pay the electricity board or electric company to provide energy to move electrons through the electric gadgets like electric bulb, fan and engines. We pay fir the energy that we use.
Example 11.12
An electric bulb is connected to a $220 V$ generator. The current is $0.50 A$. What is the power of the bulb?
Solution
$ \begin{aligned} P & =V I \\ & =220 V \times 0.50 A \\ & =110 J / s \\ & =110 W . \end{aligned} $
Example 11.13
An electric refrigerator rated $400 W$ operates 8 hour/day. What is the cost of the energy to operate it for 30 days at Rs 3.00 per $kWh$ ?
Solution
The total energy consumed by the refrigerator in 30 days would be
$400 W \times 8.0$ hour $/$ day $\times 30$ days $=96000 W h$
$=96 kWh$
Thus the cost of energy to operate the refrigerator for 30 days is $96 kW h \times$ Rs 3.00 per $kWh=$ Rs 288.00
QUESTIONS
1. What determines the rate at which energy is delivered by a current?
Show Answer
Answer
The rate of consumption of electric energy in an electric appliance is called electric power. Hence, the rate at which energy is delivered by a current is the power of the appliance.
2. An electric motor takes 5 A from a 220 V line. Determine the power of the motor and the energy consumed in $2 h$.
Show Answer
Answer
Power $(P)$ is given by the expression, $P=V I$
Where,
Voltage, $V=220 V$
Current, $I=5 A$
$P=220 \times 5=1100 W$
Energy consumed by the motor $=Pt$
Where,
Time, $t=2 h=2 \times 60 \times 60=7200 s$
$\therefore P=1100 \times 7200=7.92 \times 10^{6} J$
Therefore, power of the motor $=1100 W$
Energy consumed by the motor $=7.92 \times 10^{6} J$
What you have learnt
- A stream of electrons moving through a conductor constitutes an electric current. Conventionally, the direction of current is taken opposite to the direction of flow of electrons.
- The SI unit of electric current is ampere.
- To set the electrons in motion in an electric circuit, we use a cell or a battery. A cell generates a potential difference across its terminals. It is measured in volts (V).
- Resistance is a property that resists the flow of electrons in a conductor. It controls the magnitude of the current. The SI unit of resistance is ohm $(\Omega)$.
- Ohm’s law: The potential difference across the ends of a resistor is directly proportional to the current through it, provided its temperature remains the same.
- The resistance of a conductor depends directly on its length, inversely on its area of cross-section, and also on the material of the conductor.
- The equivalent resistance of several resistors in series is equal to the sum of their individual resistances.
- A set of resistors connected in parallel has an equivalent resistance $R_p$ given by $\dfrac{1}{R_p}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}+\ldots$
- The electrical energy dissipated in a resistor is given by $W=V \times I \times t$
- The unit of power is watt (W). One watt of power is consumed when $1 A$ of current flows at a potential difference of $1 V$.
- The commercial unit of electrical energy is kilowatt hour (kWh). $1 kWh=3,600,000 J=3.6 \times 10^{6} J$.
EXERCISES
1. A piece of wire of resistance $R$ is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is $R^{\prime}$, then the ratio $R / R^{\prime}$ is -
(a) $1 / 25$
(b) $1 / 5$
(c) $5$
(d) $25$
Show Answer
Answer
(d) 25
2. Which of the following terms does not represent electrical power in a circuit?
(a) $I^{2} R$
(b) $I R^{2}$
(c) $V I$
(d) $V^{2} / R$
Show Answer
Answer
(b) $I R^{2}$
3. An electric bulb is rated $220 V$ and $100 W$. When it is operated on $110 V$, the power consumed will be -
(a) $100 W$
(b) $75 W$
(c) $50 W$
(d) $25 W$
Show Answer
Answer
(d) $25 W$
4. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be -
(a) $1: 2$
(b) $2: 1$
(c) $1: 4$
(d) $4: 1$
Show Answer
Answer
(c) $1: 4$
5. How is a voltmeter connected in the circuit to measure the potential difference between two points?
Show Answer
Answer
To measure the potential difference between two points, a voltmeter should be connected in parallel to the points.
6. A copper wire has diameter $0.5 mm$ and resistivity of $1.6 \times 10^{-8} \Omega m$. What will be the length of this wire to make its resistance $10 \Omega$ ? How much does the resistance change if the diameter is doubled?
Show Answer
Answer
Area of cross-section of the wire, $A=\pi(d / 2) 2$
Diameter $=0.5 mm=0.0005 m$
Resistance, $R=10 \Omega$
We know that $R=\rho_A^{l}$
$l=\dfrac{R A}{\rho}$
$=\dfrac{10 \times 3.14 \times(\dfrac{0.0005}{2})^{2}}{1.6 \times 10^{-8}}$
$=\dfrac{10 \times 3.14 \times 25}{4 \times 1.6}=122.72 m$
$\therefore$ length of the wire $=122.72 m$
If the diameter of the wire is doubled, new diameter $=2 \times 0.5=1 mm=0.001 m$ Let new resistance be $R^{\prime}$
$ \begin{aligned} & R^{\prime}=\rho_A^{l} \\ & =\dfrac{1.6 \times 10^{-8} \times 122.72}{\pi(\dfrac{1}{2} \times 10^{-3})^{2}} \\ & =\dfrac{1.6 \times 10^{-8} \times 122.72 \times 4}{3.14 \times 10^{-6}} \\ & =250.2 \times 10^{-2}=2.5 \Omega \end{aligned} $
Therefore, the length of the wire is $122.7 m$ and the new resistance is $2.5 \Omega$.
7. The values of current $I$ flowing in a given resistor for the corresponding values of potential difference $V$ across the resistor are given below -
| $I$ (amperes) | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 |
| $V$ (volts) | 1.6 | 3.4 | 6.7 | 10.2 | 13.2 |
Plot a graph between $V$ and $I$ and calculate the resistance of that resistor.
Show Answer
Answer
The plot between voltage and current is called $I V$ characteristic. The voltage is plotted on $x$-axis and current is plotted on $y$-axis. The values of the current for different values of the voltage are shown in the given table.
| $V$ (volts) | 1.6 | 3.4 | 6.7 | 10.2 | 13.2 |
|---|---|---|---|---|---|
| $I$ (amperes ) | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 |
The IV characteristic of the given resistor is plotted in the following figure.

The slope of the line gives the value of resistance $(R)$ as,
Slope $=1 / R=B C / A C=2 / 6.8$
$R=6.8 / 2=3.4 \Omega$
Therefore, the resistance of the resistor is $3.4 \Omega$.
8. When a $12 V$ battery is connected across an unknown resistor, there is a current of $2.5 mA$ in the circuit. Find the value of the resistance of the resistor.
Show Answer
Answer
Resistance $(R)$ of a resistor is given by Ohm’s law as, $V=I R$
$R=V / I$
Where,
Potential difference, $V=12 V$
Current in the circuit, $l=2.5 mA=2.5 \times 10^{-3} A$
$ R=\dfrac{12}{2.5 \times 10^{-3}}=4.8 \times 10^{3} \Omega=4.8 k \Omega $
Therefore, the resistance of the resistor is $4.8 k \Omega$
9. A battery of $9 V$ is connected in series with resistors of $0.2 \Omega, 0.3 \Omega, 0.4 \Omega, 0.5 \Omega$ and $12 \Omega$, respectively. How much current would flow through the $12 \Omega$ resistor?
Show Answer
Answer
There is no current division occurring in a series circuit. Current flow through the component is the same, given by Ohm’s law as
$V=I R$
$I=V / R$
Where,
$R$ is the equivalent resistance of resistances $0.2 \Omega, 0.3 \Omega, 0.4 \Omega, 0.5 \Omega$ and $12 \Omega$. These are connected in series. Hence, the sum of the resistances will give the value of $R$.
$R=0.2+0.3+0.4+0.5+12=13.4 \Omega$
Potential difference, $V=9 V$
$l=9 / 13.4=0.671 A$
Therefore, the current that would flow through the $12 \Omega$ resistor is $0.671 A$.
10. How many $176 \Omega$ resistors (in parallel) are required to carry $5 A$ on a $220 V$ line?
Show Answer
Answer
For $x$ number of resistors of resistance $176 \Omega$, the equivalent resistance of the resistors connected in parallel is given by Ohm’s law as $V=I R$
$R=V / I$
Where,
Supply voltage, $V=220 V$
Current, $I=5 A$
Equivalent resistance of the combination $=R$, given as
$ \begin{aligned} & \dfrac{1}{R}=x \times(\dfrac{1}{176}) \\ & R=\dfrac{176}{x} \end{aligned} $
From Ohm’s law,
$ \begin{aligned} & \dfrac{V}{I}=\dfrac{176}{x} \\ & x=\dfrac{176 \times I}{V}=\dfrac{176 \times 5}{220}=4 \end{aligned} $
Therefore, four resistors of $176 \Omega$ are required to draw the given amount of current.
11. Show how you would connect three resistors, each of resistance $6 \Omega$, so that the combination has a resistance of (i) $9 \Omega$, (ii) $4 \Omega$.
Show Answer
Answer
If we connect the resistors in series, then the equivalent resistance will be the sum of the resistors, i.e., $6 \Omega+6 \Omega+6 \Omega=18 \Omega$, which is not desired. If we connect the resistors in parallel, then the equivalent resistance will be $6 / 2=3 \Omega$ is also not desired. Hence, we should either connect the two resistors in series or parallel.
(a) Two resistor in parallel

Two $6 \Omega$ resistors are connected in parallel. Their equivalent resistance will be
$ \dfrac{1}{\dfrac{1}{6}+\dfrac{1}{6}}=\dfrac{6 \times 6}{6+6}=3 \Omega $
The third $6 \Omega$ resistor is in series with $3 \Omega$. Hence, the equivalent resistance of the circuit is $6 \Omega+$ $3 \Omega=9 \Omega$.
(b) Two resistor in series

Two $6 \Omega$ resistors are in series. Their equivalent resistance will be the sum $6+6=12 \Omega$. The third $6 \Omega$ resistor is in parallel with $12 \Omega$. Hence, equivalent resistance will be
$ \dfrac{1}{\dfrac{1}{12}+\dfrac{1}{6}}=\dfrac{12 \times 6}{12+6}=4 \Omega $
Therefore, the total resistance is $4 \Omega$.
12. Several electric bulbs designed to be used on a $220 V$ electric supply line, are rated $10 W$. How many lamps can be connected in parallel with each other across the two wires of $220 V$ line if the maximum allowable current is $5 A$ ?
Show Answer
Answer
Resistance $R_1$ of the bulb is given by the expression,
Supply voltage, $V=220 V$
Maximum allowable current, $I=5 A$
Rating of an electric bulb $P=10$ watts
Because $R=V^{2} / P$
$R 1=\dfrac{(220)^{2}}{10}=4840 \Omega$
According to Ohm’s law,
$V=I R$
Let $R$ is the total resistance of the circuit for $x$ number of electric bulbs
$R=V / I$
$=\dfrac{220}{5}=44 \Omega$
Resistance of each electric bulb, $R_1=4840 \Omega$
$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\ldots . .$. upto $x$ times.
$\dfrac{1}{R}=\dfrac{1}{R_1} \times x$
$x=\dfrac{R_1}{R}=\dfrac{4840}{44}=110$
$\therefore$ Number of electric bulbs connected in parallel are 110 .
13. A hot plate of an electric oven connected to a $220 V$ line has two resistance coils A and B, each of $24 \Omega$ resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Show Answer
Answer
Supply voltage, $V=220 V$
Resistance of one coil, $R=24 \Omega$
(i) Coils are used separately
According to Ohm’s law,
$V=I_1 R_1$
Where,
$I_1$ is the current flowing through the coil
$I_1=V / R_1=220 / 24=9.166 A$
Therefore, 9.16 A current will flow through the coil when used separately.
(ii) Coils are connected in series
Total resistance, $R_2=24 \Omega+24 \Omega=48 \Omega$
According to Ohm’s law, $V=I_2 R_2$
Where,
$I_2$ is the current flowing through the series circuit
$I_2=V / R_2=220 / 48=4.58 A$
Therefore, $4.58 A$ current will flow through the circuit when the coils are connected in series.
(iii) Coils are connected in parallel
Total resistance, $R_3$ is given as $=$
$ \dfrac{1}{\dfrac{1}{24}+\dfrac{1}{24}}=\dfrac{24}{2}=12 \Omega $
According to Ohm’s law,
$V=I_3 R_3$
Where,
$I_3$ is the current flowing through the circuit $I_3=V / R_3=220 / 12=18.33 A$
Therefore, 18.33 A current will flow through the circuit when coils are connected in parallel.
14. Compare the power used in the $2 \Omega$ resistor in each of the following circuits: (i) a $6 V$ battery in series with $1 \Omega$ and $2 \Omega$ resistors, and (ii) a $4 V$ battery in parallel with $12 \Omega$ and $2 \Omega$ resistors.
Show Answer
Answer
(i) Potential difference, $V=6 V$ $1 \Omega$ and $2 \Omega$ resistors are connected in series. Therefore, equivalent resistance of the circuit, $R=$ $1+2=3 \Omega$
According to Ohm’s law,
$V=I R$
Where,
$I$ is the current through the circuit
$1=6 / 3=2 A$
This current will flow through each component of the circuit because there is no division of current in series circuits. Hence, current flowing through the $2 \Omega$ resistor is 2 A. Power is given by the expression, $P=(I)^{2} R=(2)^{2} \times 2=8 W$
(ii) Potential difference, $V=4 V$
$12 \Omega$ and $2 \Omega$ resistors are connected in parallel. The voltage across each component of a parallel circuit remains the same. Hence, the voltage across $2 \Omega$ resistor will be $4 V$.
Power consumed by $2 \Omega$ resistor is given by
$P=V^{2} / R=4^{2} / 2=8 W$
Therefore, the power used by $2 \Omega$ resistor is $8 W$.
15. Two lamps, one rated $100 W$ at $220 V$, and the other $60 W$ at $220 V$, are connected in parallel to electric mains supply. What current is drawn from the line if the supply voltage is $220 V$ ?
Show Answer
Answer
Both the bulbs are connected in parallel. Therefore, potential difference across each of them will be $220 V$, because no division of voltage occurs in a parallel circuit.
Current drawn by the bulb of rating $100 W$ is given by,Power $=$ Voltage $x$ Current
Current $=$ Power/Voltage $=60 / 220 A$
Hence, current drawn from the line $=100 / 220+60 / 220=0.727$ A
16. Which uses more energy, a $250 W$ TV set in $1 hr$, or a $1200 W$ toaster in 10 minutes?
Show Answer
Answer
Energy consumed by an electrical appliance is given by the expression, $H=Pt$
Where,
Power of the appliance $=P$
Time $=t$
Energy consumed by a TV set of power $250 W$ in $1 h=250 \times 3600=9 \times 10^{5} J$
Energy consumed by a toaster of power $1200 W$ in 10 minutes $=1200 \times 600$
Energy consumed by a toaster of power $1200 W$ in 10 minutes $=1200 \times 600$
$=7.2 \times 10^{5} J$
Therefore, the energy consumed by a $250 W$ TV set in $1 h$ is more than the energy consumed by a toaster of power $1200 W$ in 10 minutes.
17. An electric heater of resistance $8 \Omega$ draws 15 A from the service mains 2 hours. Calculate the rate at which heat is developed in the heater.
Show Answer
Answer
Rate of heat produced by a device is given by the expression for power as, $P=I^{2} R$ Where, Resistance of the electric heater, $R=8 \Omega$
Current drawn, $I=15 A$
$P=(15)^{2} \times 8=1800 J / s$
Therefore, heat is produced by the heater at the rate of $1800 J / s$.
18. Explain the following.
(a) Why is the tungsten used almost exclusively for filament of electric lamps?
(b) Why are the conductors of electric heating devices, such as bread-toasters and electric irons, made of an alloy rather than a pure metal?
(c) Why is the series arrangement not used for domestic circuits?
(d) How does the resistance of a wire vary with its area of cross-section?
(e) Why are copper and aluminium wires usually employed for electricity transmission?
Show Answer
Answer
(a) The melting point and of Tungsten is an alloy which has very high melting point and very high resistivity so does not burn easily at a high temperature.
(b) The conductors of electric heating devices such as bread toasters and electric irons are made of alloy because resistivity of an alloy is more than that of metals which produces large amount of heat.
(c) In series circuits voltage is divided. Each component of a series circuit receives a small voltage so the amount of current decreases and the device becomes hot and does not work properly. Hence, series arrangement is not used in domestic circuits.
(d) Resistance (R) of a wire is inversely proportional to its area of cross-section (A), i.e. when area of cross section increases the resistance decreases or vice versa.
(e) Copper and aluminium are good conductors of electricity also they have low resistivity. So they are usually used for electricity transmission.
विघुत द्युत का आधुनिक समाज में एक महत्त्वपूर्ण स्थान है। यह घरों, विद्यालयों, अस्पतालों, उद्योगों तथा ऐसे ही अन्य संस्थानों के विविध उपयोगों के लिए एक नियंत्रित कर सकने योग्य और सुविधाजनक ऊर्जा का रूप है। वह क्या है, जिससे विद्युत बनती है? किसी विद्युत परिपथ में यह कैसे प्रवाहित होती है? वह कौन से कारक हैं, जो किसी विद्युत परिपथ की विद्युत धारा को नियंत्रित अथवा नियमित करते हैं। इस अध्याय में हम इस प्रकार के प्रश्नों के उत्तर देने का प्रयास करेंगे। हम विद्युत धारा के ऊष्मीय प्रभाव तथा इसके अनुप्रयोगों पर भी चर्चा करेंगे।
11.1 विद्युत धारा और परिपथ
हम वायु धारा तथा जल धारा से परिचित हैं। हम जानते हैं कि बहते हुए जल से नदियों में जल धारा बनती है। इसी प्रकार यदि विद्युत आवेश किसी चालक में से प्रवाहित होता है (उदाहरण के लिए किसी धातु के तार में से) तब हम यह कहते हैं कि चालक में विद्युत धारा है। हम जानते हैं कि किसी टॉर्च में सेल (अथवा बैटरी, जब उचित क्रम में रखे जाते हैं।) टॉर्च के बल्ब को दीप्ति करने के लिए आवेश का प्रवाह अथवा विद्युत धारा प्रदान करते हैं। हमने यह भी देखा है कि टॉर्च तभी प्रकाश देती है, जब उसके स्विच को ‘ऑन’ करते हैं। स्विच क्या कार्य करता है? स्विच सेल तथा बल्ब के बीच चालक संबंध जोड़ता है। किसी विद्युत धारा के सतत तथा बंद पथ को विद्युत परिपथ कहते हैं। अब यदि परिपथ कहीं से टूट जाए (अथवा टॉर्च के स्विच को ‘ऑफ’ कर दें।) तो विद्युत धारा का प्रवाह समाप्त हो जाता है तथा बल्ब दीप्ति नहीं करता।
हम विद्युत धारा को कैसे व्यक्त करें? विद्युत धारा को एकांक समय में किसी विशेष क्षेत्र से प्रवाहित आवेश के परिमाण द्वारा व्यक्त किया जाता है। दसरे शब्दों में, विद्युत आवेश के प्रवाह की दर को विद्युत धारा कहते हैं। उन परिपथों में जिनमें धातु के तार उपयोग होते हैं, आवेशों के प्रवाह की रचना इलेक्ट्रॉन करते हैं। तथापि, जिस समय विद्युत की परिघटना का सर्वप्रथम प्रेक्षण किया गया था, इलेक्ट्रॉनों के बारे में कोई जानकारी नहीं थी। अतः विद्युत धारा को धनावेशों का प्रवाह माना गया तथा धनावेश के प्रवाह की दिशा को ही विद्युत धारा की दिशा माना गया। परिपाटी के अनुसार किसी विद्युत परिपथ में इलेक्ट्रॉनों का जो ऋणावेश हैं, के प्रवाह की दिशा के विपरीत दिशा को विद्युत धारा की दिशा माना जाता है।

चित्र 11.1 एक सेल, एक विद्युत बल, एक ऐमीटर तथा एक प्लग कुंजी से मिलकर बने विद्युत परिपथ का व्यवस्था आरेख
यदि किसी चालक की किसी भी अनुप्रस्थ काट से समय $t$ में नेट आवेश $Q$ प्रवाहित होता है तब उस अनुप्रस्थ काट से प्रवाहित विद्युत धारा $I$ को इस प्रकार व्यक्त करते हैं-
$$ \begin{equation*} I=\frac{Q}{t} \tag{11.1} \end{equation*} $$
विद्युत आवेश का SI मात्रक कूलॉम $(\mathrm{C})$ है, जो लगभग $6 \times 10 _{18}$ इलेक्ट्रॉनों में समाए आवेश के तुल्य होता है। (हम जानते हैं कि एक इलेक्ट्रॉन पर $1.6 \times 10^{-19} \mathrm{C}$ आवेश होता है।) विद्युत धारा को एक मात्रक जिसे ऐम्पियर (A) कहते हैं, में व्यक्त किया जाता है। इस मात्रक का नाम आंद्रे-मेरी ऐम्पियर (1775-1836) नाम के फ्रांसीसी वैज्ञानिक के नाम पर रखा गया है। एक ऐम्पियर विद्युत धारा की रचना प्रति सेकंड एक कूलॉम आवेश के प्रवाह से होती है, अर्थात $1 \mathrm{~A}=1 \mathrm{C} / 1 \mathrm{~s}$ अल्प परिमाण की विद्युत धारा को मिलीऐम्पियर $\left(1 \mathrm{~mA}=10^{-3} \mathrm{~A}\right)$ अथवा माइक्रोऐम्पियर $\left(1 \mu \mathrm{A}=10^{-6} \mathrm{~A}\right)$ में व्यक्त करते हैं। परिपथों की विद्युत धारा मापने के लिए जिस यंत्र का उपयोग करते हैं, उसे ऐमीटर कहते हैं। इसे सदैव जिस परिपथ में विद्युत धारा मापनी होती है, उसके श्रेणीक्रम में संयोजित करते हैं। चित्र 11.1 में एक प्रतीकात्मक विद्युत परिपथ का व्यवस्था आरेख दिखाया गया है, जिसमें एक सेल, एक विद्युत बल्ब, एक ऐमीटर तथा प्लग कुंजी जुड़े हैं। ध्यान दीजिए परिपथ में विद्युत धारा, सेल के धन टर्मिनल से सेल के ऋण टर्मिनल तक बल्ब और ऐमीटर से होकर प्रवाहित होती है।
उदाहरण 11.1
किसी विद्युत बल्ब के तंतु में से $0.5 \mathrm{~A}$ विद्युत धारा 10 मिनट तक प्रवाहित होती है। विद्युत परिपथ से प्रवाहित विद्युत आवेश का परिमाण ज्ञात कीजिए।
हल
हमें दिया गया है, $I=0.5 \mathrm{~A} ; t=10 \mathrm{~min}=600 \mathrm{~s}$
समीकरण (11.1), से
$$ \begin{aligned} Q & =I t \\ & =0.5 A \times 600 s \\ & =300 C \end{aligned} $$
प्रश्न
1. विद्युत परिपथ का क्या अर्थ है?
Show Answer
#missing2. विद्युत धारा के मात्रक की परिभाषा लिखिए।
Show Answer
#missing3. एक कूलॉम आवेश की रचना करने वाले इलेक्ट्रॉनों की संख्या परिकलित कीजिए।
Show Answer
#missing11.2 विद्युत विभव और विभवांतर
वह क्या है, जो विद्युत आवेश को प्रवाहित कराता है? आइए, जल के प्रवाह से सदृश के आधार पर इसका विचार करते हैं। किसी कॉपर के तार से आवेश स्वयं प्रवाहित नहीं होते, ठीक वैसे ही जैसे किसी आदर्श क्षैतिज नली से जल प्रवाहित नहीं होता। यदि नली के एक सिरे को किसी उच्च तल पर रखे जल-टैंक से जोड़ दें, जिससे नली के दो सिरों के बीच कोई दाबांतर बन जाए, तो नली के मुक्त सिरे से जल बाहर की ओर प्रवाहित होता है। किसी चालक तार में आवेशों के प्रवाह के लिए वास्तव में, गुरुत्व बल की कोई भूमिका नहीं होती; इलेक्ट्रॉन केवल तभी गति करते हैं, जब चालक के अनुदिश वैद्युत दाब में कोई अंतर होता है, जिसे विभवांतर कहते हैं। विभव में यह अंतर एक या अधिक विद्युत सेलों से बनी बैटरी द्वारा उत्पन्न किया जा सकता है। किसी सेल के भीतर होने वाली रासायनिक अभिक्रिया सेल के टर्मिनलों के बीच विभवांतर उत्पन्न कर देती है, ऐसा उस समय भी होता है जब सेल से कोई विद्युत धारा नहीं ली जाती है। जब सेल को किसी चालक परिपथ अवयव से संयोजित करते हैं तो विभवांतर उस चालक के आवेशों में गति ला देता है और विद्युत धारा उत्पन्न हो जाती है। किसी विद्युत परिपथ में विद्युत धारा बनाए रखने के लिए सेल अपनी संचित रासायनिक ऊर्जा खर्च करता है।
किसी धारावाही विद्युत परिपथ के दो बिंदुओं के बीच विद्युत विभवांतर को हम उस कार्य द्वारा परिभाषित करते हैं, जो एकांक आवेश को एक बिंदु से दूसरे बिंदु तक लाने में किया जाता है।
दो बिंदुओं के बीच विभवांतर $(V)=\frac{\text { किया गया कार्य }(W)}{\text { आवेश }(Q)}$
$$ \begin{equation*} V=W / Q \tag{11.2} \end{equation*} $$
विद्युत विभवांतर का SI मात्रक वोल्ट $(\mathrm{V})$ है, जिसे इटली के भौतिकविज्ञानी अलेसान्द्रो वोल्टा के नाम पर रखा गया है। यदि किसी विद्युत धारावाही चालक के दो बिंदुओं के बीच एक कूलॉम आवेश को एक बिंदु से दूसरे बिंदु तक ले जाने में 1 जूल कार्य किया जाता है तो उन दो बिंदुओं के बीच विभवांतर 1 वोल्ट होता है। अतः
$$1 \text { वोल्ट }=\frac{1 \text { जूल }}{1 \text { कूलॉम }}$$
$$ \begin{equation*} 1 \mathrm{~V}=1 \mathrm{JC}^{-1} \tag{11.3} \end{equation*} $$
विभवांतर की माप एक यंत्र द्वारा की जाती है, जिसे वोल्टमीटर कहते हैं। वोल्टमीटर को सदैव उन बिंदुओं से पार्श्वक्रम संयोजित करते हैं, जिनके बीच विभवांतर मापना होता है।
उदाहरण 11.2
$12 \mathrm{~V}$ विभवांतर के दो बिंदुओं के बीच $2 \mathrm{C}$ आवेश को ले जाने में कितना कार्य किया जाता है?
हल
विभवांतर V $(=12$ वोल्ट) के दो बिंदुओं के बीच प्रवाहित आवेश का परिमाण $Q(=2$ कूलॉम) है। इस प्रकार आवेश को स्थानांतरित करने में किया गया कार्य (समीकरण 11.2 के अनुसार) है-
$$ \begin{matrix} W & = V Q \\ & = 12 V \times 2 C \\ & = 24 J . \end{matrix} $$
प्रश्न
1. उस युक्ति का नाम लिखिए, जो किसी चालक के सिरों पर विभवांतर बनाए रखने में सहायता करती है।
Show Answer
#missing2. यह कहने का क्या तात्पर्य है कि दो बिंदुओं के बीच विभवांतर $1 \mathrm{~V}$ है?
Show Answer
#missing3. $6 \mathrm{~V}$ बैटरी से गुज़रने वाले हर एक कूलॉम आवेश को कितनी ऊर्जा दी जाती है?
Show Answer
#missing11.3 विद्युत परिपथ आरेख
हम जानते हैं कि कोई विद्युत परिपथ जैसा चित्र 11.1 में दिखाया गया है, एक सेल (अथवा एक बैटरी), एक प्लग कुंजी, वैद्युत अवयव (अथवा अवयवों) तथा संयोजी तारों से मिलकर बनता है। विद्युत परिपथों का प्रायः ऐसा व्यवस्था आरेख खींचना सुविधाजनक होता है, जिसमें परिपथ के विभिन्न अवयवों को सुविधाजनक प्रतीकों द्वारा निरूपित किया जाता है। सारणी 11.1 में सामान्य उपयोग में आने वाले कुछ वैद्युत अवयवों को निरूपित करने वाले रूढ़ प्रतीक दिए गए हैं।
सारणी 11.1 : विद्युत परिपथों में सामान्यतः उपयोग होने वाले कुछ अवयवों के प्रतीक


11.4 ओम का नियम
क्या किसी चालक के सिरों के बीच विभवांतर और उससे प्रवाहित विद्युतधारा के बीच कोई संबंध है? आइए, एक क्रियाकलाप द्वारा इसकी छानबीन करते हैं।
क्रियाकलाप 11.1
- चित्र 11.3 में दिखाए अनुसार एक परिपथ तैयार कीजिए। इस परिपथ में लगभग $0.5 \mathrm{~m}$ लंबा निक्रोम का तार $\mathrm{XY}$, एक ऐमीटर, एक वोल्टमीटर तथा चार सेल जिनमें प्रत्येक $1.5 \mathrm{~V}$ का हो, जोड़िए। (निक्रोम निकैल, क्रोमियम, मेंगनीज तथा आयरन की एक मिश्रधातु है।)
- सबसे पहले परिपथ में विद्युत धारा के स्रोत के रूप में केवल एक सेल का उपयोग कीजिए। परिपथ में निक्रोम-तार $\mathrm{XY}$ से प्रवाहित होने वाली विद्युत धारा के लिए ऐमीटर का पाठ्यांक $I$, तार के सिरों के बीच विभवांतर के लिए वोल्टमीटर का पाठ्यांक $V$ लीजिए। इन्हें दी गई सारणी में लिखिए।

चित्र 11.2 ओम के नियम के अध्ययन के लिए विद्युत परिपथ
- इसके पश्चात परिपथ में दो सेल जोड़िए और निक्रोम तार में प्रवाहित होने वाली विद्युत धारा तथा इसके सिरों के बीच विभवांतर का मान ज्ञात करने के ऐमीटर तथा वोल्टमीटर के पाठ्यांक नोट कीजिए।
- उपरोक्त चरणों को, पहले तीन सेल और फिर चार सेलों को परिपथ में पृथक-पृथक लगाकर दोहराइए।
- विभवांतर $V$ तथा विद्युत धारा $I$ के प्रत्येक युगल के लिए अनुपात $V / I$ परिकलित कीजिए।
| क्रम संख्या | परिपथ में जुड़े सेलों की संख्या | निक्रोम-तार से प्रवाहित विद्युत धारा I (A) | निक्रोम-तार के सिरों पर विभवांतर $\mathrm{V}(\mathrm{V})$ | $\mathrm{V} / \mathrm{I}$ (वोल्ट/ऐम्पियर) |
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 2 | |||
| 3 | 3 | |||
| 4 | 4 |
- $V$ तथा $I$ के बीच ग्राफ खींचिए तथा इस ग्राफ की प्रकृति का प्रेक्षण कीजिए।

चित्र 11.3 निक्रोम तार के लिए $V-I$ ग्राफ। सरल रेखीय ग्राफ यह दर्शाता है कि जैसे-जैसे तार में प्रवाहित विद्युत धारा बढ़ती है विभवांतर रैखिकतः बढ़ता है। यही ओम का नियम है।
इस क्रियाकलाप में आप यह देखेंगे कि प्रत्येक प्रकरण में $V / I$ का लगभग एक ही मान प्राप्त होता है। इस प्रकार $V-I$ ग्राफ चित्र 11.3 में दिखाए अनुसार मूल बिंदु से गुज़रने वाली एक सरल रेखा होती है। इस प्रकार, $V / I$ एक नियत अनुपात है।
1827 में जर्मन भौतिकविज्ञानी जार्ज साईमन ओम ने किसी धातु के तार में प्रवाहित विद्युत धारा $I$ तथा उसके सिरों के बीच विभवांतर में परस्पर संबंध का पता लगाया। एक विद्युत परिपथ में धातु के तार के दो सिरों के बीच विभवान्तर उसमें प्रवाहित होने वाली विद्युत धारा के समानुपाती होता है, परंतु तार का ताप समान रहना चाहिए। इसे ओम का नियम कहते हैं। दसरे शब्दों में-
$ \begin{equation*} V \propto I \tag{11.6} \end{equation*} $
अथवा $\hspace{40 px } V/I = $ नियतांक
$ \hspace{70 px} = R $
अथवा
$ \begin{equation*} \hspace{50 px} V = IR \tag{11.5} \end{equation*} $
समीकरण (11.5) में किसी दिए गए धातु के लिए, दिए गए ताप पर, $R$ एक नियतांक है, जिसे तार का प्रतिरोध कहते हैं। किसी चालक का यह गुण है कि वह अपने में प्रवाहित होने वाले आवेश के प्रवाह का विरोध करता हैं। प्रतिरोध का SI मात्रक ओम है, इसे ग्रीक भाषा के शब्द $\Omega$ से निरूपित करते हैं। ओम के नियम के अनुसार-
$ \begin{equation*} R=V / I \tag{11.6} \end{equation*} $
यदि किसी चालक के दोनों सिरों के बीच विभवांतर $1 \mathrm{~V}$ है तथा उससे $1 \mathrm{~A}$ विद्युत धारा प्रवाहित होती है, तब उस चालक का प्रतिरोध $\mathrm{R}, 1 \Omega$ होता है।
$1 \text { ओम }=\frac{1 \text { वोल्ट }}{1 \text { ऐम्पियर }}$
समीकरण (11.5) से हमें यह संबंध भी प्राप्त होता है-
$ \begin{equation*} I=V / R \tag{11.7} \end{equation*} $
समीकरण (11.7) से स्पष्ट है कि किसी प्रतिरोधक से प्रवाहित होने वाली विद्युत धारा उसके प्रतिरोध के व्युत्क्रमानुपाती होती है। यदि प्रतिरोध दोगुना हो जाए तो विद्युत धारा आधी रह जाती है। व्यवहार में कई बार किसी विद्युत परिपथ में विद्युत धारा को घटाना अथवा बढ़ाना आवश्यक हो जाता है। स्रोत की वोल्टता में बिना कोई परिवर्तन किए परिपथ की विद्युत धारा को नियंत्रित करने के लिए उपयोग किए जाने वाले अवयव को परिवर्ती प्रतिरोध कहते हैं। किसी विद्युत परिपथ में परिपथ के प्रतिरोध को परिवर्तित करने के लिए प्रायः एक युक्ति का उपयोग करते हैं, जिसे धारा नियंत्रक कहते हैं। अब हम नीचे दिए गए क्रियाकलाप की सहायता से किसी चालक के विद्युत प्रतिरोध के विषय में अध्ययन करेंगे।
क्रियाकलाप 11.2
- एक निक्रोम तार, एक टॉर्च बल्ब, एक $10 \mathrm{~W}$ का बल्ब तथा एक ऐमीटर ( $0-5 \mathrm{~A}$ परिसर), एक प्लग कुंजी तथा कुछ संयोजी तार लीजिए।
- चार शुष्क सेलों (प्रत्येक $1.5 \mathrm{~V}$ का) को श्रेणीक्रम में ऐमीटर से संयोजित करके चित्र 11.4 में दिखाए अनुसार परिपथ में एक अंतराल $\mathrm{XY}$ छोड़कर एक परिपथ बनाइए।

चित्र 11.4
-
अंतराल $X Y$ में निक्रोम तार को जोड़कर परिपथ को पूरा कीजिए। कुंजी लगाइए। ऐमीटर का पाठ्यांक नोट कीजिए। प्लग से कुंजी बाहर निकालिए। (ध्यान दीजिए- परिपथ की धारा मापने के पश्चात सदैव ही प्लग से कुंजी बाहर निकालिए।)
-
निक्रोम तार के स्थान पर अंतराल $\mathrm{XY}$ में टार्च बल्ब को परिपथ में जोड़िए तथा ऐमीटर का पाठ्यांक लेकर बल्ब से प्रवाहित विद्युत धारा मापिए।
-
अंतराल $\mathrm{XY}$ में विभिन्न अवयवों को जोड़ने पर ऐमीटर के पाठ्यांक भिन्न-भिन्न हैं? उपरोक्त प्रेक्षण क्या संकेत देते हैं?
-
आप अंतराल $\mathrm{XY}$ में किसी भी पदार्थ का अवयव जोड़कर इस क्रियाकलाप को दोहरा सकते हैं। प्रत्येक स्थिति में ऐमीटर के पाठ्यांक का प्रेक्षण कीजिए। इन प्रेक्षणों का विश्लेषण कीजिए।
इस क्रियाकलाप में हम यह अवलोकन करते हैं कि विभिन्न अवयवों के लिए विद्युत धारा भिन्न है। यह भिन्न क्यों है? कुछ अवयव विद्युत धारा के प्रवाह के लिए सरल पथ प्रदान करते हैं, जबकि अन्य इस प्रवाह का विरोध करते हैं। हम यह जानते हैं कि इलेक्ट्रॉनों की किसी परिपथ में गति के कारण ही परिपथ में कोई विद्युत धारा बनती है। तथापि, चालक के भीतर इलेक्ट्रॉन गति करने के लिए पूर्णतः स्वतंत्र नहीं होते हैं, जिन परमाणुओं के बीच ये गति करते हैं, उन्हीं के आकर्षण द्वारा इनकी गति नियंत्रित हो जाती है। इस प्रकार किसी चालक से होकर इलेक्ट्रॉनों की गति उसके प्रतिरोध द्वारा मंद हो जाती है। एक ही साइज़ के चालकों में वह चालक जिसका प्रतिरोध कम होता है, अधिक अच्छा चालक होता है। वह चालक जो पर्याप्त प्रतिरोध लगाता है, प्रतिरोधक कहलाता है। सर्वसम साइज़ का वह अवयव जो उच्च प्रतिरोध लगाता है, हीन चालक कहलाता है। समान साइज़ का कोई विद्युतरोधी इससे भी अधिक प्रतिरोध लगाता है।
11.5 वह कारक जिन पर किसी चालक का प्रतिरोध निर्भर करता है
क्रियाकलाप 11.3
- एक सेल, एक ऐमीटर, $l$ लंबाई का एक निक्रोम तार [जैसे (1) द्वारा चिह्नित] तथा एक प्लग कुंजी चित्र 11.5 में दिखाए अनुसार जोड़कर एक विद्युत परिपथ पूरा कीजिए।

चित्र 11.5 उन कारकों जिन पर किसी चालक तार का प्रतिरोध निर्भर करता है, का अध्ययन करने के लिए विद्युत परिपथ
- अब प्लग में कुंजी लगाइए। ऐमीटर में विद्युत धारा नोट कीजिए।
- घस निक्रोम तार को अन्य निक्रोम तार से प्रतिस्थापित कीजिए, जिसकी मोटाई समान परंतु लंबाई दोगुनी हो, अर्थात 21 लंबाई का तार लीजिए जिसे चित्र 11.5 में (2) से चिह्नित किया गया है।
- ऐमीटर का पाठ्यांक नोट कीजिए।
- अब इस तार को समान लंबाई 1 के निक्रोम के मोटे तार [(3) से चिह्नित] से प्रतिस्थापित कीजिए। मोटे तार की अनुप्रस्थ काट का क्षेत्रफल अधिक होता है। परिपथ में प्रवाहित विद्युत धारा फिर नोट कीजिए।
- निक्रोम तार के स्थान पर ताँबे का तार [चित्र 11.5 में जिस पर चिह्न (4) बना है।] परिपथ में जोड़िए। मान लीजिए यह तार निक्रोम के तार जिस पर (1) चिह्नित है, के बराबर लंबा तथा समान अनुप्रस्थ काट के क्षेत्रफल का है। विद्युत धारा का मान नोट कीजिए।
- प्रत्येक प्रकरण में विद्युत धारा के मानों में अंतर को ध्यान से देखिए।
- क्या विद्युत धारा चालक की लंबाई पर निर्भर करती है?
- क्या विद्युत धारा उपयोग किए जाने वाले तार के अनुप्रस्थ काट के क्षेत्रफल पर निर्भर करती है?
यह पाया गया है कि जब तार की लंबाई दोगुनी कर देते हैं तो ऐमीटर का पाठ्यांक आधा हो जाता है। परिपथ में समान पदार्थ तथा समान लंबाई का मोटा तार जोड़ने पर ऐमीटर का पाठ्यांक बढ़ जाता है। ऐमीटर के पाठ्यांक में तब भी अंतर आता है जब परिपथ में भिन्न पदार्थ परंतु समान लंबाई तथा समान अनुप्रस्थ काट के क्षेत्रफल के तार को जोड़ते हैं। ओम के नियम [समीकरण (11.5) -(11.7)] को अनुप्रयोग करने पर हम यह पाते हैं कि किसी चालक का प्रतिरोध (i) चालक की लंबाई (ii) उसकी अनुप्रस्थ काट के क्षेत्रफल तथा (iii) उसके पदार्थ की प्रकृति पर निर्भर करता है। परिशुद्ध माप यह दर्शाते हैं कि किसी धातु के एकसमान चालक का प्रतिरोध उसकी लंबाई (1) के अनुक्रमानुपाती तथा उसकी अनुप्रस्थ काट के क्षेत्रफल (A) के व्युत्क्रमानुपाती होता है। अर्थात्
$$ \begin{equation*} R \propto l \tag{11.8} \end{equation*} $$
तथा
$$ \begin{equation*} \mathrm{R} \propto 1 / \mathrm{A} \tag{11.9} \end{equation*} $$
समीकरणों (11.8) तथा (11.9) को संयोजित करने पर हमें प्राप्त होता है
$$ \begin{aligned} R & \propto \frac{l}{A} \\ \text{ अथवा, } \quad R & =\rho \frac{l}{A} \qquad \qquad (11.10) \end{aligned} $$
यहाँ $\rho$ (रो) आनुपातिकता स्थिरांक है, जिसे चालक के पदार्थ की वैद्युत प्रतिरोधकता कहते हैं। प्रतिरोधकता का SI मात्रक $\Omega \mathrm{m}$ है। यह किसी पदार्थ का अभिलाक्षणिक गुणधर्म है। धातुओं तथा मिश्रातुओं की प्रतिरोधकता अत्यंत कम होती है, जिसका परिसर $10^{-8} \Omega \mathrm{m}$ से $10^{-6} \Omega \mathrm{m}$ है। ये विद्युत की अच्छी चालक हैं। रबड़ तथा काँच जैसे विद्युतरोधी पदार्थों की प्रतिरोधकता $10^{12}$ से $10^{17} \Omega \mathrm{m}$ कोटि की होती है। किसी पदार्थ का प्रतिरोध तथा प्रतिरोधकता दोनों ही ताप में परिवर्तन के साथ परिवर्तित हो जाते हैं।
सारणी 11.2 में हम यह देखते हैं कि व्यापक रूप में मिश्रातुओं की प्रतिरोधकता उनकी अवयवी धातुओं की अपेक्षा अधिक होती है। मिश्रातुओं का उच्च ताप पर शीघ्र ही उपचयन (दहन) नहीं होता। यही कारण है कि मिश्रातुओं का उपयोग विद्युत-इस्तरी, टोस्टर आदि सामान्य वैद्युत तापन युक्तियों के निर्माण में किया जाता है। विद्युत बल्बों के तंतुओं के निर्माण में तो एकमात्र टंगस्टन का ही उपयोग किया जाता है, जबकि कॉपर तथा ऐलुमिनियम का उपयोग विद्युत संचरण के लिए उपयोग होने वाले तारों के निर्माण में किया जाता है।
सारणी $11.220^{\circ} \mathrm{C}$ पर कुछ पदार्थों की वैद्युत प्रतिरोधकता*
| पदार्थ | प्रतिरोध $(\Omega \mathbf{~ m})$ | |
|---|---|---|
| चालक | सिल्वर | $1.60 \times 10^{-8}$ |
| कॉपर | $1.62 \times 10^{-8}$ | |
| ऐलुमिनियम | $2.63 \times 10^{-8}$ | |
| टंगस्टन | $5.20 \times 10^{-8}$ | |
| निकैल | $6.84 \times 10^{-8}$ | |
| आयरन | $10.0 \times 10^{-8}$ | |
| क्रोमियम | $12.9 \times 10^{-8}$ | |
| मर्करी | $94.0 \times 10^{-8}$ | |
| मैगनीज़ | $1.84 \times 10^{-6}$ | |
| मिश्रातुएँ | कांस्टेंटन | $49 \times 10^{-6}$ |
| (Cu तथा $\mathrm{Ni}$ की मिश्रातु) | ||
| मैंगनीज़ | $44 \times 10^{-6}$ | |
| $(\mathrm{Cu}, \mathrm{Mn}$ तथा $\mathrm{Ni}$ की मिश्रातु) | ||
| निक्रोम | $100 \times 10^{-6}$ | |
| ( $\mathrm{Ni}, \mathrm{Cr}, \mathrm{Mn}$ तथा $\mathrm{Fe}$ की मिश्रातु) | ||
| विद्युतरोधी | काँच | $10^{10}-10^{14}$ |
| कठोर | $10^{13}-10^{16}$ | |
| ऐबोनाइट | $10^{15}-10^{17}$ | |
| डायमंड | $10^{12}-10^{13}$ | |
| कागज़ (शुष्क) | $10^{12}$ |
- आपको इन मानों को याद करने की कोई आवश्यकता नहीं है। इन मानों का उपयोग आप आंकिक प्रश्नों को हल करने के लिए कर सकते हैं।
उदाहरण 11.3
(a) यदि किसी विद्युत बल्ब के तंतु का प्रतिरोध $1200 \Omega$ है तो यह बल्ब $220 \mathrm{~V}$ स्रोत से कितनी विद्युत धारा लेगा? (b) यदि किसी विद्युत हीटर की कुंडली का प्रतिरोध 100 $\Omega$ है तो यह विद्युत हीटर $220 \mathrm{~V}$ स्रोत से कितनी धारा लेगा?
हल
(a) हमें दिया गया है $V=220 \mathrm{~V} ; R=1200 \Omega$
समीकरण (11.6) से विद्युत धारा $I=220 \mathrm{~V} / 1200 \Omega = 0.18 \mathrm{~A}$
(b) हमें दिया गया है $V=220 \mathrm{~V} ; R=100 \Omega$
समीकरण (11.6) से विद्युत धारा $I=220 \mathrm{~V} / 100 \Omega = 2.2 \mathrm{~A}$
$220 \mathrm{~V}$ के समान विद्युत स्रोत से विद्युत बल्ब तथा विद्युत हीटर द्वारा ली जाने वाली विद्युत धाराओं के अंतर पर ध्यान दीजिए!
उदाहरण 11.4
जब कोई विद्युत हीटर विद्युत स्रोत से $4 \mathrm{~A}$ विद्युत धारा लेता है तब उसके टर्मिनलों के बीच विभवांतर $60 \mathrm{~V}$ है। उस समय विद्युत हीटर कितनी विद्युत धारा लेगा जब विभवांतर को 120 $\mathrm{V}$ तक बढ़ा दिया जाएगा?
हल
हमें दिया गया है, विभवांतर $V=60 \mathrm{~V}$, विद्युत धारा $I=4 \mathrm{~A}$
ओम के नियम के अनुसार, $R=\frac{V}{I}=\frac{60 \mathrm{~V}}{4 \mathrm{~A}}=15 \Omega$
जब विभवांतर बढ़ाकर $120 \mathrm{~V}$ किया जाता है, तब
विद्युतधारा $I=\frac{V}{R}=\frac{120 \mathrm{~V}}{15 \Omega}=8 \mathrm{~A}$
अर्थात, तब विद्युत हीटर से प्रवाहित विद्युत धारा का मान $8 \mathrm{~A}$ हो जाता है।
उदाहरण 11.5
किसी धातु के $1 \mathrm{~m}$ लंबे तार का $20^{\circ} \mathrm{C}$ पर वैद्युत प्रतिरोध $26 \Omega$ है। यदि तार का व्यास $0.3 \mathrm{~mm}$ है, तो इस ताप पर धातु की वैद्युत प्रतिरोधकता क्या है? सारणी 11.2 का उपयोग करके तार के पदार्थ की भविष्यवाणी कीजिए।
हल
हमें दिया गया है तार का प्रतिरोध $R=26 \Omega$, व्यास $d=0.3 \mathrm{~mm}=3 \times 10^{-4} \mathrm{~m}$, तथा तार की लंबाई $l=1 \mathrm{~m}$
अतः, समीकरण (11.10) से, दिए गए धातु के तार की वैद्युत प्रतिरोधकता
$\rho=(R A / l)=\left(R \pi d^{2} / 4 l\right)$
मानों को प्रतिस्थापित करने पर हमें प्राप्त होता है
$\rho=1.84 \times 10^{-6} \Omega \mathrm{m}$,
इस प्रकार दिए गए तार की धातु की $20^{\circ} \mathrm{C}$ पर वैद्युत प्रतिरोधकता $1.84 \times 10^{-6} \Omega \mathrm{m}$ है। सारणी 11.2 में हम देखते हैं कि मैंगनीज़ की वैद्युत प्रतिरोधकता का मान यही है।
उदाहरण 11.6
दिए गए पदार्थ की किसी 1 लंबाई तथा $A$ मोटाई के तार का प्रतिरोध $4 \Omega$ है। इसी पदार्थ के किसी अन्य तार का प्रतिरोध क्या होगा जिसकी लंबाई $\frac{l}{2}$ तथा मोटाई $2 \mathrm{~A}$ है?
हल
प्रथम तार के लिए
$ R_1=\rho \frac{l}{A}=4 \Omega $
द्वितीय तार के लिए
$R_2=\rho \frac{l / 2}{2 A}=\frac{1}{4} \rho \frac{l}{A}$
$R_2=\frac{1}{4} \quad R_1$
$R_2=1 \Omega$
अतः तार का नया प्रतिरोध $1 \Omega$ है।
प्रश्न
1. किसी चालक का प्रतिरोध किन कारकों पर निर्भर करता है?
Show Answer
#missing2. समान पदार्थ के दो तारों में यदि एक पतला तथा दूसरा मोटा हो तो इनमें से किसमें विद्युत धारा आसानी से प्रवाहित होगी, जबकि उन्हें समान विद्युत स्रोत से संयोजित किया जाता है? क्यों?
Show Answer
#missing3. मान लीजिए किसी वैद्युत अवयव के दो सिरों के बीच विभवांतर को उसके पर्व के विभवांतर की तुलना में घटाकर आधा कर देने पर भी उसका प्रतिरोध नियत रहता है। तब उस अवयव से प्रवाहित होने वाली विद्युत धारा में क्या परिवर्तन होगा?
Show Answer
#missing4. विद्युत टोस्टरों तथा विद्युत इस्तरियों के तापन अवयव शुद्ध धातु के न बनाकर किसी मिश्रातु के क्यों बनाए जाते हैं?
Show Answer
#missing5. निम्नलिखित प्रश्नों के उत्तर तालिका 11.2 में दिए गए आँकड़ों के आधार पर दीजिए-
(a) आयरन $(\mathrm{Fe})$ तथा मर्करी $(\mathrm{Hg})$ में कौन अच्छा विद्युत चालक है?
(b) कौन-सा पदार्थ सर्वश्रेष्ठ चालक है?
Show Answer
#missing11.6 प्रतिरोधकों के निकाय का प्रतिरोध
पिछले अनुभाग में हमने कुछ सरल विद्युत परिपथों के बारे में सीखा था। हमने यह देखा कि किसी चालक से प्रवाहित होने वाली विद्युत धारा का मान किस प्रकार उसके प्रतिरोध तथा उसके सिरों के बीच विभवांतर पर निर्भर करता है। विविध प्रकार के विद्युत उपकरणों तथा युक्तियों में हम प्रायः प्रतिरोधकों के विविध संयोजन देखते हैं। इसलिए, अब हमें यह विचार करना है कि प्रतिरोधकों के संयोजनों पर ओम के नियम को किस प्रकार अनुप्रयुक्त किया जा सकता है?
प्रतिरोधकों को परस्पर संयोजित करने की दो विधियाँ हैं। चित्र 11.6 में एक विद्युत परिपथ दिखाया गया है, जिसमें $R _{1}, R _{2}$ तथा $R _{3}$ प्रतिरोध के तीन प्रतिरोधकों को एक सिरे से दूसरा सिरा मिलाकर जोड़ा गया है। प्रतिरोधकों के इस संयोजन को श्रेणीक्रम संयोजन कहा जाता है।

चित्र 11.6 श्रेणीक्रम में संयोजित प्रतिरोधक
चित्र 11.7 में प्रतिरोधकों का एक ऐसा संयोजन दिखाया गया है जिसमें तीन प्रतिरोधक एक साथ बिंदुओं $X$ तथा $Y$ के बीच संयोजित हैं। प्रतिरोधकों के इस प्रकार के संयोजन को पार्श्वक्रम संयोजन कहा जाता है।

चित्र 11.7 पार्श्वक्रम में संयोजित प्रतिरोधक
11.6.1 श्रेणीक्रम में संयोजित प्रतिरोधक
जब कई प्रतिरोधकों को श्रेणीक्रम में संयोजित करते हैं तो परिपथ में प्रवाहित विद्युत धारा का क्या होता है? उनका तुल्य प्रतिरोध क्या होता है? आइए, इसे निम्नलिखित क्रियाकलापों की सहायता से समझने का प्रयास करते हैं।
क्रियाकलाप 11.4
- विभिन्न मानों के तीन प्रतिरोधकों को श्रेणीक्रम में जोड़िए। चित्र 11.6 में दिखाए अनुसार इन्हें एक बैटरी, एक ऐमीटर तथा एक प्लग कुंजी से संयोजित कीजिए। आप $1 \Omega, 2 \Omega, 3 \Omega$ आदि मानों के प्रतिरोधकों का उपयोग कर सकते हैं तथा इस क्रियाकलाप के लिए $6 \mathrm{~V}$ की बैटरी उपयोग में ला सकते हैं।
- कुंजी को प्लग में लगाइए तथा ऐमीटर का पाठ्यांक नोट कीजिए।
- ऐमीटर की स्थिति को दो प्रतिरोधकों के बीच कहीं भी परिवर्तित कर सकते हैं। हर बार ऐमीटर का पाठ्यांक नोट कीजिए।
- क्या आप ऐमीटर के द्वारा विद्युत धारा के मान में कोई अंतर पाते हैं?
आप यह देखेंगे कि ऐमीटर में विद्युत धारा का मान वही रहता है, यह परिपथ में ऐमीटर की स्थिति पर निर्भर नहीं करता है। इसका तात्पर्य यह है कि प्रतिरोधकों के श्रेणीक्रम संयोजन में परिपथ के हर भाग में विद्युत धारा समान होती है अर्थात प्रत्येक प्रतिरोध से समान विद्युत धारा प्रवाहित होती है।
क्रियाकलाप 11.5
- क्रियाकलाप 11.4 में चित्र 11.6 में दिखाए अनुसार तीन प्रतिरोधकों के श्रेणीक्रम संयोजन के सिरों $X$ तथा $Y$ के बीच एक वोल्टमीटर लगाइए।
- परिपथ में प्लग में कुंजी लगाइए तथा वोल्टमीटर का पाठ्यांक नोट कीजिए। इससे हमें श्रेणीक्रम संयोजन के सिरों के बीच विभवांतर ज्ञात होता है। मान लीजिए यह $V$ है। अब बैटरी के दोनों टर्मिनलों के बीच विभवांतर नोट कीजिए। इन दोनों मानों की तुलना कीजिए।
- प्लग से कुंजी निकालिए तथा वोल्टमीटर को भी परिपथ से हटा दीजिए। अब वोल्टमीटर को चित्र 11.8 में दिखाए अनुसार पहले प्रतिरोधक के सिरों $\mathrm{X}$ तथा $\mathrm{P}$ के बीच जोड़िए।
- प्लग में कुंजी लगाइए तथा पहले प्रतिरोधक के सिरों के बीच विभवांतर मापिए। मान लीजिए यह $V _{l}$ है।
- इसी प्रकार अन्य दो प्रतिरोधकों के सिरों के बीच पृथक-पृथक विभवांतर मापिए। मान लीजिए ये मान क्रमशः $V _{2}$ तथा $V _{3}$ हैं।
- $V, V _{l}, V _{2}$ तथा $\mathrm{V} _{3}$ के बीच संबंध व्युत्पन्न कीजिए।

चित्र 11.8
आप यह देखेंगे कि विभवांतर $V$ अन्य तीन विभवांतरों, $V _{1}, V _{2}$ तथा $V _{3}$ के योग के बराबर है अर्थात प्रतिरोधक के श्रेणीक्रम संयोजन के सिरों के बीच कुल विभवांतर व्यष्टिगत प्रतिरोधकों के विभवांतरों के योग के बराबर है अर्थात-
$$ \begin{equation*} V=V _{1}+V _{2}+V _{3} \tag{11.11} \end{equation*} $$
मान लीजिए, चित्र 11.8 विद्युत में दर्शाए गए परिपथ में प्रवाहित विद्युत धारा $I$ है। तब प्रत्येक प्रतिरोधक से प्रवाहित विद्युत धारा भी $I$ है। श्रेणीक्रम में जुड़े इन तीनों प्रतिरोधकों को एक ऐसे तुल्य एकल प्रतिरोधक जिसका प्रतिरोध $R$ है, के द्वारा प्रतिस्थापित करना संभव है, जिसे परिपथ में जोड़ने पर इसके सिरों पर प्रतिरोध $V$ तथा परिपथ में प्रवाहित धारा $I$ वही रहती है। समस्त परिपथ पर ओम का नियम अनुप्रयुक्त करने पर हमें प्राप्त होता है-
$$ \begin{equation*} V=I R \tag{11.12} \end{equation*} $$
तीनों प्रतिरोधकों पर पृथक-पृथक ओम का नियम अनुप्रयुक्त करने पर हमें प्राप्त होता है-
$$ \begin{align*} & V _{1}=I R _{1} \tag{11.13a} \\ & V _{2}=I R _{2} \tag{11.13b} \\ \text {तथा} & V _{3}=I R _{3} \tag{11.13c} \end{align*} $$
समीकरण (11.11) से
$$ I R=I R _{1}+I R _{2}+I R _{3} $$
अथवा
$ \begin{equation*} R s=R _{1}+R _{2}+R _{3} \tag{11.14} \end{equation*} $
इस प्रकार हम यह निष्कर्ष निकाल सकते हैं कि जब बहुत से प्रतिरोधक श्रेणीक्रम में संयोजित होते हैं तो संयोजन का कुल प्रतिरोध $R _{1}, R _{2}, R _{3}$ के योग के बराबर होता है और इस प्रकार संयोजन का प्रतिरोध किसी भी व्यष्टिगत प्रतिरोधक के प्रतिरोध से अधिक होता है।
उदाहरण 11.7
एक विद्युत लैम्प जिसका प्रतिरोध 20 है, तथा एक $4 \Omega$ प्रतिरोध का चालक $6 \mathrm{~V}$ की बैटरी से चित्र 11.9 में दिखाए अनुसार संयोजित हैं। (a) परिपथ का कुल प्रतिरोध, (b) परिपथ में प्रवाहित विद्युत धारा तथा (c) विद्युत लैम्प तथा चालक के सिरों के बीच विभवांतर परिकलित कीजिए।

चित्र $11.96 \mathrm{~V}$ की बैटरी से श्रेणीक्रम में संयोजित एक विद्युत लैम्प तथा $4 \Omega$ का एक प्रतिरोधक
हल
विद्युत लैम्प का प्रतिरोध $R _{1}=20 \Omega$
श्रेणीक्रम में संयोजित चालक का प्रतिरोध $R _{2}=4 \Omega$
तब, परिपथ में कुल प्रतिरोध
$R=R _{1}+R _{2}$
$R _{s}=20 \Omega+4 \Omega=24 \Omega$
बैटरी के दो टर्मिनलों के बीच कुल विभवांतर $\mathrm{V}=6 \mathrm{~V}$
अब, ओम के नियम के अनुसार परिपथ में प्रवाहित कुल विद्युत धारा
$$ \begin{aligned} I & =V / R _{s} \\ & =6 V / 24 \Omega \\ & =0.25 \mathrm{~A} \end{aligned} $$
विद्युत लैम्प तथा चालक पर ओम का नियम पृथक-पृथक अनुप्रयुक्त करने पर हमें विद्युत लैम्प के सिरों के बीच विभवांतर प्राप्त होता है-
$V _{1}=20 \Omega \times 0.25 \mathrm{~A}$
$=5 \mathrm{~V}$;
तथा,
चालक के सिरों के बीच विभवांतर प्राप्त होता है- $V_2=4 \Omega \times 0.25 A = 1 V$.
अब मान लीजिए हम विद्युत लैम्प तथा चालक के श्रेणीक्रम संयोजन को किसी एकल तथा तुल्य प्रतिरोधक से प्रतिस्थापित करना चाहते हैं। इस तुल्य प्रतिरोधक का प्रतिरोध इतना होना चाहिए कि इसे $6 \mathrm{~V}$ बैटरी के दो टर्मिनलों से संयोजित करने पर परिपथ में $0.25 \mathrm{~A}$ विद्युत धारा प्रवाहित हो। तब इस तुल्य प्रतिरोधक का प्रतिरोध $R$ होगा-
$$ \begin{aligned} R & =V / I \\ & =6 \mathrm{~V} / 0.25 \mathrm{~A} \\ & =24 \Omega \end{aligned} $$
यह श्रेणीक्रम परिपथ का कुल प्रतिरोध है; यह दोनों प्रतिरोधों के योग के बराबर है।
प्रश्न
1. किसी विद्युत परिपथ का व्यवस्था आरेख खींचिए, जिसमें $2 \mathrm{~V}$ के तीन सेलों की बैटरी, एक $5 \Omega$ प्रतिरोधक, एक $8 \Omega$ प्रतिरोधक, एक $12 \Omega$ प्रतिरोधक तथा एक प्लग कुंजी सभी श्रेणीक्रम में संयोजित हों।
Show Answer
#missing2. प्रश्न 1 का परिपथ दुबारा खींचिए तथा इसमें प्रतिरोधकों से प्रवाहित विद्युत धारा को मापने के लिए ऐमीटर तथा $12 \Omega$ के प्रतिरोधक के सिरों के बीच विभवांतर मापने के लिए वोल्टमीटर लगाइए। ऐमीटर तथा वोल्टमीटर के क्या पाठ्यांक होंगे?
Show Answer
#missing11.6.2 पार्श्वक्रम में संयोजित प्रतिरोधक
आइए अब चित्र 11.7 में दिखाए अनुसार, जोड़े गये सेलों के एक संयोजन (अथवा बैटरी) से पार्श्वक्रम में संयोजित तीन प्रतिरोधकों की व्यवस्था पर विचार करते हैं।

चित्र 11.10
क्रियाकलाप 11.6
- तीन प्रतिरोधकों जिनके प्रतिरोध क्रमशः $R _{1}, R _{2}$ तथा $\mathrm{R} _{3}$ हैं, का पार्श्व संयोजन $\mathrm{XY}$ बनाइए। चित्र 11.10 में दिखाए अनुसार इस संयोजन को एक बैटरी, एक प्लग कुंजी तथा एक ऐमीटर से संयोजित कीजिए। प्रतिरोधकों के संयोजन के पार्श्वक्रम में एक वोल्टमीटर भी संयोजित कीजिए।
- प्लग में कुंजी लगाइए तथा ऐमीटर का पाठ्यांक नोट कीजिए। मान लीजिए विद्युत धारा का मान $I$ है। वोल्टमीटर का पाठ्यांक भी नोट कीजिए। इससे पार्श्व संयोजन के सिरों के बीच विभवांतर $V$ प्राप्त होता है। प्रत्येक प्रतिरोधक के सिरों के बीच विभवांतर भी $V$ है। इसकी जाँच प्रत्येक प्रतिरोधक के सिरों पर पृथक-पृथक वोल्टमीटर संयोजित करके की जा सकती है। (चित्र 11.11 देखिए)
- कुंजी से प्लग बाहर निकालिए। परिपथ से ऐमीटर तथा वोल्टमीटर निकाल लीजिए। चित्र 11.11 में दिखाए अनुसार ऐमीटर को प्रतिरोध $R _{I}$ से श्रेणीक्रम में संयोजित कीजिए। ऐमीटर का पाठ्यांक $I$, नोट कीजिए।

चित्र 11.11
- इसी प्रकार, $R _{l}$ एवं $R _{2}$ में प्रवाहित होने वाली धारा भी मापिए। माना इनका मान क्रमशः $I _{l}$ एवं $I _{2}$ है। $I, I _{1}, I _{2}$ एवं $I _{3}$ में क्या संबंध है?
यह पाया जाता है कि कुल विद्युत धारा $I$, संयोजन की प्रत्येक शाखा में प्रवाहित होने वाली पृथक धाराओं के योग के बराबर है।
$I=I _{1}+I _{2}+I _{3}$
मान लीजिए प्रतिरोधकों के पार्श्व संयोजन का तुल्य प्रतिरोध $R _{p}$ है। प्रतिरोधकों के पार्श्व संयोजन पर ओम का नियम लाग करने पर हमें प्राप्त होता है
$I=V / R _{p}$
प्रत्येक प्रतिरोधक पर ओम का नियम लागू करने पर हमें प्राप्त होता है
$I _{1}=V / R _{1} ; \quad I _{2}=V / R _{2} ;$ और $I _{3}=V / R _{3}$
समीकरणों (11.15) तथा (11.17) से हमें प्राप्त होता है
$$ V / R _{p}=V / R _{1}+V / R _{2}+V / R _{3} $$
अथवा
$$ \begin{equation*} 1 / R _{p}=1 / R _{1}+1 / R _{2}+1 / R _{3} \tag{11.18} \end{equation*} $$
इस प्रकार हम यह निष्कर्ष निकाल सकते हैं कि पार्श्वक्रम से संयोजित प्रतिरोधों के समूह के तुल्य प्रतिरोध का व्युत्क्रम पृथक प्रतिरोधों के व्युत्क्रमों के योग के बराबर होता है।
उदाहरण 11.8
चित्र 11.10 के परिपथ आरेख में मान लीजिए प्रतिरोधकों $R _{1}, R _{2}$ तथा $R _{3}$ के मान क्रमशः $5 \Omega, 10 \Omega, 30 \Omega$ हैं तथा इन्हें $12 \mathrm{~V}$ की बैटरी से संयोजित किया गया है। (a) प्रत्येक प्रतिरोधक से प्रवाहित विद्युत धारा (b) परिपथ में प्रवाहित कुल विद्युत धारा तथा (c) परिपथ का कुल प्रतिरोध परिकलित कीजिए।
हल
$R _{1}=5 \Omega, R _{2}=10 \Omega$, तथा $R _{3}=30 \Omega$
बैटरी के सिरों पर विभवांतर, $\mathrm{V}=12 \mathrm{~V}$
प्रत्येक व्यष्टिगत प्रतिरोधक के सिरों पर भी विभवांतर इतना ही है, अतः प्रतिरोधकों से प्रवाहित विद्युत धारा का परिकलन करने के लिए हम ओम के नियम का उपयोग करते हैं।
$R _{l}$ से प्रवाहित विद्युत धारा $I _{l} \quad=V / R _{l}$
$ I _{1}=12 \mathrm{~V} / 5 \Omega=2.4 \mathrm{~A} $
$R _{2}$ से प्रवाहित विद्युत धारा $I _{2}=V / R _{2}$
$ I _{2}=12 \mathrm{~V} / 10 \Omega=1.2 \mathrm{~A} $
$R _{3}$ से प्रवाहित विद्युत धारा $I _{3}=V / R _{3}$
$ I _{3}=12 \mathrm{~V} / 30 \Omega=0.4 \mathrm{~A} $
परिपथ से प्रवाहित कुल धारा
$ \begin{aligned} I & =I _{1}+I _{2}+I _{3} \\ & =(2.4+1.2+0.4) \mathrm{A} \\ & =4 \mathrm{~A} \end{aligned} $
समीकरण (12.18) से कुल प्रतिरोध $R _{p}$, का मान इस प्रकार प्राप्त किया जा सकता है
$\frac{1}{R _{p}}=\frac{1}{5}+\frac{1}{10}+\frac{1}{30}=\frac{1}{3}$
इस प्रकार $R _{p}=3 \Omega$
उदाहरण 11.9
चित्र 11.12, में $R _{1}=10 \Omega, R _{2}=40 \Omega, R _{3}=30 \Omega, R _{4}=20 \Omega$, $R _{5}=60 \Omega$, है तथा प्रतिरोधकों के इस विन्यास को $12 \mathrm{~V}$ से संयोजित किया जाता है। (a) परिपथ में कुल प्रतिरोध तथा (b) परिपथ में प्रवाहित कुल विद्युत धारा परिकलित कीजिए।
हल
मान लीजिए इन पार्श्वक्रम में संयोजित दो प्रतिरोधकों $R _{1}$ तथा $R _{2}$ को किसी तुल्य प्रतिरोधक जिसका प्रतिरोध $R^{\prime}$. है, द्वारा प्रतिस्थापित करते हैं। इस प्रकार हम पार्श्वक्रम में संयोजित तीन प्रतिरोधकों $R _{3}, R _{4}$ तथा $R _{5}$ को किसी अन्य तुल्य प्रतिरोधक जिसका प्रतिरोध $R^{\prime \prime}$ द्वारा प्रतिस्थापित करते हैं। तब समीकरण (11.19) का उपयोग करने पर हमें प्राप्त होता है $1 / R^{\prime}=1 / 10+1 / 40=5 / 40$; अर्थात $R^{\prime}=8 \Omega$
इसी प्रकार $\quad 1 / R^{\prime \prime}=1 / 30+1 / 20+1 / 60=6 / 60$;
अर्थात $R^{\prime \prime}=10 \Omega$
इस प्रकार, कुल प्रतिरोध, $R=R^{\prime}+R^{\prime \prime}=18 \Omega$
विद्युत धारा का मान परिकलित करने के लिए ओम का नियम उपयोग करने पर हमें प्राप्त होता है- $I=V / R=12 \mathrm{~V} / 18 \Omega=0.67 \mathrm{~A}$
हमने देखा है कि किसी श्रेणीबद्ध विद्युत परिपथ में शुरू से अंत तक विद्युत धारा नियत रहती है। इस प्रकार स्पष्ट रूप से यह व्यावहारिक नहीं है कि हम किसी विद्युत परिपथ में विद्युत बल्ब तथा विद्युत हीटर को श्रेणीक्रम में संयोजित करें। इसका कारण यह है कि इन्हें उचित प्रकार से कार्य करने के लिए अत्यधिक भिन्न मानों की विद्युत धाराओं की आवश्यकता होती है। (उदाहरण 11.3 देखिए।) श्रेणीबद्ध परिपथ से एक प्रमुख हानि यह होती है कि जब परिपथ का एक अवयव कार्य करना बंद कर देता है तो परिपथ टूट जाता है और परिपथ का अन्य कोई अवयव कार्य नहीं कर पाता। यदि आपने त्यौहारों, विवाहोत्सवों आदि पर भवनों की सजावट में बल्बों की सजावटी लड़ियों का उपयोग होते देखा है तो आपने बिजली-मिस्त्ररी को परिपथ में खराबी वाले स्थान को ढूँढने में काफी समय खर्च करते हुए यह देखा होगा कि कैसे वह फ़्यूज बल्बों को ढूँढने में सभी बल्बों की जाँच करता है, खराब बल्बों को बदलता है। इसके विपरीत पार्श्वक्रम परिपथ में विद्युत धारा विभिन्न वैद्युत साधित्रों में विभाजित हो जाती है। पार्श्व परिपथ में कुल प्रतिरोध समीकरण (11.18) के अनुसार घटता है। यह विशेष रूप से तब अधिक सहायक होता है, जब साधित्रों के प्रतिरोध भिन्न-भिन्न होते हैं तथा उन्हें उचित रूप से कार्य करने के लिए भिन्न विद्युत धारा की आवश्यकता होती है।

चित्र 11.12 श्रेणीक्रम तथा पार्श्वक्रम में संयोजित प्रतिरोधकों के संयोजन को दर्शाता विद्युत परिपथ
प्रश्न
1. जब (a) $1 \Omega$ तथा $10^{6} \Omega$ (b) $1 \Omega, 103 \Omega$ तथा $10^{6} \Omega$ के प्रतिरोध पार्श्वक्रम में संयोजित किए जाते हैं तो इनके तुल्य प्रतिरोध के संबंध में आप क्या निर्णय करेंगे।
Show Answer
#missing2. $100 \Omega$ का एक विद्युत लैम्प, $50 \Omega$ का एक विद्युत टोस्टर तथा $500 \Omega$ का एक जल फिल्टर $220 \mathrm{~V}$ के विद्युत स्रोत से पार्श्वक्रम में संयोजित हैं। उस विद्युत इस्तरी का प्रतिरोध क्या है, जिसे यदि समान स्रोत के साथ संयोजित कर दें तो वह उतनी ही विद्युत धारा लेती है जितनी तीनों युक्तियाँ लेती हैं। यह भी ज्ञात कीजिए कि इस विद्युत इस्तरी से कितनी विद्युत धारा प्रवाहित होती है?
Show Answer
#missing3. श्रेणीक्रम में संयोजित करने के स्थान पर वैद्युत युक्तियों को पार्श्वक्रम में संयोजित करने के क्या लाभ हैं?
Show Answer
#missing4. $2 \Omega, 3 \Omega$ तथा $6 \Omega$ के तीन प्रतिरोधकों को किस प्रकार संयोजित करेंगे कि संयोजन का कुल प्रतिरोध (a) $4 \Omega$, (b) $1 \Omega$ हो?
Show Answer
#missing5. $4 \Omega, 8 \Omega, 12 \Omega$ तथा $24 \Omega$ प्रतिरोध की चार कुंडलियों को किस प्रकार संयोजित करें कि संयोजन से (a) अधिकतम (b) निम्नतम प्रतिरोध प्राप्त हो सके?
Show Answer
#missing11.7 विद्युत धारा का तापीय प्रभाव
हम जानते हैं कि बैटरी अथवा सेल विद्युत ऊर्जा के स्रोत हैं। सेल के भीतर होने वाली रासायनिक अभिक्रिया सेल के दो टर्मिनलों के बीच विभवांतर उत्पन्न करती है, जो बैटरी से संयोजित किसी प्रतिरोधक अथवा प्रतिरोधकों के किसी निकाय में विद्युत धारा प्रवाहित करने के लिए इलेक्ट्रॉनों में गति स्थापित करता है। हमने अनुभाग 11.2 में यह अध्ययन किया है कि परिपथ में विद्युत धारा बनाए रखने के लिए स्रोत को अपनी ऊर्जा खर्च करते रहना पड़ता है। यह ऊर्जा कहाँ चली जाती है? विद्युत धारा बनाए रखने में, खर्च हुई स्रोत की ऊर्जा का कुछ भाग उपयोगी कार्य करने (जैसे पंखे की पंखुड़ियों को घुमाना) में उपयोग हो जाता है। स्रोत की ऊर्जा का शेष भाग उस ऊष्मा को उत्पन्न करने में खर्च होता है, जो साधित्रों के ताप में वृद्धि करती है। इसका प्रेक्षण प्रायः हम अपने दैनिक जीवन में करते हैं, उदाहरण के लिए- हम किसी विद्युत पंखे को निरंतर काफी समय तक चलाते हैं तो वह गर्म हो जाता है। इसके विपरीत यदि विद्युत परिपथ विशुद्ध रूप से प्रतिरोधक है, अर्थात बैटरी से केवल प्रतिरोधकों का एक समूह ही संयोजित है तो स्रोत की ऊर्जा निरंतर पूर्ण रूप से ऊष्मा के रूप में क्षयित होती रहती है। इसे विद्युत धारा का तापीय प्रभाव कहते हैं। इस प्रभाव का उपयोग विद्युत हीटर, विद्युत इस्तरी जैसी युक्तियों में किया जाता है।
प्रतिरोध $R$ के किसी प्रतिरोधक पर विचार कीजिए, जिससे विद्युत धारा I प्रवाहित हो रही है। मान लीजिए इसके सिरों के बीच विभवांतर $V$ (चित्र 11.13) है। मान लीजिए इससे समय $t$ में $Q$ आवेश प्रवाहित होता है। $Q$ आवेश विभवांतर $V$ से प्रवाहित होने में किया गया कार्य $V Q$ है। अतः स्रोत को समय $t$ में $V Q$ ऊर्जा की आपूर्ति करनी चाहिए। अतः स्रोत द्वारा परिपथ में निवेशित शक्ति
$ \begin{equation*} P=V \frac{Q}{t}=V I \tag{11.19} \end{equation*} $
अर्थात समय $t$ में स्रोत द्वारा परिपथ को प्रदान की गई ऊर्जा $\mathrm{P} \times \mathrm{t}$ है, जो $V I t$ के बराबर है। स्रोत द्वारा खर्च की जाने वाली इस ऊर्जा का क्या होता है? यह ऊर्जा ऊष्मा के रूप में प्रतिरोधक में क्षयित हो जाती है। इस प्रकार किसी स्थायी विद्युत धारा $I$ द्वारा समय $t$ में उत्पन्न ऊष्मा की मात्रा
$ \begin{equation*} H=V I t \tag{11.20} \end{equation*} $
ओम का नियम [समीकरण (11.5)] लागू करने पर हमें प्राप्त होता है-
$ \begin{equation*} H=I^{2} R t \tag{11.21} \end{equation*} $
इसे जूल का तापन नियम कहते हैं। इस नियम से यह स्पष्ट है कि किसी प्रतिरोधक में उत्पन्न होने वाली ऊष्मा (i) दिए गए प्रतिरोधक में प्रवाहित होने वाली विद्युत धारा के वर्ग के अनुक्रमानुपाती, (ii) दी गई विद्युत धारा के लिए प्रतिरोध के अनुक्रमानुपाती तथा (iii) उस समय के अनुक्रमानुपाती होती है, जिसके लिए दिए गए प्रतिरोध से विद्युत धारा प्रवाहित होती है। व्यावहारिक परिस्थितियों में जब एक वैद्युत सांधित्र को किसी ज्ञात वोल्टता स्रोत से संयोजित करते हैं तो संबंध $I=V / R$ के द्वारा उस साधित्र से प्रवाहित विद्युत धारा परिकलित करने के पश्चात समीकरण (11.21) का उपयोग करते हैं।

चित्र 11.13 विशुद्ध प्रतिरोधक विद्युत परिपथ में अपरिवर्तनशील विद्युत धारा
उदाहरण 11.10
किसी विद्युत इस्तरी में अधिकतम तापन दर के लिए $840 \mathrm{~W}$ की दर से ऊर्जा उपभुक्त होती है तथा $360 \mathrm{~W}$ की दर से उस समय उपभुक्त होती है, जब तापन की दर निम्नतम है। यदि विद्युत स्रोत की वोल्टता $220 \mathrm{~V}$ है तो दोनों प्रकरणों में विद्युत धारा तथा प्रतिरोध के मान परिकलित कीजिए।
हल
समीकरण (11.19) से हम यह जानते हैं कि निवेशी शक्ति
$P=V I$
इस प्रकार विद्युत धारा $I=P / V$
(a) जब तापन की दर अधिकतम है, तब
$I=840 \mathrm{~W} / 220 \mathrm{~V}=3.82 \mathrm{~A} ;$
तथा विद्युत इस्तरी का प्रतिरोध
$R=V / I=220 \mathrm{~V} / 3.82 \mathrm{~A}=57.60 \Omega$
(b) जब तापन की दर निम्नतम है, तब
$I=360 \mathrm{~W} / 220 \mathrm{~V}=1.64 \mathrm{~A}$;
तथा विद्युत इस्तरी का प्रतिरोध
$R=V / I=220 \mathrm{~V} / 1.64 \mathrm{~A}=134.15 \Omega$
उदाहरण 11.11
किसी $4 \Omega$ प्रतिरोधक से प्रति सेकंड $100 \mathrm{~J}$ ऊष्मा उत्पन्न हो रही है। प्रतिरोधक के सिरों पर विभवांतर ज्ञात कीजिए।
हल
$H=100 \mathrm{~J}, R=4 \Omega, t=1 \mathrm{~s}, V=$ ?
समीकरण (11.21) से हमें प्रतिरोध से प्रवाहित विद्युत धारा $i$ प्राप्त होती है
$I=\sqrt{ }(\mathrm{H} / \mathrm{Rt})$
$=\quad \sqrt{ }[100 \mathrm{~J} /(4 \Omega \times 1 \mathrm{~s})]$
$=\quad 5 \mathrm{~A}$
समीकरण (11.5) से प्रतिरोधक के सिरों पर विभवांतर $V$ प्राप्त होता है
$ \begin{aligned} V & =I R \\ & =5 A \times 4 \Omega \\ & =20 V . \end{aligned} $
प्रश्न
1. किसी विद्युत हीटर की डोरी क्यों उत्तप्त नहीं होती, जबकि उसका तापन अवयव उत्तप्त हो जाता है?
Show Answer
#missing2. एक घंटे में $50 \mathrm{~W}$ विभवांतर से 96000 कूलॉम आवेश को स्थानांतरित करने में उत्पन्न ऊष्मा परिकलित कीजिए।
Show Answer
#missing3. $20 \Omega$ प्रतिरोध की कोई विद्युत इस्तरी $5 \mathrm{~A}$ विद्युत धारा लेती है। $30 \mathrm{~s}$ में उत्पन्न ऊष्मा परिकलित कीजिए।
Show Answer
#missing11.7.1 विद्युत धारा के तापीय प्रभाव के व्यावहारिक अनुप्रयोग
किसी चालक में ऊष्मा उत्पन्न होना विद्युत धारा का अवश्यंभावी परिणाम है। बहुत-सी स्थितियों में यह अवांछनीय होता है, क्योंकि वह उपयोगी विद्युत ऊर्जा को ऊष्मा में रूपांतरित कर देता है। विद्युत परिपथों में अपरिहार्य तापन, परिपथ के अवयवों के ताप में वृद्धि कर सकता है, जिससे उनके गुणों में परिवर्तन हो सकता है। विद्युत इस्तरी, विद्युत टोस्टर, विद्युत तंदूर, विद्युत केतली तथा विद्युत हीटर जूल के तापन पर आधारित कुछ सुपरिचित युक्तियाँ हैं।
विद्युत तापन का उपयोग प्रकाश उत्पन्न करने में भी होता है, जैसा कि हम विद्युत बल्ब में देखते हैं। यहाँ पर बल्ब के तंतु को उत्पन्न ऊष्मा को जितना संभव हो सके रोके रखना चाहिए ताकि वह अत्यंत तप्त होकर प्रकाश उत्पन्न करे। इसे इतने उच्च ताप पर पिघलना नहीं चाहिए। बल्ब के तंतुओं को बनाने के लिए टंगस्टन (गलनांक $3380^{\circ} \mathrm{C}$ ) का उपयोग किया जाता है, जो उच्च गलनांक की एक प्रबल धातु है। विद्युतरोधी टेक का उपयोग करके तंतु को यथासंभव ताप विलगित बनाना चाहिए। प्रायः बल्बों में रासायनिक दृष्टि से अक्रिय नाइट्रोजन तथा आर्गन गैस भरी जाती है, जिससे उसके तंतु की आयु में वृद्धि हो जाती है। तंतु द्वारा उपभुक्त ऊर्जा का अधिकांश भाग ऊष्मा के रूप में प्रकट होता है, परंतु इसका एक अल्प भाग विकरित प्रकाश के रूप में भी दृष्टिगोचर होता है।
जूल तापन का एक और सामान्य उपयोग विद्युत परिपथों में उपयोग होने वाला फ्यूज है। यह परिपथों तथा साधित्रों की सुरक्षा, किसी भी अनावश्यक रूप से उच्च विद्युत धारा को उनसे प्रवाहित न होने देकर, करता है। फ्यूज़ को युक्ति के साथ श्रेणीक्रम में संयोजित करते हैं। फ्यूज़ किसी ऐसी धातु अथवा मिश्रातु के तार का टुकड़ा होता है, जिसका उचित गलनांक हो, उदाहरण के लिए- ऐलुमिनियम, कॉपर, आयरन, लैड आदि। यदि परिपथ में किसी निर्दिष्ट मान से अधिक मान की विद्युत धारा प्रवाहित होती है तो फ्यूज़ तार के ताप में वृद्धि होती है। इससे फ्यूज़ तार पिघल जाता है और परिपथ टूट जाता है। फ्यूज़ तार प्रायः धातु के सिरे वाले पोर्सेलेन अथवा इसी प्रकार के विद्युतरोधी पदार्थ के कार्ट्रिज में रखा जाता है। घरेलू परिपथों में उपयोग होने वाली फ्यूज़ की अनुमत विद्युत धारा $1 \mathrm{~A}, 2 \mathrm{~A}, 3 \mathrm{~A}, 5 \mathrm{~A}, 10 \mathrm{~A}$ आदि होती है। उस विद्युत इस्तरी के परिपथ में जो $1 \mathrm{~kW}$ की विद्युत शक्ति उस समय उपभुक्त करती है, जब उसे $220 \mathrm{~V}$ पर प्रचालित करते हैं, $1000 \mathrm{~W} / 220 \mathrm{~V}=4.54 \mathrm{~A}$ की विद्युत धारा प्रवाहित होती है। इस प्रकरण में $5 \mathrm{~A}$ अनुमतांक का फ्यूज उपयोग किया जाना चाहिए।
11.8 विद्युत शक्ति
आपने अपनी पिछली कक्षाओं में यह अध्ययन किया था कि कार्य करने की दर को शक्ति कहते हैं। ऊर्जा के उपभुक्त होने की दर को भी शक्ति कहते हैं।
समीकरण (11.21) से हमें किसी विद्युत परिपथ में उपभुक्त अथवा क्षयित विद्युत ऊर्जा की दर प्राप्त होती है। इसे विद्युत शक्ति भी कहते हैं। शक्ति $P$ को इस प्रकार व्यक्त करते हैं-
$ \begin{aligned} & P=V I \\ \text{ अथवा } & P=I^{2} R=V^{2} / R \end{aligned} $
विद्युत शक्ति का SI मात्रक वाट $(\mathrm{W})$ है। यह उस युक्ति द्वारा उपभुक्त शक्ति है, जिससे उस समय $1 \mathrm{~A}$ विद्युत धारा प्रवाहित होती है, जब उसे $1 \mathrm{~V}$ विभवांतर पर प्रचालित कराया जाता है। इस प्रकार-
$1 \mathrm{~W}=1$ वोल्ट $\times 1$ ऐम्पियर $=1 \mathrm{~V} \mathrm{~A}$
‘वाट’ शक्ति का छोटा मात्रक है। अतः वास्तविइसे भी जानिया!ड़े मात्रक (किलोवाट) का उपयोग करते हैं। एक किलोवाट, 1000 वाट के बराबर होता है। चूँकि विद्युत ऊर्जा शक्ति तथा समय का गुणनफल होती है इसलिए विद्युत ऊर्जा का मात्रक वाट घंटा $(\mathrm{Wh})$ है। जब एक वाट शक्ति का उपयोग 1 घंटे तक होता है तो उपभुक्त ऊर्जा एक वाट घंटा होती है। विद्युत ऊर्जा का व्यापारिक मात्रक किलोवाट घंटा $(\mathrm{kW} \mathrm{h})$ है, जिसे सामान्य बोलचाल में ‘यूनिट’ कहते हैं।
$ 1 \mathrm{kWh} = 1000 \text { वाट } \times 3600 \text { सेकंड } $
$ =3.6 \times 10^{6} \text { वाट सेकंड } $
$ =3.6 \times 10^{6} \text { जूल }(\mathrm{J})$
यह भी जानिया!
बहुत से लोग यह सोचते हैं कि किसी विद्युत परिपथ में इलेक्ट्रॉन उपभुक्त होते हैं। यह गलत है! हम विद्युत बोर्ड अथवा विद्युत कंपनी को विद्युत बल्ब, विद्युत पंखे तथा इंजन आदि जैसे विद्युत साधित्रों से इलेक्ट्रॉनों को गति देने के लिए प्रदान की जाने वाली विद्युत ऊर्जा का भुगतान करते हैं। हम अपने द्वारा उपभुक्त ऊर्जा के लिए भुगतान करते हैं।
उदाहरण 11.12
कोई विद्युत बल्ब $220 \mathrm{~V}$ के जनित्र से संयोजित है। यदि बल्ब से $0.50 \mathrm{~A}$ विद्युत धारा प्रवाहित होती है तो बल्ब की शक्ति क्या है?
हल
$ \begin{aligned} P & =V I \\ & =220 \mathrm{~V} \times 0.50 \mathrm{~A} \\ & =110 \mathrm{~J} / \mathrm{s} \\ & =110 \mathrm{~W} \end{aligned} $
उदाहरण 11.13
$400 \mathrm{~W}$ अनुमत का कोई विद्युत रेफ्रिजरेटर 8 घंटे/दिन चलाया जाता है। 3.00 रुपये प्रति $\mathrm{kWh}$ की दर से इसे 30 दिन तक चलाने के लिए ऊर्जा का मूल्य क्या है?
हल
30 दिन में रेफ्रिजरेटर द्वारा उपभुक्त कुल ऊर्जा
$400 \mathrm{~W} \times 8.0$ घंटे/दिन $\times 30$ दिन $=96000 \mathrm{~W} \mathrm{~h}$
$=96 \mathrm{kWh}$
इस प्रकार 30 दिन तक रेफ्रिजरेटर को चलाने में उपभुक्त कुल ऊर्जा का मूल्य $96 \mathrm{~kW} \mathrm{~h} \times 3.00 \mathrm{~kW}$ h रुपये $=288.00$ रुपये
प्रश्न
1. विद्युत धारा द्वारा प्रदत्त ऊर्जा की दर का निर्धारण कैसे किया जाता है?
Show Answer
#missing2. कोई विद्युत मोटर $220 \mathrm{~V}$ के विद्युत स्रोत से $5.0 \mathrm{~A}$ विद्युत धारा लेता है। मोटर की शक्ति निर्धारित कीजिए तथा 2 घंटे में मोटर द्वारा उपभुक्त ऊर्जा परिकलित कीजिए।
Show Answer
#missingआपने क्या सीखा
- किसी चालक में गतिशील इलेक्ट्रॉनों की धारा विद्युत धारा की रचना करती है। परिपाटी के अनुसार इलेक्ट्रॉनों के प्रवाह की दिशा के विपरीत दिशा को विद्युत धारा की दिशा माना जाता है।
- विद्युत धारा का SI मात्रक ऐम्पियर $(\mathrm{A})$ है।
- किसी विद्युत परिपथ में इलेक्ट्रॉनों को गति प्रदान करने के लिए हम किसी सेल अथवा बैटरी का उपयोग करते हैं। सेल अपने सिरों के बीच विभवांतर उत्पन्न करता है। इस विभवांतर को वोल्ट $(\mathrm{V})$ में मापते हैं।
- प्रतिरोध एक ऐसा गुणधर्म है, जो किसी चालक में इलेक्ट्रॉनों के प्रवाह का विरोध करता है। यह विद्युत धारा के परिमाण को नियंत्रित करता है। प्रतिरोध का SI मात्रक ओम $(\Omega)$ है।
- ओम का नियम- किसी प्रतिरोधक के सिरों के बीच विभवांतर उसमें प्रवाहित विद्युत धारा के अनुक्रमानुपाती होता है, परंतु एक शर्त यह है कि प्रतिरोधक का ताप समान रहना चाहिए।
- किसी चालक का प्रतिरोध उसकी लंबाई पर सीधे उसकी अनुप्रस्थ काट के क्षेत्रफल पर प्रतिलोमतः निर्भर करता है और उस पदार्थ की प्रकृति पर भी निर्भर करता है, जिससे वह बना है।
- श्रेणीक्रम में संयोजित बहुत से प्रतिरोधकों का तुल्य प्रतिरोध उनके व्यष्टिगत प्रतिरोधों के योग के बराबर होता है।
- पार्श्वक्रम में संयोजित प्रतिरोधकों के समुच्चय का तुल्य प्रतिरोध $R _{p}$ निम्नलिखित संबंध द्वारा व्यक्त किया जाता है$\frac{1}{R _{p}}=\frac{1}{R _{1}}+\frac{1}{R _{2}}+\frac{1}{R _{3}}+\ldots$
- किसी प्रतिरोधक में क्षयित अथवा उपभुक्त ऊर्जा को इस प्रकार व्यक्त किया जाता है$W=V \times I \times T$
- विद्युत शक्ति का मात्रक वाट $(\mathrm{W})$ है। जब $1 \mathrm{~A}$ विद्युत धारा $1 \mathrm{~V}$ विभवांतर पर प्रवाहित होती है तो परिपथ में उपभुक्त शक्ति 1 वाट होती है।
- विद्युत ऊर्जा का व्यापारिक मात्रक किलोवाट घंटा $(\mathrm{kW} \mathrm{h})$ है- $1 \mathrm{kWh}=3,600,000 \mathrm{~J}=3.6 \times 10^{6} \mathrm{~J}$
अभ्यास
1. प्रतिरोध $R$ के किसी तार के टुकड़े को पाँच बराबर भागों में काटा जाता है। इन टुकड़ों को फिर पार्श्रक्रम में संयोजित कर देते हैं। यदि संयोजन का तुल्य प्रतिरोध $R^{\prime}$ है तो $R / R^{\prime}$ अनुपात का मान क्या है-
(a) $1 / 25$
(b) $1 / 5$
(c) $5$
(d) $25$
Show Answer
#missing2. निम्नलिखित में से कौन-सा पद विद्युत परिपथ में विद्युत शक्ति को निरूपित नहीं करता?
(a) $I^{2} R$
(b) $I R^{2}$
(c) $V I$
(d) $V^{2} / R$
Show Answer
#missing3. किसी विद्युत बल्ब का अनुमंताक $220 \mathrm{~V} ; 100 \mathrm{~W}$ है। जब इसे $110 \mathrm{~V}$ पर प्रचालित करते हैं तब इसके द्वारा उपभुक्त शक्ति कितनी होती है?
(a) $100 \mathrm{~W}$
(b) $75 \mathrm{~W}$
(c) $50 \mathrm{~W}$
(d) $25 \mathrm{~W}$
Show Answer
#missing4. दो चालक तार जिनके पदार्थ, लंबाई तथा व्यास समान हैं, किसी विद्युत परिपथ में पहले श्रेणीक्रम में और फिर पार्श्रक्रम में संयोजित किए जाते हैं। श्रेणीक्रम तथा पार्शक्रम संयोजन में उत्पन्न ऊष्माओं का अनुपात क्या होगा?
(a) $1: 2$
(b) $2: 1$
(c) $1: 4$
(d) $4: 1$
Show Answer
#missing5. किसी विद्युत परिपथ में दो बिंदुओं के बीच विभवांतर मापने के लिए वोल्टमीटर को किस प्रकार संयोजित किया जाता है?
Show Answer
#missing6. किसी ताँबे के तार का व्यास $0.5 \mathrm{~mm}$ तथा प्रतिरोधकता $1.6 \times 10^{-8} \Omega \mathrm{m}$ है। $10 \Omega$ प्रतिरोध का प्रतिरोधक बनाने के लिए कितने लंबे तार की आवश्यकता होगी? यदि इससे दोगुने व्यास का तार लें तो प्रतिरोध में क्या अंतर आएगा?
Show Answer
#missing7. किसी प्रतिरोधक के सिरों के बीच विभवांतर $\mathrm{V}$ के विभिन्न मानों के लिए उससे प्रवाहित विद्युत धाराओं $I$ के संगत मान आगे दिए गए हैं-
| $I$ (ऐम्पियर) | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 |
| $V$ (वोल्ट) | 1.6 | 3.4 | 6.7 | 10.2 | 13.2 |
$V$ तथा $I$ के बीच ग्राफ खींचकर इस प्रतिरोधक का प्रतिरोध ज्ञात कीजिए।
Show Answer
#missing8. किसी अज्ञात प्रतिरोध के प्रतिरोधक के सिरों से $12 \mathrm{~V}$ की बैटरी को संयोजित करने पर परिपथ में $2.5 \mathrm{~mA}$ विद्युत धारा प्रवाहित होती है। प्रतिरोधक का प्रतिरोध परिकलित कीजिए।
Show Answer
#missing9. $9 \mathrm{~V}$ की किसी बैटरी को $0.2 \Omega, 0.3 \Omega, 0.4 \Omega, 0.5 \Omega$ तथा $12 \Omega$ के प्रतिरोधकों के साथ श्रेणीक्रम में संयोजित किया गया है। $12 \Omega$ के प्रतिरोधक से कितनी विद्युत धारा प्रवाहित होगी?
Show Answer
#missing10. $176 \Omega$ प्रतिरोध के कितने प्रतिरोधकों को पार्श्रक्रम में संयोजित करें कि $220 \mathrm{~V}$ के विद्युत स्रोत से संयोजन से $5 \mathrm{~A}$ विद्युत धारा प्रवाहित हो?
Show Answer
#missing11. यह दर्शाइए कि आप $6 \Omega$ प्रतिरोध के तीन प्रतिरोधकों को किस प्रकार संयोजित करेंगे कि प्राप्त संयोजन का प्रतिरोध (i) $9 \Omega$, (ii) $4 \Omega$ हो।
Show Answer
#missing12. $220 \mathrm{~V}$ की विद्युत लाइन पर उपयोग किए जाने वाले बहुत से बल्बों का अनुमतांक $10 \mathrm{~W}$ है। यदि $220 \mathrm{~V}$ लाइन से अनुमत अधिकतम विद्युत धारा $5 \mathrm{~A}$ है तो इस लाइन के दो तारों के बीच कितने बल्ब पार्श्वक्रम में संयोजित किए जा सकते है?
Show Answer
#missing13. किसी विद्युत भट्टी की तप्त प्लेट दो प्रतिरोधक कुंडलियों $A$ तथा $B$ की बनी हैं, जिनमें प्रत्येक का प्रतिरोध 24 $\Omega$ है तथा इन्हें पृथक-पृथक, श्रेणीक्रम में अथवा पार्श्वक्रम में संयोजित करके उपयोग किया जा सकता है। यदि यह भट्टी $220 \mathrm{~V}$ विद्युत स्रोत से संयोजित की जाती है तो तीनों प्रकरणों में प्रवाहित विद्युत धाराएँ क्या हैं?
Show Answer
#missing14. निम्ललिखित परिपथों में प्रत्येक में $2 \Omega$ प्रतिरोधक द्वारा उपभुक्त शक्तियों की तुलना कीजिए:- (i) $6 \mathrm{~V}$ की बैटरी से संयोजित $1 \Omega$ तथा $2 \Omega$ श्रेणीक्रम संयोजन (ii) $4 \mathrm{~V}$ बैटरी से संयोजित $12 \Omega$ तथा 2 $\Omega$ का पार्श्वक्रम संयोजन।
Show Answer
#missing15. दो विद्युत लैम्प जिनमें से एक का अनुमतांक $100 \mathrm{~W} ; 220 \mathrm{~V}$ तथा दूसरे का $60 \mathrm{~W} ; 220 \mathrm{~V}$ है, विद्युत मेंस के साथ पार्श्रक्रम में संयोजित है। यदि विद्युत आपूर्ति की वोल्टता $220 \mathrm{~V}$ है तो विद्युत मेंस से कितनी धारा ली जाती है?
Show Answer
#missing16. किसमें अधिक विद्युत ऊर्जा उपभुक्त होती है- $250 \mathrm{~W}$ का टी.वी. सेट जो एक घंटे तक चलाया जाता है अथवा $120 \mathrm{~W}$ का विद्युत हीटर, जो 10 मिनट के लिए चलाया जाता है?
Show Answer
#missing17. $8 \Omega$ प्रतिरोध का कोई विद्युत हीटर विद्युत मेंस से 2 घंटे तक $15 \mathrm{~A}$ विद्युत धारा लेता है। हीटर में उत्पन्न ऊष्मा की दर परिकलित कीजिए।
Show Answer
#missing18. निम्नलिखित को स्पष्ट कीजिए-
(a) विद्युत लैम्पों के तंतुओं के निर्माण में प्रायः एकमात्र टंगस्टन का ही उपयोग क्यों किया जाता है?
(b) विद्युत तापन युक्तियों जैसे ब्रेड-टोस्टर तथा विद्युत इस्तरी के चालक शुद्ध धातुओं के स्थान पर मिश्रातुओं के क्यों बनाए जाते हैं?
(c) घरेलू विद्युत परिपथों में श्रेणीक्रम संयोजन का उपयोग क्यों नहीं किया जाता है?
(d) किसी तार का प्रतिरोध उसकी अनुप्रस्थ काट के क्षेत्रफल में परिवर्तन के साथ किस प्रकार परिवर्तित होता है?
(e) विद्युत संचारण के लिए प्रायः कॉपर तथा ऐलुमिनियम के तारों का उपयोग क्यों किया जाता है?










