wave-optics Question 1
Question: Q. 1. Consider a ray of light incident from air onto a slab of glass (refractive index $n$ ) of width $d$, at an angle $\theta$. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
(a) $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{\frac{1}{2}}+\pi$.
(b) $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{\frac{1}{2}}$.
(c) $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{\frac{1}{2}}+\frac{\pi}{2}$.
(d) $\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{\frac{1}{2}}+2 \pi$.
Show Answer
Solution:
Ans. Correct option : (a)
Explanation: If slab of a glass is placed in air, the wave reflected from the upper surface (from a denser medium) suffers a sudden phase change of $\pi$, while the wave reflected from the lower surface (from a rarer medium) suffers no such phase change.
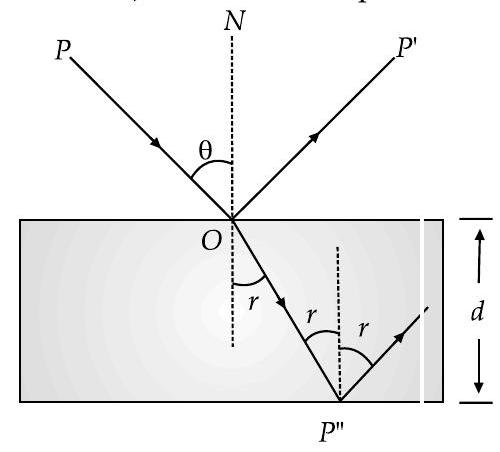
Now consider the diagram, the ray $(P O)$ is incident at an angle $\theta$ and gets reflected in the direction $P^{\prime}$ and refracted in the direction $P^{\prime \prime}$. Due to reflection from the glass medium, there is a phase change of $\pi$.
Time taken to travel along $O P^{\prime \prime}$,
$\Delta t=\frac{O P^{\prime \prime}}{v}=\frac{\frac{d}{\cos r}}{\frac{c}{n}}=\frac{n d}{c \times \cos r}$
From Snell’s law, $n=\frac{\sin \theta}{\sin r}$
$$ \begin{aligned} \sin r & =\frac{\sin \theta}{n} \ \cos r & =\sqrt{1-\sin ^{2} r} \ & =\sqrt{1-\frac{\sin ^{2} \theta}{n^{2}}} \end{aligned} $$
Phase difference,
$$ \begin{aligned} \Delta \phi & =\frac{2 \pi}{T} \times \Delta t \ \Rightarrow \Delta \phi & =\frac{2 \pi n d}{\lambda}\left(1-\frac{\sin ^{2} \theta}{n^{2}}\right)^{\frac{-1}{2}} \end{aligned} $$
So, net phase difference $=\Delta f+\pi$
$$ \Rightarrow \quad \Delta \phi_{\text {net }}=\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^{2}} \sin ^{2} \theta\right)^{\frac{1}{2}}+\pi $$
Very Short Answer Type Questions
(1 mark each)
