ray-optics-and-optical-instruments Question 15
Question: Q. 2. (i) Prove that for a concave mirror, the radius of curvature is twice the focal length for small aperture as compare to its radius of curvature.
(ii) With the help of a suitable diagram, derive the mirror formula for a concave mirror. A [CBSE 2011, 2009]
Show Answer
Solution:
Ans. (i)
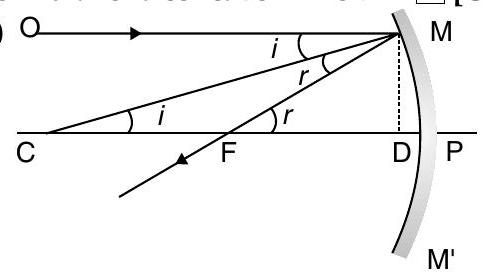
Let us consider
Hence
So,
Since aperture of mirror is very small,
(ii) Try yourself Similar Q. 1 (ii) Long Answer Type Question.
TOPIC-2
Refraction through Glass Slab, Prism and Lenses and Total Internal Reflection
Revision Notes
Refraction of light : Refraction is deviation of light when it obliquely travels from one medium to another medium. Snell experimentally found the following laws of refractions.
Laws of Refraction of Light
- The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the sameplane.
The ratio of sine of ang of incidence to the sine of angle of refraction is a constant, for the light of a given colour and for the given pair of media. This constant value is called the refractive index of the second medium with respect to the first medium.
This is known as Snell’s law.
From Snell’s law
It shows that if
- If the first medium is air, then this refractive index is known as the absolute refractive index of the second medium. The absolute refractive index of a medium is expressed by
If light ray enters from one medium to another medium in such a way that bending of light is away from normal then second medium is optically rarer than the first medium. If bending of light is towards normal then second medium is optically denser than the first medium.
Principle of Reversibility
According to the principle of reversibility, the path of light is reversible even if it is going through several media. It means light follows exactly the same path when its direction is reversed.
Applying this rule we may find that if light travels through several media say medium 1 to medium 2 and then to medium 3 then to medium 1 .
Though refraction rules are universal but direction of emergent ray depends upon the shape of the medium or in other words shape and angle between incident and emergent interfaces (refracting surfaces).
Refraction through glass slab
- Emergent ray is parallel to the incident ray but it does suffer lateral displacement.
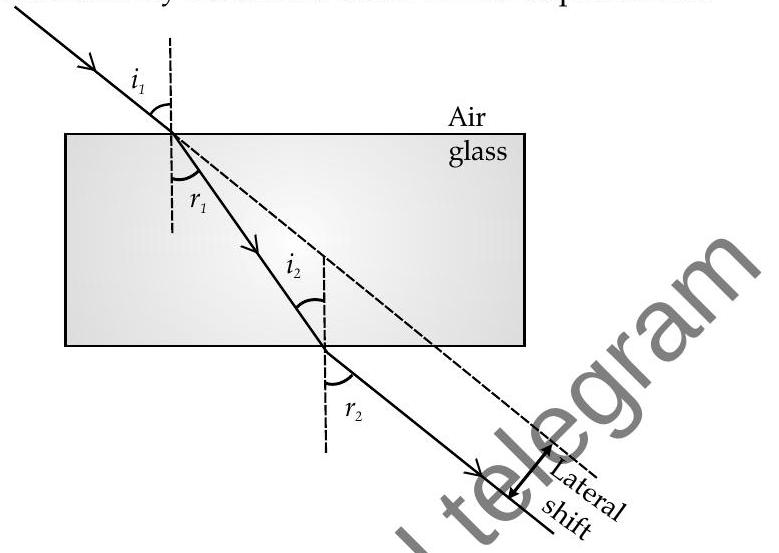
The apparent depth of the object is always less than actuatdepth when looking through glass or water .
Here,
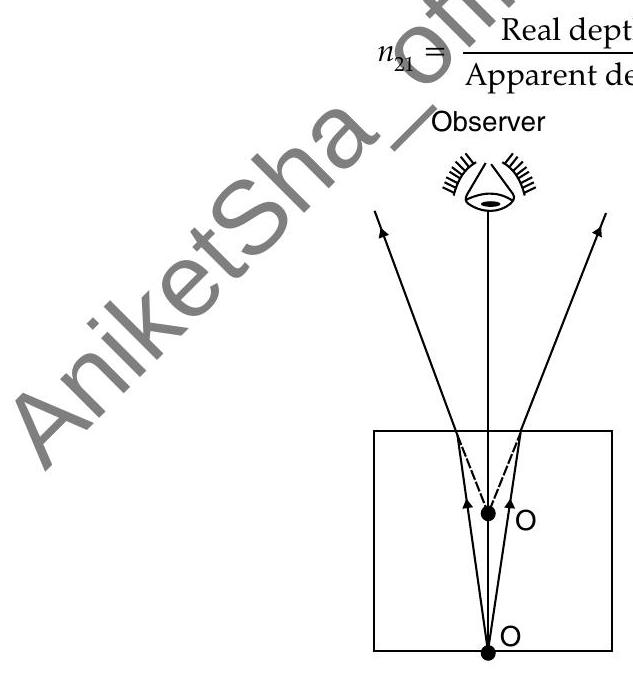
Following phenomena occur due to the refraction of light.
- Bottom of surface of water pool seems to be raised.
- The letter appears to be raised when we seeing it through a glass slab
- Object looks bigger than its actual size and raised when we dip it into liquid.
- Twinkling of stars
- Delayed sunset and early sunrise
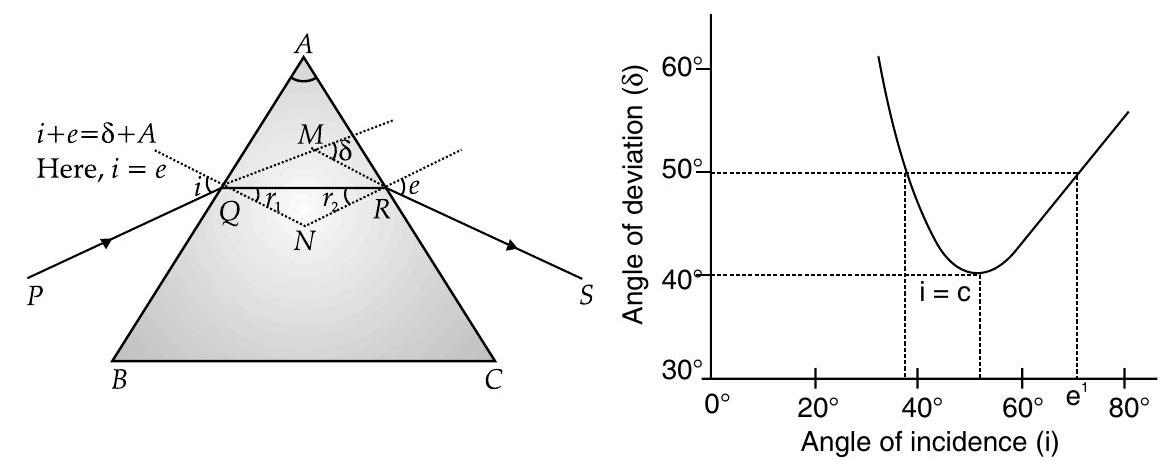
Refraction through Prism
In prism, refracting surfaces are planes but inclined to each other.
Defracting ray always bends towards the base.
Angle of deviation,
Angle of minimum deviation : When incident angle is increased gradually the angle of deviation initially decreases, and after obtaining a minimum value, it starts increasing again. This minimum deviation is called angle of minimum deviation
.
(i)
(ii)
- At minimum deviation stage it is observed that angle of
As angle of prism and deviation can be found experimentally, this equation is used to determine the refractive index of the material of prism.
For thin prism,
. This equation implies that thin prisms do not deviate light much.
When light travels from an optically denser medium to a rarer medium at the interface, sometime it is reflected into the same medium. This reflection is called the internal reflection.
- Critical angle is that value of incident angle for which angle of refraction is
(where,
- If the incidence angle is more than the critical angle, refraction is not possible and incident ray reflects in denser medium. This is known as total internal reflection.
Hence, conditions for total infernal reflection are :
- Incident ray is in densermedium.
- Angle of incidenceshould be larger than critical angle.
Natural phenomenonbased upon total internal reflection
- Mirage : On hot summer days, light from tall objects successively bends away from the normal due to gradual air density decrease towards the earth. This results total internal reflection and formation of inverted images of distant tall objects. It causes an optical illusion to the observer. This phenomenon is called mirage.
- Brilliance of diamond : Refractive index of diamond is very high
Applications of total internal reflection :
- In optical fibers for optical communication.
- Prism : Prisms designed to bend light by
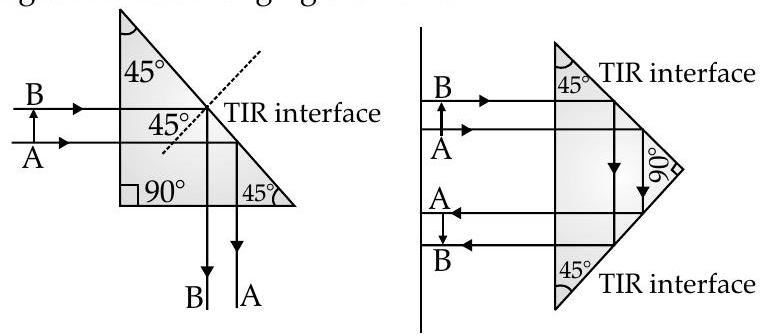
TIR
Refraction at spherical surface: If the rays are incident from a medium of refractive index
, to another medium of refractive index , the formula comes out to be
Where,
D Lens : A lens is a piece of transparent glass which is bounded by two surfaces out of which at least one surface is spherical.
There are two types of lenses
- Convex lens : A convex lens is one which is thinner at sides and thick at centre.
- Concave lens : A concave lens is one which is thicker at sides and thin at centre.
Relation between object distance, image distance with focal length of lens :
The relation can be expressed as
Magnification by lens :
Power of a lens :
The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter
The SI unit of power is diopter when focal length is in metre. It is denoted by
- When two or more lenses are combined then the power of combined lens is sum of individual power of lenses.
Lens maker’s Formula :
| Position of the image | Relative size of the image | Nature of the image | |
|---|---|---|---|
| At infinity | at focus |
Highly diminished point sized | Real and inverted |
| Beyond |
Between |
Diminished | Real and inverted |
| At |
at |
Same sized | Real and inverted |
| Between |
Beyond |
Enlarged | Real and inverted |
| At Focus |
At infinity | Infinitely enlarged | Real and inverted |
| Between focus optical centre |
On the same side of the lens as object |
Enlarged | Virtual and Erect |
Power of a lens,
So, the above formula is used to make lenses of required power. Hence this formula is known as lens maker’s formula.
- Image formation in convex lens for different positions of object
- Image formation in concave lens for different positions of object
| Position of the object | Position of the image | Relative size of the image | Nature of the image |
|---|---|---|---|
| At infinity | At focus |
Highly diminished point sized | Virtual and Erect |
| Between infinity and the optical center lens |
Between focus optical center |
Diminished | Virtual and Erect |
Dispersion of white light through Prism : Splitting of white colour into its constituent colours is known as dispersion of light. This is due to different colours having different deviations.
- The seven colours are violet, indigo, blue, green, yellow, orange and red. The acronym of this colour band is VIBGYOR.
- Different colours of light have different wavelengths and different frequency in medium. This is the cause of dispersion.
- In vacuum, the speed of light is independent of wavelength. Thus, vacuum (or air approximately) is a nondispersive medium in which all colours travel with the same speed. This also follows from the fact that sunlight reaches us in the form of white light (combination of all colours) and not as its components in day (noon) time. On the other hand, glass is a dispersive medium.
- Angular dispersion through thin prism
- Power of dispersion,
- Recombination of white light : If we place an inverted identical prism after the first prism, all components colours of light recombine and again became a beam of white light.
Phenomenon related to dispersion of light :
- Formation of Rainbow : Rainbow is the natural phenomenon of disperson of light. After a rain shower when sky becomes clear and sunny, we may observe a rainbow in a direction opposite to the direction of sun when sun is at our backside. It is caused due to the combined effect of refraction, total internal reflection and dispersion of sunlight by the raindrops suspended in the air.
- In primary rainbow, there is only single total internal refle tionbefore different colours reach observer’s eye. In this rainbow, observer see red colour at top and violetat bottom.
- In secondary rainbow, there are two total internal reffections before different colours reach observer’s eye. In this rainbow, observer see violet colour at top and red at bottom.
- Secondary rainbow is higher
- Intensity of secondary rainbow is lower than the primary rainbow.
Scattering of light : When light deviates randomly from its path due to its interaction with small particles, it is known as scattering of light.
Tyndall Effect : The Tyndall effect is the scattering of light as a beam of light passes through a colloid. The individual suspension particles $$$ catter and reflect light, making the beam visible.
The colour of the scattered light depends on the size of the scattering particles.
For
, where, is the size of scattering particle, one has Rayleigh scattering which is proportional to . For , i.e., large scattening objects (for example, raindrops, large dust particles); all wavelengths are scattered nearly equally.
Phenomenon related to scattering of light :
- Colour of the clear sky is blue.
- Reddening of the Sun at sunrise and sunset.
- White appearance of Clouds.
Principal focus : Incident ray parallel to the principal axis, after refraction from lens either converge to a point (in case of convex lens) after the lens or appear to diverge from a point (in case of concave lens) before the lens. This point is called the principal focus of the lens.
Know the Formulae
Snell’s law of refraction
Deviation through prism
For thin prism,
Relation between refractive index, angle of prism and minimum deviation
Condition for Total internal reflection are
- Incident ray is in denser medium.
- Angle of incident should be larger than critical angle.
Dor lens
Power of lens
When two or more lenses are combined then the power of combined lens is
sum of individual power of lenses.
- $\mathrm{P}=\mathrm{P}{1}+\mathrm{P}{2}+\ldots .$.
Lens maker’s Formula
$$ \frac{1}{f}=\left(n_{21}-1\right)\left(\frac{1}{\mathcal{H}{1}}-\frac{1}{R{2}}\right) $$
Angular dispersion through thin prism
.
Power of dispersion