Solution:

Ans. Using mirror formula

$$ \frac{1}{v}+\frac{1}{u}=\frac{1}{f} $$

For plane mirror $f=\infty$

Hence

$$ \begin{equation*} \frac{1}{v}+\frac{1}{u}=0 \tag{1} \end{equation*} $$

So, $\quad v=-u$

It means the image sat equal distance and in opposite side of object. This is the true condition in image formation through plane mirror. Hence spherical mirror formula holds equally to a plane mirror. $\mathbf{1}$

Long Answer Type Questions

AI Q. 1.(i) Draw a ray diagram to show image formation when the concave mirror produces a real, inverted and magnified image of the object.

(ii) Obtain the mirror formula and write the expression for the linear magnification.

(iii) Explain two advantages of a reflecting telescope over a refracting telescope.

A [Delhi& O.D. 2018]

Ans. (i) Ray diagram to show the required image formation

(ii) Derivation of mirror formula Expression for linear magnification

iii) Two advantages of a reflecting telescope over a refracting telescope

$1 / 2+1 / 2$

(i)

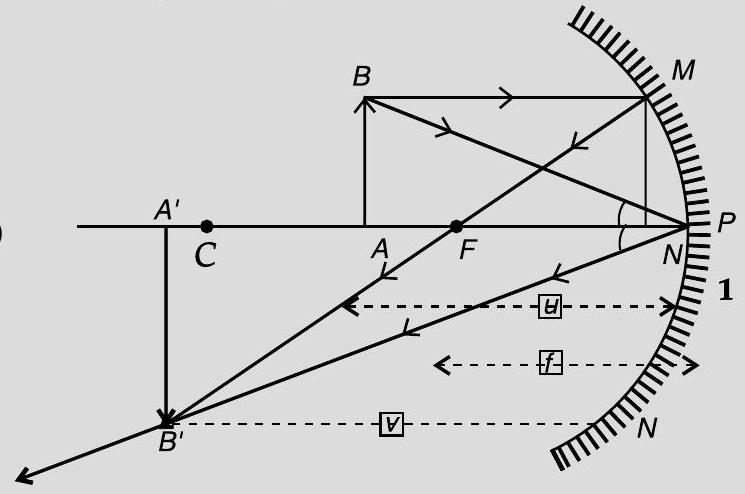
(ii) In the above figure $\triangle B A P$ and $\triangle B^{\prime} A^{\prime} P$ are similar

$$ \begin{equation*} \Rightarrow \quad \frac{B A}{B^{\prime} A^{\prime}}=\frac{P A}{P A^{\prime}} \tag{i} \end{equation*} $$

Similarly, $\triangle M N F$ and $\triangle B^{\prime} A^{\prime} F$ are similar

$$ \begin{equation*} \Rightarrow \quad \frac{M N}{B^{\prime} A^{\prime}}=\frac{N F}{F A^{\prime}} \tag{ii} \end{equation*} $$

$$ \begin{aligned} M N & =B A \ N F & \approx P F \ F A^{\prime} & =P A^{\prime}-P F \end{aligned} $$

$\therefore$ Equation (ii) takes the following form

$$ \begin{equation*} \frac{B A}{B^{\prime} A^{\prime}}=\frac{P F}{P A^{\prime}-P F} \tag{iii} \end{equation*} $$

Using equation (i) and (iii)

$$ \frac{P A}{P A^{\prime}}=\frac{P F}{P A^{\prime}-P F} $$

For the given figure, as per the sign convention,

$$ \begin{aligned} P A & =-u \ P A^{\prime} & =-v \ P F & =-f \ \Rightarrow \quad \frac{-u}{-v} & =\frac{-f}{-v-(-f)} \ \frac{u}{v} & =\frac{f}{v-f} \ u v-u f & =v f \end{aligned} $$

Dividing each term by $u v f$, we get

$$ \begin{aligned} \frac{1}{f}-\frac{1}{v} & =\frac{1}{u} \ \Rightarrow \quad \frac{1}{f} & =\frac{1}{v}+\frac{1}{u} \end{aligned} $$

Linear magnification $=-\frac{-v}{u}$,

$$ \text { (alternatively, } m=\frac{h_{i}}{h_{0}} \text { ) } 1 / 2 $$

(iii) Advantages of reflecting telescope over refracting telescope

(i) Mechanical support is easier

$1 / 2+1 / 2$

(ii) Magnifying power is large

(iii) Resolving power is large

(iv) Spherical aberration is reduced

(v) Free from chromatic aberration

(any two)

[CBSE Marking Scheme 2018]