ray-optics-and-optical-instruments Question 12
Question: Q. 1. (a) With the help of a ray diagram, show how a concave mirror is used to obtain an erect and magnified image of an object. (b) Using the above ray diagram, obtain the mirror formula and the expression for linear magnification.
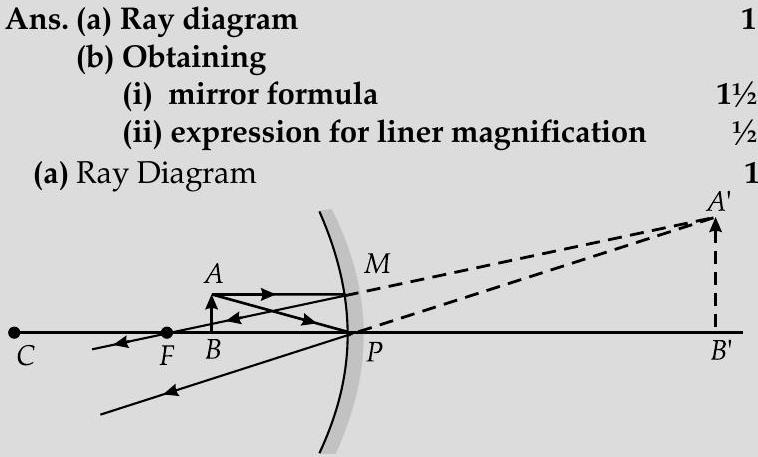
From similar triangles $A^{\prime} B^{\prime} F$ and $M P F$, we have
$$ \begin{aligned} \frac{B^{\prime} A^{\prime}}{P M} & =\frac{B^{\prime} F}{F P} \ \text { or } \quad \frac{B^{\prime} A^{\prime}}{B A} & =\frac{B^{\prime} F}{F P} \quad(\text { Since } P M=B A) \end{aligned} $$
From similar triangles $A^{\prime} B^{\prime} P$ and $A B P$, we have
$$ \frac{B^{\prime} A^{\prime}}{B A}=\frac{B^{\prime} P}{B P} $$
Hence,
$$ \frac{B^{\prime} F}{F P}=\frac{B^{\prime} P}{B P} $$
Now,
$$ \begin{aligned} B^{\prime} F & =B^{\prime} P+P F \ & =(+v)+(-f) \ & =v-f \ B P & =-u \end{aligned} $$
$$ \therefore \quad \frac{v-f}{-f}=\frac{+v}{-u} $$
or $\quad \frac{-v}{f}+1=\frac{-v}{u}$
$$ \therefore \quad \frac{1}{v}+\frac{1}{u}=\frac{1}{f} $$
This is the mirror formula.
Linear magnification $=\frac{B^{\prime} A^{\prime}}{B A}$
From similar triangte $A{ }^{\prime} B B^{\prime} P^{\prime}$ and $A B P$, we get
$$ \frac{B^{\prime} A^{\prime}}{B A}=\frac{B^{\prime} P}{B P} $$
$\therefore$ Linear magnification
$$ m=\frac{B^{\prime} P}{B P}=\frac{+v}{-u}=-\frac{v}{u} $$
[CBSE Marking Scheme 2018]
Q. 2. (i) Calculate the distance of an object of height $h$ from a concave mirror of radius of curvature $20 \mathrm{~cm}$, so as to obtain a real image of magnification 2. Find the location of image also.
(ii) Using mirror formula, explain why does a convex mirror always produce a virtual image.
R [CBSE Delhi 2017]
Show Answer
Solution:
Ans. (i) Given, $R=-20 \mathrm{~cm}$ and magnification $m=-2$
Focal length of the mirror
$$ \begin{aligned} f & =\frac{R}{2}=-10 \mathrm{~cm} \ \text { Magnification, } m & =-\frac{v}{u} \end{aligned} $$
Using sign convention, for convex mirror, we have From the formula
$$ f>0, u<0 $$
$$ \frac{1}{v}=\frac{1}{f}-\frac{1}{u} $$
$\because f$ is positive and $u$ is negative, $\Rightarrow v$ is always positive, hence image is always virtual
[CBSE Marking Scheme 2017]
