moving-charges-and-magnetism Question 45
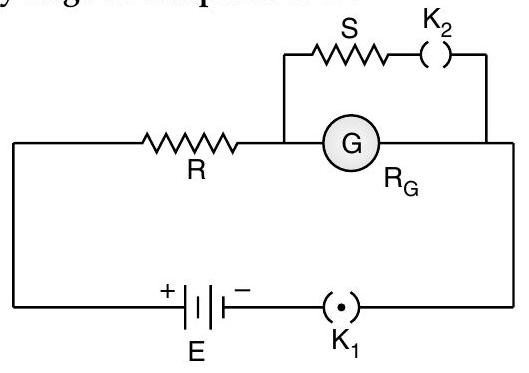
Question: Q. 7. The current flowing in the galvanometer $G$ when the key $K_{2}$ is kept open is $I$. On closing the key $K_{2}$, the current in the galvanometer becomes $I / n$, where $n$ is integer.
Obtain an expression for resistance $R_{g}$ of the galvanometer in terms of $R, \mathrm{~S}$ and $n$. To what form does this expression reduce when the value of $R$ is very large as compared to $S$ ?
U] [CBSE SQP 2014]
Show Answer
Solution:
Ans. With key $K_{2}$ open, the current I in the galvanometer is given by
$$ I=\frac{E}{R+R_{G}} $$
When $K_{2}$ is closed, the equivalent resistance, say $R^{\prime}$, of the parallel combination of $S$ and $R_{G}$ is given by
$$ R^{\prime}=\frac{S R_{G}}{S+R_{G}} $$
The total current, say $I^{\prime}$ drawn from the battery would now be
$$ I^{\prime}=\frac{E}{R+R^{\prime}} $$
This current gets subdivided in the inverse ratio of $S$ and $R_{G}$. Hence the current $I^{\prime \prime}$ through $G$, would now be given by
$$ \begin{gathered} I^{\prime \prime}=\frac{S}{S+R_{G}} \cdot I^{\prime}=\frac{S}{\left(S+R_{G}\right)} \cdot \frac{E}{\left(R+R^{\prime}\right)} \ =\frac{S E}{\left(S+R_{G}\right)\left[R+\frac{S R_{G}}{S+R_{G}}\right]} \end{gathered} $$
$$ \begin{array}{rlrl} & =\frac{S E}{R S+R R_{G}+S R_{G}} \ \text { But } & I^{\prime \prime} & =\frac{I}{n}=\frac{1}{n}\left(\frac{E}{R+R_{G}}\right) \ & \therefore & \frac{E}{n\left(R+R_{G}\right)} & =\frac{S . E}{R S+R R_{G}+S R_{G}} \quad 1 / 2 \ \text { Or } & n R S+n S R_{G} & =R S+R R_{G}+S R_{G} \ \text { Or } & (n-1) R S & =R R_{G}-(n-1) S R_{G} \ \text { Or } & (n-1) R S & =R_{G}[R-(n-1) S] \ & R_{G} & =\frac{(n-1) R S}{R-(n-1) S} \end{array} $$
This is the required expression
When $R»S$, we have
$$ R_{G} \simeq \frac{(n-1) R S}{R}=(n-1) S $$
[CBSE Marking Scheme 2014]
