Solution:

Ans. Working Principle of moving coil galvanometer 1 Necessity of

(i) Radial magnetic field

(ii) Cylindrical soft iron core Expression for current sensitivity

When a coil, carrying current, and free to rotate about a fixed axis, is placed in a uniform magnetic field, it experiences a torque (which is balanced by a restoring torque of suspension).

(i) To have deflection proportional to current/to maximize the deflecting torque acting on the current carrying coil.

(ii) To make magnetic field radial/to increase the strength of magnetic field.

Expression for current sensitivity

$$I_s=\frac{\theta }{I}\text{ or }\frac{NAB}{K}$$

where, $\theta$ is the deflection of the coil

No,

The galvanometer, can only detect currents but cannot measure them as it is not calibrated. The galvanometer coil is likely to be damaged by currents in the $(\mathrm{mA}/\mathrm{A})$ range]

[CBSE Marking Scheme 2017]

Answering Tips

• Learn the working principle of moving coil galvanometer properly.

[A] Q. 5. State the principle of working of a galvanometer. A galvanometer of resistance $G$ is converted into a voltmeter to measure up to $V$ volts by connecting a resistance $R_1$ in series with the coil. If a resistance $R_2$ is connected in series with it, then it can measure up to $\mathrm{V}/\mathbf{2}$ volts. Find the resistance, in terms of $R_1$ and $R_2$, required to be connected to convert it into a voltmeter that can read up to $2\mathrm{V}$. Also find the resistance $G$ of the galvanometer in terms of $R_1$ and $R_2$.

U] [Delhi I, II, III 2015]

Ans. Working principle : A current carrying coil experience torque when placed in a magnetic field which tends to rotate the coil and produces an angular deflection.

$$\text{Multiple tag}$$

$\Rightarrow$ Now, from eqn. (i) $÷$ eqn. (ii),

$$2=\frac{G+R_1}{G+R_2}$$

$\Rightarrow G=R_1-2R_2$

$1/2$

Let $R_3$ be the resistance required for conversion into voltmeter of range $2\mathrm{V}$

$\begin{array}{rlrl}& \therefore & \text{ also }2V=I_g(G+R_3)& V=I(G+R_1)\end{array}$

$\therefore$ From eqn. (iii) $÷$ eqn. (iv),

$$\begin{array}{rlrl}2& =\frac{G+R_3}{G+R_1}{R}_3& =G+2R_1=R_1-2R_2+2R_1& =3R_1-2R_2\end{array}$$

[II Q. 6. (i) Why is the need for magnetic field radial in a moving coil galvanometer ? Explain how it is achieved?

(ii) A galvanometer of resistance ’ $G$ ’ can be converted into a voltmeter of range $(0-V)$ volts by connecting a resistance ’ $R$ ’ in series with it. How much resistance will be required to change its range from 0 to $V/2$ ? U A [O.D. I, II, III 2015]

Ans. (i) Need for a radial magnetic field :

The relation between the current (i) flowing through the galvanometer coil, and the angular deflection $(\varphi )$ of the coil (from its equilibrium position), is

$$\varphi =\left(\frac{NABI\sin \theta }{k}\right)$$

where, $\theta$ is the angle between the magnetic field $\overrightarrow{B}$ and normal to the coil.

Thus I is not directly proportional to $\varphi$. We can ensure this proportionality by having $\theta ={90}^{\circ }$. This is possible only when the magnetic field $\overrightarrow{B}$, is of a radial magnetic field. In such a field, the plane of the rotating coil is always parallel to $\overrightarrow{B}$.

To get a radial magnetic field, the pole pieces of the magnet, are made concave in shape. Also a soft iron cylinder is used as the core.

[Alternatively, Accept if the candidate draws the following diagram to achieve the radial magnetic field.]

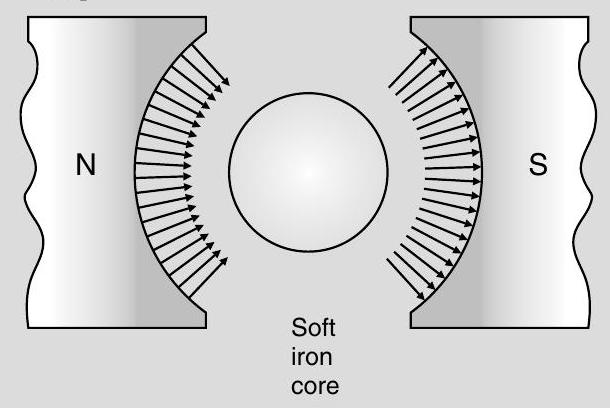
(ii) We have

$$\begin{array}{rlrl}R& =(\frac{V}{I_m}-G)I_m& =\frac{V}{R+G}{I}_m& =\frac{\left(\frac{V}{2}\right)}{R^{\prime }+G}\end{array}$$

We must also have

where, $R^{\prime }=$ Resistance required to change the range from 0 to $\mathrm{V}/2$,

$$\begin{array}{rlrlllll}{I}_m& =I_m{}^{\prime }& \therefore & \frac{V}{R+G}& =\frac{V}{2(R^{\prime }+G)}& \therefore & R^{\prime }& =\frac{R-G}{2}\end{array}$$

[CBSE Marking Scheme 2015]