moving-charges-and-magnetism Question 41
Question: Q. 1. (i) What is the importance of a radial magnetic field and how is it produced?
(ii) Why is it that while using a moving coil galvanometer as a voltmeter a high resistance in series is required whereas in an ammeter a shunt is used? U[ [Delhi Comptt. I, II, III 2013]
Show Answer
Solution:
Ans. (i) Importance and production of radial magnetic field : In a radial magnetic field, magnetic torque remains maximum everywhere.
(ii) Voltmeter : A high resistance in series is required when moving coil galvanometer is used as voltmeter to make sure that a low current should travel through voltmeter without changing the potential difference then needs to be measured.
[AI Q. 2. Explain giving reasons, the basic difference in converting a galvanometer into (i) a voltmeter and (ii) an ammeter.
U [O.D. I, II, III 2012]
Ans. (i) Try yourself, Similar to Q. 1, (ii) Short Answer Type Questions-I
(AI Q. 3. A square loop of side
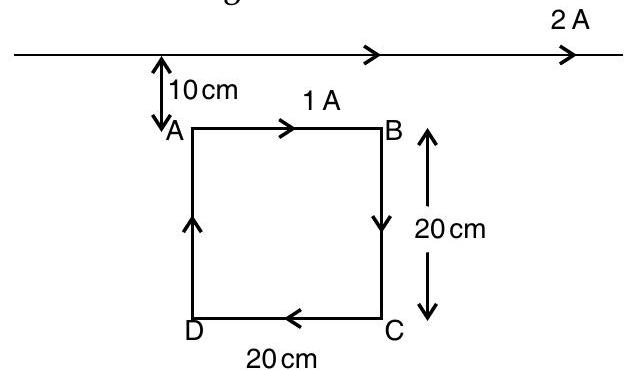
Calculate the magnitude and direction of the net force exerted on the loop due to the current carrying conductor.
A [O.D. I, II, III 2015] OR
A square shaped plane coil of area
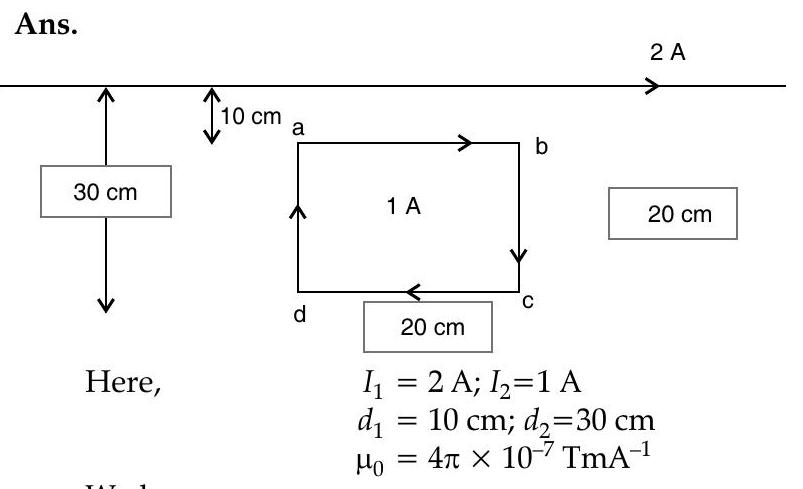
We have
This net force is directed towards the infinitely long straight wire.
Net force on sides
The force is directed towards the infinitely long straight wire.






