Solution:

Ans. (i) A current carrying surface with small line elements of length $d l$ where tangential components. of magnetic field and sum of elements B.dl in an integral form be expressed as :

$$ \oint \vec{B} \cdot \overrightarrow{d l}=\mu_{0} i $$

This form is known as Ampere’s circuital law. 1/2

$1 / 2$

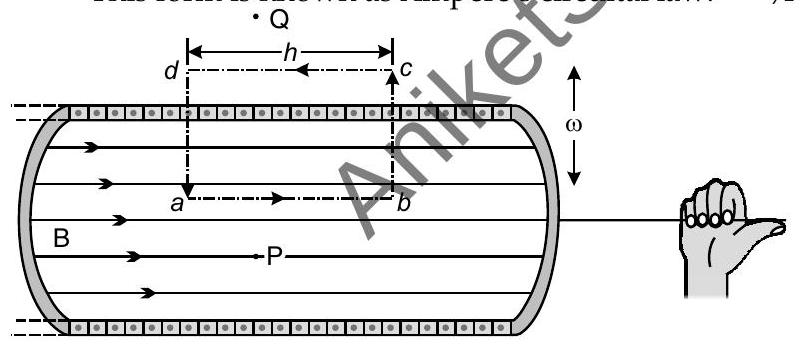
Let ’ $n$ ’ be the number of turns per unit length. Then total number of turns in the length ’ $h$ ’ is $n h$.

Hence, total enclosed current $=n h I$ Using Ampere’s circuital law

$$ \oint \vec{B} \cdot \overrightarrow{d l}=\mu_{0} n h I $$

$$ B h=\mu_{0} n h I $$

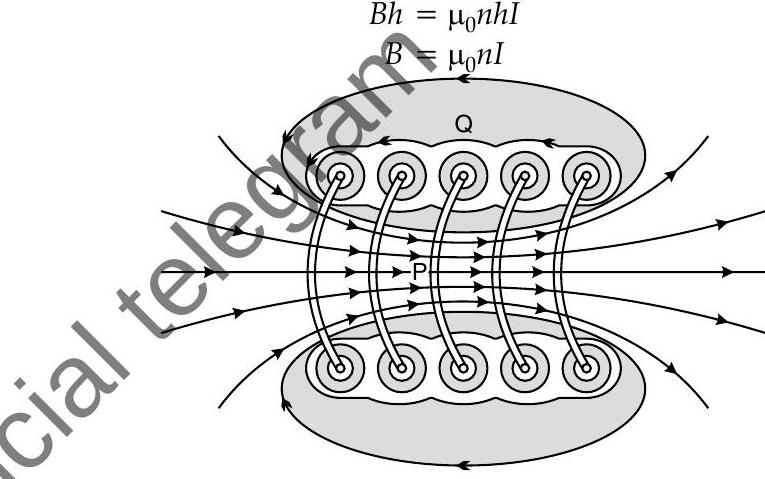
(ii)

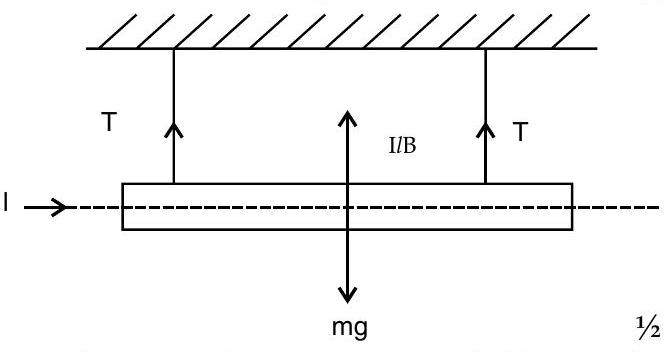
As per the given figure, magnetic field must be vertically inwards, to make tension zero, (If a student shows current in opposite direction the magnetic field should be set up vertically upwards).

$$ I l B=m g $$

For tension to be zero,

$$ \begin{aligned} B=\frac{m g}{\mathrm{I} l} & =\frac{60 \times 10^{-3} \times 9.8}{5.0 \times 0.45} \mathrm{~T} \quad 1 / 2 \ & =0.26 \mathrm{~T} \end{aligned} $$

TOPIC-3

Torque and Galvanometer

Revision Notes

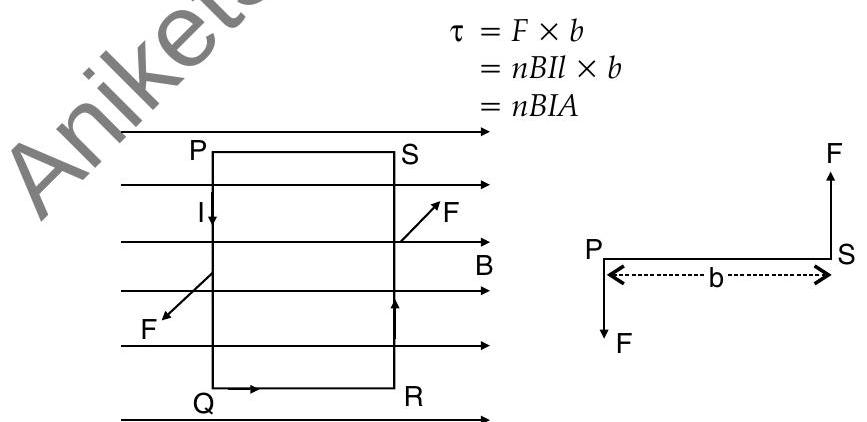
Torque experienced by a current loop in uniform magnetic field

In a rectangular loop of length $l$, breadth $b$ with current $I$ flowing through it in a uniform magnetic field of induction $B$ where angle $\theta$ is between the normal and in direction of magnetic field, then the torque experienced will be :

where, $n=$ number of turns in the coil $\therefore n I A=m$

Further,

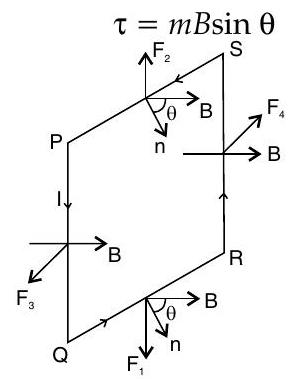
Torque will be maximum when the coil is parallel to magnetic field and will be zero when coil is perpendicular to magnetic field.

In vector notation, torque $\vec{\tau}$ experienced will be $\vec{\tau}=\vec{m} \times \vec{B}$

Moving coil galvanometer

It is an instrument used for detection and measurement of small electric currents

In this, when a current carrying coil is suspended in uniform magnetic field, it experiences a torque which rotates the coil.

The force experienced by each side of the galvanometer will be $F=B I l$ which are opposite in direction.

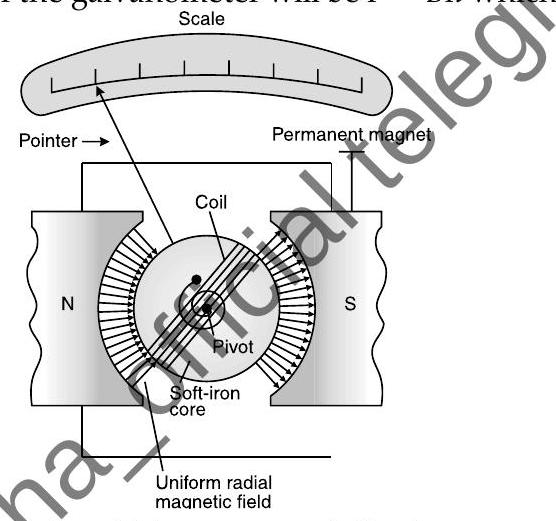
Opposite and equal forces form the cquple which generates deflecting torque on the coil having number of turns $n$ is given as :

In moving coil galvanometer, current in the coil will be directly proportional to the angle of the deflection of the coil, $\quad I \propto \theta$ i.e., where, $\theta$ is the angle of deflection.

Current sensitivity of galvanometer

Current sensitivity of galvanometer is the deflection produced when unit current passes through the galvanometer. A galvanometer is said to be sensitive if it produces large deflection for a small current.

$$ \begin{aligned} \mathrm{I} & =\frac{C}{n B A} \theta \ \frac{\theta}{I} & =\frac{n B A}{C} \end{aligned} $$

Current Sensitivity,

Voltage sensitivity of galvanometer is the deflection per unit voltage given as

Voltage Sensitivity, $\quad \frac{\theta}{V}=\frac{\theta}{I G}=\frac{n B A}{C G}$ where, $G=$ galvanometer resistance, $C=$ torsional constant.

Increase in sensitivity of moving coil galvanometer depends on :

(i) number of turns $n$ (ii) magnetic field $B$ (iii) area of coil $A$ and (iv) torsional constant.

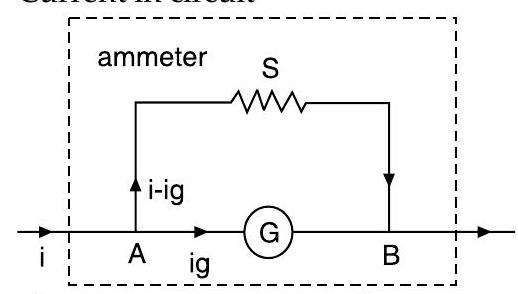
Conversion of galvanometer into ammeter

Galvanometer can be converted into ammeter by connecting a low resistance known as shunt in parallel with the galvanometer coil.

If $I_{g}$ being the maximum current with full scale deflection that passes through galvanometer, then current through shunt resistance will be

$$ i_{s}=\left(i-i_{g}\right) $$

where, $G=$ Galvanometer resistance, $S=$ Shunt resistance and $i=$ Current in circuit

D Now effective resistance of ammeter will be :

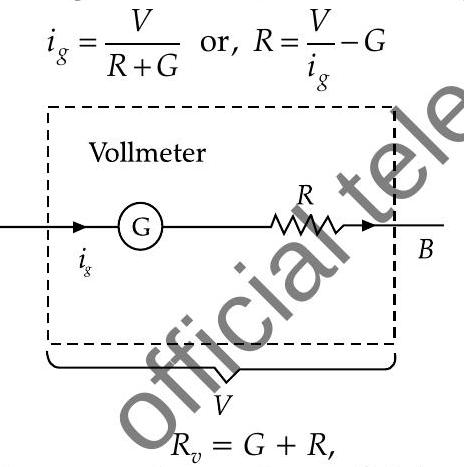
Conversion of galvanometer into voltmeter

$$ \begin{aligned} \frac{1}{R_{a}} & =\frac{1}{G}+\frac{1}{S} \ R_{a} & =\frac{G S}{G+S} \end{aligned} $$

Voltmeter measures the potential difference between the two ends of a current carrying conductor.

Galvanometer can be converted to voltmeter by connecting high resistance in series with galvanometer coil.

As resistance $R$ is connected in series with galvanometer, current through the galvanometer will be,

• Effective resistance of voltmeter is

where, $R_{v}$ is very large making the voltmeter to onnect in parallel since it can draw less current from the circuit.

Key Formulae

Force between two parallel wires $\mathrm{F}=\frac{\mu_{0}}{4 \pi} \times \frac{2 i_{1} i_{2}}{a} \times l$

• Force between two moving charge particle $F_{m}=\frac{\mu_{0}}{4 \pi} \times \frac{q_{1} q_{2} v_{1} v_{2}}{r^{2}}$

$>\tau_{\max }=N B i A$

$>$ Current Sensitivity $=\frac{\theta}{I}=\frac{n A B}{C}$

$>$ Voltage Sensitivity $=\frac{\theta}{V}=\frac{n A B}{C G}$

f. Very Short Answer Type Questions

[II Q. 1. A multi-range voltmeter can be constructed by using the galvanometer circuit as shown. We want to construct a voltmeter that can measure $2 \mathrm{~V}, 20 \mathrm{~V}$ and $200 \mathrm{~V}$ using a galvanometer of resistance $10 \Omega$ and that produces maximum deflection for current of $1 \mathrm{~mA}$. Find $R_{1}, R_{2}$ and $R_{3}$ that have to be used.

$$ \begin{aligned} & \text { Ans. } i_{G}\left(G+R_{1}\right)=2, R_{1}=1.99 \mathrm{k} \Omega \approx 2 \mathrm{k} \Omega \ & \begin{array}{r} i_{G}\left(G+R_{1}+R_{2}\right)=20, R_{2}=18 \mathrm{k} \Omega \quad \text { for } 2 \mathrm{~V} \text { range } \ \text { for } 20 \mathrm{~V} \text { range } \end{array} \ & i_{G}\left(G+R_{1}+R_{2}+R_{3}\right)=200, R_{3}=180 \mathrm{k} \Omega \ & \text { for } 200 \mathrm{~V} \text { range } 1 \ & \text { [CBSE Marking Scheme, } 2017] \end{aligned} $$

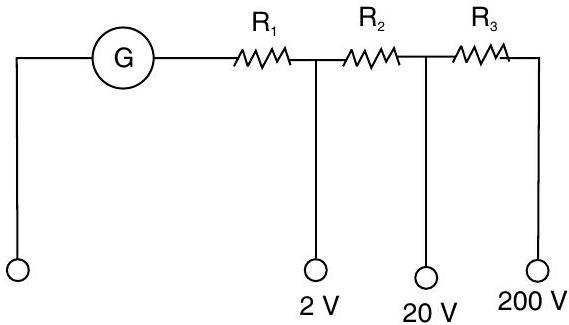
Detailed Answer :

From the question,

$$ \begin{aligned} & G=10 \Omega, \ & i_{G}=1 \mathrm{~mA}=10^{-3} \mathrm{~A} \end{aligned} $$

For $2 \mathrm{~V}$ range,

$$ i_{G}\left(G+R_{1}\right)=2, \mathrm{R}_{1}=1.99 \mathrm{k} \Omega \approx 2 \mathrm{k} \Omega $$

For $20 \mathrm{~V}$ range,

$$ \begin{aligned} i_{G}\left(G+R_{1}+R_{2}\right) & =20 \ R_{2} & =18 \mathrm{k} \Omega \end{aligned} $$

For $200 \mathrm{~V}$ range,

$i_{G}\left(G+R_{1}+R_{2}+R_{3}\right)=200$

$$ R_{3}=180 \mathrm{k} \Omega $$

Answering Tips

• Sometimes students commit errors while substituting the values.