moving-charges-and-magnetism Question 33
Question: Q. 8. (a) Define SI unit of current in terms of the force between two parallel current carrying conductors.
(b) Two long straight parallel conductors carrying steady currents $I_{a}$ and $I_{b}$ along the same direction are separated by a distance $d$. How does one explain the force of attraction between them ? If a third conductor carrying a current $I_{c}$ in the opposite direction is placed just in the middle of these conductors, find the resultant force acting on the third conductor. B&U[CBSE Comptt. I, II, III 2018]
Sol. (a) Definition of SI unit of current 1 (b) Explanation of the force of attraction $1 / 2$ Finding the resultant force acting on the third conductor
(a) One ampere is the value of that steady current which, when maintained in each of the two very long, straight, parallel conductors of negligible crosssection, and placed one metre apart in vacuum, would produce on each of these conductors a force equal to $2 \times 10^{-7}$ newton per metre of length. $\mathbf{1}$
(b) The wire (b) experiences a force due to the magnetic field caused by the current flowing in wire (a).
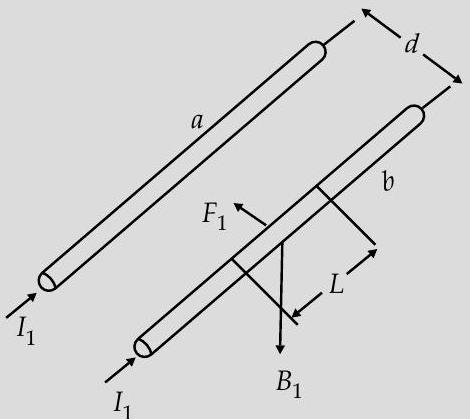
The magnetic field at any point on the wire (b) due to the current in wire (a) is perpendicular to the plane of two wires and pointing inwards and hence force on it will be towards wire (a). Similarly force on wire (a) will be towards wire (b). Hence two wires carrying currents in same direction attract each other.
Force on wire (3) due to wire (1)
$=\frac{\mu_{0} I_{a} I_{c}}{2 \pi\left(\frac{d}{2}\right)}$ towards right
Force on wire 3 due to wire 2
$\left(\frac{\mu_{0} I_{b} I_{c}}{2 \pi\left(\frac{d}{2}\right)}\right)$ towards left
Net force on wire 3
$=\frac{\mu_{0} I_{c}}{\pi d}\left[I_{a}-I_{b}\right]$ towards right
Also accept
$=\frac{\mu_{0} I_{c}}{\pi d}\left[I_{b}-I_{a}\right]$ towards left
Note: please do not deduct last $1 / 2$ mark if the student does not write the direction of force.
[CBSE Marking Scheme 2018]
Q. 9. A horizontal wire $A B$ of length $l$ and mass $m$ carries a steady current $I_{1}$, free to move in vertical plane is in equilibrium at a height of $h$ over another parallel long wire $C D$ carrying a steady current $I_{2}$, which is fixed in a horizontal plane. Derive an expression for force acting per unit length on the wire $A B$ and write the conditions for which wire $A B$ is in equilibrium ?
U] [CBSE SQP 2017-18]
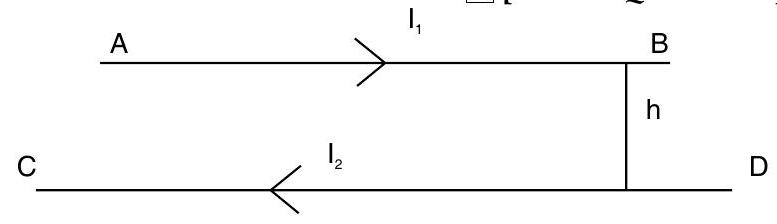
Show Answer
Solution:
Ans. $A B$ and $C D$ are two parallel wires, so when the current flows in similar direction, both the wires, will attract and when the current in one wire flows in opposite direction, they repel.
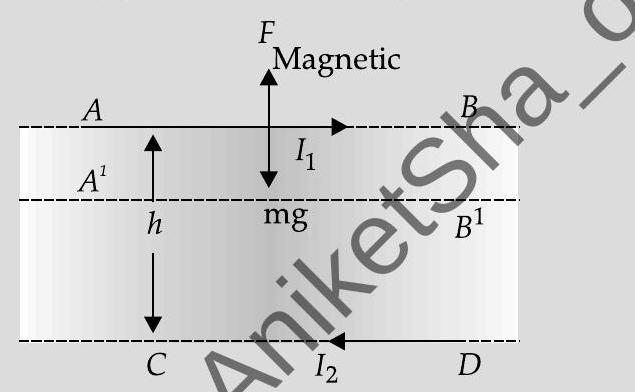
Now consider the above diagram, if wire $A B$ is steady, then weight per unit length will be equal to force per unit length, so
Weight per unit length $=\frac{m g}{l}$
Further, the restoring force/length $=\frac{\mu_{0}}{4 \pi} \times \frac{2 I_{1} I_{2}}{h} \quad \mathbf{1}$ At equilibrium, magnetic force per unit length will be mass per unit length $\times \mathrm{g}$, so $F=\frac{m}{l} g=\frac{\mu_{0} I_{1} I_{2}}{2 \pi h}$
[CBSE Marking Scheme 2017] 1
