Solution:

Ans. Formula for magnetic field of toroid 1

Calculation of magnetic field $1\frac{1}{2}$

Effect of change of core

$1/2$ $1/2$

$B={\mu }_r{\mu }_{0}nI$

$$=(800\times 4\pi \times {10}^{-7})\times \left(\frac{4000}{2\pi \times 20\times {10}^{-2}}\right)\times 3$$

$$=9.6\mathrm{T}$$

Since Bismuth is diamagnetic, its ${\mu }_r<1$

$\therefore$ The magnetic field in the core will get very much reduced.

[CBSE Marking Scheme 2017]

Detailed Answer :

Given :

Mean radius of toroidal solenoid $=20\mathrm{cm}$

Number of turns of wire wound $=4000$

Relative permeability of ferromagnetic core $=800$

Current passing through the coil $=3\mathrm{A}$

Magnetic field in a toroid coil :

$$\begin{array}{}\text{(1)}& B=\frac{{\mu }_{0}NI}{2\pi r}\end{array}$$

Now,

$$B=\frac{800\times 4\pi \times {10}^{-7}\times 4000\times 3}{2\pi \times 20\times {10}^{-2}}1/2$$

$$\begin{array}{}\text{(1)}& B=9.6\mathrm{T}\end{array}$$

It is observed that as Bismuth is diamagnetic substance with relative permeability less than 1 , it will have a tendency to move away from the stronger to weak part of external magnetic field making the core field less as compared to empty core field.

[AI Q. 4. (i) State Ampere’s circuital law, expressing it in the integral form.

(ii) Two long co-axial insulated solenoids, $S_1$ and $S_2$ of equal lengths are wound one over the other as shown in the figure. A steady current " $I$ " flows through the inner solenoid $S_1$ to the other end $B$, which is connected to the other solenoid $S_2$ through which the same current " $I$ " flows in the opposite direction so as to come out at end $A$. If $n_1$ and $n_2$ are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.

U [Delhi I, II, III 2014]

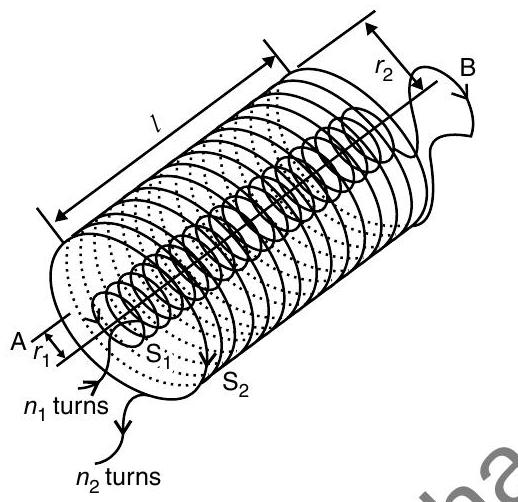
Ans. (i) Ampere’s circuital law : The lineintegral of the magnetic field around a closed path is ${\mu }_0$ times of total current enclosed by the path.

$$\oint \overrightarrow{B}\cdot \overrightarrow{dl}\leftrightharpoons {\mu }_{0}I$$

(Award 1 mark if the student just writes the integral form of Ampere’s circuital law)

(ii) (a)

$$B={\mu }_{0}nI$$

Magnitude of net magnetic field inside the combined system on the axis,

$$\begin{array}{rlr}& B=B_1-B_2\Rightarrow & B={\mu }_0(n_1-n_2)I\end{array}$$

$$\text{ Also accept if the student writes }B={\mu }_0(n_2-n_1)I$$

(b) Outside the combined system, the net magnetic field is zero.

[CBSE Marking Scheme 2014]