moving-charges-and-magnetism Question 16
Question: Q. 9. Consider the motion of a charged particle of mass $m$ and charge $q$ moving with velocity $\vec{v}$ in a magnetic field $\vec{B}$.
(i) If $\vec{v}$ is perpendicular to $\vec{B}$, show that it describes a circular path having angular frequency
$\rightarrow \omega=q B / m$.
(ii) If the velocity $\vec{v}$ has a component parallel to the magnetic field $\vec{B}$, trace the path described by the particle. Justify your answer.
U] [Delhi Comptt. I, II, III 2014]
Show Answer
Solution:
Ans. (i) Force acting on the charged particle, moving with a velocity $\vec{v}$, in a magnetic field $\vec{B}$ :
$$ \vec{F}=q(\vec{v} \times \vec{B}) $$
As, $\vec{v} \perp \vec{B}, \quad \mathrm{~F}=q v B$
Since, $\vec{F} \perp \vec{v}$, it acts as a centripetal force and makes the particle move in a circular path in the plane, perpendicular to the magnetic field.
$\therefore \quad q v B=\frac{m v^{2}}{r}$
$\therefore \quad r=\frac{m v}{q B}$ or $\frac{v}{r}=\frac{q B}{m}$
Now
$$ \omega=\frac{v}{r} $$
$$ \omega=\frac{q B}{m} $$
(ii)
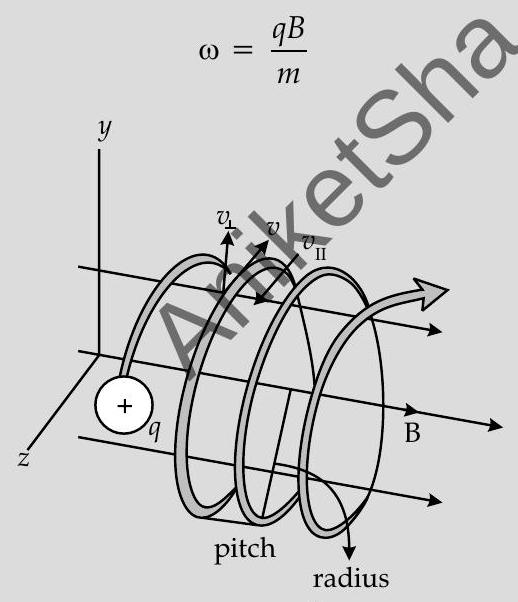
The component of velocity $\vec{v}$ parallel to magnetic field, will make the particle move along the field.
The perpendicular component of velocity $\vec{v}$ will cause the particle to move along a circular path in the plane perpendicular to the magnetic field. Hence, the particle will follow a helical path, as shown.
[CBSE Marking Scheme, 2014] 1
