moving-charges-and-magnetism Question 11
Question: Q. 2. A particle of mass 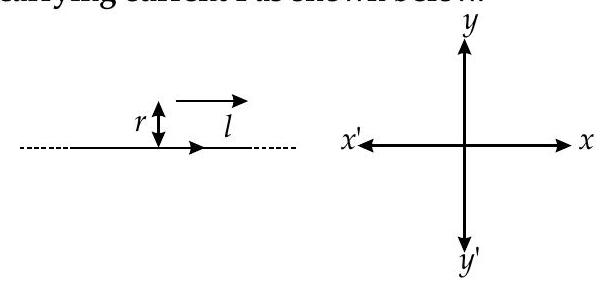
Find magnitude and direction of electric field required so that the particle goes undeflected.
R&U [CBSE SQP 2018]
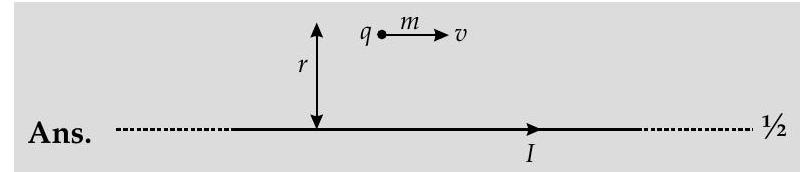
For the charged particle to move undeflected
Net force,
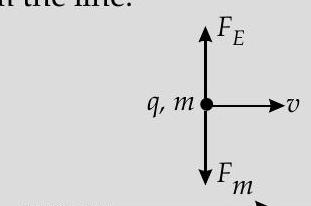
$$ \begin{align*} \vec{F} & =\vec{F}{E}+\overrightarrow{F{m}}=\overrightarrow{0} \ \overrightarrow{F_{E}} & =-\overrightarrow{F_{m}} \tag{1} \end{align*} $$
$$ \begin{align*} \left|\vec{F}{E}\right| & =\left|\vec{F}{m}\right| \tag{2}\ q E & =B q v \sin 90^{\circ}=B q v \ E & =v B \ B & =\frac{\mu_{0} I}{2 \pi r} \tag{4} \end{align*} $$
Using (4) and (3)
Magnetic force
[CBSE Marking Scheme 2018]
AI Q. 3. (a) State Biot-Savart’s law and express it in the vector form.
(b) Using Biot-Savart’s law, obtain the expression for the magnetic field due to a circular coil of radius
R&U [CBSE Comptt. I, II, III 2018]
$\begin{array}{cc}\text {
Show Answer
Solution:
Ans. (a) Statement of Biot-Savart law } & 1 / 2 \ \text { Its vector form } & 1 / 2\end{array}$
(b) Obtaining the required expression
(a) According to Biot Savart law :
The magnitude of magnetic field
(i) proportional to current
(ii) inversely proportional to the square of the distance
Its direction is perpendicular to the plane containing
In vector notation,
(b)
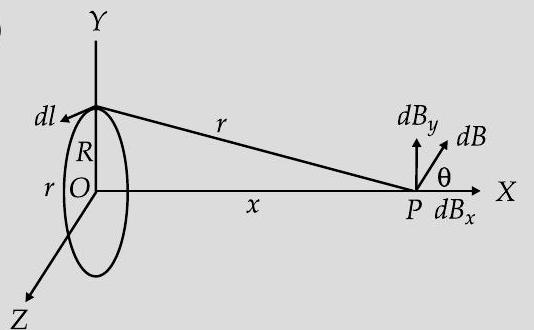
We have,
We need to add only the components of
Hence,
[CBSE Marking Scheme 2018]






