magnetism-and-matter Question 7
Question: Q. 1. An electron of mass $m_{e}$ revolves around a nucleus of charge $+Z e$. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as $\vec{\mu}=-\frac{e}{2 m_{e}} \vec{L}$, where $\vec{L}$ is the orbital angular momentum of the electron. Give the significance of negative sign.
U] [Delhi II 2017, 2014]
Show Answer
Solution:
Ans. (i) Behaviour of revolving electron as a tiny magnetic dipole.
(ii) Proof of the relation $\vec{\mu}=-\frac{e}{2 m_{e}} \vec{L}$
(iii) Significance of negative sign Electron, in circular motion around the nucleus constitutes a current loop which behaves like a magnetic dipole.
Current associated with the revolving electron : $\mathbf{4}$
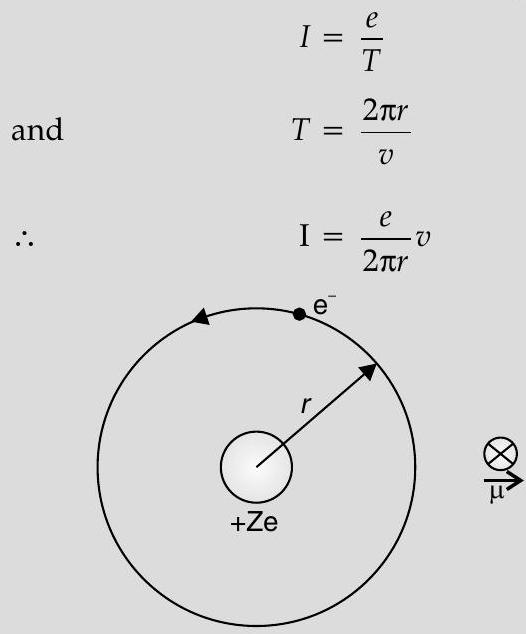
Magnetic moment of the loop,
$$ \begin{aligned} \mu & =I A=\frac{e v}{2 \pi r} \pi r^{2} \ & =\frac{e v r}{2}=\frac{e \cdot m_{e} v r}{2 m_{e}} \end{aligned} $$
Orbital angular momentum of the electron,
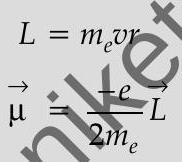
-ve sign signifies that the angular momentum of the revolving electron is opposite in direction to the magnetic moment associated with it.
[CBSE Marking Scheme 2017]
