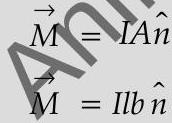magnetism-and-matter Question 5
Question: Q. 4. A coil of ’ $N$ ’ turns and radius ’ $R$ ’ carries a current ’ $I$ ‘. It is unwound and rewound to make a square coil of side ’ $a$ ’ having same number of turns $(N)$. Keeping the current ’ $I$ ’ same, find the ratio of the magnetic moments of the square coil and the circular coil. C [Delhi Comptt. I, II, III 2013]
Show Answer
Solution:
Ans.
$$ \begin{aligned} A_{1} & =\pi R^{2} \ m_{1} & =N I A_{1} \ A_{2} & =a^{2} \ m_{2} & =N I A_{2} \ \frac{m_{1}}{m_{2}} & =\frac{N I A_{1}}{N I A_{2}} \ & =\frac{\pi R^{2}}{a^{2}} \ \frac{m_{1}}{m_{2}} & =\frac{22}{7}\left(\frac{R}{a}\right)^{2} \end{aligned} $$
[Square coil] [AI Q. 1. A rectangular coil of sides ’ $l$ ’ and ’ $b$ ’ carrying a current $I$ is subjected to a uniform magnetic field $\vec{B}$, acting perpendicular to its plane. Obtain the expression for the torque acting on it.
U] [Delhi Comptt. I, II, III 2014]
Ans. Equivalent magnetic moment of the coil,
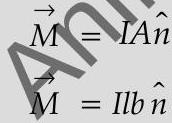
( $\hat{n}=$ unit vector $\perp$ to the plane of the coil)
$$ \begin{align*} \text { Torque } & =\vec{M} \times \vec{B} \ & =I l b \hat{n} \times \vec{B} \ & =0 \end{align*} $$
(as $\hat{n}$ and $\vec{B}$ are parallel or antiparallel to each other)
[CBSE Marking Scheme 2014]
