Solution:

Ans. (a) The magnetic potential energy $U_{m}$ is given by

$$ U_{m}=\int \tau(\theta) d \theta $$

[AI Q. 3. (a) A small compass needle of magnetic moment ’ $m$ ’ is free to turn about an axis perpendicular to the direction of uniform magnetic field ’ $B$ ‘. The moment of inertia of the needle about the axis is ’ $I$ ‘. The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.

(b) A compass needle, free to turn in a vertical plane orient itself with its axis vertical at a certain place on the earth. Find out the values of (i) horizontal component of earth’s magnetic field and (ii) angle of dip at that place.

U [Delhi 2013]

Ans. (a) Let magnetic needle is suspended in the uniform external magnetic field $B$ and making angle $\theta$ with it and is slightly disturbed to oscillate in this field.

As Magnetic moment $\vec{M}$ is directed along the axis of needle, torque $\tau$ on the needle is

$$ \begin{aligned} \vec{\tau} & =\vec{M} \times \vec{B} \ & =M B \sin \theta \end{aligned} $$

We also know that

$$ \tau=I \alpha $$

Where $I$ is moment of inertia of needle and $\alpha$ angular acceleration

Angular acceleration,

Hence,

$$ \begin{aligned} \alpha & =\frac{d^{2} \theta}{d t^{2}} \ \tau & =I \frac{d^{2} \theta}{d t^{2}}=-M B \sin \theta \end{aligned} $$

(-ve sign implies that this torque is acting as restoring torque).

Now if $\theta$ is small then $\sin \theta=\theta$

$$ \begin{aligned} & \text { So, } \ & I \frac{d^{2} \theta}{d t^{2}}=-M B \theta \ & \text { Or } \ & \frac{d^{2} \theta}{d t^{2}}=\left(\frac{-M B}{I}\right) \theta \end{aligned} $$

This derived equation is similar to equation of simple harmonic motion,

$$ \frac{d^{2} \theta}{d t^{2}}=-\omega^{2} \theta $$

where,

$$ \omega^{2}=\frac{M B}{I} $$

Hence, proved that it executes simple harmonic motion.

We know that

$$ \omega=\frac{2 \pi}{T} $$

where, $T$ is period of oscillation.

Putting the value of $\omega=\sqrt{\frac{M B}{I}}$

$$ \begin{align*} \sqrt{\frac{M B}{I}} & =\frac{2 \pi}{T} \ \mathrm{~T} & =2 \pi \sqrt{\frac{I}{M B}} \tag{1} \end{align*} $$

(b) Horizontal component of earth’s magnetic field $H$ $=B \cos \theta$

If needle orients itself with its axis vertical at a certain place on the earth then $\theta=90^{\circ}$

So, $H=0$

Angle of dip $=$ The angle that magnetic field make with horizontal line at that point. For a compass needle align vertical at a certain place means is $90^{\circ}$. 1

TOPIC-2
Magnetic field of a Solenoid, 2 arth’s Magnetism & Magnetic properties of Materials

Revision Notes

Bar magnet as an equivalent solenoid

• If a solenoid of length $2 l$, radius $a$ with current $I$ having $n$ number of turns per unit length, then the magnetic moment of solenoid,

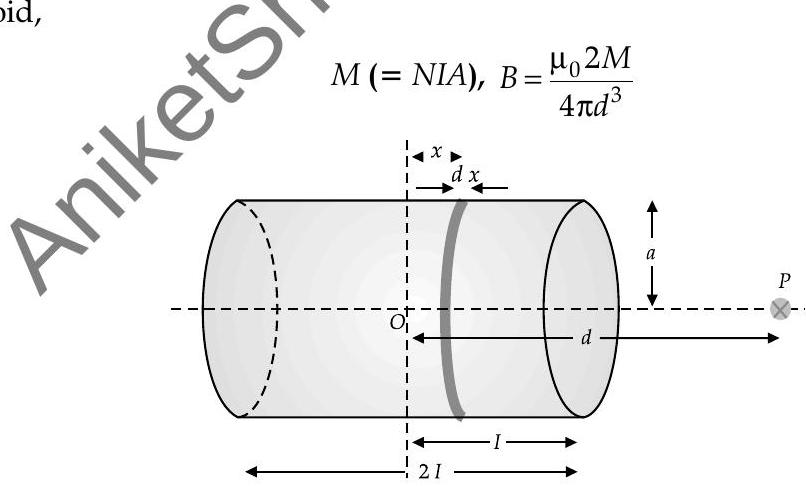
Magnetic moment of a bar magnet is equal to magnetic moment of an equivalent solenoid that produces same magnetic field.

Gauss’s Law for Magnetic Fields

• Gauss’ Law for magnetism applies to the magnetic flux through a closed surface.

Shows that no magnetic monopoles exist and total flux through closed surface will be zero.

The Gauss’s law for magnetic fields in integral form is given by

$$ \phi=\int B \cdot d A=0 $$

Earth’s Magnetism

Darth shows magnetic properties. This is evident from the following facts

• A freely suspended needle stays in north south direction.
• Availability of neutral points. At neutral points, magnetic field due to suspended magnet is equal and opposite to the horizontal component of earth’s magnetic field.

The source of Earth’s magnetism is still unknown, though certain theories have good scientific justifications like ions revolving with earth.

Characteristics of Earth’s Magnetism

Earth’s south pole and north pole are defined by Sun’s direction. These are known as geographical north and south poles. Magnetic north and south poles are the points where the magnetic needle becomes perpendicular to earth’s surface. Hence, there are two system of directions.

Due to two system of directions, we can draw two meridians. (Plane joining geographic North and South pole is geographic meridian and plane joining magnetic North and South pole is magnetic meridian)

Elements of earth’s magnetic field

Angle of Declination : At any place on earth, the acute angle between magnetic meridian and the geographical meridian is called the angle of declination.

• Angle of Dip : The angle of dip at any place is the angle between earth’s magnetic field intensity $B$ with horizontal in the magnetic meridian at that place.

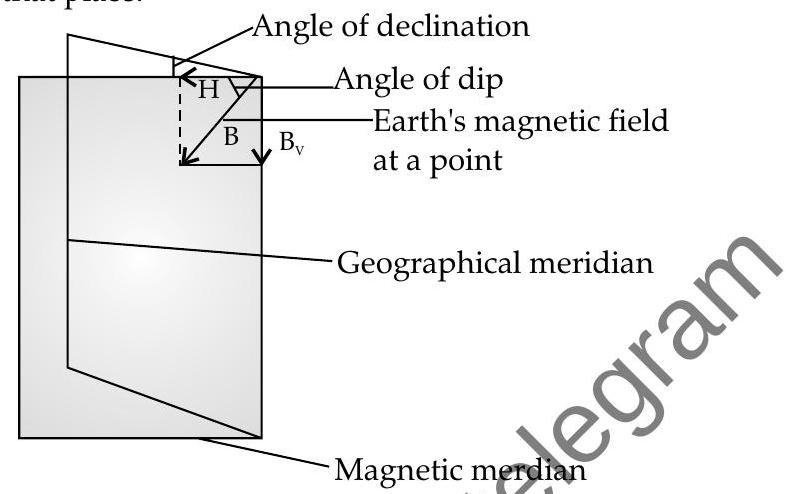
Horizontal Component of Earth’s Magnetic field : The horizontal component of Earth’s magnetic field $\mathrm{H}$ is in the horizontal direction in the magnetic meridian.

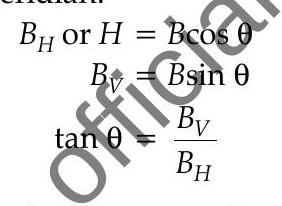
Where $\theta$ is angle of Dip,

We find the earth’s magnetic field $B$ at any place by measuring its horizontal component. Hence,

$$ B=\frac{H}{\cos \theta} \text { and } B_{V}=H \tan \theta $$

There is variation in magnetic field between place to place depending upon angle of Dip, angle of declination and magnetic field horizontal component of earth, Hence, these are known as elements of Earth’s magnetic field.

Magnetic elements : para-, dia- and ferro-magnetic substances

Ferromagnetic Substances

• The substances, which are placed in external magnetising field, get magnetised very strongly in the direction of the magnetising field are called ferromagnetic substances. Examples of ferromagnetic substances : iron, nickel, cobalt and certain alloys such as alnico.

Ferromagnetism is not found in liquids and gases.

Curie Point : The ferromagnetism depends on the temperature. If we raise temperature of the ferromagnetic substance, the domains may disintegrate and the substance turns paramagnetic. The temperature at which this happens is called Curie point. Thus, the Curie point is the temperature above which the ferromagnetic substance looses ferromagnetism and turns into a paramagnetic substance.

• Ferromagnetic substances are strongly magnetised and their induced dipole moment $M$ is in the direction of the magnetising field $H$.

For ferromagnetic substances, $\quad \mu_{r}»1$

$>\chi_{m}$ of ferromagnetic substance is positive and large.

$\mathrm{B}$ (magnetic induction) inside the ferromagnetic substances is much larger than that in vacuum. $B$ for ferromagnetic substances is much larger than that for paramagnetic substances.

They move from the weaker regions of the magnetic field to the stronger regions.

They are strongly attracted by a bar magnet.

If a bar magnet of ferromagnetic material is freely suspended between the pole pieces of a magnet, it aligns itself along the magnetic field.

The liquids do not exhibit ferromagnetism. However, if a finely powdered ferromagnetic substance is placed in the watch glass kept on the pole pieces of a magnet, it elevates from the middle when pole pieces are closed together which suffers a depression in the middle when the pole pieces are far apart.

Area under a $B$ - $H$ curve represents power loss per unit volume per cycle.

Diamagnetic Substances :

The substances, which when placed in external magnetising field, get magnetised feebly in a direction opposite to the magnetising field are called diamagnetic substances.

Examples of diamagnetic substances : Copper, silver, gold, bismuth, zinc, lead, glass, marble, sodium chloride, water and gases such as helium, argon, etc.

Diamagnetic substances are feebly magnetised and their induced magnetic dipole moment is directed opposite to the magnetising field $\mathrm{H}$.

For diamagnetic substances, $\quad 0 \leq \mu_{r}<1$.

$\chi_{m}$ of diamagnetic substances is negative and small, $-1 \leq \chi_{m}<0$.

$B$ (magnetic induction field) inside the diamagnetic materials is less than that in vacuum, because,

Because $\chi_{m}$ is negative, therefore $B$ is less than $H$

$$ \begin{aligned} & B=\mu_{0}(H+M) \ & B=\mu_{0}\left(H+\chi_{m} H\right)=\mu_{0}\left(1+\chi_{m}\right) H \end{aligned} $$

$$ B_{0}=\mu_{0} H $$

They move from the stronger regions of magnetising field to the weaker regions.

They are repelled by a bar magnet.

• If a bar of diamagnetic material is suspended between the pole pieces of a magnet, it aligns itself perpendicular to the magnetic field of the magnet.

Diamagnetic substances do not obey the Curie’s law.

Diamagnetic properties are independent of the temperature. Paramagnetic Substances :

The substances which when placed in an external magnetising field, get weakly magnetised in the direction of magnetic field are called paramagnetic substances.

Examples of paramagnetic substances : Aluminium, antiprony, platinum, manganese, sodium, chromium, liquid oxygen, etc.

Paramagnetic substances are feebly magnetised and their induced magnetic dipole moment $M$ is in the direction of the magnetising field $H$.

For paramagnetic substance $\mu_{r}>1$ but small, $1<\mu_{r}<1+\varepsilon$.

$>\chi_{m}$ of paramagnetic substances is positive but small, $0<\chi_{m}<\varepsilon$.

$B$ (magnetic induction field) inside the paramagnetic materials is slightly more than that in vacuum.

They move from the weaker regions of magnetic field to the stronger regions.

They are attracted by a bar magn

If a bar magnet of paramagnetic material is suspended between the pole pieces of the magnet it aligns itself parallel to the magnetising field of the magnet.

The paramagnetism depends on the temperature. As the temperature increases, magnetisation tends to decrease.

• Paramagnetic substances obey the Curie’s law, which states that the magnetic susceptibility is inversely proportional to the temperature in kelvin,

i.e.,

$$ \chi_{m} \propto \frac{\mathrm{I}}{\mathrm{T}} $$

Dip is zero at the equator and $90^{\circ}$ at the magnetic poles.

Paramagnetism and ferromagnetism are associated with the intrinsic magnetic moment of spinning of electrons.

In ferromagnetism, the magnetic effect is enhanced due to the formation of domains.

Magnetic induction $B$ and magnetic intensity $H$ are related as

$$ B=\mu H . $$

• Magnetic induction is expressed in Tesla (S.I.) and Gauss (C.G.S. system).

Magnetic intensity in vacuum is expressed in Oersted (C.G.S. system) and $\mathrm{Am}^{-1}$ (SI unit).

Diamagnetism originates from the magnetic moment associated with the orbital motion of electrons.

• Curie’s Law in Magnetism : The intensity of magnetisation I of a paramagnetic material is directly proportional to the strength of the external magnetic field $\mathrm{H}$, called the magnetising field and is inversely proportional to absolute temperature of the material.

$$ \begin{array}{ll} & \mathrm{I} \propto \frac{H}{T} \ \therefore \quad & \mathrm{I}=\frac{C H}{T} \end{array} $$

$$ \begin{aligned} & \Rightarrow \quad \frac{I}{H}=\frac{C}{T} \ & \text { or } \ & \chi=\frac{C}{T} \end{aligned} $$

where, $C$ is known as Curie constant.

Magnetic Permeability : magnetic field exists in vacuum. It can exist in other materials also. Magnetic permeability of a medium is defined as the ratio of magnetic intensity and the magnetising field,

$$ \text { i.e., } \quad \mu=\frac{B}{H} $$

Magnetic permeability of a material decides the ability of the material to allow magnetic lines of force through it.

Electromagnets and factors affecting their strengths

• Electromagnet is also known as a solenoid having a core of iron with wire wrapped around on it.

Factors which affect the strength of electromagnets are :

• nature of core material
• strength of current passing through the core
• number of turns of wire on the core
• shape and size of the core

Core is a solenoid having copper wire wound on it. More will be the number of turns, more will be the strength of magnetic field.

Permanent magnets

Magnets where magnetic field is generated by internal structure of material itself.

Permanent magnets have consistent non-varying magnetiefield having north and south pole linked with it.

Magnetic fields of permanent magnets are the sum of nuclear spins, electron spins and orbits of electrons.

Permanent magnets produce a longitudinal magnétic field between the poles.

Know the Terms

• Magnetic lines of force : The lines that are mapped out around the magnet.

Permanent magnet : A material, or piece of such material, which retains its magnetism even when not subjected to any external magnetic fields.

• Electromagnet: A magnet which aftracts metals only when electrically activated.

D Hysteresis : The intensity magnetisation $(M)$ or magnetic induction $(B)$ of the ferromagnetic substances lags behind the magnetising field $H$. The phenomenon is called hysteresis.

Know the Formulae

where, $\theta$ is the angle between $\vec{M}$ and $\vec{B}$

$$ \begin{aligned} & >\quad \chi_{m}=\mu_{r}-1 \ & >\quad I \propto \frac{H}{T} \ & >\quad \mu=\frac{B}{H} \ & B=\mu_{0}(H+M) \ & =\mu_{0}\left(H+\chi_{m} H\right)=\mu_{0}\left(1+\chi_{m}\right) H \end{aligned} $$

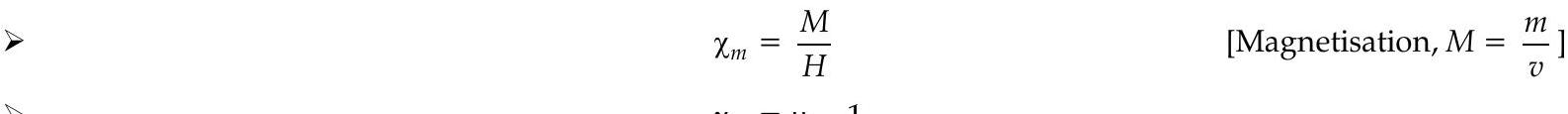
The force between two magnetic poles of strength $M=q_{m}$ and $m^{\prime}=q_{m}^{\prime}$ separated by a distance $r$ is given by

$$ \mathrm{F}=\frac{\mu_{0}}{4 \pi} \cdot \frac{q_{m} q_{m}^{\prime}}{r^{2}} $$

Factors affecting the strength of electromagnets

• Nature of core material.
• Strength of current passing through the core.
• Number of turns of wire on the core.
• Shape and size of the core.

Objective Answer Type Questions