SATHEE: electrostatic-potential-and-capacitance Question 51

electrostatic-potential-and-capacitance Question 51

Question: Q. 1. (i) Define the capacitance of a capacitor. Obtain the expression for the capacitance of a parallel plate capacitor in vacuum in terms of plate area $A$ and separation $d$ between the plates.

(ii) A slab of material of dielectric constant the same area as the plates of a parallel plate capacitor but has a thickness $\frac{2 d}{4}$ . Findthe fatio of the capacitance with dielectrie inside it to its capacitance without the dielectric.

U] [Foreign I, II, III 2017]

Show Answer

Solution:

Ans. (i) Definition of capacitance

(ii) Ratio of capacitances

(i) Capacitance equals the magnitude of the charge on each plate needed to raise the potential difference between the plates by unity.

(i) Try yourself, similar Q. 22 (i), Short Answer Type Question-II

(ii) Capacitance without dielectric,

$C = \frac{A ε_{0}}{d}$

Capacitance when filled with dielectric having thickness $\frac{3 d}{4}$

$\begin{aligned} C^{'} & = \frac{A ε_{0}}{(d - t + \frac{t}{κ})} 1 / 2 & = \frac{A ε_{0}}{(d - \frac{3 d}{4} + \frac{3 d}{4 κ})} [As t = \frac{3 d}{4}] \end{aligned}$

$\begin{aligned} = \frac{4 ε_{0} κ A}{d (κ + 3)} Ratio \frac{C^{'}}{C} & = \frac{A ε_{0} 4 κ}{d (κ + 3)} \times \frac{d}{A ε_{0}} & = \frac{4 κ}{(κ + 3)} \end{aligned}$

[CBSE Marking Scheme 2017]

[AI Q. 2. (i) Define the S.I. unit of capacitance.

(ii) Obtain expression for the capacitance of a parallel plate capacitor.

(iii) Derive the expression for the affective capacitance of a series combination of $n$ -capacitors.

R [Delhi Comptt. I, II, III, 2016]

Ans. (i) When a charge of one coulomb, produces a potential difference of one volt between the plates of a capacitor, the capacitance is one farad.

[Alternatively,

$Q = C V \Rightarrow C = \frac{Q}{V}$

When $Q = 1$ coulomb, $V = 1$ volt

$1 farad = \frac{1 coulomb}{1 volt}$

(ii) Try yourself, Similar to Q. 22 (i), Short Answer Type Question-II

(iii)

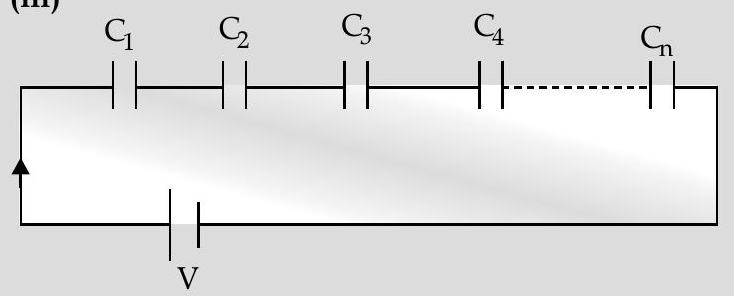
In series combination, charge on each capacitor is same.

Let it be $Q$ ,

$\begin{aligned} V_{1} = \frac{Q}{C_{1}} & V_{2} = \frac{Q}{C_{2}} & V_{n} = \frac{Q}{C_{n}} \end{aligned}$

Total potential

$\begin{aligned} V & = V_{1} + V_{2} + V_{3} + \dots + V_{n} V & = \frac{Q}{C_{1}} + \frac{Q}{C_{2}} + \frac{Q}{C_{3}} + \dots + \frac{Q}{C_{n}} \frac{V}{Q} & = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} + \dots + \frac{1}{C_{n}} \Rightarrow \frac{1}{C} & = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} + \dots + \frac{1}{C_{n}} \end{aligned}$

[CBSE Marking Scheme 2016]

Electrostatic Potential And Capacitance

electrostatic-potential-and-capacitance Question 51

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Electrostatic Potential And Capacitance

electrostatic-potential-and-capacitance Question 51

Table of Contents

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu