electrostatic-potential-and-capacitance Question 43
Question: Q. 17. Two capacitors of unknown capacitances $C_{1}$ and $C_{2}$ are connected first in series and then in parallel across a battery of $100 \mathrm{~V}$. If the energy stored in the two combinations is $0.045 \mathrm{~J}$ and $0.25 \mathrm{~J}$ respectively, determine the value of $C_{1}$ and $C_{2}$. Also calculate the charge on each capacitor in paraller combination.
A. Delhi I, II, III 2015]
Show Answer
Solution:
Ans. Energy stored in a capacitor
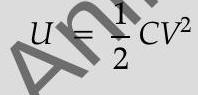
In series combination
$$ \begin{equation*} 0.045=\frac{1}{2} \frac{C_{1} C_{2}}{C_{1}+C_{2}}(100)^{2} \tag{i} \end{equation*} $$
$\Rightarrow \quad \frac{C_{1} C_{2}}{C_{1}+C_{2}}=0.09 \times 10^{-4}$
In parallel combination
$$ \begin{equation*} 0.25=\frac{1}{2}\left(C_{1}+C_{2}\right)(100)^{2} \tag{ii} \end{equation*} $$
$\Rightarrow \quad C_{1}+C_{2}=0.5 \times 10^{-4}$
On simplifying (i) and (ii)
$$ \begin{align*} C_{1} C_{2} & =0.045 \times 10^{-8} \ \left(C_{1}-C_{2}\right)^{2} & =\left(C_{1}+C_{2}\right)^{2}-4 C_{1} C_{2} \ & =\left(0.5 \times 10^{-4}\right)^{2}-4 \times 0.045 \times 10^{-8} \ & =0.25 \times 10^{-8}-0.180 \times 10^{-8} \ \left(C_{1}-C_{2}\right)^{2} & =0.07 \times 10^{-8} \ \left(C_{1}-C_{2}\right) & =2.6 \times 10^{-5}=0.25 \times 10^{-4} \quad \ldots(\text { iii }) \tag{iii} \end{align*} $$
From (ii) and (iii) we have
$1 / 2$ Charges on capacitors $C_{1}$ and $C_{2}$ in parallel combination
$Q_{1}=\mathrm{C}{1} V=\left(0.38 \times 10^{-4} \times 100\right)=0.38 \times 10^{-2} \mathrm{C} \quad 1 / 2$ $Q{2}=C_{2} V=\left(0.12 \times 10^{-4} \times 100\right)=0.12 \times 10^{-2} \mathrm{C} \quad 1 / 2$ Alternatively,
and
$$ \begin{aligned} \mathrm{U} & =\frac{1}{2} C V^{2} \ 0.045 & =\frac{1}{2}\left(\frac{C_{1} C_{2}}{C_{1}+C_{2}}\right)(100)^{2} \ 0.25 & =\frac{1}{2}\left(C_{1}+C_{2}\right)(100)^{2} \end{aligned} $$
If the student is unable to calculate $C_{1}$ and $C_{2}$, award him/her full 2 marks.
Also if the student just writes
$Q_{1}=C_{1} V=C_{1}(100)$ and $Q_{2}=C_{2} V=C_{2}(100)$
award him/her one mark for this part of the question.
[CBSE Marking Scheme, 2015]
