electrostatic-potential-and-capacitance Question 25
Question: Q. 3. In the circuit shown in Figure, initially key $K_{1}$ is closed and key :
$K_{2}$ is open. Then $K_{1}$ is opened and $K_{2}$ is closed (order is important). [Take $Q_{1}^{\prime}$ and $Q_{2}^{\prime}$ as charges on $C_{1}$ and $C_{2}$ and $V_{1}$ and $V_{2}$ as voltage respectively.]
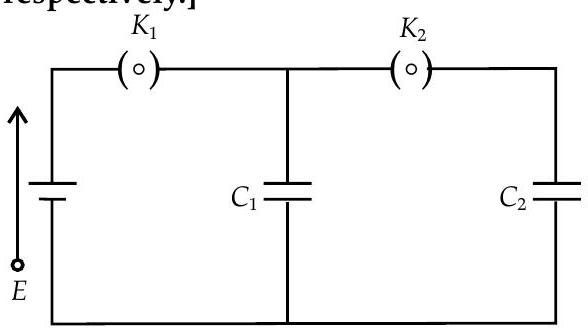
Then
(a) charge on $C_{1}$ gets redistributed such that $V_{1}=V_{2}$
(b) charge on $C_{1}$ gets redistributed such that $Q_{1}{ }^{\prime}=Q_{2}{ }^{\prime}$ (c) charge on $C_{1}$ gets redistributed such that $C_{1} V_{1}+$ $C_{2} V_{2}=C_{1} E$
(d) charge on $C_{1}$ gets redistributed such that $Q_{1}{ }^{\prime}+Q_{2}{ }^{\prime}$ $=Q$
[NCERT Exemp. Q. 2.11, Page 12]
Show Answer
Solution:
Ans. Correct options : (a) and (d)
Explanation: When key $k_{1}$ is closed and key $k_{2}$ is open, the capacitor $C_{1}$ is charged by cell and when $k_{1}$ is opened and $k_{2}$ is closed, the charge stored by capacitor $C_{1}$ gets redistributed between $C_{1}$ and $C_{2}$.
So, the charge on $C_{1}$ gets redistributed such that $Q_{1}{ }^{\prime}$ $+Q_{2}{ }^{\prime}=Q$
As $C_{1}$ and $C_{2}$ both are in parallel combination, so their potential will be equal, i.e., $V_{1}=V_{2}$. It verifies the answer (a).
