electrostatic-potential-and-capacitance Question 24
Question: Q. 2. A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness 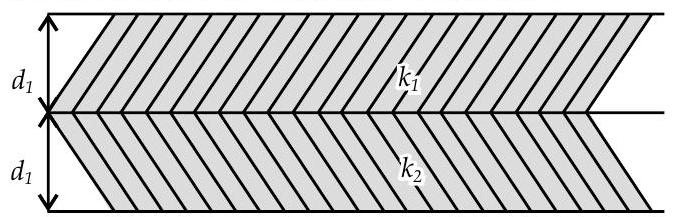$d_{1}$ and dielectric constant $\kappa_{1}$ and the other has thickness $d_{2}$ and dielectric constant $\kappa_{2}$ as shown in Figure. This arrangement can be thought as a dielectric slab of thickness $d\left(=d_{1}+d_{2}\right)$ and effective dielectric constant $\kappa$. The $\kappa$ is :
(a) $\frac{k_{1} d_{1}+k_{2} d_{2}}{d_{1}+d_{2}}$
(b) $\frac{k_{1} d_{1}+k_{2} d_{2}}{k_{1}+k_{2}}$
(c) $\frac{k_{1} k_{2}\left(d_{1}+d_{2}\right)}{\left(k_{1} d_{1}+k_{2} d_{2}\right)}$
(d) $\frac{2 k_{1} k_{2}}{k_{1}+k_{2}}$
[NCERT Exemplar]
Show Answer
Solution:
Ans. Correct option : (c)
Explanation: Capacitance of a parallel plate capacitor filled with dielectric of constant $k_{1}$ and thickness $d_{1}$ is,
$C_{1}=\frac{k_{1} \varepsilon_{0} A}{d_{1}}$
Similarly, for other capacitance of a parallel plate capacitor filled with dielectric of constant $k_{2}$ and thickness $d_{2}$ is,
$C_{2}=\frac{k_{2} \varepsilon_{0} A}{d_{2}}$
Both capacitors are in series so equivalent capacitance $\mathrm{C}$ is related as :
(2) $C_{1}+\frac{1}{C_{2}}=\frac{d_{1}}{k_{1} \varepsilon_{0} A}+\frac{d_{2}}{\mathrm{k}{2} \varepsilon{0} A}$
$$ \begin{equation*} =\frac{1}{\varepsilon_{0} A}\left[\frac{k_{2} d_{1}+k_{1} d_{2}}{k_{1} k_{2}}\right] \tag{i} \end{equation*} $$
So, $C=\frac{k_{1} k_{2} \varepsilon_{0} A}{\left(k_{1} d_{2}+k_{2} d_{1}\right)}$
$$ \begin{equation*} C^{\prime}=\frac{k \varepsilon_{0} A}{d} \tag{ii} \end{equation*} $$
where, $d=\left(d_{1}+d_{2}\right)$
So, multiply the numerator and denominator of eqn. (i) with $\left(d_{1}+d_{2}\right)$,
$$ \begin{equation*} C=\frac{k_{1} k_{2} \varepsilon_{0} A}{\left(k_{1} d_{2}+k_{2} d_{1}\right)} \cdot \frac{\left(d_{1}+d_{2}\right)}{\left(d_{1}+d_{2}\right)}=\frac{k_{1} k_{2}}{\left(k_{1} d_{2}+k_{2} d_{1}\right)} \cdot \frac{\varepsilon_{0} A}{\left(d_{1}+d_{2}\right)} . \tag{iii} \end{equation*} $$
Comparing eqns. (ii) and (iii), the dielectric constant of new capacitor is :
$k=\frac{k_{1} k_{2}\left(d_{1}+d_{2}\right)}{\left(k_{1} d_{2}+k_{2} d_{1}\right)}$
