Solution:

Ans. (i) Derivation of induced emf

$2 \frac{1}{2}$

(ii) Numerical

$2 \frac{1}{2}$

[CBSE Marking Scheme 2017]

Detailed Answer :

(i) $\times$

(ii)

$$ \begin{array}{rlrl} \omega & =360 \times \frac{2 \pi}{60}=12 \pi \mathrm{rad} / \mathrm{s} \quad 1 / 2 \ \varepsilon & =\frac{1}{2} B_{H} l^{2} \omega & 1 / 2 \ \therefore & 400 \times 10^{-3} & =\frac{1}{2} \cdot B_{H} \times\left(60 \times 10^{-2}\right)^{2} \times 12 \pi \frac{1}{1 / 2} \ \therefore & B_{H} & =\frac{5}{27 \pi}=0.06 \mathrm{~T} \end{array} $$

No change in emf if no. of spokes is increased. $1 / 2$

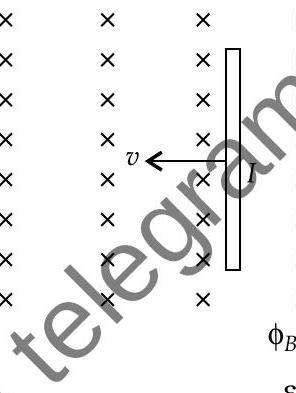
[AI Q. 3. (i) State Lenz’s law. Use it to predict the polarity of the capacitor in the situation given below :

R [O.D. I, II, III 2014]

(ii) A jet plane is travelling towards west at a speed of $1800 \mathrm{~km} / \mathrm{h}$.

(a) Estimate voltage difference developed between the ends of the wing having a span of $25 \mathrm{~m}$ if the earth’s magnetic field at the location has a magnitude of $5 \times 10^{-4} \mathrm{~T}$ and dip angle is $30^{\circ}$.

(b) How will the voltage developed be affected if the jet changes its direction from west to north?

[O.D. I, II, III 2015]

Ans. (i) Try Yourself, Similar Q. 4 of SAT questions-I $1 / 2$ In the above situation, north pole is approaching the magnet, so induced current in the face of the loop seen from left side will flow in such a way that it will behave like north pole, hence south pole gets developed in the loop as seen from right hand side of the loop. In such case the flow of induced current is clockwise, so A has positive polarity while $B$ has negative polarity.

(ii) (a)

$$ V=\mathrm{B} l v \quad 1 / 2+1 / 2 $$

Here, $B=$ vertical component of Earth’s magnetic field

$$ \begin{align*} B & =\left(5 \times 10^{-4} \sin 30^{\circ}\right) \mathrm{T} \ & =2.5 \times 10^{-4} \mathrm{~T} \ V & =\left[2.5 \times 10^{-4} \times 25 \times \frac{1}{1}\right. \ & =3.125 \mathrm{~V} \end{align*} $$

$$ \therefore \quad V=\left[2.5 \times 10^{-4} \times 25 \times \frac{1800 \times 10^{3}}{60 \times 60}\right] \mathrm{V} \quad 1 / 2 $$

(b) Now $B^{\prime}=$ horizontal component of Earth’s magnetic field

$$ \begin{aligned} \mathrm{B}^{\prime} & =B \cos 30^{\circ}=\frac{\mathrm{B} \sqrt{3}}{2} \ V^{\prime} & =B^{\prime} l V \ \therefore \quad V^{\prime} & =\sqrt{3} V=1.732 \times 3.125 \mathrm{volt}^{\star} \ & \cong 5.4 \mathrm{volt} \end{aligned} $$

[AI Q. 4. State the law which relates to generation of induced emf in a conductor being moved in a magnetic field.

Apply this law to obtain an expression for the induced emf when one ‘rod’ of a rectangular conductor is free to move in a uniform, time independent and ’normal’ magnetic field.

Apply the concept of the Lorentz (magnetic) force acting on a moving charge to justify the expression obtained.

R A [CBSE SQP 2014]

Ans. Faraday’s law of electromagnetic induction : It states that the induced emf is equal to the rate of change of magnetic flux.

In region $P Q R S$ as shown in figure, a uniform magnetic field $B$ which is perpendicular to the plane of paper is directed outwards as shown by dotted lines. In this, a rectangular loop of wire KLMN is held partially in magnetic field inside the plane of paper with $K L=l$. If $x$ is the portion on the loop inside the field at instant $t$, then on moving loop with velocity $v$ in plane of paper, the loop area linked with magnetic field changes. With this, an induced emf is set up in the wire which is observed through deflection in galvanometer $G$ which is connected in the loop.

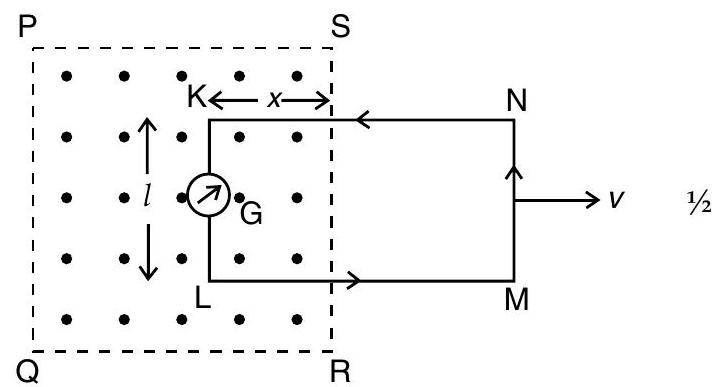
To calculate the emf induced, suppose in a small time $\Delta t$, the loop is moved out of magnetic field through a small distance $\Delta x$.

$\therefore$ Decrease in area of the loop

$$ =-l \Delta x $$

Decrease in magnetioflux linked with the loop

As induced emf, $\begin{aligned} d \phi & =-B l \Delta x \ \varepsilon & =-d \phi / d t\end{aligned}$

$\therefore \quad \varepsilon=\frac{B l \Delta x}{\Delta t}=B l v$

$1 / 2$

$\varepsilon=B l v$

$1 / 2$

We see that it is possible to show the motional emf expression using Lorentz force that acts on the free charge carriers of conductor $K L$. If an arbitrary charge $q$ inside conductor $K L$, moves with speed $v$ in magnetic field $B$, then as per Lorentz force, the charge will be $q v B$ in magnitude on. Here all charges will have similar force resulting in magnitude and direction irrespective of their position in rod $K L$.

The work done in moving the charge from $K$ to $L$ is, $\quad W=q v B \times l$

Since emf is the work done per unit charge,

$$ \begin{aligned} & \varepsilon=\frac{W}{q} \ & \varepsilon=B l v \end{aligned} $$

This equation gives emf induced across the rod KL.