Solution:

Ans. Derivation of expression for electric field 2 Proving that there is no electric field between plates

1

$$ \begin{aligned} & \text { By Gauss’s law } \oint \vec{E} \cdot \vec{d} s=\frac{q}{\varepsilon_{0}} \ & \therefore \quad 2 E A=\frac{\sigma A}{\varepsilon_{0}} \ & \therefore \quad E=\frac{\sigma}{2 \varepsilon_{0}} \ & \text { or } \quad \vec{E}=\frac{\sigma}{2 \varepsilon_{0}} A \end{aligned} $$

$1 / 2$

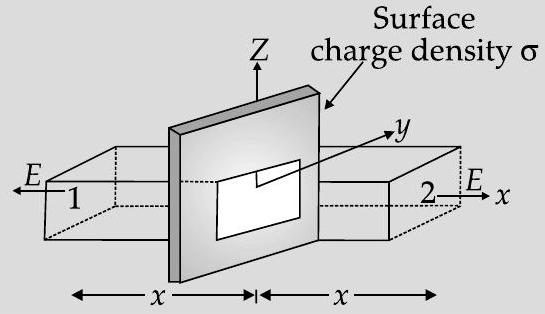
Electric field between two identical charged sheets

$\because$ Both the sheets have same charge density, their electric fields will be equal and opposite in the region between the two sheets.

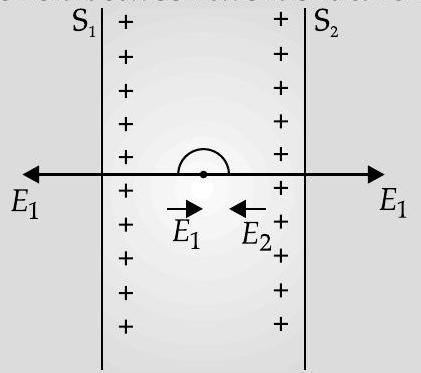
Hence the net field is zero.

[CBSE Marking Scheme, 2017]

Detailed Answer :

In the figure, if $\sigma$ is uniform surface charge density of an infinite plane sheet with $x$-axis to be normal to the plane, then by symmetry, electric field will not depend on $y$ and $z$ coordinates and their directions. Considering Gaussian rectangular parahlepiped surface with cross-sectional area $A$, two faces 1 and 2 will contribute to flux there electric field lines result as parallel to other faces which do not contribute to total flux.

It is analysed that unit vector which is normal to first surface will be in negative $x$ direction while unit vector which is normal to second surface will be in positive $+x$ direction, so flux E. $\Delta S$ by the surfaces will results equal and will add up.

Hence,

net flux through Gaussian surface $=2 \mathrm{EA}$

charge enclosed by closed surface $=\sigma \mathrm{A}$

As per Gauss’s law,

$$ \begin{aligned} & \oint \vec{E} \cdot \overrightarrow{d s}=\frac{q}{\varepsilon_{0}} \ & \therefore \quad 2 E A=\frac{\sigma A}{\varepsilon_{0}} \ & \text { Or, } \quad E=\frac{\sigma}{2 \varepsilon_{0}} \end{aligned} $$

This shows that the electric field around an infinite plane of charge does not vary with distance from the plane.

In terms of vector,

$$ \vec{E}=\frac{\sigma}{2 \varepsilon_{0}} \hat{n} $$

where,

$\hat{n}=$ unit vector normal to plane and going away from it

$\vec{E}=$ directed away from plate if $\sigma$ is (+) positive and toward the plate if $\sigma$ is (-) negative.

Since the two charged infinite plates have identical charges, so electric field between two identical charged sheets will be as shown in figure :

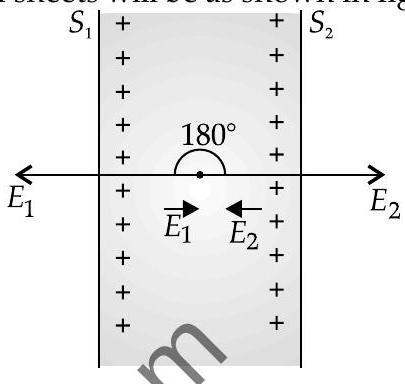
Now electric field due to surface 1

$$ \vec{E}{1}=\frac{\sigma}{2 \varepsilon{0}} $$

Now electric field due to surface 2

$$ \vec{E}{2}=-\frac{\sigma}{2 \varepsilon{0}} $$

Now the resultant electric field between the uniformly charged infinite plates $=\vec{E}{1}+\vec{E}{2}, \theta=180^{\circ}$

So,

$$ \begin{aligned} E & =\sqrt{E_{1}^{2}+E_{2}^{2}+2 E_{1} E_{2} \cos \theta} \ & =E_{1}-E_{2} \ & =\frac{\sigma}{2 \varepsilon_{0}}-\frac{\sigma}{2 \varepsilon_{0}}=0 \end{aligned} $$