electric-charges-and-fields Question 18
Question: Q. 8. Two point charges $q_{1}$ and $q_{2}$ are located at points $(a, 0,0)$ and $(0, b, 0)$ respectively. Find the electric field due to both these charges at the point $(0,0, c)$.
A [CBSE SQP 2013]
Show Answer
Solution:
Ans. We have $\overrightarrow{E_{\text {net }}}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}$
$$ =\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}}{r_{1}^{3}} \overrightarrow{r_{1}}+\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{2}}{r_{2}^{3}} \overrightarrow{r_{2}} $$
[AI Q. 1. (i) Derive the expression for electric field at a point on the equatorialline of an electric dipole.
(ii) Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
A [Delhi I 2017]
Ans. Derivation of expression of electric field on equatorial line of electric dipole Depiction of orientation for stable and unstable equilibrium in electric field $1 / 2+1 / 2$
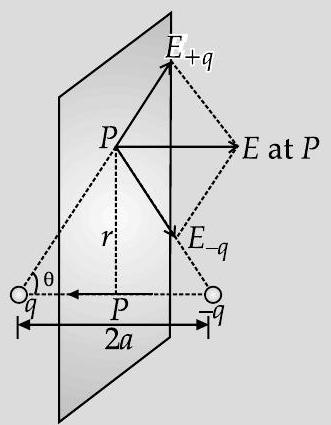
(i) Let the point ’ $P$ ’ be at a distance ’ $r$ ’ from the mid point of the dipole. where, $\overrightarrow{r_{1}}=-a \hat{i}+c \hat{k}$
and $\quad \overrightarrow{r_{2}}=-b \hat{j}+c \hat{k}$
$$ \overrightarrow{E_{n e t}}=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q_{1}(-a \hat{i}+c \hat{k})}{\left(a^{2}+c^{2}\right)^{3 / 2}}+\frac{q_{2}(-b \hat{j}+c \hat{k})}{\left(b^{2}+c^{2}\right)^{3 / 2}}\right] \mathbf{1} $$
[CBSE Marking Scheme, 2013]
