current-electricity Question 43
Question: Q. 1. State Kirchhoff’s laws of current distribution in an electrical network.
Using these rules determine the value of the current $I_{1}$ in the electric circuit given below :
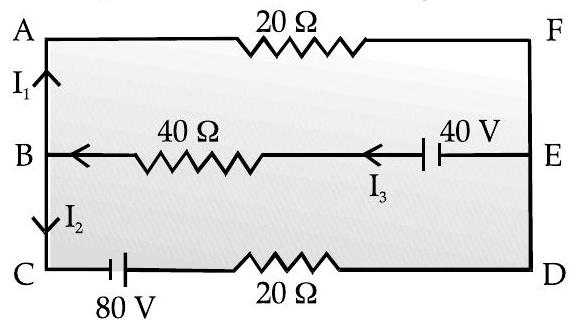
R&A [Delhi I, II, III 2014]
Show Answer
Solution:
Ans. (i) Kirchhoff’s laws 1
(ii) Finding value of current $I_{1}$ in electric circuit 2
[CBSE Marking Scheme 2014]
Detailed Answer :
(i) Try yourself Similar to Q. 1, Short Answer Type Question-I
(ii) Now from the given figure,
$$ \begin{aligned} I_{1}+I_{2} & =I_{3} \ I_{2} & =I_{3}-I_{1} \end{aligned} $$
For $A B E F A$
$$ \begin{align*} -20 I_{1}-40 I_{3} & =-40 \ -20\left(I_{1}+2 I_{3}\right) & =-40 \ I_{1}+2 I_{3} & =2 \tag{iii} \end{align*} $$
For $B C D E B$
$$ \begin{array}{rlr} 40 I_{3}+20 I_{2} & =80+40 \ 20\left(2 I_{3}+I_{2}\right) & =120 \ 2 I_{3}+I_{2} & =6 \ 2 I_{3}+\left(I_{3}-I_{1}\right) & =6 & \ 2 I_{3}+I_{3}-I_{1} & =6 & \ 3 I_{3}-I_{1} & =6 & \text { using eq. (i) } \tag{iv} \end{array} $$
Now solving eqns. (iii) and (iv),
We get
$$ I_{3}=\frac{8}{5}=1.6 \mathrm{~A} $$
and
$$ I_{1}=-\frac{6}{5} \mathrm{~A}=-1 \cdot 2 \mathrm{~A} $$
Now, from equation (ii),
$$ \begin{array}{rlrl} & & I_{2} & =I_{3}-I_{1} \ \Rightarrow & & =1.6-(-1.2) \ \Rightarrow & & =1.6+1.2 \ \Rightarrow & & =2.8 \mathrm{~A} \end{array} $$
[AI Q. 2. Using Kirchhoff’s rules, calculate the potential difference between $B$ and $D$ in the circuit diagram as shown in the figure.
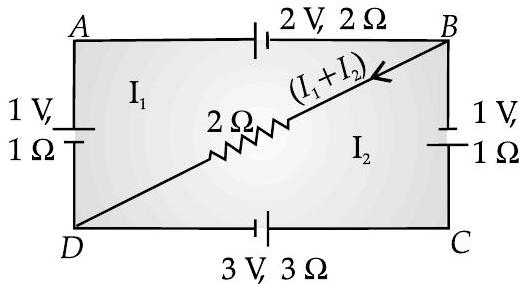
A [CBSE-2018 Comptt.]
Sol. Writing the two loop equations
$1 / 2+1 / 2$
Finding the current through DB
Finding the p.d. between B and D
Using Kirchhoff’s voltage rule, we have :
For loop $D A B D$
$\left(1 \times I_{1}+(1)+(-2)+2 I_{1}+2\left(I_{1}+I_{2}\right)=0\right.$
Or $5 I_{1}+2 I_{2}=1$
..(i) $1 / 2$
For loopDCBD
$+I_{2} \times 3+(3)+(-1)+1 \times I_{2}+2\left(I_{1}+I_{2}\right)=0$
Or $\left.2 I_{1}\right)+6 I_{2}=-2$
…(ii) $1 / 2$
Solving (i) and (ii), we get
$$ \begin{aligned} & I_{1}=\frac{5}{13} \mathrm{~A} \ & I_{2}=\frac{-6}{13} \mathrm{~A} \end{aligned} $$
$\therefore$ Current through $D B=I_{1}+I_{2}=\frac{-1}{13} \mathrm{~A}$
$1 / 2$
$\therefore$ P.D. between $B$ and $D=0.154 \mathrm{~A}$
[CBSE Marking Scheme 2018]
