current-electricity Question 40
Question: Q. 3. (i) Define the term ‘drift velocity’ of charge carriers in a conductor. Obtain the expression for the current density in terms of relaxation time.
(ii) A
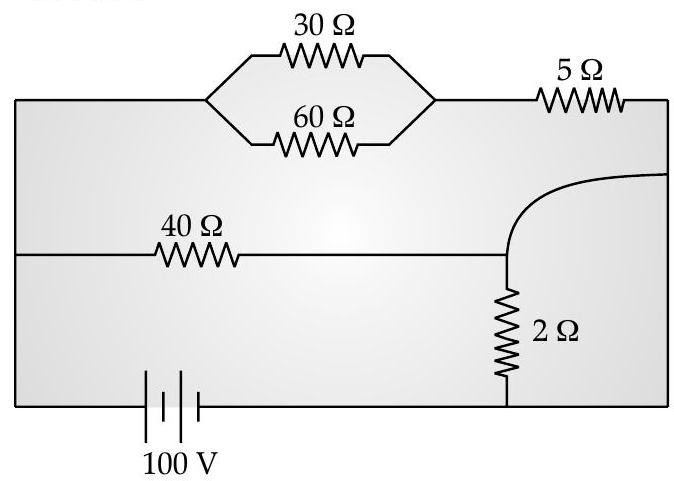
R A [O.D. I, II, III, 2013; Foreign, 2014]
Show Answer
Solution:
Ans. (i) Try yourself Similar to Q. 1 (i) Long answer Type Questions.
(ii) Current flowing through the resistance
Current through
[CBSE Marking Scheme 2014]
[AI Q. 4. (i) Why do the ‘free electrons’, in a metal wire, ‘flowing by themselves’, not cause any current flow in the wire?
Define ‘drift velocity’ and obtain an expression for the current flowing in a wire, in terms of the ‘drift velocity’ of the free electrons.
(ii) Use the above expression to show that the ‘resistivity’, of the material of a wire, is inversely proportional to the ‘relaxation time’ for the ‘free electrons’ in the metal. R&U [Foreign Comptt. 2016]
Ans. (i) The free electrons, in a metal, (flowing by themselves), have a random distribution of their velocities. Hence the net charge crossing any cross section, in unit time, is zero.
The ‘drift velocity’ equals the average (time’ dependant) velocity acquired by free electrons, under the action of an applied (external) electric field.
We have, for an applied electric field
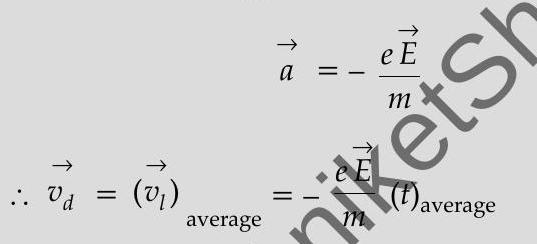
The average time, between successive collisions, is called the ‘Relaxation time’ and is denoted by
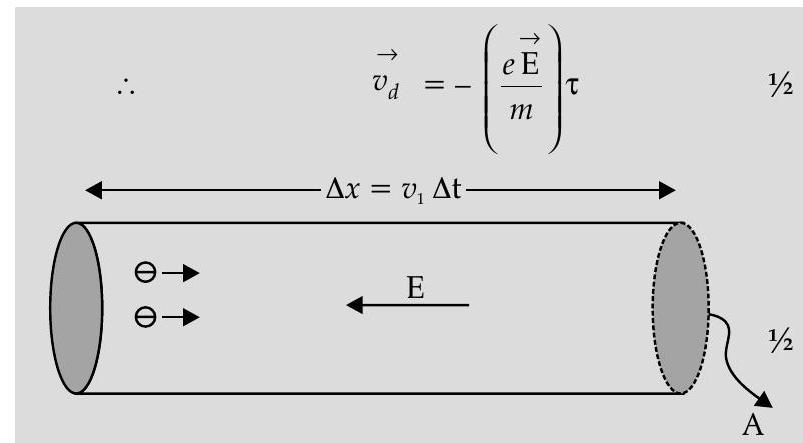
Because of the drift, we can write
But
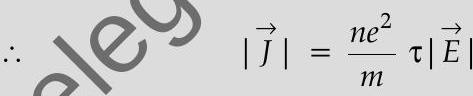
But
Also we can write,
(ii) We have
[CBSE Marking Scheme 2016]
TOPIC-2
Kirchhoff’s Laws, Wheatstone Bridge and their Applications
Revision Notes
Kirchhoff’s Laws
Kirchhoff’s Laws tell about the relationship between voltages and currents in circuits.
First Law
Kirchhoff’s first law is also known as junction law which states that for a given junction or node in a circuit, sum of the currents entering in a junction will be equal to sum of currents leaving that junction.
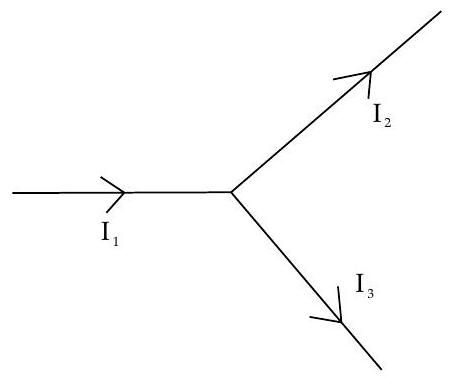
OR
The algebric sum of all currents meeting at a junction in a closed circuit is zero. i.e.,
This is called the law of conservation of charge.
Second Law
Kirchhoff’s second law is also known as loop law which shows that around any closed loop in a circuit, sum of the potential differences across all elements will be zero. i.e.,
This is called the law of conservation of energy.
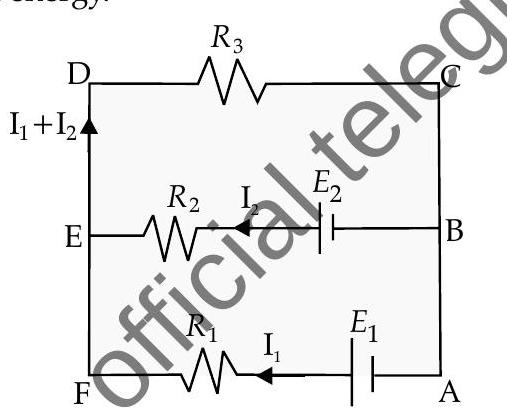
For example : Applying Junction law in loge AFÉBA
Wheatstone Bridge
It is a circuit having four resistances
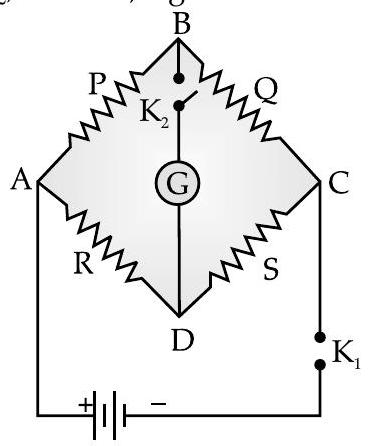
Wheatstone Bridge
It is a balanced bridge when there is no current through the galvanometer and potential at node
D Conductance : The reciprocal of resistance with unit as siemens, “S.”
Node : An end point to any branch of a network or a junction common to two or more branches.
P Permittivity: The ratio of capacitance between two electrodes with dielectric to capacitance with air between the electrodes.
Galvanometer : An instrument for detecting and measuring small electric currents.
Know the Formulae
Kirchhoff’s Law (junction law)
Kirchhoff’s Law (Loop law)
Wheatstone Bridge






