current-electricity Question 36
Question: Q. 14. A student connects a cell, of emf $E_{2}$ and internal resistance $r_{2}$ with a cell of emf $E_{1}$ and internal resistance $r_{1}$, such that their combination has a net internal resistance less than $r_{1}$. This combination is then connected across a resistance $R$.
Draw a diagram of the ‘set-up’ and obtain an expression for the current flowing through the resistance.
R [Foreign Comptt., 2016]
Show Answer
Solution:
Ans. Since $r_{e q}<r_{1}$, the two cells must have been connected in parallel.
The diagram of the setup is as shown
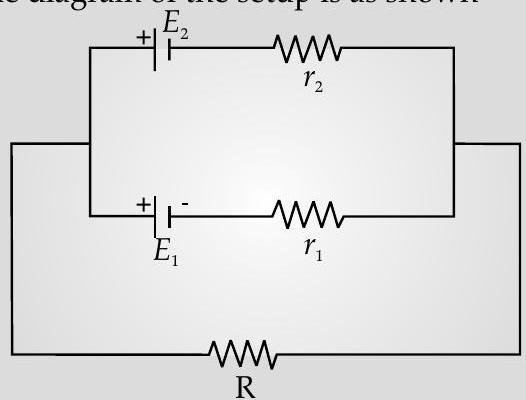
Note :
[Award $(1 / 2+1 / 2+=1)$ mark even if the student directly draws the diagram of the setup]
Equivalent internal resistance, $r=\frac{r_{1} r_{2}}{\left(r_{1}+r_{2}\right)}$
$1 / 2$
Equivalent emf, $E$ is given by
$$ E=\left(\frac{E_{1}}{r_{1}}+\frac{E_{2}}{r_{2}}\right) r $$
The current, flowing through $R$, is
$$ I=\frac{E}{(R+r)} $$
where, $E$ and $r$ are given by the above expressions. $1 / 2$ [Note : Award 2 marks if the student obtains / writes the expression, $I=\frac{E_{1} r_{2}+E_{2} r_{1}}{\left[R\left(r_{1}+r_{2}\right)+r_{1} r_{2}\right]}$ for the current flowing through $R]$.
[CBSE Marking Scheme, 2016]
